こんにちは(@t_kun_kamakiri)。
前回の記事では、「2次元のラプラス方程式」をGoogle Colab上でPythonで実装しました。
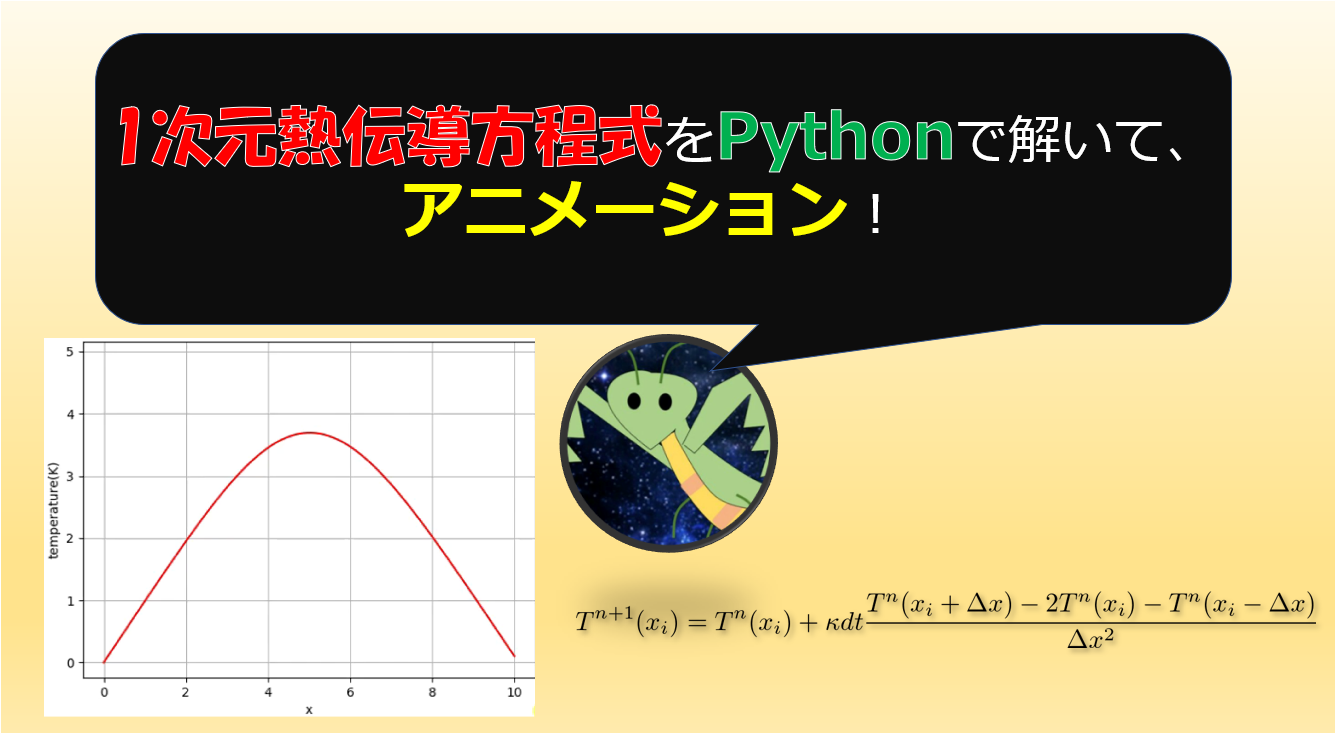
今回は、以下のような２次元のポアソン方程式をPythonで実装します。
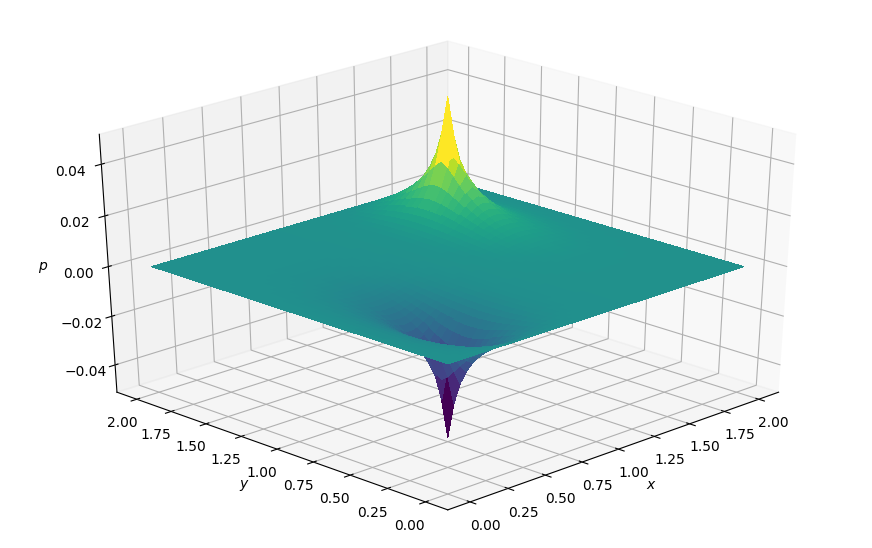
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
２次元のポアソン方程式の数値計算をPythonで実装
ポアソン方程式
まずは、
- ポアソン方程式がどういう式なのか
- ナビエストークス方程式のを解く際のポアソン方程式の使われ方
を復習しておきましょう。
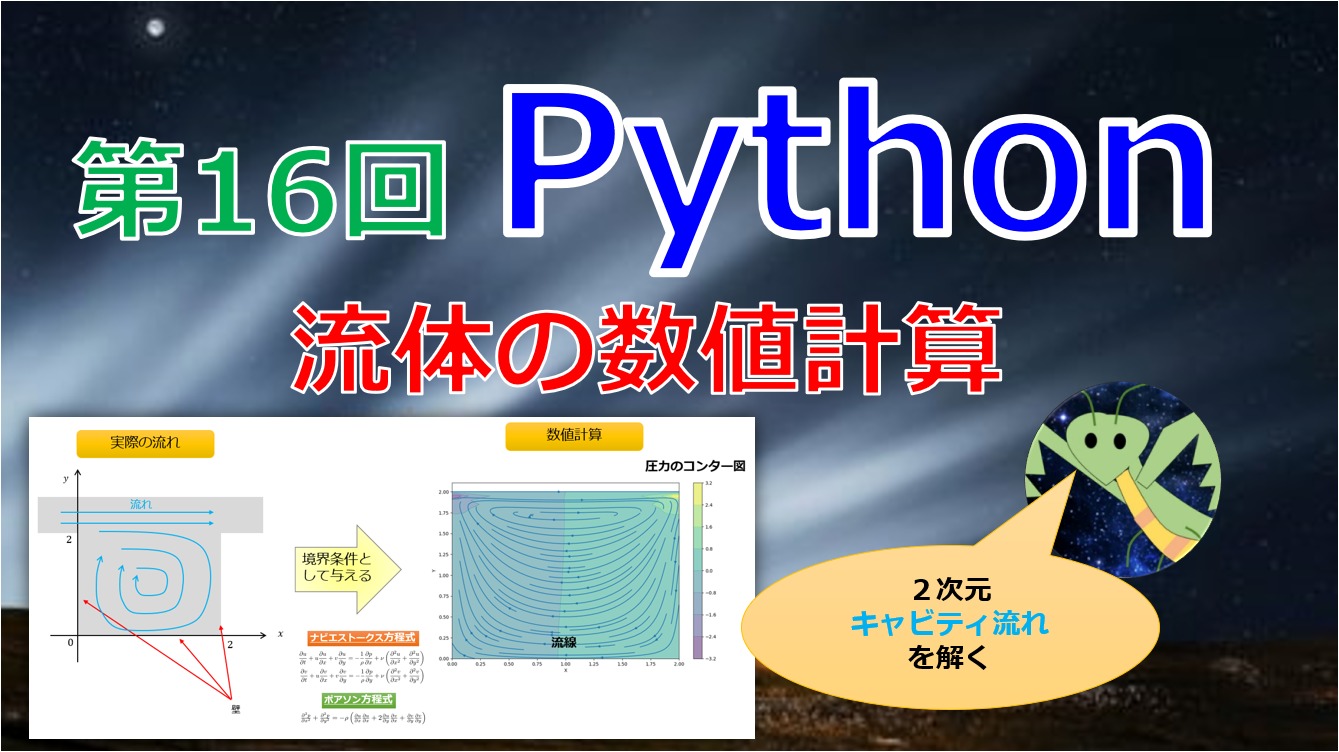
流体現象を扱う際に「ナビエストークス方程式」と「質量保存則」を連立して解く必要があります。
ナビエストークス方程式
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{1}
\end{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right) \tag{2}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = b(x,y)\tag{3.1}
\end{align*}
b(x,y)=-\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{3.2}
\end{align*}
\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = 0
\end{align*}
\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = b(x,y)
\end{align*}
\frac{\partial ^2 \phi}{\partial x^2} + \frac{\partial ^2 \phi}{\partial y^2} = -\frac{\rho(\boldsymbol{r})}{\epsilon}
\end{align*}
ポアソン方程式を離散化
ポアソン方程式は偏微分の方程式なので、離散化して代数的に取り扱えるようにしないと数値計算ができません。
\frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n}-2 p_{i,j}^{n}+p_{i,j-1}^{n}}{\Delta y^2}=b_{i,j}^{n}\tag{4}
\end{align*}
p_{i,j}^{n}=\frac{(p_{i+1,j}^{n}+p_{i-1,j}^{n})\Delta y^2+(p_{i,j+1}^{n}+p_{i,j-1}^{n})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}\tag{5}
\end{align*}
p_{i,j}^{n}=\frac{p_{i+1,j}^{n}+p_{i-1,j}^{n}+p_{i,j+1}^{n}+p_{i,j-1}^{n}-b_{i,j}^{n}\Delta x^2}{4}\tag{6}
\end{align*}
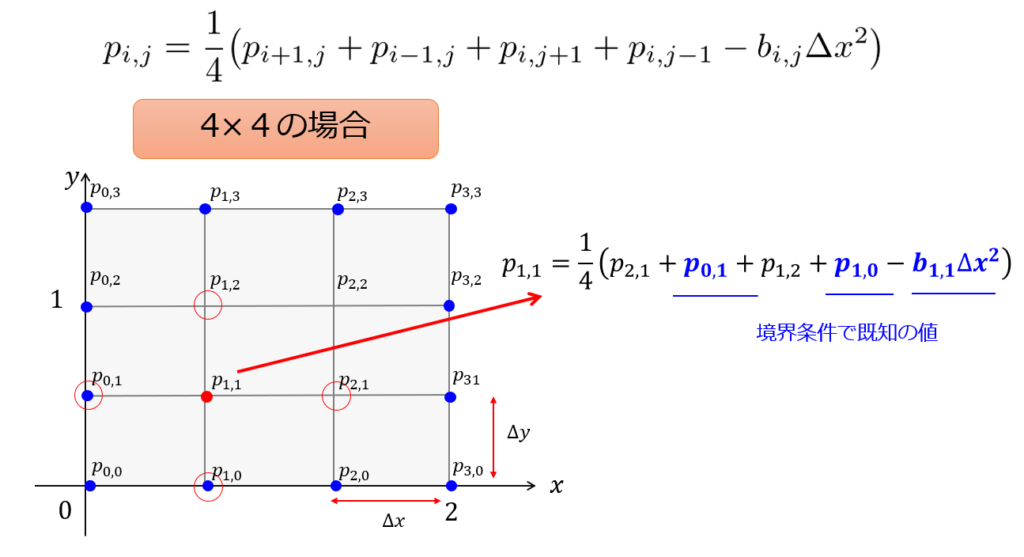青文字は境界条件で値が与えられているので、既知の値です。これを見ればわかるように、(i,j)の格子点での圧力はその周りの圧力の平均値として計算しています。
境界条件を設定
ポアソン方程式は、時間発展の方程式ではなく、境界条件によって空間分布の解が与えられる方程式なので、境界条件を設定する必要があります。
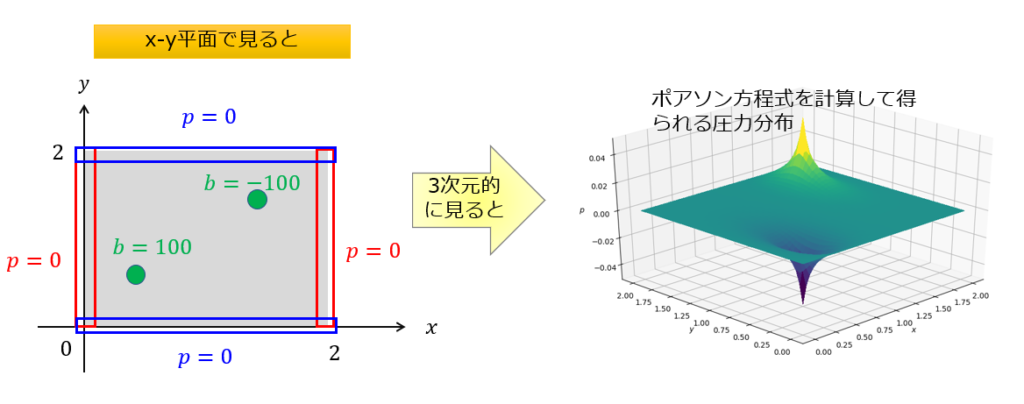
今回与える境界条件は以下のようにします。
- \(x=0, 2\)：\(p=0\)
- \(y=0, 1\)：\(p=0\)
- \(i=\frac{1}{4}nx, j=\frac{1}{4}ny\)：\(b_{i,j}=100\)
- \(i=\frac{3}{4}nx, j=\frac{3}{4}ny\)：\(b_{i,j}=-100\)
ちょっとわかりにくいかもしれないので、絵にしてみました。
ポアソン方程式をPythonで実装
【ポイント】
- 必要なライブラリをインポートする。
コードを以下のように書きます。
1 2 3 4 | import numpy as np from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D |
NumpyとMatplotlibをインポートします。
記述ミスがなければエラーなく進みます。
【ポイント】
- 初期状態を設定
- 境界条件を設定
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | # 条件設定 nx = 50 ny = 50 nt = 100 xmin = 0 xmax = 2 ymin = 0 ymax = 1 dx = (xmax - xmin) / (nx - 1) dy = (ymax - ymin) / (ny - 1) # 初期状態 p = np.zeros((ny, nx)) pd = np.zeros((ny, nx)) b = np.zeros((ny, nx)) x = np.linspace(xmin, xmax, nx) y = np.linspace(xmin, xmax, ny) # 点源 b[int(ny / 4), int(nx / 4)] = 100 b[int(3 * ny / 4), int(3 * nx / 4)] = -100 |
これで、初期状態の圧力のプロファイルができています。
初期状態と言っても、境界条件を課しただけですので初期の状態には何の意味もありません。
あくまで境界条件をもとにラプラス方程式を解いて得られた圧力分布に意味があるので、初期状態はその最終状態を得るための種を与えているにすぎません。
【ポイント】
p_{i,j}^{n}=\frac{p_{i+1,j}^{n}+p_{i-1,j}^{n}+p_{i,j+1}^{n}+p_{i,j-1}^{n}-b_{i,j}^{n}\Delta x^2}{4}\tag{6}
\end{align*}
コードを以下のように書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 | for it in range(nt): pd = p.copy() p[1:-1,1:-1] = (((pd[1:-1, 2:] + pd[1:-1, :-2]) * dy**2 + (pd[2:, 1:-1] + pd[:-2, 1:-1]) * dx**2 - b[1:-1, 1:-1] * dx**2 * dy**2) / (2 * (dx**2 + dy**2))) p[0, :] = 0 p[ny-1, :] = 0 p[:, 0] = 0 p[:, nx-1] = 0 |
これで最終状態の圧力の分布が計算されました。
前回のラプラス方程式を解いた際には、全ての格子点上の値の合計と前のステップでの値の合計とを比較して、「1e-4（0.01%)」以下の誤差になれば収束したと判定していましたが、今回は収束条件を反復回数（100回）にしています。
※反復計算には「ヤコビ法」と呼ばれる方法で計算しています。
では、次に収束した圧力分布を可視化してみてみましょう。
【ポイント】
コードを以下のように書きます。
1 2 3 4 5 6 7 | def plot2D(x, y, p): fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) ax.view_init(30, 225) ax.set_xlabel('$x |
これで、可視化するための関数が完成したので、以下のように関数を呼び出して圧力分布を可視化してみましょう。
1 | plot2D(x, y, p) |
【結果】
このようになればOKです(^^)/
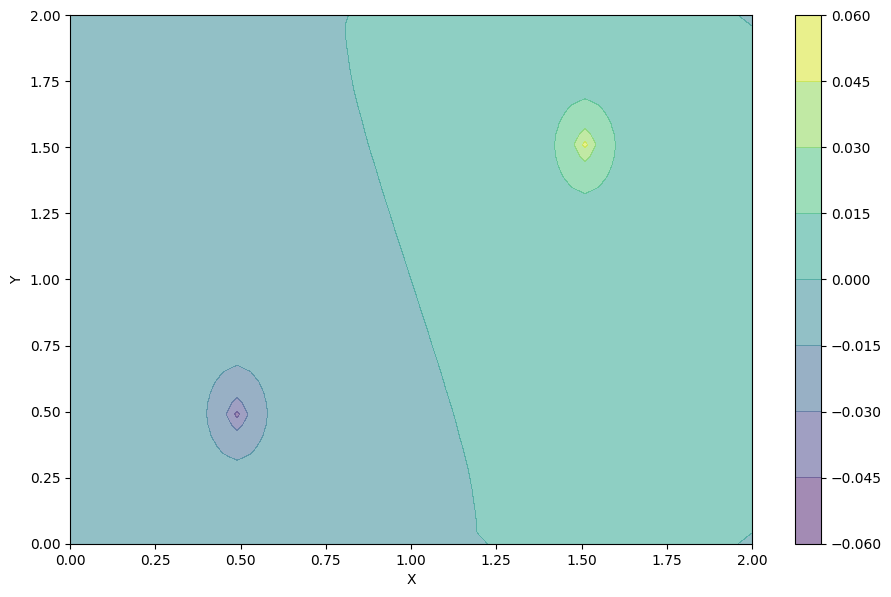
コンター図も作成してみる
Matplotlibの公式ドキュメントは非常にわかりやすい（たぶんPythonがわかりやすいから）ので、コンター図もサクッと作成できます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #オブジェクトを生成 fig = plt.figure(figsize=(11,7), dpi=100) fig xmin = 0 xmax = 2 ymin = 0 ymax = 2 x = np.linspace(xmin, xmax, nx) y = np.linspace(xmin, xmax, ny) X, Y = np.meshgrid(x, y) plt.contourf(X, Y, p, alpha=0.5, cmap=cm.viridis) plt.colorbar() plt.xlabel('X') plt.ylabel('Y') |
【結果】
このように圧力の分布もコンターで可視化できます。
まとめ
今回は、2次元のポアソン方程式をPythonで実装してみました。
本記事のシリーズを読むことでPythonを使ったナビエストークス方程式の実装まではいけると思いますので、是非最後までお付き合いくださいm(__)m
次回は、いよいよナビエストークス方程式をPythonで実装してみたいと思います(^^)/
おすすめの書籍紹介
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。
やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。
数値計算の書籍
今回紹介したポアソン方程式は「ヤコビ法」と呼ばれる反復計算を行っていますが、その他の有名な数値的解法のをいくつか挙げておきます。
- ガウス消去法（直接法）
- ガウス・ジョルダン法（直接法）
- ヤコビ法（反復法）
- ガウス・ザイデル法（反復法）
- SOR法（反復法）
などがあります。
詳しく勉強したい方は、以下の参考書がとてもわかりやすいです。
数値計算の闇について詳しく知りたい方は、☟こちらの参考書も合わせてお読みください。
ご質問に対する回答
ブログのコメントに「b[int(ny / 2), int(nx / 2)] = -10.e-8」の電荷として解けないかという質問がありましたので、全体のコードを載せておきます。
下記のコードをmain.pyに書き、python main.pyで実行すれば動作するかと思います。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | from matplotlib import pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D import numpy as np # 条件設定 nx = 50 ny = 50 nt = 100 xmin = 0 xmax = 2 ymin = 0 ymax = 1 dx = (xmax - xmin) / (nx - 1) dy = (ymax - ymin) / (ny - 1) # 初期状態 p = np.zeros((ny, nx)) pd = np.zeros((ny, nx)) b = np.zeros((ny, nx)) x = np.linspace(xmin, xmax, nx) y = np.linspace(xmin, xmax, ny) # 点源 b[int(ny / 2), int(nx / 2)] = -10.e-8 for it in range(nt): pd = p.copy() p[1:-1,1:-1] = (((pd[1:-1, 2:] + pd[1:-1, :-2]) * dy**2 + (pd[2:, 1:-1] + pd[:-2, 1:-1]) * dx**2 - b[1:-1, 1:-1] * dx**2 * dy**2) / (2 * (dx**2 + dy**2))) p[0, :] = 0 p[ny-1, :] = 0 p[:, 0] = 0 p[:, nx-1] = 0 def plot2D(x, y, p): fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) ax.view_init(30, 225) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('p') plot2D(x, y, p) plt.show() |
![](<iframe style="border: none;" src="https://rcm-fe.amazon-adsystem.com/e/cm?o=9&p=13&l=ur1&category=audible&banner=07J5KH0DSN7BCRWR0F82&f=ifr&linkID=d1dd57270470731eb3c6d0054e4dffe8&t=korokoro00d-22&tracking_id=korokoro00d-22" width="468" height="60" frameborder="0" marginwidth="0" scrolling="no"></iframe>)
(5)式から(6)式への式変形のところで質問があります。
Δx=Δyとした場合、(6)式のb_(i,j)^nの部分は、b_(i,j)^nではなく、(b_(i,j)^n)(Δy)^2 or (b_(i,j)^n)(Δx)^2ではないのですか？
私の計算ミスでしたらごめんなさい。
よろしくお願いします。
ご指摘ありがとうございます。
おっしゃるとおりです。失礼致しました。
修正したいと思います。
数値計算の方は、修正の必要は無く正しいです。
ありがとうございました。
最近Pythonを使い始めとても参考になる内容をありがとうございます。
今回使ったコードを電位分布、電場分布を求める場合に真ん中に電荷があるときは点源のところをb[int(ny / 2), int(nx / 2)] = -10.e-8
で使えますか？
最近Pythonを触り始めとても参考になる内容をありがとうございます。
初心的な質問で申し訳ありませんが
このコードを真ん中に電荷がある領域の電位分布を求める時の点源のコードはb[int(ny / 2), int(nx / 2)] = -10.e-8だとうまくいきませんでしたがどう変えたらいいでしょうか
コメントいただきありがとうございます。
うまくいかないというのはエラーで計算ができないということでしょうか。
私の手元で以下のようなコードをmain.pyに書いて、python main.pyと実行するとポアソン方程式を解いてくれているように思えます。
一度お確かめください。なお、Pythonはインデントをつけないとエラーになるのでコピペする際には十分注意してください。
コードはブログの一番最後にも書きましたのでご確認お願い致します。
from matplotlib import pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# 条件設定
nx = 50
ny = 50
nt = 100
xmin = 0
xmax = 2
ymin = 0
ymax = 1
dx = (xmax – xmin) / (nx – 1)
dy = (ymax – ymin) / (ny – 1)
# 初期状態
p = np.zeros((ny, nx))
pd = np.zeros((ny, nx))
b = np.zeros((ny, nx))
x = np.linspace(xmin, xmax, nx)
y = np.linspace(xmin, xmax, ny)
# 点源
b[int(ny / 2), int(nx / 2)] = -10.e-8
for it in range(nt):
pd = p.copy()
p[1:-1,1:-1] = (((pd[1:-1, 2:] + pd[1:-1, :-2]) * dy**2 +
(pd[2:, 1:-1] + pd[:-2, 1:-1]) * dx**2 –
b[1:-1, 1:-1] * dx**2 * dy**2) /
(2 * (dx**2 + dy**2)))
p[0, :] = 0
p[ny-1, :] = 0
p[:, 0] = 0
p[:, nx-1] = 0
def plot2D(x, y, p):
fig = plt.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection=’3d’)
X, Y = np.meshgrid(x, y)
surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False)
ax.view_init(30, 225)
ax.set_xlabel(‘x’)
ax.set_ylabel(‘y’)
ax.set_zlabel(‘p’)
plot2D(x, y, p)
plt.show()
丁寧な回答ありがとうございます。とりあえず一つの点で電荷を置く場合は理解できましたが1ｍの領域の真ん中に10ｃｍの電荷を置く、などここからここまでの範囲に電荷を置く場合のコードがどうなるか分かりません。お時間があればご回答頂けないでしょうか？