こんにちは(@t_kun_kamakiri)。
本日は、「Pythonでスライスによる要素の参照」というのをやります。
これにより、メインプログラムでfor文で計算を回すよりも、計算速度が速くなるので計算時間も比較しながら解析をしたいと思います。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
- スライスの基本
- for文とスライスによる計算時間の計測の比較
前回の記事までで、「1次元の移流方程式」「1次元の拡散方程式」「1次元バーガース方程式」をPythonで実装するというのをやりましたが、今回はPythonでの計算速度を早くする方法のひとつであるスライスについて慣れておきたいと思います。
スライスの基本
スライスは、リスト型だけではなく文字列、タプルにも使うことができます。
スライスは「リスト」「文字列」「タプル」に使うことができる。
スライスに基本は例えば以下のように使います。
以下のようにリストを用意します。
1 2 3 | a = [0,1,2,3,4,5,6,7,8,9,10] a |
【結果】
1 | [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] |
普通のリストですね。
これをスライスを使って要素を抽出します。
それにはいくつか書き方があるのですが、基本的な書き方は[start:stop:step]です。
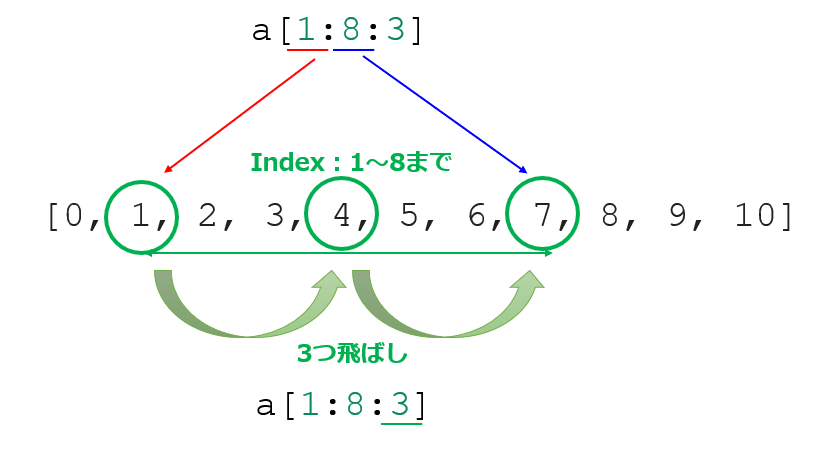
例えば以下のように書くと、
1 | a[1:8:3] |
【結果】
1 | [1, 4, 7] |
👆このようになります。
これは次のようになっていると理解してください。
すべての要素を取り出すときは以下のように書きます。
1 | a[:] |
【結果】
1 | [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] |
「Index:1~3」の値を抽出したい場合はstepを指定しなければ、stepは1となるので以下のよう書けばOKです。
1 | a[0:3] |
【結果】
1 | [0, 1, 2] |
また、次のように最後の2つ目まですべて抽出したい場合は、マイナスをつけることで抽出できます。
1 | a[:-2] |
【結果】
1 | [0, 1, 2, 3, 4, 5, 6, 7, 8] |
基本的にはこのようにスライスを使って要素を抽出ることができます。
本記事ではリスト型を主に近いNumPy配列オブジェクトのndarrayでのスライスを使った解説がメインになります。
Numpy配列でのスライスの例
まずは、以下のようなシンプルな例を考えてみましょう。
u^{n+1}_{i}=u^{n}_{i}-u^{n}_{i-1}\tag{1}
\end{align*}
\(u^{n}=[0,1,2,3,4,5]\)なので、これを(1)式に従って計算する場合、今までは以下のようにfor文を使って計算していましたよね。
1 2 3 4 5 6 | import numpy as np u = np.array((0, 1, 2, 3, 4, 5)) for i in range(1, len(u)): print(u[i] - u[i-1]) |
【結果】
1 2 3 4 5 | 1 1 1 1 1 |
これは毎回、uという配列の要素をひとつひとつ取り出して、 u[i] – u[i-1]という計算を行っているので時間がかかるんですよね。
しかし、スライスというのを使えば、一回のコマンドで同様の計算ができて、かつ計算時間が短くて済みます。
1 | u[1:] - u[0:-1] |
👆以上です。
これで先ほどのfor文と同じ結果になります。
これはndarray配列の場合は、各要素ごとに計算をすることになるので以下のように計算がされています。


for文を使った場合とスライスを使った場合の計算時間を計測
Pythonは上で見たようなスライスを使った方法の方が、for文を使うよりも計算が速くなります。
試しにfor文とスライスでの計算時間を計測して比較してみましょう。
コードの先頭に「%time」や「%%time」と書くことで、計算時間の計測してくれます。
- %time:1回の計算時間を算出
- %%time:何回か計算してその計算時間の平均を算出
では、まずはfor文から・・・
1 2 3 4 5 6 7 | %%timeit import numpy as np u = np.array((0, 1, 2, 3, 4, 5)) for i in range(1, len(u)): u[i] - u[i-1] |
【結果】
1 2 | The slowest run took 7.71 times longer than the fastest. This could mean that an intermediate result is being cached. 100000 loops, best of 3: 3.63 µs per loop |
100000回の中でベストは「3.63μs」という結果ですね。
では、次にスライスを使ったコードを見てみましょう。
1 2 3 4 5 6 7 | %%timeit import numpy as np u = np.array((0, 1, 2, 3, 4, 5)) u[1:] - u[0:-1] |
【結果】
1 2 | The slowest run took 15.39 times longer than the fastest. This could mean that an intermediate result is being cached. 100000 loops, best of 3: 2.42 µs per loop |
100000回の中でベストは「2.42μs」という結果ですね。
やはり、スライスを使った方が計算時間が速いという結果になりましたね。
このように、Pythonはインタプリタ型の言語であるためコンパイラによる最適化がなく、コードの書き方の工夫で計算時間が速くなります。
Numpy自体が数値計算のためのライブラリであるため計算速度向上に貢献しているわけですが、for文を使ったごり押しの計算よりスマートにスライスと使えば、記述方法も計算時間も速くなるというメリットがあります。
少し余談になりますが、for文でndarray配列を作るときは、できるだけappendは使わない方が計算が速かったりもします。
例えば以下の2つのコードは同じ結果になりますが、計算時間が違います。
例1)appendを使って要素を格納
1 2 3 4 5 6 7 8 | %%timeit import numpy as np du = [] u = np.array((0, 1, 2, 3, 4, 5)) for i in range(1, len(u)): du.append(u[i] - u[i-1]) |
【結果】
1 2 | The slowest run took 48.42 times longer than the fastest. This could mean that an intermediate result is being cached. 100000 loops, best of 3: 4.24 µs per loop |
これは、空のリストファイル(du = [])を用意しておいて、appendを使って要素をリストに格納しています。
でも、この書き方はappendを毎回呼び出しているため計算時間のロスが生じているのですよね。
例2)appendを使わない
1 2 3 4 5 6 7 8 | %%timeit import numpy as np du = [] u = np.array((0, 1, 2, 3, 4, 5)) du = np.array([i for i in u]) |
【結果】
1 2 | The slowest run took 8.96 times longer than the fastest. This could mean that an intermediate result is being cached. 100000 loops, best of 3: 4.02 µs per loop |
わずかですが、appendを使うときよりも計算時間が速くなっていますよね。
これくらいの計算規模だと気にしない程度の計算速度ですが、大規模な計算になったときに計算速度の最適化は考えてコードを組んだ方が良いので、色々試行錯誤をして「こうすると速いよ」っていう書き方は覚えておく方がいいでしょう。
以上、余談でした!
スライスと使うときはndarray配列で使う
Pythonの勉強し始めのころは、要素ごとの演算のつもりがなぜか要素の結合になってしまったり、ndarray配列とリスト配列を全然区別できていませんでした。
【ポイント】
- ndarray配列は要素ごとの演算
- リスト型は要素の結合
また、少し余談になりますが大事なところなので、解説しておこうと思います。
ndarray配列は要素ごとの演算
まずは、ndarray配列の生成方法を復習します。
ndarrayオブジェクトの生成方法は以下の3つを覚えておけば良いでしょう(^^)/
※はじめ、慣れないうちはtypeでデータの型を確認しながら進めた方が良いです。
例1)arrayを使う
1 2 3 4 5 6 7 8 | import numpy as np list = [0, 1, 2, 3, 4, 5] u = np.array(list) print(u) print(type(u)) |
【結果】
1 2 | [0 1 2 3 4 5] <class 'numpy.ndarray'> |
例2)linspace(始め:終わり:要素数)を使う
1 2 3 4 5 6 | import numpy as np u = np.linspace(0,10,11) print(u) print(type(u)) |
【結果】
1 2 | [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.] <class 'numpy.ndarray'> |
例3)arange(始め:終わり:分割幅)を使う
1 2 3 4 5 6 | import numpy as np u = np.arange(0,10,1) print(u) print(type(u)) |
【結果】
1 2 | [0 1 2 3 4 5 6 7 8 9] <class 'numpy.ndarray'> |
さらに詳しく知りたい方は、以下の記事も参考にしてください。
ndarrayオブジェクトを使えば、以下のように要素ごとの演算を行ってくれます。
1 2 3 4 5 6 7 8 9 10 | import numpy as np u1 = np.linspace(0,10,5) u2 = np.linspace(0,20,5) u3 = u1 + u2 print('u1 = ', u1) print('u2 = ', u2) print('u3 = ', u3) |
【結果】
1 2 3 | u1 = [ 0. 2.5 5. 7.5 10. ] u2 = [ 0. 5. 10. 15. 20.] u3 = [ 0. 7.5 15. 22.5 30. ] |
めちゃくちゃ直感的に計算できて便利ですよね。
しかし、注意点として配列の要素数同士の演算を行うとエラーがおこるので注意してください。
例えば、以下のコードはエラーが生じます。
1 2 3 4 5 6 7 8 9 10 | import numpy as np u1 = np.linspace(0,10,5) u2 = np.linspace(0,20,3) u3 = u1 + u2 print('u1 = ', u1) print('u2 = ', u2) print('u3 = ', u3) |
【結果】
1 2 3 4 5 6 7 8 9 10 | --------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-31-d9d3a3b2b5ca> in <module>() 4 u2 = np.linspace(0,20,3) 5 ----> 6 u3 = u1 + u2 7 8 print('u1 = ', u1) ValueError: operands could not be broadcast together with shapes (5,) (3,) |
最後の行を見ると、要素の大きさが違うってエラーが書かれていますよね。
失敗した原因は「u1 = np.linspace(0,10,5)」は要素数が5個に対して、「u2 = np.linspace(0,20,3)」は要素数が3個だからです。
エラーの内容は要素数の異なるもの同士を足し算しようとしたからですね。
こんな感じで、ndarrayの演算は要素の数にお気を付けくださいってことです!
リスト型は要素の結合
次に、リストを用意します。
1 2 3 4 | list = [0, 1, 2, 3, 4, 5] print(list) print(type(list)) |
【結果】
1 2 | [0, 1, 2, 3, 4, 5] <class 'list'> |
ここで注意なのですが、リスト型同士の足し算はリストの要素の結合になってしまいます。
1 2 3 4 5 6 | list_1 = [0, 1, 2, 3, 4, 5] list_2 = [0, 1, 2, 3, 4, 5] list_3 = list_1 + list_2 print(list_3) print(type(list_3)) |
【結果】
1 2 | [0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5] <class 'list'> |
なので、リスト同士の足し算は、各リストの要素の数は違ってもエラーになりません。
1 2 3 4 5 6 | list_1 = [0, 1, 2] list_2 = [0, 1, 2, 3, 4, 5] list_3 = list_1 + list_2 print(list_3) print(type(list_3)) |
【結果】
1 2 | [0, 1, 2, 0, 1, 2, 3, 4, 5] <class 'list'> |
しかし、ndarrayのノリで以下の計算をリストのまま行うと、要素の結合になってしまうので注意が必要です。
リストのまま演算をしてしまった例
1 2 3 4 5 | import numpy as np u = [0, 1, 2, 3, 4, 5] list = u[1:] + u[0:-1] print(list) |
【結果】
1 | [1, 2, 3, 4, 5, 0, 1, 2, 3, 4] |
こんな感じで「思ってた計算結果と違う!」ってなるのでここはよく理解しておきましょう。
ndarray配列で演算
1 2 3 4 5 | import numpy as np u =np.array( [0, 1, 2, 3, 4, 5]) list = u[1:] + u[0:-1] print(list) |
【結果】
1 | [1 3 5 7 9] |
やりたいのはこんな感じで「要素ごとの演算」ですよね。
説明が長くなりましたが、初学者だった3年くらい前の自分はこのあたりを理解できていなかったので、詳しくまとめておきました。
では、今度は、スライスを使って実際に2次元の移流方程式を数値計算で解いてみます。
2次元の移流方程式の数値計算
1次元の移流方程式については、以下の記事でまとめてあります。
で、今回は2次元の移流方程式に拡張して数値計算を実装します。
\(x\)方向、\(y\)方向の流れに対して流速を\(u(x,y,t\)と\(v(x,y,t\)と書くと、解くべき方程式は以下になります。
\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x}=0\\
\frac{\partial v}{\partial t}+c\frac{\partial v}{\partial x}=0\tag{1}
\end{align*}
これを離散化して数値計算を行います。移流項の離散化は前回の記事でも同じで後退差分で行います。
u^{n+1}_{i,j}=u^{n}_{i,j}-\frac{c\Delta t}{\Delta x}\big(u^{n}_{i,j}-u^{n}_{i-1,j}\big)-\frac{c\Delta t}{\Delta y}\big(u^{n}_{i,j}-u^{n}_{i,j-1}\big)\\
v^{n+1}_{i,j}=v^{n}_{i,j}-\frac{c\Delta t}{\Delta y}\big(v^{n}_{i,j}-v^{n}_{i-1,j}\big)-\frac{c\Delta t}{\Delta y}\big(v^{n}_{i,j}-v^{n}_{i,j-1}\big)\tag{2}
\end{align*}
初期状態を設定して、for文とスライスを使って解く場合の計算時間を比較してみようと思います。
【手順】
- 初期状態の設定
- (例1)for文で解く
- (例2)スライスで解く
では、まず正気状態を設定します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | import numpy as np nx = 81 ny = 81 nt = 100 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) sigma = .2 dt = sigma * dx x = np.linspace(0, 2, nx) y = np.linspace(0, 2, ny) u = np.ones((ny, nx)) ##create a 1xn vector of 1's un = np.ones((ny, nx)) ###Assign initial conditions u[int(.5 / dy): int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2 |
どんな初期状態になっているのか確認をしておきましょう。
1 2 3 | import matplotlib.pyplot as plt plt.plot(x,u[:,int(.5 / dy)]) |
これで初期状態を作ることができました。
for文を使う
次に普通にfor文を使って時間に対して0~nt+1ステップの計算をさせて計算時間を測定してみます。
0~nt+1ステップの1ステップごとにx−y空間のfor文を2回使うことになりますね。
考えただけでも計算時間がかかりそうなアルゴリズムです・・・
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | %%timeit u = np.ones((ny, nx)) u[int(.5 / dy): int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt + 1): ##loop across number of time steps un = u.copy() row, col = u.shape for j in range(1, row): for i in range(1, col): u[j, i] = (un[j, i] - (c * dt / dx * (un[j, i] - un[j, i - 1])) - (c * dt / dy * (un[j, i] - un[j - 1, i]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 |
※計算時間の計測のためなのて、vについては今回は解いていません(2次元の数値計算については詳しくは次回の記事で解説をします)
1 | 1 loop, best of 3: 2.96 s per loop |
計算時間「2.96 s」でした。約3秒かかるということですね。
スライスを使う
次に、スライスを使って計算を実行してみます。
1 2 3 4 5 6 7 8 9 10 11 12 13 | %%timeit u = np.ones((ny, nx)) u[int(.5 / dy): int(1 / dy + 1), int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt + 1): ##loop across number of time steps un = u.copy() u[1:, 1:] = (un[1:, 1:] - (c * dt / dx * (un[1:, 1:] - un[1:, 0:-1])) - (c * dt / dy * (un[1:, 1:] - un[0:-1, 1:]))) u[0, :] = 1 u[-1, :] = 1 u[:, 0] = 1 u[:, -1] = 1 |
【結果】
1 | 100 loops, best of 3: 4.19 ms per loop |
計算時間が「4.19 ms」となりました。
for文を使った場合よりも1000倍くらい計算時間が短いという結果でしょうか。
このように、for文を使って要素を一つ一つ取り出すという計算方法はどうも時間がかかるようです。
今後は、スライスを使った計算方法による高速化で数値計算をするようにします(^^)/
まとめ
今回は、スライスを使った計算の高速化について解説しました。
繰り返しになりますが、Pythonをインタプリタ型の言語なのでコードの書き方によって計算時間を短縮することができます。
本記事の中で高速化の工夫について出てきたのは以下の2つです。
- for文を使わずにスライスを使う
- appendは使わずにリストの中でfor文を使う
積極的に使う方が良いでしょうね(‘ω’)
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
(本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません)
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと!!って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学1年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値計算を勉強したい方
それをいかに誤差が少なく、安定的に解くかがカギになっており、数値的解法は多く提案されています。