こんにちは(@t_kun_kamakiri)。
本日は、「1次元のバーガース方程式」をPythonで実装するというのをやります。
前回の記事までで、「1次元の移流方程式」「1次元の拡散方程式」をPythonで実装するというのをやりました。
ちょっとずつナビエストークス方程式の実装に近づいています!
「とりあえず、Pythonを使ってナビエストークス方程式を解いてみたい!」という方には、この記事シリーズはとても勉強になるのではないかと思います。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
- 一次元のバーガース方程式の説明
- 一次元のバーガース方程式をPythonを使って数値計算
Burgers方程式・・・衝撃波とからんでて、ここ不勉強だった。
この絶版になった本に詳しく書いてた。 pic.twitter.com/ZwVn98Saa9
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) 2020年5月8日
コードを書きながら理解を深めていきたいと思います。
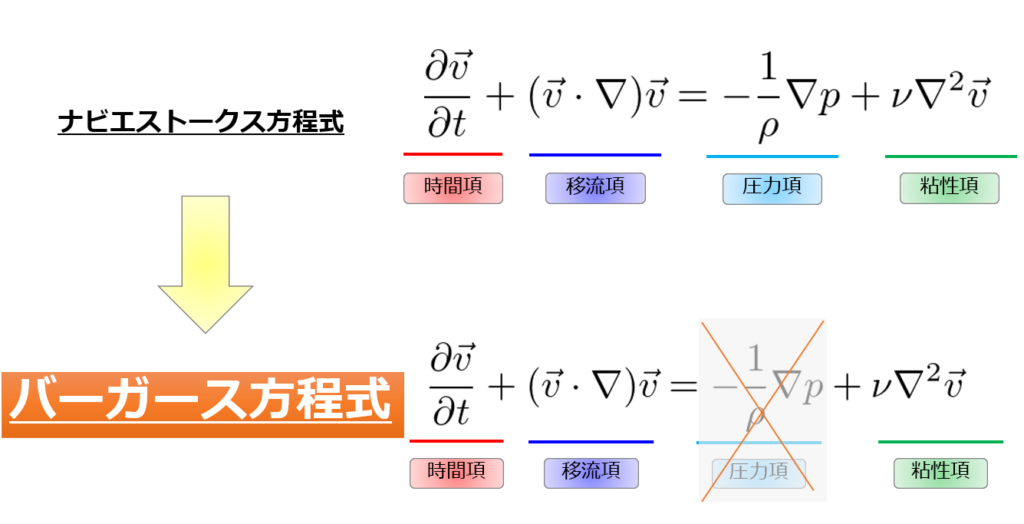
バーガース方程式とは
バーガース方程式は、ナビエストークス方程式において移流項が圧力項より十分大きい場合\(|(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}|>>|\frac{1}{\rho}\nabla p|\)において近似される以下の式で記述されます。
1次元のバーガース方程式
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2}
\end{align*}
圧力項より移流項の方が十分大きいとは、例えば流速がものすごく大きい極音速領域や流速の空間変動が急激な場合などが考えられます。
以下に、いくつかバーガース方程式の特徴を列挙しておきます。
バーガース方程式は奥が深いですが、本記事では「ま~とりあえず肩の力を抜いてPythonを使ってみようよ」っていうスタンスで行こうかと思います(^^)/
1次元バーガース方程式をPythonで実装する
基本的な内容はこちらのサイトに従って進めます。
本記事では、バーガース方程式の解析解と数値計算の結果を比較するというのをします。
バーガース方程式の解析解は、以下の記事をご参考ください。
まずはバーガース方程式の解析解について解説し、その後に解析解ではなくバーガース方程式の数値計算を行って、
解析解 v.s 数値解
と比較を行いたいと思います。
バーガース方程式の解析解
では、まずやることを整理します。
- 初期状態の設定
- 時刻\(t\)での解析解
- sympyを使って解析解の数値計算
1.初期状態の設定
初期状態ですが、以下のような状態とします。
初期状態
u&=-\frac{2\nu}{\phi}\frac{\partial \phi}{\partial x}+4\\
&or\\
u&=-2\nu\frac{\partial }{\partial x}\log\phi+4\tag{1}
\end{align*}
\phi = \exp \bigg(\frac{-x^2}{4 \nu} \bigg) + \exp \bigg(\frac{-(x-2 \pi)^2}{4 \nu}\bigg)\tag{2}
\end{align*}
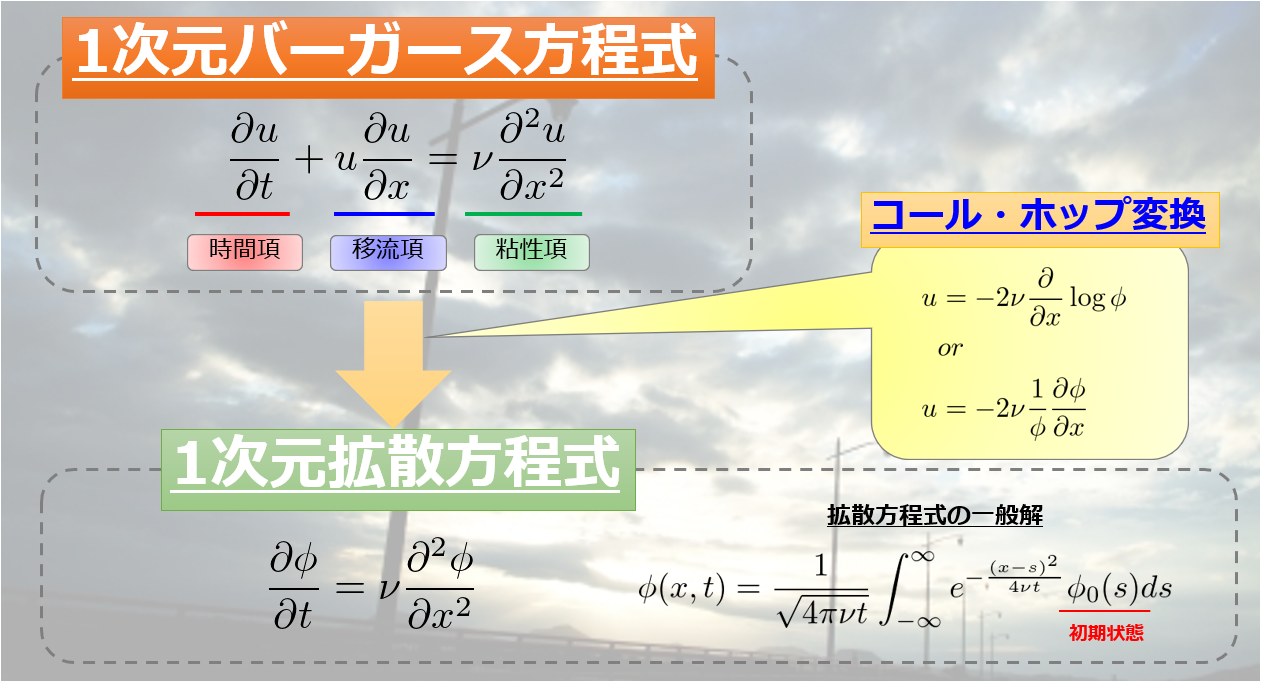
(1)式は、初見だと少々わかりにきですが、コール・ホップ変換の形をしていますね。
これが初期状態です。
u(0) = u(2\pi)
\end{align*}
初期状態の流速\(u\)の形が知りたい場合は、(2)を(1)に代入すれば良いです・・・・が、
計算が少々複雑になってあまり良い情報を得られないので以下のように考えてみます。
まず、(2)式を以下の2項に分けます。
\phi=\phi_1+\phi_2
\end{align*}
\phi_1 &= \exp \bigg(\frac{-x^2}{4 \nu} \bigg) \\
\phi_2 &= \exp \bigg(\frac{-(x-2 \pi)^2}{4 \nu}\bigg)
\end{align*}
\(\phi_1\)と\(\phi_2\)を別々で描くとどうなるでしょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np import matplotlib.pyplot as plt nu = 1 x = np.arange(-np.pi,3*np.pi,0.1) phi1 = np.exp(-x**2/(4*nu)) phi2 = np.exp(-(x-2*np.pi)**2/(4*nu)) plt.plot(x,phi1,label='phi1') plt.plot(x,phi2,label='phi2') plt.legend() plt.grid() plt.xlabel('x',fontsize=16) |
【結果】
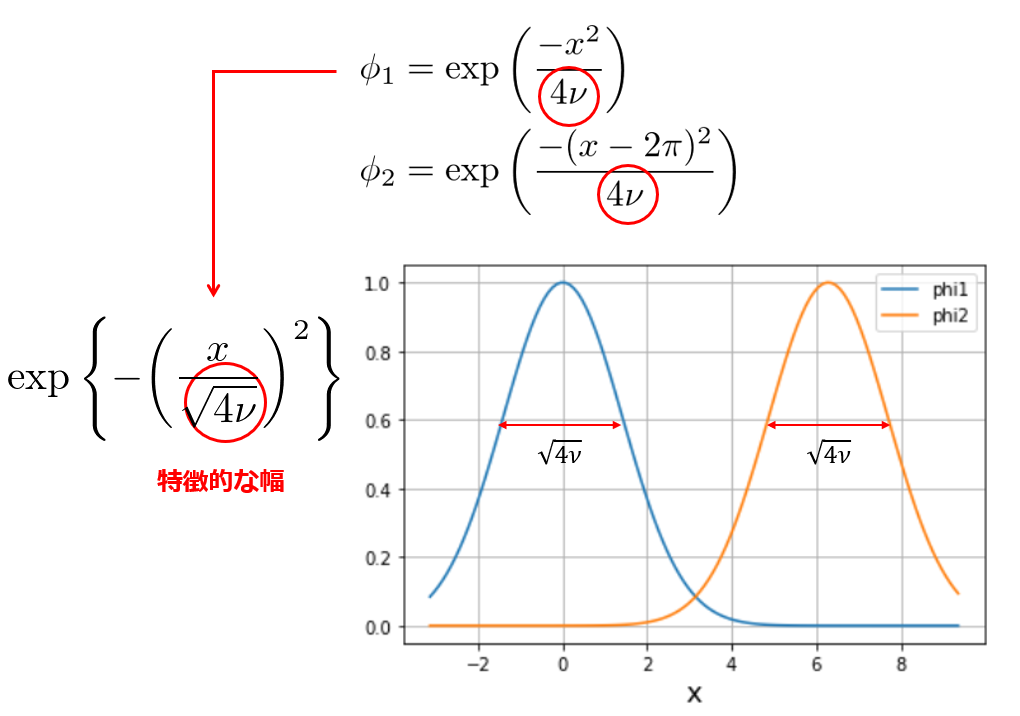

今、「\(\nu=1\)」としているので各関数\(\phi_1,\phi_2\)の特徴的な幅は\(\sqrt{4\nu}=2\)となります。
このように\(\sqrt{4\nu}<2\pi\)であれば、\(\phi_1\)や\(\phi_2\)の裾野が広がった端の方では互いに影響し合わないのがわかるでしょうか。つまり、大雑把な振る舞いを知りたい場合には、\(\phi_1\)と\(\phi_2\)は互いに独立に扱って、\(u\)の形を探っても良いですよね。
なので、まずは\(u=-2\nu\frac{\partial }{\partial x}\log\phi_1+4\)だけを考えてみます。
u&=-2\nu\frac{\partial }{\partial x}\log\left \{\exp \bigg(\frac{-x^2}{4 \nu} \bigg)\right \}+4\\
u&=x+4\tag{3}
\end{align*}
そして、\(\phi_2\)については(3)式を\(x\rightarrow x-2\pi\)にするだけですので、その2つの\(u_1,u_2\)を描くと以下のようになります。
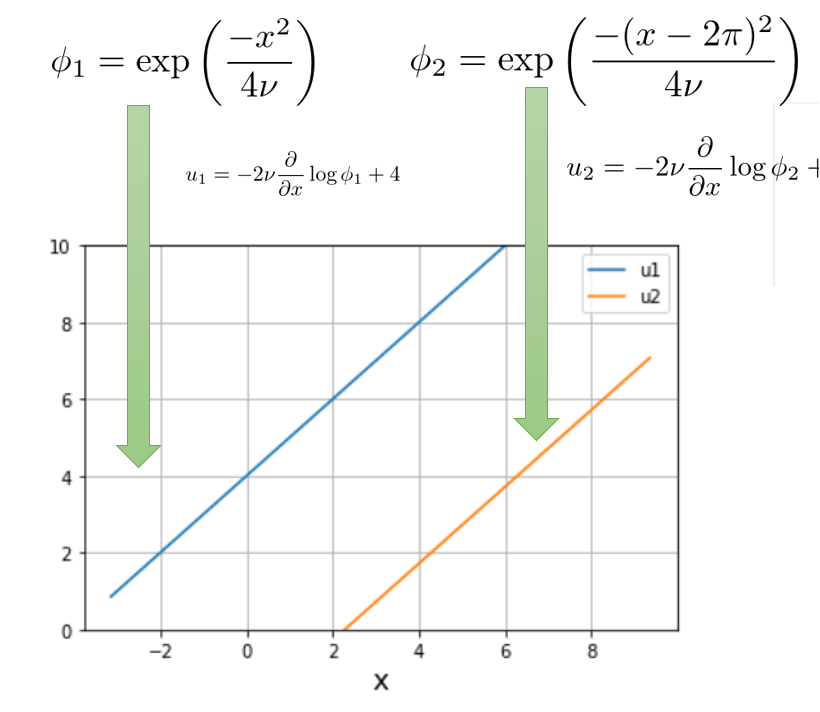
間の不連続な部分をつないで\(u\)の形が完成されます。


この赤線が\(u\)の初期状態です。
\(u=x+4\)の4を足しているのはあまり本質的なことではないので0でも良かったと思うのですが、こちらのサイト通りに従っているので仕方なくこのままいきましょうかね(‘_’)
2.時刻\(t\)での解析解
では、時刻\(t\)での解析解はどのようになるでしょうか?
こちらのサイト通り書くと以下のようになります。
u &=& -\frac{2 \nu}{\phi} \frac{\partial \phi}{\partial x} + 4 \\\
\phi &=& \exp \bigg(\frac{-(x-4t)^2}{4 \nu (t+1)} \bigg) + \exp \bigg(\frac{-(x-4t -2 \pi)^2}{4 \nu(t+1)} \bigg)\tag{4}
\end{eqnarray}
3.sympyを使って解析解の数値計算
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import sympy from sympy.utilities.lambdify import lambdify x, nu, t = sympy.symbols('x nu t') phi = (sympy.exp(-(x - 4 * t)**2 / (4 * nu * (t + 1))) + sympy.exp(-(x - 4 * t - 2 * sympy.pi)**2 / (4 * nu * (t + 1)))) phiprime = phi.diff(x) u = -2 * nu * (phiprime / phi) + 4 ufunc = lambdify((t, x, nu), u) print(ufunc(1, 4, 3)) print(u) |
【結果】
|
1 |
-2*nu*(-(-8*t + 2*x)*exp(-(-4*t + x)**2/(4*nu*(t + 1)))/(4*nu*(t + 1)) - (-8*t + 2*x - 4*pi)*exp(-(-4*t + x - 2*pi)**2/(4*nu*(t + 1)))/(4*nu*(t + 1)))/(exp(-(-4*t + x - 2*pi)**2/(4*nu*(t + 1))) + exp(-(-4*t + x)**2/(4*nu*(t + 1)))) |
- x, nu, t = sympy.symbols(‘x nu t’)とすると、指定した文字をシンボル(変数を表す文字)として扱うことができます。
- lambdify((t, x, nu), u)は「lambdify(変数,関数)」を入れることで、\(u(x)\)を作成しています。
※今の場合は、\(tと\nu\)も変数に入れています。
※さらに詳しく知りたい方は公式ドキュメントをお読みください。 - \(u(t,x,\nu)\)なので、例えば「ufunc(1, 4, 3)」とすることで変数の値を代入して\(u\)の値を出力することができます。
以上で、sympyを使って関数を作成できたので実際に初期状態や時刻\(t\)での\(u\)グラフを描いてみましょう。
まずは、\(t=0\)の初期状態からです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
from matplotlib import pyplot as plt import numpy as np %matplotlib inline #条件設定 nx = 101 nt = 100 dx = 2 * np.pi / (nx - 1) nu = 0.07 dt = dx * nu #初期状態 x = np.linspace(0, 2 * np.pi, nx) un = np.empty(nx) t = 0 u = np.asarray([ufunc(t, x0, nu) for x0 in x]) |
【結果】
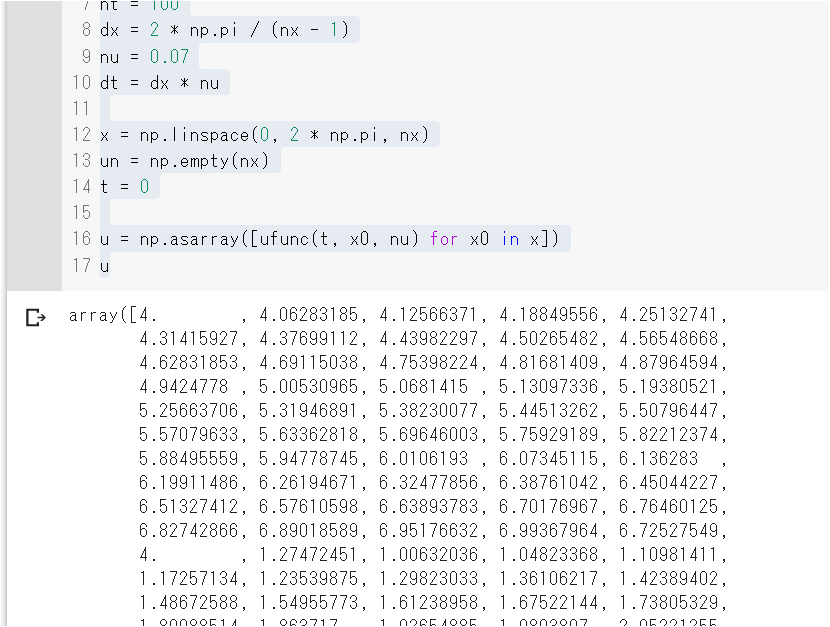

uを出力するとこのようにndarrayのリストとして出力されるのが確認できます。
- ufunc(t, x0, nu)は上で「ufunc = lambdify((t, x, nu), u)」として作成した関数です。
- t=0として初期状態を出力しています。※tを任意の値にすることで時刻tでの解析解のプロファイルを出力することができます。
これをMatplotlibでグラフ化すれば良いですね。
|
1 2 3 4 5 6 7 |
plt.figure(figsize=(11, 7), dpi=100) plt.plot(x, u, marker='o', lw=2) plt.xlim([0, 2 * np.pi]) plt.ylim([0, 10]) plt.grid() plt.xlabel('x',fontsize=16) plt.ylabel('u',fontsize=16) |
【結果】

ちゃんと周期境界条件になっていますよね。
次に、Pythonを使ってバーガース方程式の数値計算を行います。
Pythonでバーガース方程式を実装
今度は、解析解ではなくバーガース方程式を離散化して得られる数値解を見ていきます。
まず、バーガース方程式の離散化は以下のようにします。
\begin{eqnarray}
u_i^{n+1} = u_i^n – u_i^n \frac{\Delta t}{\Delta x} (u_i^n – u_{i-1}^n) + \nu \frac{\Delta t}{\Delta x^2}(u_{i+1}^n – 2u_i^n + u_{i-1}^n)\tag{5}
\end{eqnarray}
離散化する前の導出は特に記載はしませんが、
- 空間に対する一階微分は「後退差分」
- 空間に対する2階微分は「中心差分」
- 時間に対する1階微分は「前進差分」
で行っています。
以下に、Pythonのコードを書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
from matplotlib import pyplot as plt import numpy as np %matplotlib inline #条件設定 nx = 101 nt = 100 dx = 2 * np.pi / (nx - 1) nu = 0.07 dt = dx * nu #初期状態 x = np.linspace(0, 2 * np.pi, nx) un = np.empty(nx) t = 0 u = np.asarray([ufunc(t, x0, nu) for x0 in x]) #バーガース方程式の数値計算 for n in range(nt): un = u.copy() for i in range(1, nx-1): u[i] = un[i] - un[i] * dt / dx *(un[i] - un[i-1]) + nu * dt / dx**2 *\ (un[i+1] - 2 * un[i] + un[i-1]) u[0] = un[0] - un[0] * dt / dx * (un[0] - un[-2]) + nu * dt / dx**2 *\ (un[1] - 2 * un[0] + un[-2]) u[-1] = u[0] |
エラーがなければ特に何も起こりません。
これでバーガース方程式の数値計算が終了して最終状態の\(u\)の値がuという変数に格納されているはずです。
では、このバーガース方程式を離散化した数値計算結果と先ほど求めた解析解との比較を以下でしたいと思います。
解析解と数値解の比較
まずは、解析解の最終状態を「u_analytical」に格納します。
|
1 2 |
#最終状態の解析解 u_analytical = np.asarray([ufunc(nt * dt, xi, nu) for xi in x]) |
- ufunc(nt * dt, xi, nu)はlambdify((t, x, nu), u)のところでやった「lambdify(変数,関数)」です。
- np.asarrayの中にfor文を入れる書き方ができます。
このようにすることでappendを使ってひとつひとつの値をリストに入れていくよりも計算がはやくなります。
では、先ほど求めた数値解も合わせて以下でグラフ化してみましょう。
|
1 2 3 4 5 6 7 8 9 |
plt.figure(figsize=(11, 7), dpi=100) plt.plot(x,u, marker='o', lw=2, label='Computational') plt.plot(x, u_analytical, label='Analytical') plt.xlim([0, 2 * np.pi]) plt.ylim([0, 10]) plt.grid() plt.xlabel('x',fontsize=16) plt.ylabel('u',fontsize=16) plt.legend(); |
【結果】
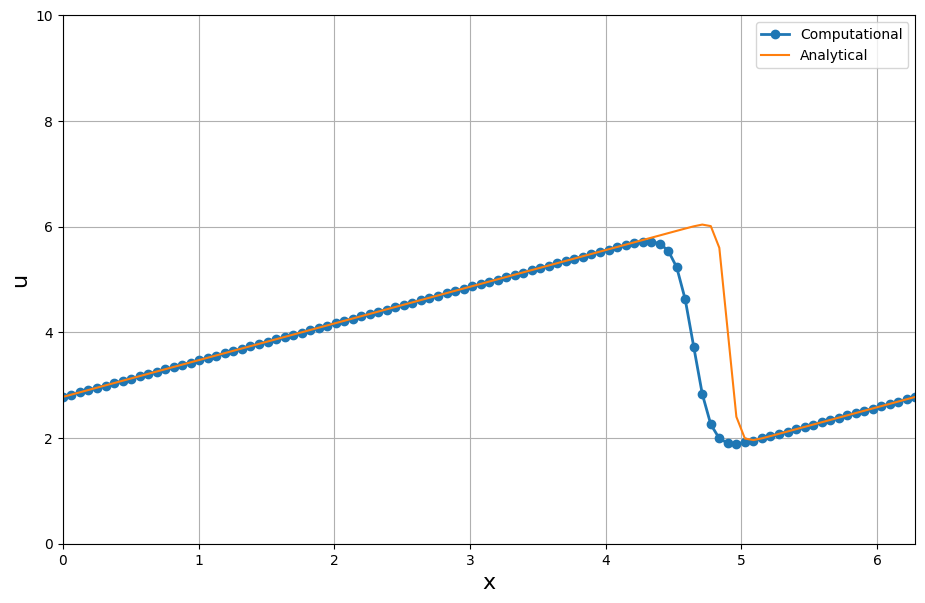
解析解の方が厳密な解なので数値計算の方が微分を離散化したことによる誤差が生じているという事になります。
そういえば、「1次元の移流方程式」でやったように数値解が少し拡散しながら解かれてしまうというのを確認しましたが、その影響がここでも出ているのかもしれません(いわゆる数値粘性というやつですかね)
アニメーション作成
静止画よりもアニメーションを見たいですよね。
というわけでアニメーションも作成してみました(^^♪
以下が、バーガース方程式を離散化して得られる数値解のアニメーションのPythonコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
from matplotlib import pyplot as plt import numpy as np from matplotlib import animation, rc from IPython.display import HTML ###variable declarations nx = 101 nt = 100 dx = 2 * np.pi / (nx - 1) nu = 0.07 dt = dx * nu print('dx=',dx) print('dt=',dt) x = np.linspace(0, 2 * np.pi, nx) un = np.empty(nx) t = 0 u = np.asarray([ufunc(t, x0, nu) for x0 in x]) fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) for i in range(1, nx-1): u[i] = un[i] - un[i] * dt / dx *(un[i] - un[i-1]) + nu * dt / dx**2 *\ (un[i+1] - 2 * un[i] + un[i-1]) u[0] = un[0] - un[0] * dt / dx * (un[0] - un[-2]) + nu * dt / dx**2 *\ (un[1] - 2 * un[0] + un[-2]) u[-1] = u[0] # u_analytical = numpy.asarray([ufunc(nt * dt, xi, nu) for xi in x]) plt.grid() plt.xlim([0.0,2*np.pi]) plt.ylim([-0.1,10]) plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) rc('animation', html='jshtml') plt.close() anim |
まとめ
- 一次元のバーガース方程式の説明
- 一次元のバーガース方程式をPythonを使って数値計算
最後に「解析解と数値解」の比較を行いましたが、数値解の方が拡散しながら解かれてしまうという事がわかりました(これは今後の課題)
では、また(^^)/


























詳しい解説ありがとうございます。
一つ気になることがあるのですが、dt = dx * nuで定義されていますがなぜでしょうか?
ご教授いただけますと幸いです。
ブログお読みいただきありがとうございました。
こちらは陽解法で解いたときの解の安定条件と関係しています。
今回の陽解法(右辺はステップ数nの値のみ)のような数値計算においては、dxに対してdtはある条件でないと不安定になってしまいます。
こちらの記事に似た内容を書いています。
https://takun-physics.net/7395/
今回は元記事(https://github.com/barbagroup/CFDPython/blob/master/lessons/05_Step_4.ipynb)の内容通りにしたので、正確な意図はくみ取れませんが、少なくともdtに関しては、
dxをが決めた時点でc=nu*dt/dx**2 < 1/2が安定条件なのでdt = (1/2)*dx**2/nuよりも小さい値にしておけば良いと思います。
ありがとうございます!理解できました。
どの記事も詳しく実例を示しながら書いて下さっているので本当にわかりやすいです。
これからもブログ参考にさせていただきます。