【OpenFOAMカスタマイズ】icoFoamに温度場輸送方程式を追加。

前回の記事でも書いた通り、OpenFOAMのカスタマイズできるように勉強をはじめています。

前回の記事はこちら

【オープンソース流体解析】OpenFOAMカスタマイズしたいので準備をしています。

今はまだネット上にあるOpenFOAMのカスタマイズ記事を自分で理解しながら手を動かして進めているだけなので、記事の内容的に目新しいものはありませんのでご了承ください。

本記事の内容は、こちらの記事を参考にして自分でもまとめなおしています。
自分で理解して記事にしたりとアウトプットをすると理解が深まります。

それに、まとめなおしていってもOpenFOAMのバージョンや仕様が違うとソースコードの中身が違うので注意が必要ですね。
参考記事の方は、「OpenFOAM6(Foundation版)」ですが、僕の使用環境はESI版の「OpenFOAM-v1912」で行っていますし、何よりWSLでやっています。

【使用環境】
Windows10
WSL (Windows Subsystem for Linux)
OpenFOAM-v1912

今回は、上記の環境で行いましたが参考記事通りにすると問題なく動きました。

また、OpenFOAMのバージョンは古いですがDEXCSのOpenFOAMをカスタマイズしたときの資料もあります。

やりたいこと：ベースで解く方程式+追加する方程式
全体の流れを確認
ライブラリの修正
ソースコードの修正
1. ソースコードのコンパイル
ケースファイルの修正
計算実行
結果確認
まとめ
C++の勉強について
OpenFOAMの参考書

やりたいこと：ベースで解く方程式+追加する方程式

まずは、今回の目的（やりたいこと）を確認しておきましょう。

【やりたいこと】

icoFoamのソルバに温度場の輸送方程式を追加する。

では、偏微分方程式を確認します。

ナビエストークス方程式

\begin{align*}
\frac{\partial \boldsymbol{u}}{\partial t}+\big(\boldsymbol{u}\cdot\nabla\big)\boldsymbol{u}= -\frac{1}{\rho}\nabla p+\nu \nabla^2\boldsymbol{u} \tag{1}
\end{align*}

👆これがもともとicoFoamで解く偏微分方程式です
ここに、以下の温度場輸送方程式を導入します。

温度場輸送方程式

\begin{align*}
\frac{\partial \boldsymbol{T}}{\partial t}+\big(\boldsymbol{u}\cdot\nabla\big)\boldsymbol{T}= D_t \nabla^2\boldsymbol{T} \tag{2}
\end{align*}

$D_t =\frac{k}{\rho C_p}$と置いています。

$k$：熱伝導率
$C_p$：定圧比熱
$\rho$：密度

icoFoamってもともとどんな用途のためのソルバなのか？って思った場合は以下の表を参考にすれば良いでしょう。

OpenFOAMの「非圧縮性流体ソルバ」を以下に示しておきます。

参考サイト

非圧縮性流体
adjointShapeOptimizationFoam	定常/非ニュートン流体の乱流/随伴方程式を使用することで障害物による圧損を考慮してダクト形状を最適化
boundaryFoam	定常/1次元乱流/通常は流入口での境界層条件の生成に使用
icoFoam	非定常/ニュートン流体の層流
nonNewtonianIcoFoam	非定常/非ニュートン流体の層流
pimpleFoam	非定常/時間刻み幅大/（PISOとSIMPLEを組み合わせた）PIMPLEアルゴリズム
pimpleDyMFoam	非定常/移動メッシュ/（PISOとSIMPLEを組み合わせた）PIMPLEアルゴリズム
SRFPimpleFoam	非定常/時間刻み幅大/単一の回転領域
pisoFoam	非定常/PISOアルゴリズム
shallowWaterFoam	非定常/回転を伴う非粘性の浅水方程式
simpleFoam	定常
porousSimpleFoam	定常/多孔質体（陰解法・陽解法）有りの乱流/MRF（Multiple Reference Frame）機能を使用可能
SRFSimpleFoam	定常/単一の回転領域

この中で今回は「icoFoam」という、非定常・非圧縮性の流れを扱う際に使うソルバをベースにします。

非圧縮性の流体は基本的には温度場は解きません。
なぜなら、知りたい物理量は「流速$\boldsymbol{u}$」と「圧力$p$」の２つであり、解くべき方程式「運動量保存則」と「質量保存則」の２つです。

なので、方程式自体が閉じいるので温度を解く必要がないですし、密度変化が小さい非圧縮性の仮定が成り立つような状況において温度変化による密度への影響というのはとても小さいので温度を考える必要がないというのもあります。

こちらの記事もどうぞ

非圧縮性流体の基礎方程式

温度変化することによる密度変化を考慮しないといけない場合は、有名なのはブシネスク近似と呼ばれるものですが、ここでは深い話はしません。

以下の２点を頭においてくださればと思います。

温度が流れに沿って移動する方程式（温度の輸送方程式）を追加する。
温度が変化したことによる流速への影響は考慮していない。

全体の流れを確認

OpenFOAMのファイル構造は詳しくは理解していないですが、わからないなりに理解をしながら進めたいと思っています。

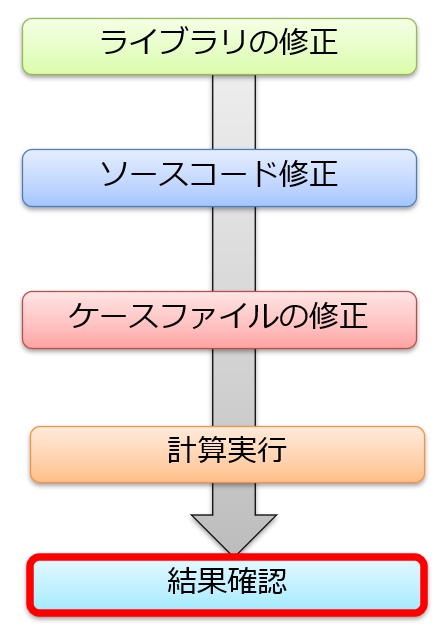
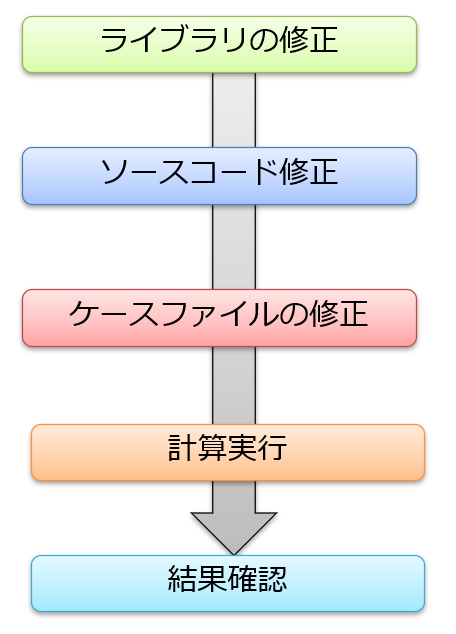
まず、今回やることの全体像は以下です。

各ステップの説明は、その都度する予定です。

今は、全体像を把握しておくだけで良いでしょう。

ライブラリの修正

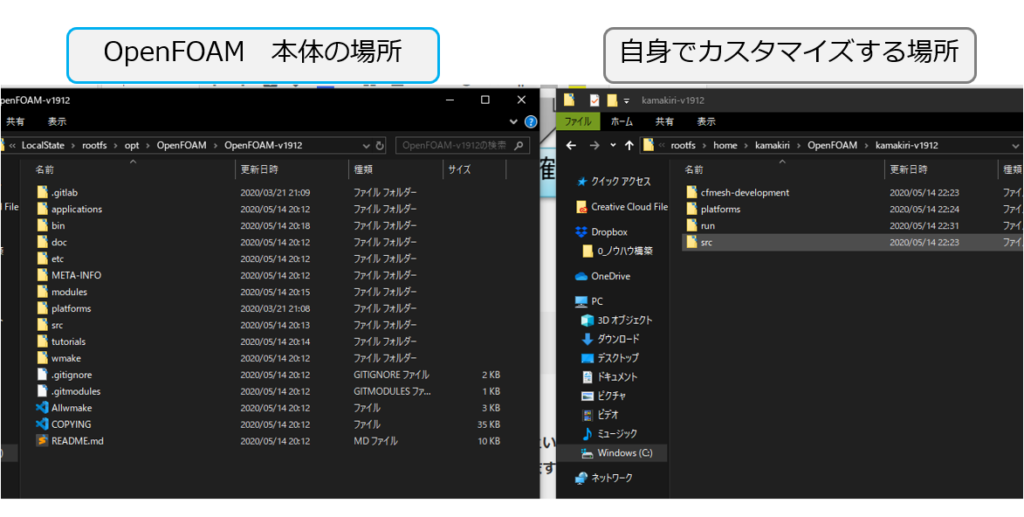
自身でカスタマイズする部分のライブラリは、環境変数「$WM_PROJECT_USER_DIR」というフォルダに作成していきます。
OpenFOAMの本体のライブラリは、環境変数「 $WM_PROJECT_DIR」にあります。

環境変数は前回の記事☟でまとめてありますので、確認しながら進めていってください。

前回の記事はこちら

【オープンソース流体解析】OpenFOAMカスタマイズしたいので準備をしています。

環境変数が九人出来たら、実際にどのフォルダを指しているのかをWindows上でフォルダ移動して中身を確認してみればよいです。
絵の右側のフォルダに自身のカスタマイズしたいライブラリやソルバをぽいぽい入れていきます。

OpenFOAM本体と同じようなフォルダ構造を意識しながら、今回は「 /home/kamakiri/OpenFOAM/kamakiri-v1912/applications/solvers/incompressible/」を自身のカスタマイズしたフォルダに作成します。

作業ディレクトリを作成する

前回の記事でも書きましたが、WSL上でOpenFOAMのフォルダ・ファイル作成・コピー・削除を行うにはLinux上から行うのが安全です。

前回の記事はこちら

【オープンソース流体解析】OpenFOAMカスタマイズしたいので準備をしています。

Windows上でフォルダ作成してもファイルに権限が付与されていないなど、権限を付与したりする手間があるので以下ではLinuxのコメンドベースでフォルダを操作していきます。

【やること】

フォルダ移動：「/home/kamakiri/OpenFOAM/kamakiri-v1912」へ移動
ファイル作成：「/solvers/incompressible」を作成

ターミナル上で以下のコマンドを打ちます。

cd $WM_PROJECT_USER_DIR
mkdir -p applications/solvers/incompressible

1 2	cd $WM_PROJECT_USER_DIR mkdir -p applications/solvers/incompressible

ファイルできているか確認してみましょう。

フォルダの権限も確認しておきます。

ちゃんと権限が付与されています。

ベースコードを作業ディレクトリに複製する

では、ベースとなるソースコードを自身の作業ディレクトリにコピーしてソースコードを編集する準備をします。

【やること】

ベースのコードを自身のカスタマイズフォルダへコピーする
フォルダ名「icoFoam」を「my_icoFoam」に変更
「icoFoam.C」を「my_icoFoam.C」に変更

ターミナル上で以下のコマンドを打ちます。

cp -r /opt/OpenFOAM/OpenFOAM-v1912/applications/solvers/incompressible/icoFoam/ /home/kamakiri/OpenFOAM/kamakiri-v1912/applications/solvers/incompressible/

1	cp -r /opt/OpenFOAM/OpenFOAM-v1912/applications/solvers/incompressible/icoFoam/ /home/kamakiri/OpenFOAM/kamakiri-v1912/applications/solvers/incompressible/

フォルダがコピーされているか確認してみましょう。

コピーできていますね。

この「icoFoam」を「my_icoFoam」という名前に変えます。

ターミナル上で以下のコマンドを打ちます。

cd /home/kamakiri/OpenFOAM/kamakiri-v1912/applications/solvers/incompressible/
mv icoFoam my_icoFoam

1 2	cd /home/kamakiri/OpenFOAM/kamakiri-v1912/applications/solvers/incompressible/ mv icoFoam my_icoFoam

これでフォルダ名が変わりました。

では、「icoFoam.C」を「my_icoFoam.C」に変更

cd my_icoFoam
mv icoFoam.C my_icoFoam.C

1 2	cd my_icoFoam mv icoFoam.C my_icoFoam.C

ファイル名が変わっていることを確認しましょう。

温度場輸送方程式のヘッダーファイルを準備

次に、温度場輸送方程式をC++で追加します。

温度場輸送方程式

\begin{align*}
\frac{\partial \boldsymbol{T}}{\partial t}+\big(\boldsymbol{u}\cdot\nabla\big)\boldsymbol{T}= D_t \nabla^2\boldsymbol{T} \tag{2}
\end{align*}

【やること】

「TEeq.H」に温度場輸送方程式のコードを追加する。

ターミナル上で以下のコマンドを打って「TEeq.H」ファイルを作成します。

touch TEeq.H

1	touch TEeq.H

「TEeq.H」ファイルの中身は以下のようにしておきます。

「TEeq.H」

solve
(
 fvm::ddt(T)
 + fvm::div(phi, T)
 - fvm::laplacian(Dt, T)
);

solve

(

fvm::ddt(T)

+ fvm::div(phi, T)

- fvm::laplacian(Dt, T)

);

編集は、Windows上のテキストエディタを使って良いです。
僕はVisual Stdio Codeを使っています。

※ちゃんと編集がLinux上で反映されているか心配な方は、「vi」コマンドでファイルの中身を確認してみても良いです。

 vi TEeq.H

vi TEeq.H

いちおうちゃんとファイルの中身は反映されています。

※後々説明しますが、これを「my_icoFoam.C」でIncludeします。

「Dt（拡散係数）」と「T（温度）」の定義を行う

【やること】

「createField.H」に「Dt（拡散係数）」と「T（温度）」の変数定義。

「createField.H」
※「//Add here…」～「//Add End」までを追加します。

Info<< "Reading transportProperties\n" << endl;

IOdictionary transportProperties
(
    IOobject
    (
        "transportProperties",
        runTime.constant(),
        mesh,
        IOobject::MUST_READ_IF_MODIFIED,
        IOobject::NO_WRITE
    )
);

dimensionedScalar nu
(
    "nu",
    dimViscosity,
    transportProperties
);

Info<< "Reading field p\n" << endl;
volScalarField p
(
    IOobject
    (
        "p",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);


Info<< "Reading field U\n" << endl;
volVectorField U
(
    IOobject
    (
        "U",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);

//Add here...
dimensionedScalar Dt
(
"Dt",
dimViscosity,
transportProperties.lookup("Dt")
);
//Done for now...
Info<< "Reading field T\n" <<endl;
volScalarField T
(
IOobject
(
"T",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
//Add End

#include "createPhi.H"


label pRefCell = 0;
scalar pRefValue = 0.0;
setRefCell(p, mesh.solutionDict().subDict("PISO"), pRefCell, pRefValue);
mesh.setFluxRequired(p.name());

Info<< "Reading transportProperties\n" << endl;

IOdictionary transportProperties

(

IOobject

(

"transportProperties",

runTime.constant(),

mesh,

IOobject::MUST_READ_IF_MODIFIED,

IOobject::NO_WRITE

)

);

dimensionedScalar nu

(

"nu",

dimViscosity,

transportProperties

);

Info<< "Reading field p\n" << endl;

volScalarField p

(

IOobject

(

"p",

runTime.timeName(),

mesh,

IOobject::MUST_READ,

IOobject::AUTO_WRITE

mesh

);

Info<< "Reading field U\n" << endl;

volVectorField U

(

IOobject

(

"U",

runTime.timeName(),

mesh,

IOobject::MUST_READ,

IOobject::AUTO_WRITE

mesh

);

//Add here...

dimensionedScalar Dt

(

"Dt",

dimViscosity,

transportProperties.lookup("Dt")

);

//Done for now...

Info<< "Reading field T\n" <<endl;

volScalarField T

(

IOobject

(

"T",

runTime.timeName(),

mesh,

IOobject::MUST_READ,

IOobject::AUTO_WRITE

mesh

);

//Add End

#include "createPhi.H"

label pRefCell = 0;

scalar pRefValue = 0.0;

setRefCell(p, mesh.solutionDict().subDict("PISO"), pRefCell, pRefValue);

mesh.setFluxRequired(p.name());

残念なことにC++の知識がないため、説明ができないですが「Dt（拡散係数）」と「T（温度）」の変数定義を行ったんだな～っていうのはわかりました。

ソースコードの修正

「createField.H」も「TEeq.H」もソースコードと言えばそうなのですが、今から修正する「my_icoFoam.C」は偏微分方程式を解いているメインのコードで、「createField.H」と「TEeq.H」をヘッダーファイルとして読み込んでいるファイルなので、いちおう区別しておきました。

【やること】

「my_icoFoam.C」に「TEeq.H」を読み込む。

「my_icoFoam.C」の中に、温度場輸送方程式を解く部分「TEeq.H」を読み込むようにすれば良いです。

my_icoFoam.C

/*---------------------------------------------------------------------------*\
  =========                 |
  \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox
   \\    /   O peration     |
    \\  /    A nd           | www.openfoam.com
     \\/     M anipulation  |
-------------------------------------------------------------------------------
    Copyright (C) 2011-2016 OpenFOAM Foundation
    Copyright (C) 2019 OpenCFD Ltd.
-------------------------------------------------------------------------------
License
    This file is part of OpenFOAM.

    OpenFOAM is free software: you can redistribute it and/or modify it
    under the terms of the GNU General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.

    OpenFOAM is distributed in the hope that it will be useful, but WITHOUT
    ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
    FITNESS FOR A PARTICULAR PURPOSE.  See the GNU General Public License
    for more details.

    You should have received a copy of the GNU General Public License
    along with OpenFOAM.  If not, see <http://www.gnu.org/licenses/>.

Application
    icoFoam

Group
    grpIncompressibleSolvers

Description
    Transient solver for incompressible, laminar flow of Newtonian fluids.

    \heading Solver details
    The solver uses the PISO algorithm to solve the continuity equation:

        \f[
            \div \vec{U} = 0
        \f]

    and momentum equation:

        \f[
            \ddt{\vec{U}}
          + \div \left( \vec{U} \vec{U} \right)
          - \div \left(\nu \grad \vec{U} \right)
          = - \grad p
        \f]

    Where:
    \vartable
        \vec{U} | Velocity
        p       | Pressure
    \endvartable

    \heading Required fields
    \plaintable
        U       | Velocity [m/s]
        p       | Kinematic pressure, p/rho [m2/s2]
    \endplaintable

\*---------------------------------------------------------------------------*/

#include "fvCFD.H"
#include "pisoControl.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    argList::addNote
    (
        "Transient solver for incompressible, laminar flow"
        " of Newtonian fluids."
    );

    #include "postProcess.H"

    #include "addCheckCaseOptions.H"
    #include "setRootCaseLists.H"
    #include "createTime.H"
    #include "createMesh.H"

    pisoControl piso(mesh);

    #include "createFields.H"
    #include "initContinuityErrs.H"

    // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

    Info<< "\nStarting time loop\n" << endl;

    while (runTime.loop())
    {
        Info<< "Time = " << runTime.timeName() << nl << endl;

        #include "CourantNo.H"

        // Momentum predictor

        fvVectorMatrix UEqn
        (
            fvm::ddt(U)
          + fvm::div(phi, U)
          - fvm::laplacian(nu, U)
        );

        #include "TEeq.H"
        
        if (piso.momentumPredictor())
        {
            solve(UEqn == -fvc::grad(p));
        }

        // --- PISO loop
        while (piso.correct())
        {
            volScalarField rAU(1.0/UEqn.A());
            volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
            surfaceScalarField phiHbyA
            (
                "phiHbyA",
                fvc::flux(HbyA)
              + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
            );

            adjustPhi(phiHbyA, U, p);

            // Update the pressure BCs to ensure flux consistency
            constrainPressure(p, U, phiHbyA, rAU);

            // Non-orthogonal pressure corrector loop
            while (piso.correctNonOrthogonal())
            {
                // Pressure corrector

                fvScalarMatrix pEqn
                (
                    fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
                );

                pEqn.setReference(pRefCell, pRefValue);

                pEqn.solve(mesh.solver(p.select(piso.finalInnerIter())));

                if (piso.finalNonOrthogonalIter())
                {
                    phi = phiHbyA - pEqn.flux();
                }
            }

            #include "continuityErrs.H"

            U = HbyA - rAU*fvc::grad(p);
            U.correctBoundaryConditions();
        }

        runTime.write();

        runTime.printExecutionTime(Info);
    }

    Info<< "End\n" << endl;

    return 0;
}


// ************************************************************************* //

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

/*---------------------------------------------------------------------------*\

========= |

\\ / F ield | OpenFOAM: The Open Source CFD Toolbox

\\ / O peration |

\\ / A nd | www.openfoam.com

\\/ M anipulation |

-------------------------------------------------------------------------------

License

This file is part of OpenFOAM.

OpenFOAM is free software: you can redistribute it and/or modify it

under the terms of the GNU General Public License as published by

the Free Software Foundation, either version 3 of the License, or

(at your option) any later version.

OpenFOAM is distributed in the hope that it will be useful, but WITHOUT

ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or

FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License

for more details.

You should have received a copy of the GNU General Public License

along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>.

Application

icoFoam

Group

grpIncompressibleSolvers

Description

Transient solver for incompressible, laminar flow of Newtonian fluids.

\heading Solver details

The solver uses the PISO algorithm to solve the continuity equation:

\f[

\div \vec{U} = 0

\f]

and momentum equation:

\f[

\ddt{\vec{U}}

+ \div \left( \vec{U} \vec{U} \right)

- \div \left(\nu \grad \vec{U} \right)

= - \grad p

\f]

Where:

\vartable

\vec{U} | Velocity

p | Pressure

\endvartable

\heading Required fields

\plaintable

U | Velocity [m/s]

p | Kinematic pressure, p/rho [m2/s2]

\endplaintable

\*---------------------------------------------------------------------------*/

#include "fvCFD.H"

#include "pisoControl.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])

{

argList::addNote

(

"Transient solver for incompressible, laminar flow"

" of Newtonian fluids."

);

#include "postProcess.H"

#include "addCheckCaseOptions.H"

#include "setRootCaseLists.H"

#include "createTime.H"

#include "createMesh.H"

pisoControl piso(mesh);

#include "createFields.H"

#include "initContinuityErrs.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

Info<< "\nStarting time loop\n" << endl;

while (runTime.loop())

{

Info<< "Time = " << runTime.timeName() << nl << endl;

#include "CourantNo.H"

// Momentum predictor

fvVectorMatrix UEqn

(

fvm::ddt(U)

+ fvm::div(phi, U)

- fvm::laplacian(nu, U)

);

#include "TEeq.H"

if (piso.momentumPredictor())

{

solve(UEqn == -fvc::grad(p));

}

// --- PISO loop

while (piso.correct())

{

volScalarField rAU(1.0/UEqn.A());

volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));

surfaceScalarField phiHbyA

(

"phiHbyA",

fvc::flux(HbyA)

+ fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)

);

adjustPhi(phiHbyA, U, p);

// Update the pressure BCs to ensure flux consistency

constrainPressure(p, U, phiHbyA, rAU);

// Non-orthogonal pressure corrector loop

while (piso.correctNonOrthogonal())

{

// Pressure corrector

fvScalarMatrix pEqn

(

fvm::laplacian(rAU, p) == fvc::div(phiHbyA)

);

pEqn.setReference(pRefCell, pRefValue);

pEqn.solve(mesh.solver(p.select(piso.finalInnerIter())));

if (piso.finalNonOrthogonalIter())

{

phi = phiHbyA - pEqn.flux();

}

#include "continuityErrs.H"

U = HbyA - rAU*fvc::grad(p);

U.correctBoundaryConditions();

}

runTime.write();

runTime.printExecutionTime(Info);

}

Info<< "End\n" << endl;

return 0;

}

// ************************************************************************* //

「TEeq.H」を速度Uの偏微分方程式を解いている真下に追加しました。

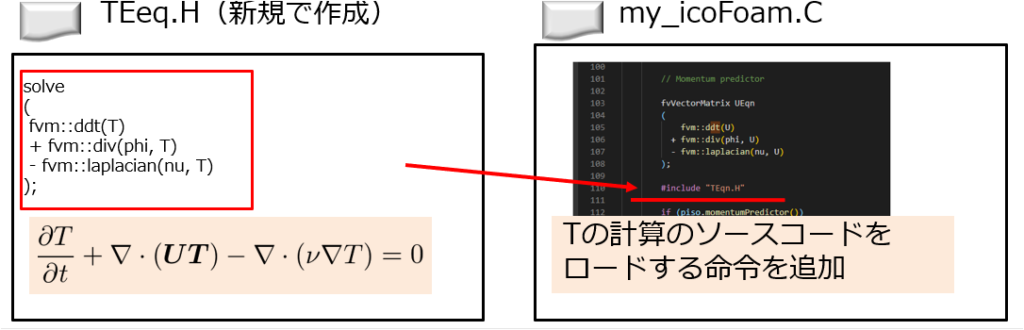
C++のコードは理解していないですが、どこが時間発展のループを回りしている部分かはわかります。

これで一応ソースコードができました。

次に、この作成したソースコードをコンパイルする必要があります。

ソースコードのコンパイル

ソースコードは人間が読み書きできるプログラミング言語で書かれているのですが、それを機械が理解できるいわゆる「機械語」ってやつに変換する必要があります。

それは「Make」フォルダの中のファイルを編集することで行うことができます。

【やること】

「Make」フォルダの中の「files」を編集する。
ソースコードのコンパイルして実行ファイルを作成

files

my_icoFoam.C
EXE = $(FOAM_USER_APPBIN)/my_icoFoam

1 2	my_icoFoam.C EXE = $(FOAM_USER_APPBIN)/my_icoFoam

わかりにくいですが、以下の内容を書いていると理解しました。

どのソースコードをコンパイルする？：my_icoFoam.C
どこにコンパイルしてどこに何という名前で実行ファイルを保存する？：$(FOAM_USER_APPBIN)/my_icoFoam

「$FOAM_USER_APPBIN」という環境変数がわからない場合は、「echo $FOAM_USER_APPBIN」で調べてみましょう。

環境変数	値
$FOAM_USER_APPBIN	/home/kamakiri/OpenFOAM/kamakiri-v1912/platforms/linux64Gcc63DPInt32Opt/bin

どうやら「/home/kamakiri/OpenFOAM/kamakiri-v1912/platforms/linux64Gcc63DPInt32Opt/bin」に「my_icoFoam」という実行ファイルが作成されるようです。

ソースコードのコンパイルには、「my_icoFoam」上で「wmake」とします。

ターミナルで以下のコンパイルを打ちます。

wmake

wmake

すると以下のような表示がされます。

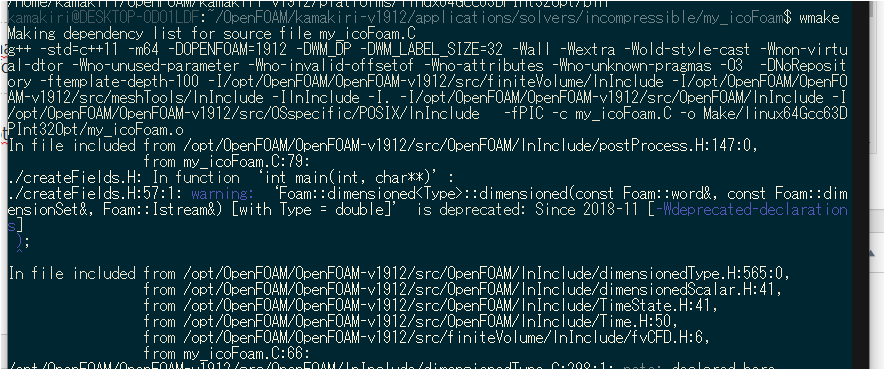
これで「my_icoFoam」という名前の実行ファイルが作成できたと思います。

実行ファイルが確認できたかを確認するには「which」コマンドで実行ファイルの場所の保存場所を確認してみればよいでしょう。

which my_icoFoam

1	which my_icoFoam

どうやら「/home/kamakiri/OpenFOAM/kamakiri-v1912/platforms/linux64Gcc63DPInt32Opt/bin/」の中に「my_icoFoam」という実行ファイルが作成されているようですね。

これは、filesで「EXE = $(FOAM_USER_APPBIN)/my_icoFoam」と設定したことによってこのようになったということです。

※ちなみに「wmake」をすると以下のような、フォルダとファイルが作成されています。

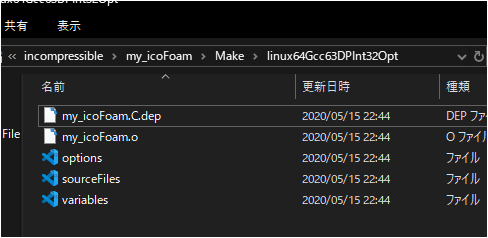
「wmake」したときにエラーなどが生じてコンパイルをやり直したい場合は、こちらのファイルを削除する必要があります。
それには「wclean」と打てばフォルダが消えます。

wclean

wclean

以上で、OpenFOAMでのC++で書かれたソースコードの修正を行うことができました。

これで、温度場の輸送方程式も解くことができるようになりましたが・・・

OpenFOAMのケースファイルの方も「Dt（拡散係数）」「T（温度）」の設定を追加しなくてはいけません。

ケースファイルの修正

では、ケースファイルに「DT（拡散係数）」と「T（温度）」を追加します。

【やること】

OpenFOAMチュートリアルのケースファイルを自身の作業ディレクトリにコピーする。
T(温度）の境界条件の設定
Dt（拡散係数）の定義
温度場の解き方の設定（fvSchemes、fvSolution）

まずは、「OpenFOAMチュートリアルのケースファイルを自身の作業ディレクトリにコピー」をします。

以下のように、ターミナルに打つことでOpenFOAMのチュートリアルを自身の作業ディレクトリにコピーすることができます。

その際には、以下の環境変数を利用すると便利です。

$FOAM_TUTORIALS
$FOAM_RUN

cp -r /opt/OpenFOAM/OpenFOAM-v1912/tutorials/incompressible/icoFoam/cavity/cavity /home/kamakiri/OpenFOAM/kamakiri-v1912/run/20200515_my_icoFoam_cavity

1	cp -r /opt/OpenFOAM/OpenFOAM-v1912/tutorials/incompressible/icoFoam/cavity/cavity /home/kamakiri/OpenFOAM/kamakiri-v1912/run/20200515_my_icoFoam_cavity

自身の作業ディレクトリは「20200515_my_icoFoam_cavity」としています。

コピーできているかを確認してみましょう。
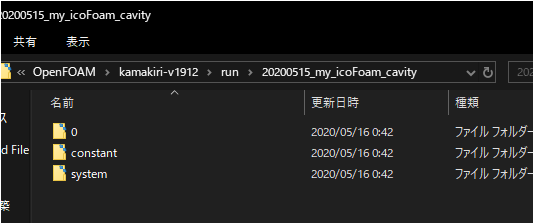
まず「20200515_my_icoFoam_cavity」というフォルダができています。

そして、「20200515_my_icoFoam_cavity」の中身は、

こうなっています。

OpenFOAMのチュートリアルをコピーできています。

次に、この作業ディレクトリに移ります。

cd $FOAM_RUN

1	cd $FOAM_RUN

と打てば、「/home/kamakiri/OpenFOAM/kamakiri-v1912/run」に移動することができます。

あとは、「cd」コマンドでフォルダ移動を行ってください。

T(温度）の境界条件の設定

温度の設定は、「0」というフォルダの中の「p」ファイルを「T」という名前でコピーします。

cp -r p T

cp -r p T

ファイルの中身は以下のようにします。

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  v1912                                 |
|   \\  /    A nd           | Website:  www.openfoam.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    object      T;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

dimensions   [0 0 0 1 0 0 0];

internalField   uniform 300;

boundaryField
{
    movingWall
    {
        type fixedValue;
        value uniform 350;
    }

    fixedWalls
    {
        type fixedValue;
        value uniform 300;
    }

    frontAndBack
    {
        type            empty;
    }
}

// ************************************************************************* //

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: v1912 |

| \\ / A nd | Website: www.openfoam.com |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class volScalarField;

object T;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

dimensions [0 0 0 1 0 0 0];

internalField uniform 300;

boundaryField

{

movingWall

{

type fixedValue;

value uniform 350;

}

fixedWalls

{

type fixedValue;

value uniform 300;

}

frontAndBack

{

type empty;

}

// ************************************************************************* //

Dt（拡散係数）の定義

拡散係数の定義は「constant」の中の「transportProperties」というファイルを編集します。

constant/transportProperties

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  v1912                                 |
|   \\  /    A nd           | Website:  www.openfoam.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      transportProperties;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

nu              0.01;

Dt [0 2 -1 0 0 0 0] 0.002;

// ************************************************************************* //

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: v1912 |

| \\ / A nd | Website: www.openfoam.com |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class dictionary;

location "constant";

object transportProperties;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

nu 0.01;

Dt [0 2 -1 0 0 0 0] 0.002;

// ************************************************************************* //

「Dt [0 2 -1 0 0 0 0] 0.002;」という定義を追加しました。

次に、温度の輸送方程式をどのように解くかという設定を追加します。
そのためには、「system/fvSchemes」と「system/fvSolution」の２つのファイルを編集します。

system/fvSchemes

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  v1912                                 |
|   \\  /    A nd           | Website:  www.openfoam.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      fvSchemes;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

ddtSchemes
{
    default         Euler;
}

gradSchemes
{
    default         Gauss linear;
    grad(p)         Gauss linear;
}

divSchemes
{
    default         none;
    div(phi,U)      Gauss linear;
    div(phi,T)      Gauss upwind; 
}

laplacianSchemes
{
    default         Gauss linear orthogonal;
}

interpolationSchemes
{
    default         linear;
}

snGradSchemes
{
    default         orthogonal;
}


// ************************************************************************* //

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: v1912 |

| \\ / A nd | Website: www.openfoam.com |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class dictionary;

location "system";

object fvSchemes;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

ddtSchemes

{

default Euler;

}

gradSchemes

{

default Gauss linear;

grad(p) Gauss linear;

}

divSchemes

{

default none;

div(phi,U) Gauss linear;

div(phi,T) Gauss upwind;

}

laplacianSchemes

{

default Gauss linear orthogonal;

}

interpolationSchemes

{

default linear;

}

snGradSchemes

{

default orthogonal;

}

// ************************************************************************* //

「div(phi,T) Gauss upwind;」としています。

これは$\nabla\cdot(\boldsymbol{U}T)$の移流項を解く部分の設定です。

system/fvSolution

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  v1912                                 |
|   \\  /    A nd           | Website:  www.openfoam.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      fvSolution;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

solvers
{
    p
    {
        solver          PCG;
        preconditioner  DIC;
        tolerance       1e-06;
        relTol          0.05;
    }
    //add this...
    T
    {
        solver PBiCG;
        preconditioner DILU;
        tolerance 1e-7;
        relTol 0;
    };

    pFinal
    {
        $p;
        relTol          0;
    }

    U
    {
        solver          smoothSolver;
        smoother        symGaussSeidel;
        tolerance       1e-05;
        relTol          0;
    }
}

PISO
{
    nCorrectors     2;
    nNonOrthogonalCorrectors 0;
    pRefCell        0;
    pRefValue       0;
}


// ************************************************************************* //

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: v1912 |

| \\ / A nd | Website: www.openfoam.com |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class dictionary;

location "system";

object fvSolution;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

solvers

{

solver PCG;

preconditioner DIC;

tolerance 1e-06;

relTol 0.05;

}

//add this...

{

solver PBiCG;

preconditioner DILU;

tolerance 1e-7;

relTol 0;

};

pFinal

{

$p;

relTol 0;

}

{

solver smoothSolver;

smoother symGaussSeidel;

tolerance 1e-05;

relTol 0;

}

PISO

{

nCorrectors 2;

nNonOrthogonalCorrectors 0;

pRefCell 0;

pRefValue 0;

}

// ************************************************************************* //

温度場の解き方を追加しました。

これでケースファイルの編集は終わりです。

計算実行

では、計算を実行します。

【やること】

「blockMesh」でメッシュ作成
「my_icoFoam」で計算実行

まずは、blockMeshでメッシュ作成します。

blockMesh

blockMesh

問題が無ければ、以下のようになります。

次に、計算を実行します。
自身で作成した温度場輸送方程式も解く「my_icoFoam」という実行ファイルを実行します。

my_icoFoam

1	my_icoFoam

エラーが無ければこのように、「ダーーー」っと計算が流れるのがわかります。

計算がうまくいっていれば以下のように「0.1」「0.2」「0.3」「0.4」「0.5」というフォルダができています。

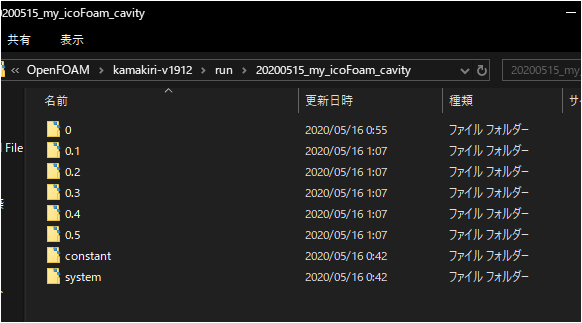
では、温度場が速度に応じて輸送しているのかをparaviewで確認してみましょう。

結果確認

結果確認にはparaviewを使用します。

OpenFOAMの結果を見るためには、以下のように「.foam」という拡張子のファイルを用意してして、それをparaviewで読み込めば結果を表示することができます。

なので、以下のように「a.foam」というからファイルを作成して、paraviewdで結果を表示してみます。

touch a.foam

1	touch a.foam

説明だとわかりにくいので動画を用意しました。

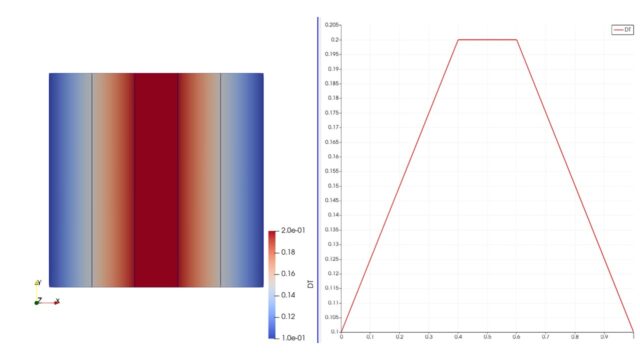
paraviewの表示にも温度「T」が追加されて、温度が速度に乗って解かれているのが確認できますね(^^)/

まとめ

簡単に温度場の輸送方程式をカスタマイズすることができました。
温度場が変化したことによる速度場への影響変化については解いていません。
今回はOpenFOAM v19-12でのカスタマイズを行ったが、バージョンが変わったことによる違いはわからないので今後の追跡調査が必要です。
思い通りのカスタマイズを行うには、OpenFOAMのファイル構成とC++の知識が必要であります。

OpenFOAMの古いバージョンですが、pisoFoamに温度場を追加したケースもやってみました。

C++の勉強について

自分自身がC++の知識が全くないので、いちから勉強する必要があります。

C＋＋は、C言語にオブジェクト指向（クラスなどが使える）を追加して拡張された言語であるとのことなので、まずはC言語から勉強をはじめています。

「Cの絵本」はとてもわかりやすくて、すらすら読めます。
ページ数も多くないので、僕はこれを１週間くらいで読み終えました。

Cの絵本第2版 C言語が好きになる新しい9つの扉

アンク

1,518円(10/30 02:04時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

C言語の環境構築はWSLで使えるようにしています。エディタはVisual Stdio Codeです。
環境構築については、こちらのQiitaの記事が参考になります。

C言語もむちゃくちゃ詳しくなる必要はないと思いますが、一応コードを書いて計算実行したりして理解をしていきました。
「Cの絵本」だけでは詳しいところまでは学べないので、以下の参考書も手元に置いています。

新・明解C言語入門編 (明解シリーズ)

柴田望洋

3,860円(10/30 02:04時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

ページ数も多く詳しく書かれていますし、説明もとてもわかりやすいです。

そして、C言語がそこそこ理解できたらいよいよC++の勉強を始めていきます（👈今、ここ）
同じく「C++の絵本」を買って読もうと思ったのですが、あまりサンプルコードが載っていなかったので読むのをやめました（「Cの絵本」はサンプルコードあったのに・・）

以下の、「猫でもわかるシリーズ」で勉強を進めています。

猫でもわかるC++プログラミング第2版 (猫でもわかるプログラミング)

粂井康孝

2,420円(10/30 02:04時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

これが結構わかりやすいですし、サンプルコードも程よい量で載っています。

あとは、やっぱり詳しいところまで知りたい場合は以下の参考書に頼ります。

新・明解C++入門編 (明解シリーズ)

柴田望洋

3,025円(10/30 16:06時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

あとは、Twitterで教えてもらったこれとかを手元に置いています。

C++の入門書は私はこれがおすすめです…！ページ数は多いですが、わかりやすい分多くなってるイメージです！https://t.co/A1eCYzFHPO
— kurenaif@VTuber (@fwarashi) 2020年5月14日

ロベールのC++入門講座

ロベール

4,054円(10/30 12:51時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

では、OpenFOAMのC++はかなり特殊らしいのですが、C++の基礎知識を身につけないことにはどうしようもないのでまずは２週間程度でC++の基礎を身につけたいと思います(^^)/

OpenFOAMの参考書

OpenFOAMの参考書と言えば、こちらのサイトを書籍にまとめなおした☟これがおすすめです。

OpenFOAMによる熱移動と流れの数値解析(第2版)

3,520円(10/30 04:54時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

OpenFOAMの使用にあたっては「どうやってOpenFOAMをインストールするの？」というところでつまずきます。

そんな時は、以下の書籍をおすすめします。

改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)

川畑真一

3,740円(10/30 16:06時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。
著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。

POSTED COMMENT

uppoi より:
2022年10月12日 08:43
v2006でもできました。ありがとうございます！
返信
- korokoro より:
  2022年10月13日 21:28
  コメントありがとうございます。
  スカラー輸送方程式の追加でしたらこちらの設定でも追加することができるのでご参考ください。
  https://www.openfoam.com/documentation/guides/latest/doc/guide-fos-solvers-scalar-transport.html
  解説付きのケースファイルなどはこちらにあります。
  https://cfd-training.com/2018/08/14/how-to-add-a-passive-scalar-to-your-openfoam-simulations/
  日本語で解説されている記事もご参考ください_(._.)_
  https://qiita.com/takaf05/items/4d3c48d3c125c8275a86
  返信

やりたいこと：ベースで解く方程式+追加する方程式

全体の流れを確認

ライブラリの修正

作業ディレクトリを作成する

ベースコードを作業ディレクトリに複製する

温度場輸送方程式のヘッダーファイルを準備

「Dt（拡散係数）」と「T（温度）」の定義を行う

ソースコードの修正

ソースコードのコンパイル

ケースファイルの修正

計算実行

結果確認

まとめ

C++の勉強について

OpenFOAMの参考書

【OpenFOAMカスタマイズ】空間依存する温度拡散係数に変更

【OpenFOAM】定常流れ＋粒子追跡（カップリング無し）

【OpenFOAM】スロッシングの実験比較（設定ファイル解説あり）

【OpenFOAM】移流方程式で色々な離散化スキームをPythonで自動実行して試してみた

【回転するバスケットボールまわりの流れ(4)】OpenFOAMで無回転の球体まわりの流れ

【OpenFOAM(cyclicAMI)】異なるメッシュの境界で円筒内の流れ

【オープンソースCAE解析】OpenFOAMで流体解析！球体周りの流れ：渦の生成（第1部）

【OpenFOAM(円筒内の流れ)】blockMeshでメッシュ作成(1)

【OpenFOAM】snappyHexMeshを使ったメッシュ境界層がうまくいかない

【OpenFOAM(混相流)】円の液相率で初期状態を作る

【OpenFOAM】snappyHexMesh によるメッシュ再分割の検討

【水面高さ時刻歴データ(OpenFOAM)】ParaViewとPythonでグラフ化する方法(12)

【OpenFOAM】ケルビンヘルムホルツ不安定性の流体解析

【OpenFOAM入門】熱交換器の軸対称モデルでは失敗した

【回転するバスケットボールまわりの流れ(2)】OpenFOAMで無回転のバスケットボールまわりのメッシュ作成

【OpenFOAM球体周りの抗力係数(1)】FreeCADで球体モデルを作る

【OpenFOAMのTips】覚えておくと便利だけど忘れがちなもの

【圧力データ(OpenFOAM)】ParaViewで表示してExcelデータと比較(9)

【3次元ダムブレイク(OpenFOAM)】クーラン数違いによる結果比較

【回転するバスケットボールまわりの流れ(3)】外部領域をblockMeshでメッシュ作成

POSTED COMMENT

COMMENT コメントをキャンセル