こんにちは(@t_kun_kamakiri)。
今日から、Python基礎講座で学んだ内容を使いながら応用編をやっていきます。
応用編では何をするかというと、
👆これを目標にやります。
おそらく記事内容をシリーズ化して、12回程度に分けて記事を作成していきます。
基本的な内容はこちらのサイトにそってやっていきますが、英語に苦手意識がない人は本編のサイトで勉強するのが良いでしょう。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
自分自身が、Pythonを勉強を始めて2年くらい経ちますが、ほとんどPythonを実用的に使う機会がなく(もちろん使いこなせることもなく)、また流体解析の実務経験もないので、素人レベルに近いです。
本編が英語ではあるものの、とても分かりやすかったので日本語に意訳しながら記事にまとめていけば自分の知識も付いてくるかと思ってまとめ始めています。
では、さっそくこの記事では何をするのかというと、
- 本シリーズの目標確認と環境構築の説明
12回にわたって記事にしていきますので、ひとつひとつ読んでいけばPythonを使って流体シミュレーションを体験できます(‘ω’)ノ
このシリーズの最終目標は?
最終的には、以下のような2次元のナビエストークス方程式を使ってキャビティ流れの数値計算をすることを目標にします。
\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v}=-\frac{1}{\rho}\nabla p + \nu \nabla^2\vec{v}\tag{1}
\end{align*}
を離散化して、
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n}-p_{i-1,j}^{n}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)\\
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n}-p_{i,j-1}^{n}}{2\Delta y}
+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{2}
\end{align*}
(2)式を解いて、Pythonのmatplotlibで描写すると以下のようになります。
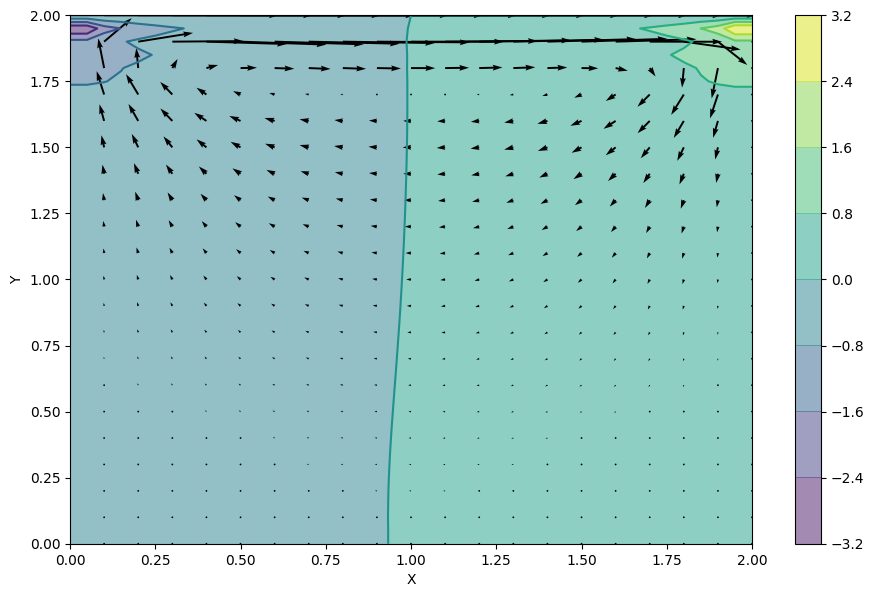
本編はアニメーション作成までやっていないのですが、もちろんPythonのmatplotlibを使ってアニメーション作成だってできます。
(2)式を見ればわかるように、(1)式を単純に差分法で離散化しただけの式です。
ちょっと偏微分方程式の数値計算をかじったことがある人であれば、そこまで抵抗がない離散化手法だと思います。
Pythonの環境構築
※この記事では、Google Colaboratoryを使って進めていきます。
【Pythonの使用環境について】
当ブログはこれをメインに使った計算結果です。
Google ColaboratoryであればGoogleアカウントを持っている人は、Googleの拡張機能を使って簡単にPythonを使うことができます。もしくは、Anacondaを使って進めても問題なく進むと思います。関連記事
もちろん、その他の使用環境でも良いのですが、Pythonで標準に搭載されていないライブラリ(numpy, matplotlib)などがあるため、別途インストールする必要がありちょっと面倒です。
ですが、「Google Colaboratory」と「Anaconda」であればデフォルトでnumpy, matplotlibを使うことができるので環境構築でつまづくことはほぼないでしょう。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
(本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません)
まとめ
本記事では、Pythonを使って流体の数値計算をしていくための環境構築について説明しました。
Pythonはプログラミング初心者にはとっても取っつきやすい言語であり、ネットに多くの情報があります。
他の言語と比べると、だれが書いている記事であろうとそこそこ解読するのに苦労することがなく、とても読みやすいです。
自分自身が「どうやったら計算速度が速くなるのか」などの知見はあまり持っていないので、勉強しつつ調べながらわかったことを記事に追加していく方針です。
今回の記事作成のきっかけは以下です。
Pythonには自分のようなわりと初心者レベルでも高度な使い方ができるライブラリが多く存在しています。
しかし、実際「流体の数値計算を体験してみたいんだが・・・」となったときに、いちから丁寧に解説している書籍は多くありません。
数値計算だけに偏っていたり、プログラミングの重きを置いていたり・・・何より書籍だから有料だし(笑)
今回は、英語だけどせっかく無料で公開されているなら日本語に直してしまおうと考えての行動となります。
直訳というよりは、大まかな流れは本編に従いつつ、ちょっと深堀したいと思った部分も記事に追加して、理解を深めながら最終章まで駆け抜けたいと思っています。
ちなみに最終章まで行っても流体の数値計算はまだまだこれから
最終章まで読んだところで「流体の数値計算」のエキスパートになるのは程遠いでしょう。
なぜなら、実世界の流体現象のほとんどが乱流状態で、一般的には数値計算でしか理論的な予測は不可能です。
というのもナビエストークス方程式が一般解が見つかっておらず、何かしらの近似を使って予測することしかできないのが現状ですが、それが乱流状態となると手計算レベルではもうお手上げです。
昨今は、実用的な範囲では乱流をモデル化して解くことで流体現象の予測を行うことが多いでしょう。
なぜ乱流をモデル化する必要があるのかというと、乱流の構成要素である渦の動きを再現しようと思うと大小さまざまな渦を再現しうるだけの解像度を持って数値計算を行う必要があります。それはとてもつもない要素の数を扱うことになり現実的ではありません。
だから、乱流対して理論的にわかっている部分だけをモデル化して、できるだけ要素を削減して数値計算を行う必要があります。
乱流のモデル化のことを「乱流モデル」と呼ばれており、どのように乱流をモデル化するのかという選択をできる人が流体解析のエキスパートでしょう・・・・
昨今は、実用的な範囲では商用のソフトを使うことが多いでしょう。
- どうやって離散化するのか?
- 計算速度を速めるアルゴリズムは?
- そもそもナビエストークス方程式で良いの?
などを考えて流体現象と向き合うことがとても大事になります。
つまり、本編の最後に示す「2次元ナビエストークス方程式」を空間に対して中心差分と時間に対して前進差分を行う手法だけが流体の全てではないという事です。
☟流体の計算精度や安定性に関しては、こちらの記事を参考に一読してみてください。
何か気づきがあるかもしれません(^^)/
では、環境構築ができたら次の記事に進みましょう。