こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事ではPythonのNumpyの使い方のまとめを書いています。
数値計算において行列を使った計算はよく行いますよね?
この記事では、Pythonを使った行列計算の基礎についての解説を行います。
- Python初心者でNumpyを使い始めている
- Numpyを使った行列計算の基礎を知りたい
ベクトルの表記
ベクトルを列ベクトルで表記すると、
a_{x}\\ a_{y}
\\a_{z}
\end{pmatrix}\tag{1}\end{align*}
となります。
行ベクトルで書く場合は、(1)の転置行列として表記します。
a_{x}& a_{y} & a_{z}
\end{pmatrix}\tag{2}\end{align*}
ベクトルの内積
ベクトルの内積は、2つのベクトルの各成分についての積を足し合わせたものです。
今、2つのベクトルを\(\boldsymbol{a}\)と\(\boldsymbol{b}\)とします。
ベクトルの内積の表記
\boldsymbol{{}^t\!a}\boldsymbol{b}
=\begin{pmatrix}a_{x}& a_{y} & a_{z}\end{pmatrix}\begin{pmatrix}
b_{x}\\ b_{y}\\b_{z}
\end{pmatrix}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}\tag{3}\end{align*}
高校生まではこうしていたかなと思います。
\boldsymbol{a}\cdot \boldsymbol{b}=(a_{x} \,a_{y} \,a_{z})\cdot(b_{x} \,b_{y} \,b_{z})=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}\tag{4}\end{align*}
このように考えても良いでしょう。
ベクトルの内積を計算
例えば次の2つのベクトルの内積を計算してみましょう。
4\\ 5
\\6
\end{pmatrix}\tag{5}\end{align*}
5\\ 3
\\7
\end{pmatrix}\tag{6}\end{align*}
ベクトルの内積は、
\boldsymbol{{}^t\!a}\boldsymbol{b}
=\begin{pmatrix}4& 5 & 6 \end{pmatrix}\begin{pmatrix}
5 \\ 3 \\ 7
\end{pmatrix}=4*5+5*3+6*7=77\tag{7}\end{align*}
Pythonでベクトルの内積「np.inner」を計算
Pythonでベクトルのベクトルの内積は「numpyのinner関数」という関数を使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np list_a=[4,5,6] list_b=[5,3,7] a=np.array(list_a) b=np.array(list_b) print("ベクトルa=",a) print("ベクトルb=",b) c=np.inner(a,b) print("ベクトルaとbの内積=",c) |
先ほどと同様に、実行すると下記のようになります。
|
1 2 3 |
ベクトルa= [4 5 6] ベクトルb= [5 3 7] ベクトルaとbの内積= 77 |
手計算で出した答えと同じですね。
※ちなみに外積は「numpyのcross関数」を使います。
内積が「inner」で、外積が「cross」と覚えておきましょう。
ベクトルの内積のPythonの別表記
ベクトルの内積は「numpyのdot関数」を使っても計算できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np list_a=[4,5,6] list_b=[5,3,7] a=np.array(list_a) b=np.array(list_b) print("ベクトルa=",a) print("ベクトルb=",b) c=np.dot(a,b) print("ベクトルaとbの内積=",c) |
これを実行すると次の答えを返してくれます。
|
1 2 3 |
ベクトルa= [4 5 6] ベクトルb= [5 3 7] ベクトルaとbの内積= 77 |
「nu.dot関数」を使った場合と同じ結果になりましたね。
行列の表記
簡単のために「2行2列の行列」を考えます。
\(A\)という行列は、下記のように表記します。
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}
\end{align*}
Pythonで行列の作成
Pythonでの行列の作成はnumpyのmatrixというメソッドを用います。
2行2列の場合
1 & 2 \\
3 & 4
\end{pmatrix}
\end{align*}
|
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as np #1行目 list_1=[1,2] #2行目 list_2=[3,4] A=np.matrix([list_1,list_2]) print("A行列") print(A) |
実行すると以下を返してくれます。
|
1 2 3 |
A行列 [[1 2] [3 4]] |
4行4列の場合
1 & 2 & 3 & 4\\
5 & 6 & 7 & 8\\
9 & 10 & 11 & 12\\
13 & 14 & 15 & 16
\end{pmatrix}
\end{align*}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np #1行目 list_1=[1,2,3,4] #2行目 list_2=[5,6,7,8] #3行目 list_3=[9,10,11,12] #4行目 list_4=[13,14,15,16] A=np.matrix([list_1,list_2,list_3,list_4]) print("A行列") print(A) |
実行すると以下を返してくれます。
|
1 2 3 4 5 |
A行列 [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12] [13 14 15 16]] |
13行目は下記のように書いても良いです。
|
1 2 3 4 5 |
A=np.matrix([ [1,2,3,4], [5,6,7,8], [9,10,11,12], [13,14,15,16],]) |
こちらの方が行列の書き方に近くてわかりやすいかもしれませんね。
ただリストを並べただけですってことを理解していればこれでも良いかもしれません。
転置行列とは
簡単のために「2行2列の行列」を考えます。
\(A\)という行列は、下記のように表記します。
$$A=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix}\tag{8}$$
\(A\)行列の転置行列は以下のように書きます。
$${}^t\!A=\begin{pmatrix}
a_{11} & a_{21}\\
a_{12} & a_{22}
\end{pmatrix}\tag{9}$$
(8)と比較して行と列が入れ替わっただけです。
Pythonを用いて転置行列を作成
例えば、下記の行列Aの転置行列をPythonで作成してみましょう。
$$A=\begin{pmatrix}
1 & 2 & 3 & 4\\
5 & 6 & 7 & 8\\
9 & 10 & 11 & 12\\
13 & 14 & 15 & 16
\end{pmatrix}\tag{10}$$
np.transposeを使って転置行列を作成
転置行列の作成はとても簡単です。
「numpyの中のtranspose関数」を使って転置行列を作成することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np #1行目 list_1=[1,2,3,4] #2行目 list_2=[5,6,7,8] #3行目 list_3=[9,10,11,12] #4行目 list_4=[13,14,15,16] A=np.matrix([list_1,list_2,list_3,list_4]) t_A=np.transpose(A) print("A行列") print(A) print("Aの転置行列") print(t_A) |
実行結果
|
1 2 3 4 5 6 7 8 9 10 |
A行列 [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12] [13 14 15 16]] Aの転置行列 [[ 1 5 9 13] [ 2 6 10 14] [ 3 7 11 15] [ 4 8 12 16]] |
Tプロパティを使って転置行列を作成
もうひとつの方法としては、np.matrixで作成したmatrix値のTプロパティというのを使って転置行列を作成できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np #1行目 list_1=[1,2,3,4] #2行目 list_2=[5,6,7,8] #3行目 list_3=[9,10,11,12] #4行目 list_4=[13,14,15,16] A=np.matrix([list_1,list_2,list_3,list_4]) tA=A.T print("A行列") print(A) print("Aの転置行列") print(tA) |
実行するとこのように返してくれます。
|
1 2 3 4 5 6 7 8 9 10 |
A行列 [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12] [13 14 15 16]] Aの転置行列 [[ 1 5 9 13] [ 2 6 10 14] [ 3 7 11 15] [ 4 8 12 16]] |
見事に行と列が入れ替わってくれましたね。
出力結果が、
$${}^t\!A=\begin{pmatrix}
1 & 5 & 9 & 13\\
2 & 6 & 10 & 14\\
3 & 7 & 11 & 15\\
4 & 8 & 12 & 16
\end{pmatrix\tag{11}$$
となっていることを確認してください。
行列の積
3行3列の行列\(A\)と\(B\)を考えます。
1 &2 &3 \\
4 &5 &6 \\
7 & 8 &9
\end{pmatrix}\tag{12}\end{align*}
11 &12 &13 \\
14 &15 &16 \\
17 &18 &19
\end{pmatrix}\tag{13}\end{align*}
行列の積とは、
1 &2 &3 \\
4 &5 &6 \\
7 & 8 &9
\end{pmatrix}\begin{pmatrix}
11 &12 &13 \\
14 &15 &16 \\
17 &18 &19
\end{pmatrix}\tag{14}\end{align*}
を計算することになります。
計算方法は、「行列\(A\)の\(i\)行目」と「行列\(B\)の\(j\)列目」の各成分同士の積を足し合わせたものを\(i\)行\(j\)列目に書いていく。
具体的には、下記のようなことを繰り返していきます。
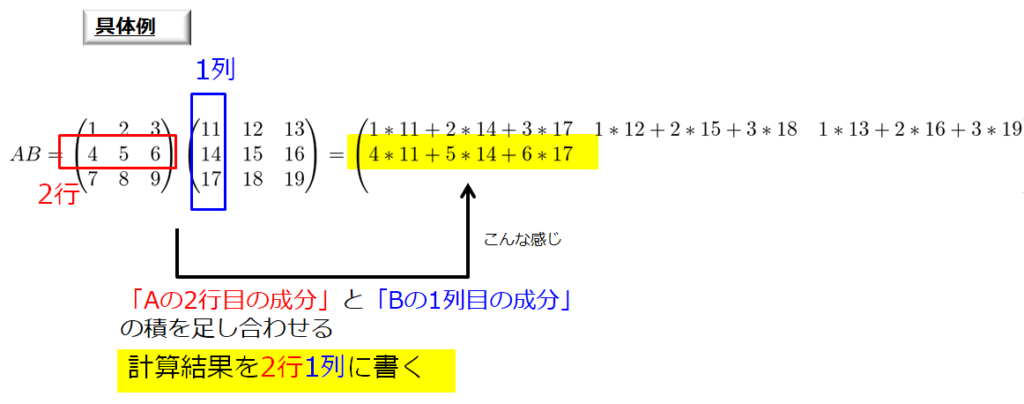
計算するのは結構面倒です。
※行列の積はどのような行列同士でも計算できるわけではありません。
例えば「\(i\)行\(j\)列の行列\(A\)」と「\(m\)行\(n\)列の行列\(B\)」があったとします。
行列の積が計算できるのは、\(i=n\)(一つ目の行列Aの”行”と行列Bの”列”の数が同じ)の場合だけです。
だからこのような場合は計算ができません。
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15
\end{pmatrix}\end{align*}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
\end{pmatrix}\end{align*}
この2つの行列の積
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15
\end{pmatrix}\begin{pmatrix}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
\end{pmatrix}\end{align*}

Pythonでもこの場合は計算エラーが出ます。
Pythonで行列の計算
では、
1 &2 &3 \\
4 &5 &6 \\
7 & 8 &9
\end{pmatrix}\begin{pmatrix}
11 &12 &13 \\
14 &15 &16 \\
17 &18 &19
\end{pmatrix}\tag{15}\end{align*}
の計算をPythonにしてもらいましょう。
Pythonを用いて行列の計算を行うには、「numpyのdot関数」を使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3], [4,5,6], [7,8,9] ]) #行列Bを定義 B=np.matrix([[11,12,13], [14,15,16], [17,18,19] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
実行結果
|
1 2 3 4 |
行列の積C [[ 90 96 102] [216 231 246] [342 366 390]] |
面倒な結果も楽々計算してくれます。
「3行5列の行列」と「5行3列の行列」の積
これも計算はできます。
例えば下記のような2つの行列があったとします。
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15
\end{pmatrix}\tag{16}\end{align*}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
30 &31 &32 \\
33 &33 &35 \\
\end{pmatrix}\tag{17}\end{align*}
この2つの行列の積とは、
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15
\end{pmatrix}\begin{pmatrix}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
30 &31 &32 \\
33 &33 &35 \\
\end{pmatrix}\tag{18}\end{align*}
を計算することになります(手計算はめちゃくちゃめんどうです)
これをPythonで実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3,4,5], [6,7,8,9,10], [11,12,13,14,15] ]) #行列Bを定義 B=np.matrix([[21,22,23], [24,25,26], [27,28,29], [30,31,32], [33,34,35] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
実行結果
|
1 2 3 4 |
行列の積C [[ 435 450 465] [1110 1150 1190] [1785 1850 1915]] |
3行3列の行列が結果として出てきました。
「3行5列の行列」と「3行3列の行列」の積
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15
\end{pmatrix}\begin{pmatrix}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
\end{pmatrix}\end{align*}
を計算してみることにします。
これはエラーが出ます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3,4,5], [6,7,8,9,10], [11,12,13,14,15] ]) #行列Bを定義 B=np.matrix([[21,22,23], [24,25,26], [27,28,29] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
結果は下記のようなエラーが出されてしまいました。
|
1 2 3 4 5 6 7 8 9 |
ValueError Traceback (most recent call last) <ipython-input-16-f50f58ecfad6> in <module>() 14 15 #行列の積(AとBの積) ---> 16 C=np.dot(A,B) 17 18 print("行列の積C") ValueError: shapes (3,5) and (3,3) not aligned: 5 (dim 1) != 3 (dim 0) |
「5行5列の行列」と「3行3列の行列」の積
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15\\
16 &17 &18 &19&20\\
21 &22 &23 &24&25
\end{pmatrix}\begin{pmatrix}
21 &22 &23 \\
24 &25 &26 \\
27 &28 &29 \\
\end{pmatrix}\end{align*}
を計算してみることにします。
これはエラーが出ます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3,4,5], [6,7,8,9,10], [11,12,13,14,15], [16,17,18,19,20], [21,22,23,24,25] ]) #行列Bを定義 B=np.matrix([[21,22,23], [24,25,26], [27,28,29] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
結果はエラーが出ます。
|
1 2 3 4 5 6 7 8 9 |
ValueError Traceback (most recent call last) <ipython-input-17-0d4b32b6469a> in <module>() 16 17 #行列の積(AとBの積) ---> 18 C=np.dot(A,B) 19 20 print("行列の積C") ValueError: shapes (5,5) and (3,3) not aligned: 5 (dim 1) != 3 (dim 0) |
「5行5列の行列」と「5行2列の行列」の積
1 &2 &3 &4&5\\
6 &7 &8 &9&10 \\
11 &12 &13 &14&15\\
16 &17 &18 &19&20\\
21 &22 &23 &24&25
\end{pmatrix}\begin{pmatrix}
21 &22 \\
23 &24 \\
25 &26 \\
27 &28 \\
29 &30 \\
\end{pmatrix}\end{align*}
これなら1つ目の行列の”行”と2つ目の行列の”列”の数が合っているので計算ができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3,4,5], [6,7,8,9,10], [11,12,13,14,15], [16,17,18,19,20], [21,22,23,24,25] ]) #行列Bを定義 B=np.matrix([[21,22], [23,24], [25,26], [27,28], [29,20] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
実行してみると、
|
1 2 3 4 5 6 |
行列の積C [[ 395 360] [1020 960] [1645 1560] [2270 2160] [2895 2760]] |
どうやらnp.matrixとしなくても計算してくれる?
行列の積の計算には、計算する行列を
|
1 2 3 4 |
A=np.matrix([[1,2,3], [4,5,6], [7,8,9] ]) |
と書かずに、
|
1 2 3 4 |
A=([[1,2,3], [4,5,6], [7,8,9] ]) |
としてても行列の積は計算してくれるようです。
試しにしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np #行列Aを定義 A=([[1,2,3], [4,5,6], [7,8,9] ]) #行列Bを定義 B=([[11,12,13], [14,15,16], [17,18,19] ]) #行列の積(AとBの積) C=np.dot(A,B) print("行列の積C") print(C) |
実行結果
|
1 2 3 4 |
行列の積C [[ 90 96 102] [216 231 246] [342 366 390]] |
結果は「np.matrix」で行列を作った場合と同じでしたね。
実はmatrixで行列を作成した場合は、A*Bで行列の積を計算できる
後で知ったのですが、行列の積はA*Bと書いても良いみたいです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np #行列Aを定義 A=np.matrix([[1,2,3], [4,5,6], [7,8,9] ]) #行列Bを定義 B=np.matrix([[11,12,13], [14,15,16], [17,18,19] ]) #行列の積(AとBの積) C=A*B print("行列の積C") print(C) |
実行結果
|
1 2 3 4 |
行列の積C [[ 90 96 102] [216 231 246] [342 366 390]] |
Pythonで配列に値を追加
グラフを配列の追加というのをPythonを用いて行います。
配列に値を追加するには「numpyのappend」を使います。
|
1 2 3 4 5 6 7 |
import numpy as np list_a=[1,2,3] list_b=[4,5,6,7,8,9] list_ab=np.append(list_a,list_b) print(list_ab) |
実行結果
|
1 |
[1 2 3 4 5 6 7 8 9] |