こんにちは(@t_kun_kamakiri)。
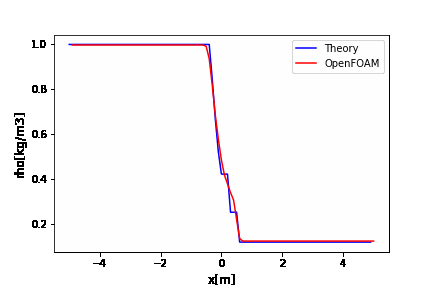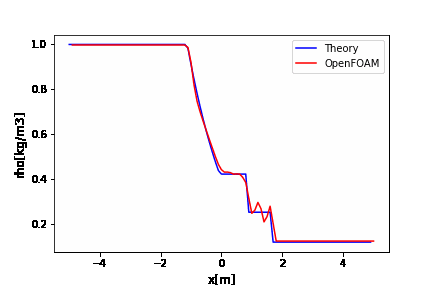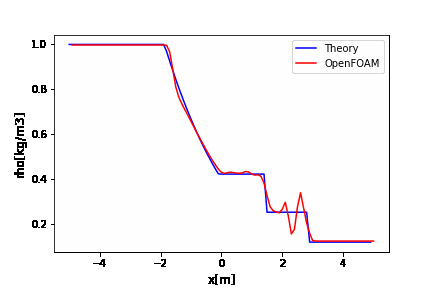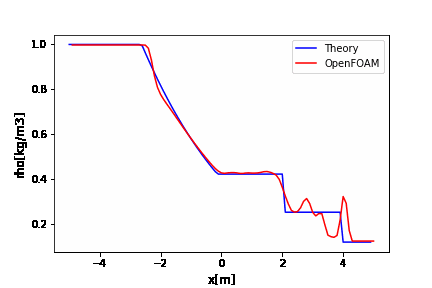
今回は、Pythonを使って「1次元の移流方程式」のアニメーション作成というのやります。
Google Colaboratory上でアニメーション作成を作成する方法は、Jupyter notebookでの方法とじゃっかん違うので調べながらどうにかアニメーション作成までできました。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
☟前回の記事がまだの人はこちらから
1次元移流方程式のアニメーション作成!
1次元移流方程式の差分法
1次元移流方程式の離散化(後退差分)
u^{n+1}_{i}=u^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(u^{n}_{i}-u^{n}_{i-1}\big)
\end{align*}
これをPythonコードで実装します。
まずは、前回の全体のコードを載せておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np import matplotlib.pyplot as plt nx = 41 dx = 2 / (nx-1) nt = 25 dt = .025 c = 1 x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 for n in range(nt): un = u.copy() for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) u_final = u.copy() u_initial = np.ones(nx) u_initial[int(.5 / dx):int(1 / dx + 1)] = 2 plt.plot(x,u_initial,label = 'initial') plt.plot(x,u_final, label = 'final') plt.legend() |
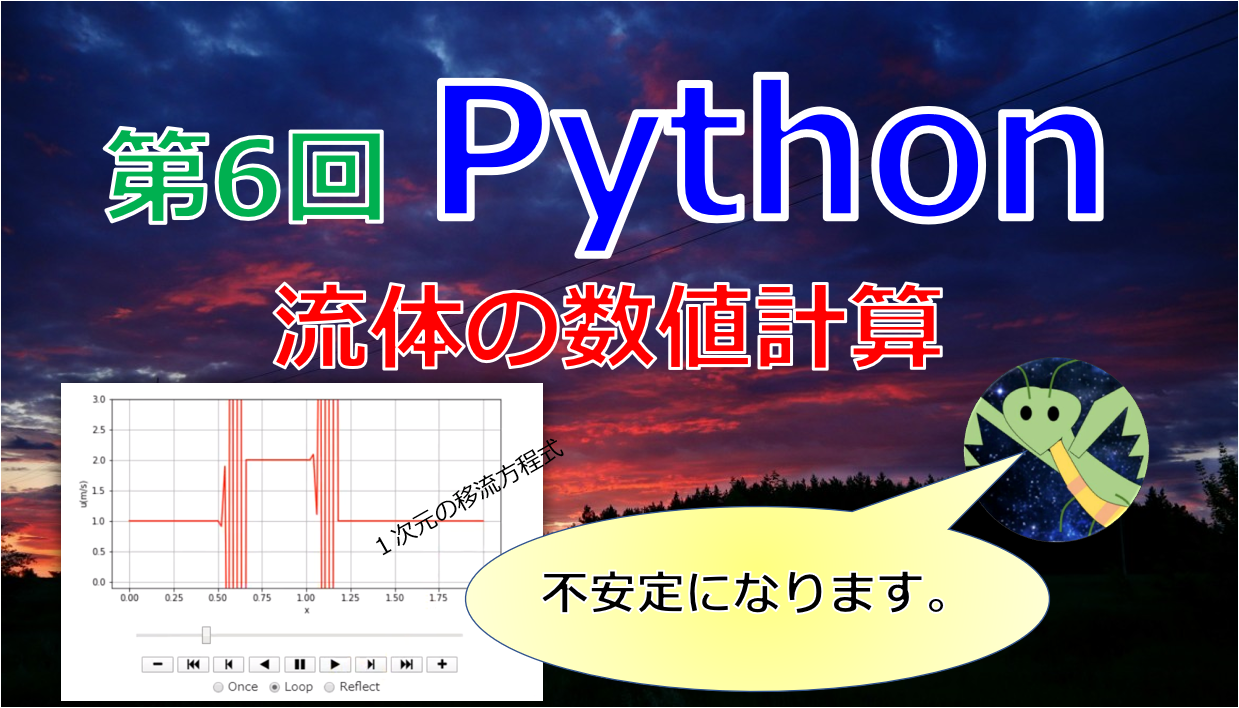
【結果】
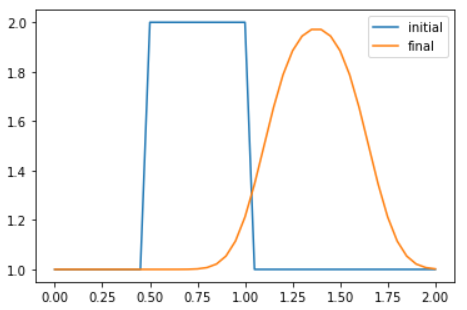
「初期状態のまま形を変えずに+x方向に伝播する解」であるのが移流方程式の厳密解なのに、思いっきり形が変わっていますね(‘ω’)
・・・・というのを前回にやりました。
Matplotlibでアニメーション作成
いきなり全体のコードを載せてもわかりにくそうなので、ひとつひとつコードを解説しながら、後で全体のコードを載せておくことにします。
全体のコードを自身の環境で使用する際は、コピペすれば良いです。
※以下の環境でアニメーション作成方法が異なります。
- Jupyter notebook
- Google Colaboratory
本記事ではGoogle Colaboratoryを使っているため、Google Colaboratoryの解説のみとなりますが、Jupyter notebbokでのアニメーション作成のコードも最後に記載しておきます。
必要なライブラリをインポート
まずは必要なライブラリをインポートしておきます。
アニメーション作成には、「matplotlib.animation.ArtistAnimation」を使います。
【必要なライブラリ】
- Numpy:数値計算用のライブラリ
- Matplotlib:波の形状を2次元プロットして可視化するためのライブラリ
Pythonのコードを書きます。
|
1 2 3 4 |
import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML |
記述間違いがなければエラーが発生しないはずです。
Google Colaboratoryでアニメーションを作成する方法は、Juyter notebookやJupyter labの方法と違っています。
Google ColaboratoryでJupyter notebookと同じように「%matplotlib nbagg」と書いてもアニメーションを表示してくれませんでした。
こちらの記事を参考に必要な記述は何かを調べながらコードを確認して、「JupiterにMatplotlibアニメーションをインタラクティブなJavaScriptウィジェットとして埋め込む」という方法でGoogle Colaboratoryでもアニメーションができました。
初期状態を設定する
こちらは前回と同じ設定にしておきます。
【初期設定】
- 時間刻みは0.25[s]
- 速度c=1[m/s]
空間\(x\)は「0~2(m)」を41分割します。
Pythonのコードを書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
nx = 41 dx = 2 / (nx-1) nt = 25 c = 1 dt = .025 x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 |
ここでも記述間違いがなければエラーなく進むはずです。
初期状態を確認したい場合は、「plt.plot(x,u)」と記述することで確認できますが、アニメーションのスタート時点でも確認できるのでここでは初期状態の確認を行っていません。
アニメーション作成:animation.ArtistAnimation(figオブジェクト, リスト)
アニメーション作成には「matplotlib.animation.ArtistAnimation」を使います。
アニメーション作成の基本的な使い方は、こちらのサイトを見ていくことになりますが、公式サイトはじゃっかんわかりにくいので、ここではわかりやすく簡単な説明をしておきます。
【アニメーション作成】
- fig = plt.figure():描画のサイズなどのオブジェクトを作る
- ims=[]というリストを用意する
ここには、各時刻(ステップ数)のグラフをリストとして格納するようにする - animation.ArtistAnimation(fig, ims)とすればアニメーション作成される
Pythonのコードを書きます。
|
1 2 3 4 5 6 7 8 9 |
fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) |
- fig = plt.figure(figsize=(8,4))で描画のサイズを指定しています(特に何も指定しなくても良いですが、好きな描画のサイズに変更する場合は「figsize=(8,4)」とすれば「横8.0×100=800ピクセル」「縦4.0×100=400ピクセル」に設定できます。)。
- ims=[]で空のリストを用意しておきます。
- im = plt.plot(x,u, “r”)で毎ステップでグラフのオブジェクトを作っています。
- 作ったグラフオブジェクトをims.append(im)としてimsリストに追加してます。
続きのPythonのコードを書きます。
|
1 2 3 4 5 6 7 |
plt.grid() plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) rc('animation', html='jshtml') plt.close() anim |
- 作成した「fig」と「ims」をanimation.ArtistAnimation(fig, ims)に入れることでアニメーション作成ができます。
- anim = animation.ArtistAnimation(fig, ims)として、anim という変数に格納しておきます。
- rc(‘animation’, html=’jshtml’)と書いて「animation.html」をJavascriptで動かしている(?あまりよくわかっていない)
- 「plt.close()」としてグラフのオブジェクトを閉じておきます。
※あまりよくわかっていないですが、「plt.close()」でグラフオブジェクトを閉じておかないと、以下のように動画と何も表示されていないグラフの枠だけができてしまいます。
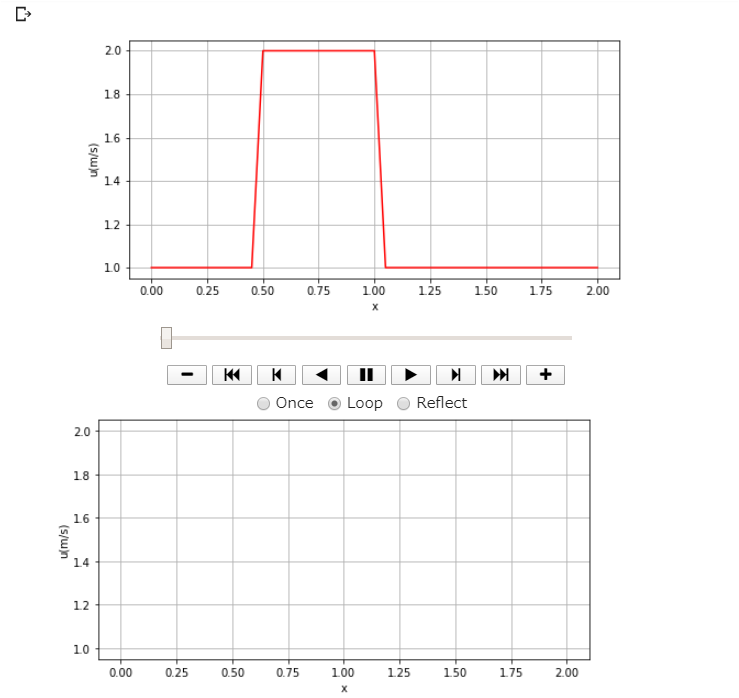
- 最後に変数「anim」を出力すればアニメーションが表示されます(^^)/
【結果】
やっぱり、「初期状態のまま形を変えずに+x方向に伝播する解」であるのが移流方程式の厳密解なのに、思いっきり形が変わっていますね(‘ω’)
全体のコード
全体のコードを載せておきますので、コピペすることで移流方程式の数値計算結果のアニメーション作成ができます。
Google Colaboratory
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML nx = 41 dx = 2 / (nx-1) nt = 25 c = 1 dt = .025 x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) plt.grid() plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) rc('animation', html='jshtml') plt.close() anim |
Jupyter notebook
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
%matplotlib nbagg import numpy as np import matplotlib.pyplot as plt from matplotlib import animation nx = 41 dx = 2 / (nx-1) nt = 25 dt = .025 c = 1 x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) plt.grid() plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) |
|
1 2 3 |
if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) |
のif文の中身は動画を作成するためのグラフを作成する処理を書
「if (nt%1==0):」 であれば、毎ステップグラフを作成するようにしているので、
- 「if (nt%10==0):」 とすると、10ステップごとにグラフを作成するようになります。
- 「if (nt%20==0):」 とすると、20ステップごとにグラフを作成するようになります。
そうすると、アニメーションの容量を削減できます(
数字を変えて試してみてください。
まとめ
今回は、「1次元の移流方程式」の数値計算とアニメーション作成をPythonで実装しました。
次回はじゃっかん数値計算の闇の部分に踏み込みます。
- クーラン条件
- 差分法の種類(後退差分、前進差分、中心差分)
によって解の安定性が変わってくるというのを確認したいと思います。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
(本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません)
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと!!って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学1年生で偏微分を学んだ方にとってはちょうどよい参考書です。