こんにちは(@t_kun_kamakiri)。
本日は、「1次元のバーガース方程式」の非線形性のお話をします。
前回の記事までで、「1次元の移流方程式」「1次元の拡散方程式」「1次元バーガース方程式」をPythonで実装するというのをやりました。
ちょっとずつナビエストークス方程式の実装に近づいています!
「とりあえず、Pythonを使ってナビエストークス方程式を解いてみたい!」という方には、この記事シリーズはとても勉強になるのではないかと思います。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
本記事シリーズの最終目標は、ナビエストークス方程式をPythonで実装することですが、いきなりナビエストークス方程式を実装するのは難しいので各項の意味を確認しながら進めていきたいと思います。
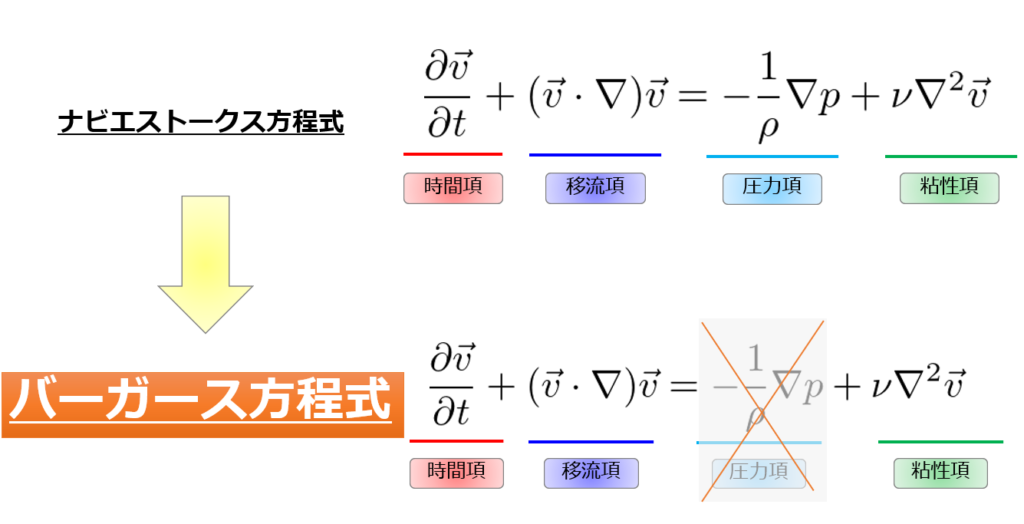
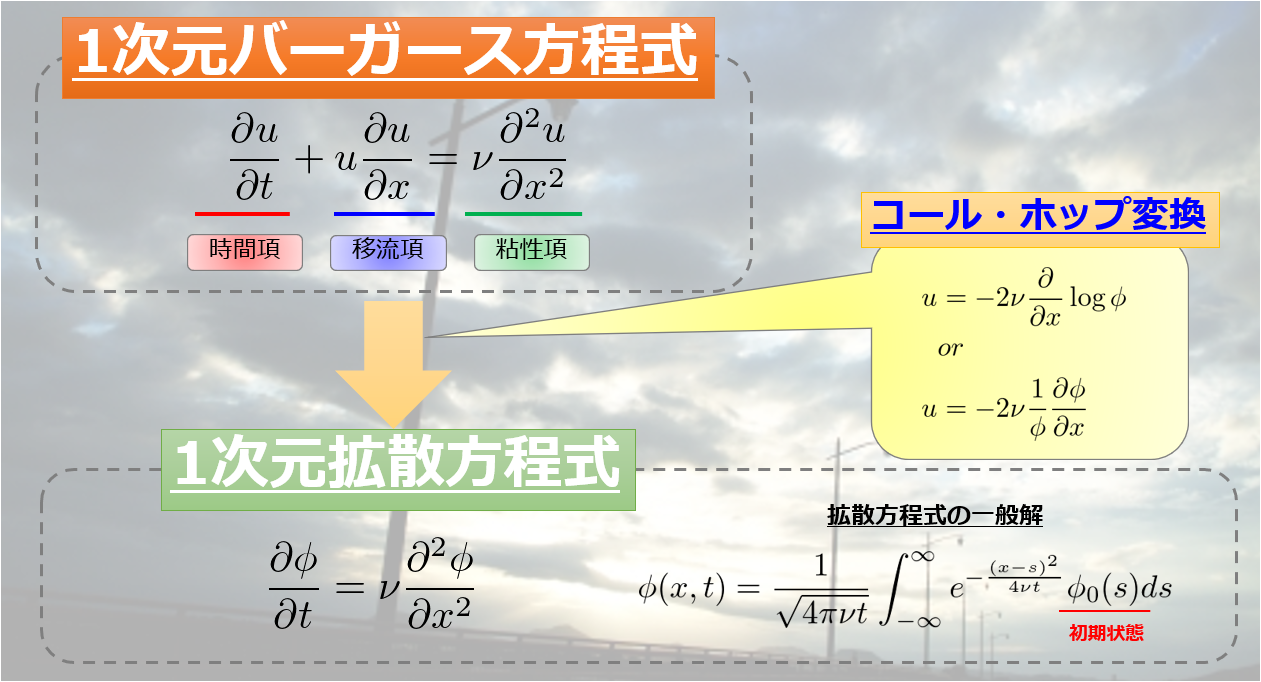
バーガース方程式とは
バーガース方程式は、ナビエストークス方程式において移流項が圧力項より十分大きい場合\(|(\boldsymbol{u}\cdot\nabla)\boldsymbol{u}|>>|\frac{1}{\rho}\nabla p|\)において近似される以下の式で記述されます。
1次元のバーガース方程式
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2} \tag{1}
\end{align*}
圧力項より移流項の方が十分大きいとは、例えば流速がものすごく大きい極音速領域や流速の空間変動が急激な場合などが考えられます。
ここからいくつかバーガース方程式の特徴を列挙していきます。
- 非線形性がある
- コール・ホッフ変換によって拡散方程式になる
- 衝撃波
本記事のメインの内容は「バーガース方程式の非線形性」についてです。
非線形性が意味するところを簡単に説明しようと思います。
非線形性がある
バーガース方程式における「非線形性の項」というのは、(1)式の左辺第二項\(u\frac{\partial u}{\partial x}\)のことです。
今から求めたい\(u\)が微分があるものの\(u\)自身での掛け算が存在する項が非線形項と呼ばれています。
非線形性があることによる効果は、一言でいうと「異なる波数間の相互作用が存在する」という事です。
これにはフーリエ変換をすることで確かめることで理解が深まります。
フーリエ変換は波数を変数にした空間(一般にはフーリエ空間と呼ばれる)に移る変換のことですが、そこからわかることも多くあります。
「フーリエ変換って何?」という人のために、少しだけフーリエ変換の復習をします。
フーリエ変換の復習
1次元のバーガース方程式
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}= \nu \frac{\partial^2 u}{\partial x^2} \tag{1}
\end{align*}
この解\(u(x,t)\)を逆フーリエ変換すると以下のようになります。
u(x,t)=\int^{\infty}_{-\infty}\tilde{u}(k,t)e^{ikx}dk\tag{2}
\end{align*}
\(k\):波数
フーリエ変換とは、異なる波数\(k\)の波\(e^{ikx}\)を重み\(\tilde{u}(k,t)\)で重ね合わせであると理解できます。
(2)式のフーリエ変換は、
\tilde{u}(k,t)=\frac{1}{2\pi}\int^{\infty}_{-\infty}u(x,t)e^{-ikx}dx\tag{3}
\end{align*}
となります。
以下の3つのポイントはよく使うので覚えておくと良いでしょう。
フーリエ変換(3)式の導出は、
- (2)式の両辺に\(e^{-ik^{\prime}x}\)をかけて\(x\)で積分を行う。
- \(\delta(x)=\frac{1}{2\pi}\int^{\infty}_{-\infty}e^{ikx}dk\)を用いる。
- \(f(a)=\int^{\infty}_{-\infty}f(x-a)\delta(x)dx\)を用いる。
1.(2)式の両辺に\(e^{-ik^{\prime}x}\)をかけて\(x\)で積分を行う。
\int u(x,t)e^{-ik^{\prime}x}dx=\int\int\tilde{u}(k,t)e^{i(k-k^{\prime})x}dkdx
\end{align*}
※積分区間は省略しました。
2.\(\delta(x)=\frac{1}{2\pi}\int^{\infty}_{-\infty}e^{ikx}dk\)を用いる。
右辺の\(x\)積分を実行します。
以下のように、わかりやすく括弧でくくっています。
(右辺) &=& \int\tilde{u}(k,t)\bigg(\int e^{i(k-k^{\prime})x}dx\bigg)dk\\
&=&\int\tilde{u}(k,t)\bigg(2\pi\delta(k-k^{\prime})\bigg)dk
\end{align*}
3.\(f(a)=\int^{\infty}_{-\infty}f(x-a)\delta(x)dx\)を用いる。
最後は右辺を\(k\)で積分すればフーリエ変換が終了です。
(右辺) &=2\pi\int\tilde{u}(k,t)\delta(k-k^{\prime})dk\\
&=2\pi\tilde{u}(k,t)
\end{align*}
「1~3」を経て、(3)式となります。
\tilde{u}(k,t)=\frac{1}{2\pi}\int^{\infty}_{-\infty}u(x,t)e^{-ikx}dx\tag{3}
\end{align*}
参考書によっては、係数の\(\frac{1}{2\pi}\)がなかったりしますがフーリエ変換の係数は本質的な部分ではないのであまり気にしなくても良いです。
逆フーリエ変換に\(\frac{1}{2\pi}\)がない分、フーリエ変換の方にあったり・・・係数が\(\frac{1}{\sqrt{2\pi}}\)だったり説明によって様々です。
バーガース方程式のフーリエ変換
では、(1)式のバーガース方程式をフーリエ変換します。
いきなりすると混乱するので、各項ひとつひとつ見ていきます(面倒な方は飛ばしてください)。
それには先ほどのポイント1~3を使います。
左辺第一項(時間変化の項)
\frac{\partial u(x,t)}{\partial t}=\int\frac{\partial \tilde{u}(k,t)}{\partial t}e^{ikx}dk
\end{align*}
これはわかりやすいですよね。
ポイント1~3を使って・・・
&\int\frac{\partial u(x,t)}{\partial t}e^{ikx}e^{-ik^{\prime\prime}x}dx=\int\int\frac{\partial \tilde{u}(k,t)}{\partial t}e^{i(k-k^{\prime\prime})x}dxdk^{\prime\prime}\\
& \underset{xで積分} =2\pi\int\frac{\partial \tilde{u}(k,t)}{\partial t}\delta(k-k^{\prime\prime})dk^{\prime\prime}\\
& \underset{kで積分\\(k=k^{”})} =2\pi\frac{\partial \tilde{u}(k,t)}{\partial t}\tag{4}
\end{align*}
こんなノリでどんどん計算していきます。
左辺第二項(非線形の項)
こいつがちょっとやっかいです。
u\frac{\partial u}{\partial x}=i\int\int \big(\tilde{u}(k,t)k^{\prime}\big)\tilde{u}(k^{\prime},t)e^{i(k+k^{\prime})x}dkdk^{\prime}
\end{align*}
ポイント1~3を使って・・・
&i\int\int\int \big(\tilde{u}(k,t)k^{\prime}\big)\tilde{u}(k^{\prime},t)e^{i(k+k^{\prime}-k^{\prime\prime})x}dkdk^{\prime}dx\\
&\underset{xで積分}=2\pi\int\int \big(\tilde{u}(k,t)k^{\prime}\big)\tilde{u}(k^{\prime},t)\delta(k+k^{\prime}-k^{\prime\prime})dkdk^{\prime}\\
&\underset{kで積分\\(k=k^{”}-k^{‘})}=2\pi\int\big(\tilde{u}(k-k^{\prime},t)k^{\prime}\big)\tilde{u}(k^{\prime},t)dk^{\prime}\tag{5}
\end{align*}
ちょっと複雑なままですがこれ以上は何もできないのでこのまま進みます。
右辺第一項(拡散項)
\nu \frac{\partial^2 u}{\partial x^2}=-\nu\int k^2\tilde{u}(k,t)e^{ikx}dk
\end{align*}
ポイント1~3を使って・・・
&-\nu \int\int k^2\tilde{u}(k,t)e^{ikx}e^{-ik^{\prime\prime}x}dx\\
&-\nu \int\int k^2\tilde{u}(k,t)e^{i(k-k^{\prime\prime})x}dxdk^{\prime\prime}\\
&\underset{xで積分}=-\nu \int k^2\tilde{u}(k,t)\delta(k-k^{\prime\prime})dk^{\prime\prime}\\
&\underset{kで積分\\(k=k^{”})}=-\nu k^2\tilde{u}(k,t)\tag{6}
\end{align*}
以上でフーリエ変換が終了しました。
上記の手続きにより、フーリエ空間(波数空間)での偏微分方程式が得られたことになりますね。
(4)(5)(6)をつなげておきます。
\frac{\partial \tilde{u}(k,t)}{\partial t}&=\int k^{\prime}\tilde{u}(k-k^{\prime},t)\tilde{u}(k^{\prime},t)dk^{\prime}-\nu k^2 \tilde{u}(k,t)\tag{7}
\end{align*}
フーリエ変換することにより以下の2点がわかります。
- フーリエ空間(波数空間)ではもともと微分だった項が波数との掛け算になっている
- 非線形項は異なる波数同士の相互作用がある
フーリエ変換を使うことで非線形項の意味が分かるようになると同時に、フーリエ空間に変換することのメリットもわかるでしょう(^^)/
1.フーリエ空間(波数空間)ではもともと微分だった項が波数との掛け算になっている
「1」については、計算してみればわかるのですが、例えば
- \(\nabla f(\boldsymbol{x})\)⇒\(\boldsymbol{k}\tilde{f}(\boldsymbol{k})\)
- \(\nabla\cdot \boldsymbol{v}(\boldsymbol{x})\)⇒\(\boldsymbol{k}\cdot\tilde{\boldsymbol{v}}(\boldsymbol{k})\)
- \(\nabla \times \boldsymbol{v}(\boldsymbol{x})\)⇒\(\boldsymbol{k}\times\tilde{\boldsymbol{v}}(\boldsymbol{k})\)
のように微分の項は、フーリエ変換後には掛け算になっています。
このことは例えば数値計算をする場合においては、微分は差分によって必ず誤差が生じるのですがフーリエ変換ではその誤差がありません。
ゆえに精度の良い数値計算方法と言えます。
これをスペクトル法と言います。
が・・・
一見万能に思えるスペクトル法ですが、数値計算は有限な空間でしか行うことができないので数値計算の際はフーリエ変換ではなく、フーリエ級数展開をする必要があり、フーリエ級数展開は周期性のある場合にしか適用できないのでスペクトル法は計算ができる制限があります。(例えば、「周期境界条件」とか)。
2.非線形項は異なる波数同士の相互作用がある
「2」の異なる波数間で相互作用があるというのが、この非線形項の特徴のひとつです。
\tilde{u}(k-k^{\prime},t)\tilde{u}(k^{\prime},t)
\end{align*}
は、畳み込みの形になっています。
※(7)式は\(k\)の掛け算もありますが今は省いています。
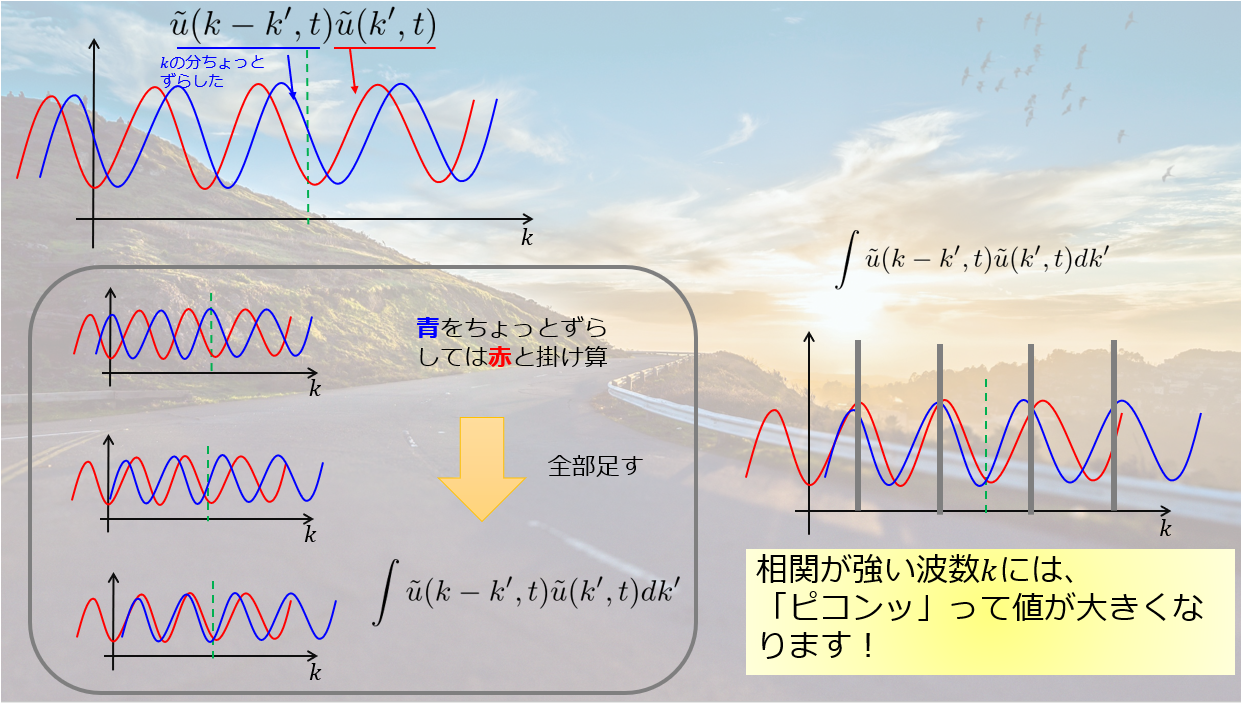
畳み込み積分は、変数(今の場合は波数\(k\))に対してどれだけ相関があるかという量を表しています。
以下の絵のように、\(\tilde{u}(k^{\prime},t)\)に対して\(波数k\)だけずらした\(\tilde{u}(k-k^{\prime},t)\)の掛け算を考え、\(波数k\)をずらしては\(k^{\prime}\)で積分・・・\(波数k\)をずらしては\(k^{\prime}\)で積・・・としています。
例えば、以下のような周期関数の場合には周期に応じて畳み込み積分の値は大きくなります。
つまり、相関が強い位置の波数\(k\)で大きな値をとります。
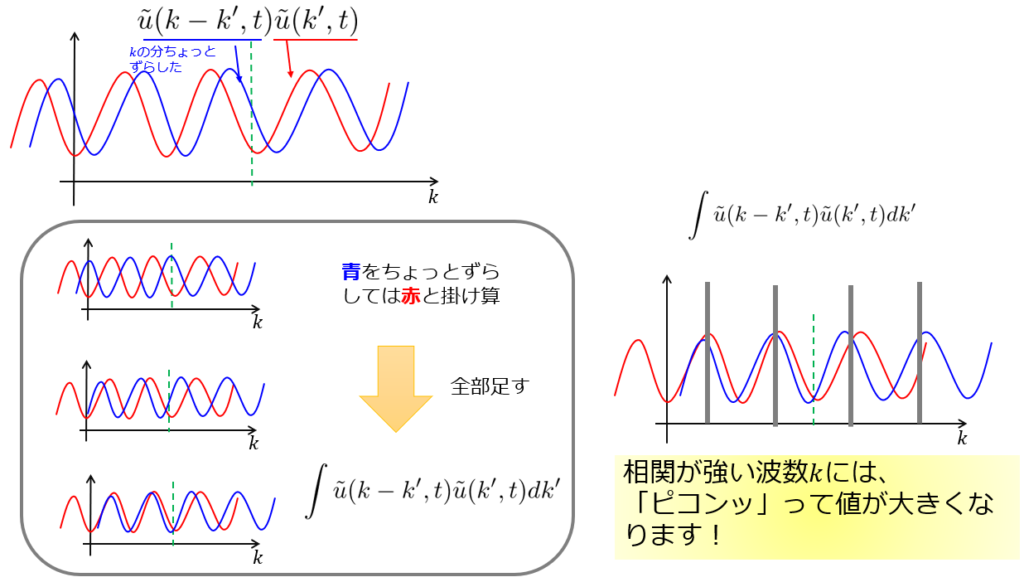

このように、畳み込み積分には自身の波数\(k\)とどれだけ相関があるかという意味を持つ量です。
(自己相関関数とも呼ばれています。)
非線形項は異なる波数でも、相関が強い波数同士は共感しあって大きな値を持つようになるんだなって思ってもらえれば良いかと思います。
これって、線形項には異なる波数間での相互作用はないので非線形項の特徴のひとつですよね。
線形方程式の場合には、例えば(1)式のバーガース方程式に非線形項がなければ線形項のみになるので、異なる波数同士は互いに独立で方程式を満たします。
つまり、線形項においては異なる波数同士は相互作用を及ぼし合うことはありません。
しかし、非線形項には異なる波数間での相互作用があるために、非線形項が大きいと様々な波数を作り出すため乱れが生じます・・・・
言葉で説明するとこんな感じになりますかね。。
いかに非線形項がめんどくさいかわかってもらえれば良いですが。
まとめ
今回は、バーガース方程式の非線形性についてのお話をしました。
ナビエストークス方程式がいかに複雑な現象を表している偏微分方程式かというのが少し理解できたのではないかと思います。
フーリエ変換も少々計算が面倒ですが、紙に書きながら式を追えば理解できると思いますので、億劫がらずに計算してみてください(‘◇’)ゞ
☟以下の書籍で詳しく書かれているので是非お読みください(‘◇’)ゞ