こんにちは（@t_kun_kamakiri）
OpenFOAMの衝撃波菅内の解析と厳密解との比較を行います。
本記事では衝撃波管内の厳密解についてのプログラムを載せておきます。
コードは自分のメモ用としてPythonでべた書きしています。
後日OpenFOAMのチュートリアルと比較するためのものです。
コードの実行にはjupyter labで順番に実行していきます。
衝撃波官
- 1次元波動のショックチューブ（衝撃波管）
- 20世紀後半に研究したゲーリー A. ソッド(Gary A. Sod)にちなんでsod shock tubeと呼ばれる
- 1次元の非粘性圧縮方程式（オイラー方程式）と理想気体を仮定したの厳密解があり、数値流体の精度や安定性の評価に使われる
- OpenFOAMにはrhoCentralFoamとsonicFoamにチュートリアルがある
- 非粘性の圧縮流れの方程式（1次元オイラー方程式）で記述
- 衝撃波前後でランキン・ユゴニオの関係式と理想気体の断熱過程の式より厳密解が求まる
必要なライブラリと初期状態
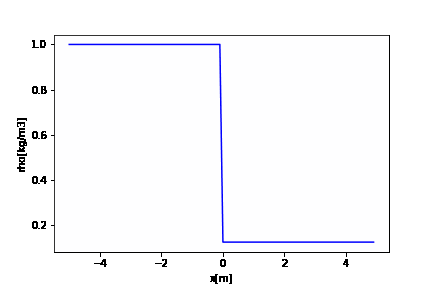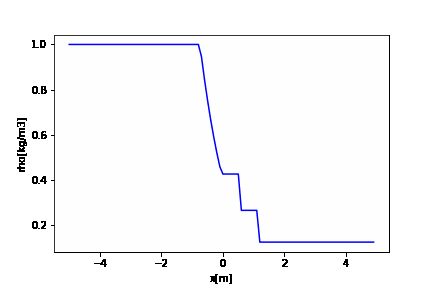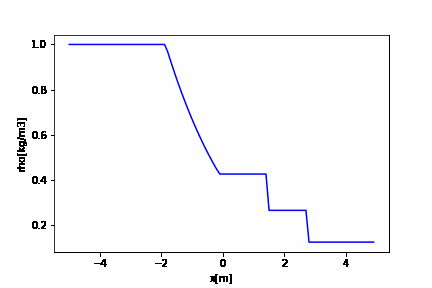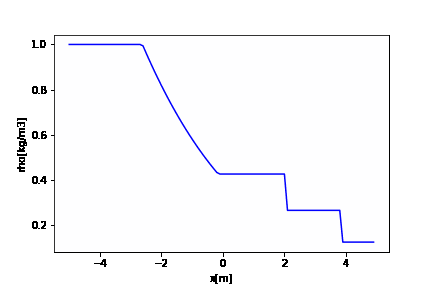
まずは適当に初期状態を与えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import numpy as np import pandas as pd import numpy as np import matplotlib.pyplot as plt gamma = 1.4 XL = -5.0 XR = 5.0 tstop = 0.007 dt = 1e-3 t = 0 i_max = 100 dx = (XR - XL) / i_max x = np.zeros(i_max) rhoe = np.zeros(i_max) pe = np.zeros(i_max) ue = np.zeros(i_max) tempe = np.zeros(i_max) x0 = 0 #初期区切り位置 R = 8.31446262 #[mol/J K] MW = 28.96/1000 #[kg/mil] Rmw = R/MW # 初期状態1 p1 = 10000#0.1 T1 = 278.746 rho1 = p1/(Rmw*T1)#0.12 u1 = 0.0 c1 = np.sqrt(gamma * p1 / rho1) if t == 0: print(f"初期状態 rho1={rho1}") # 初期状態5 T5 = 348.432 p5 = 100000#1.0 rho5 = p5/(Rmw*T5)#1.0 u5 = 0.0 c5 = np.sqrt(gamma * p5 / rho5) if t == 0: print(f"初期状態 rho5={rho5}") for i in range(i_max): x[i] = XL + dx*i # セル境界の座標 # 高圧、高温 if x[i] < x0: rhoe[i] = rho5 pe[i] = p5 ue[i] = u5 tempe[i] = pe[i]/(rhoe[i]*Rmw) # 低圧、低温 else: rhoe[i] = rho1 pe[i] = p1 ue[i] = u1 #温度の計算 tempe[i] = pe[i]/(rhoe[i]*Rmw) |
反復計算用の関数
以下は$\frac{p_{2}}{p_{1}}=p_{21}$を求めるための関数です。
式で書くと
\begin{align*}
\frac{p_{2}}{p_{1}}=\frac{p_{R}}{p_{L}}\bigg(\,\,\,1+ \frac{\gamma-1}{2c_{L}}\bigg(u_{L}-u_{R}-\frac{c_{R}(\frac{p_{2}}{p_{1}}-1)}{\gamma\sqrt{\frac{\gamma+1}{2\gamma}}(\frac{p_{2}}{p_{1}}-1)+1}\bigg)\,\,\,\bigg)^{\frac{2\gamma}{\gamma-1}}
\end{align*}
と少々複雑です。
\frac{p_{2}}{p_{1}}=\frac{p_{R}}{p_{L}}\bigg(\,\,\,1+ \frac{\gamma-1}{2c_{L}}\bigg(u_{L}-u_{R}-\frac{c_{R}(\frac{p_{2}}{p_{1}}-1)}{\gamma\sqrt{\frac{\gamma+1}{2\gamma}}(\frac{p_{2}}{p_{1}}-1)+1}\bigg)\,\,\,\bigg)^{\frac{2\gamma}{\gamma-1}}
\end{align*}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# p21を求めるための関数 def F(p21, p1, p5, rho1, rho5, u1, u5): # c1, c5, w c1 = np.sqrt(gamma*p1/rho1) c5 = np.sqrt(gamma*p5/rho5) w = p5/ p1*( 1.0 + (gamma - 1)/ c5 / 2.0 * (u5 - u1 - c1 / gamma * (p21 - 1.0) * ( (gamma + 1.0) / (2.0*gamma) * (p21 - 1.0) + 1.0 )**(-1.0 / 2.0) ) )**(2 * gamma / (gamma - 1)) - p21 return w |
厳密解を解くための関数
こちらが厳密解を解くためのプログラム部分です。
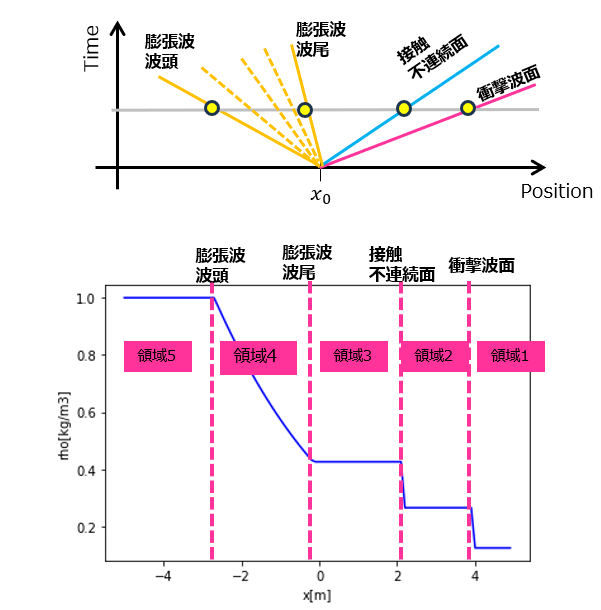
- 領域1 $ x>x_{0}+V_{s}t$
$\rho_{1}=\rho_{R}$, $p_{1}=p_{R}$, $u_{1}=u_{R}$
衝撃波速度$ V_{s}=u_{1}+c_{1}\sqrt{\frac{\gamma + 1}{2\gamma}\big(\frac{p_{2}}{p_{1}-1}+1\big)}$ - 領域2 $ x_{0}+V_{c}t < x \leq x_{0}+V_{s}t$
衝撃波の前後でランキン・ユゴニオの関係式より、$\frac{\rho_{2}}{\rho_{R}}=\frac{\frac{p_{2}}{p_{R}}+\frac{\gamma-1}{\gamma+1}}{\frac{\gamma-1}{\gamma+1}\frac{p_{2}}{p_{R}}+1}$
$u_{2}=u_{R}+\frac{c_{R}\big(\frac{p_{2}}{p_{R}}-1\big)}{\sqrt{\frac{\gamma}{2}\big(\gamma-1+\frac{p_{2}}{p_{R}}(\gamma+1)\big)}}$ - 領域3 $x_{0}+V_{rt}t < x \leq x_{0}+V_{c}t$ $(V_{rt}=u_{2}-\frac{\gamma-1}{2}(u_{L}-u_{2})+c_{L})=u_{3}-c_{3}$
等エントロピー過程よりポアソンの関係式を使って、$p_{3}\rho_{3}^{\gamma}=p_{L}\rho_{L}^{\gamma}$,
流速と圧力は変化がないので$u_{3}=u_{2}=V_{c}$, $p_{3}=p_{2}$
$c_{3}=\sqrt{\frac{\gamma p_{3}}{\rho_{3}}}=\frac{\gamma-1}{2}(u_{L}-u_{3})+c_{L}$ - 領域4 $x_{0}+V_{rh}t < x \leq x_{0}+V_{rt}t$
流速$u_{4}=\frac{2}{\gamma+1}\big(\frac{x-x_{0}}{t}+c_{L}+\frac{\gamma-1}{2}u_{L}\big)$
音速$c_{4}=c_{L}-\frac{\gamma-1}{2}(u_{4}-u_{L})$
等エントロピー過程よりポアソンの関係式を使って、$p_{4}\rho_{4}^{\gamma}=p_{L}\rho_{L}^{\gamma}$ or $p_{4}c_{4}^{\frac{2\gamma}{\gamma-1}}=p_{L}c_{L}^{\frac{2\gamma}{\gamma-1}}$ - 領域5 $x\leq x_{0}+V_{rh}t$
$p_{5}=p_{L}$, $u_{5}=u_{L}$, $\rho_{5}=\rho_{L}$
まずは$\frac{p_{2}}{p_{1}}=p_{21}$を求めるための反復計算を行っています。
\begin{align*}
\frac{p_{2}}{p_{1}}=\frac{p_{R}}{p_{L}}\bigg(\,\,\,1+ \frac{\gamma-1}{2c_{L}}\bigg(u_{L}-u_{R}-\frac{c_{R}(\frac{p_{2}}{p_{1}}-1)}{\gamma\sqrt{\frac{\gamma+1}{2\gamma}}(\frac{p_{2}}{p_{1}}-1)+1}\bigg)\,\,\,\bigg)^{\frac{2\gamma}{\gamma-1}}
\end{align*}
は「F(p21, p1, p5, rho1, rho5, u1, u5)」の関数から求めています。
\frac{p_{2}}{p_{1}}=\frac{p_{R}}{p_{L}}\bigg(\,\,\,1+ \frac{\gamma-1}{2c_{L}}\bigg(u_{L}-u_{R}-\frac{c_{R}(\frac{p_{2}}{p_{1}}-1)}{\gamma\sqrt{\frac{\gamma+1}{2\gamma}}(\frac{p_{2}}{p_{1}}-1)+1}\bigg)\,\,\,\bigg)^{\frac{2\gamma}{\gamma-1}}
\end{align*}
※理想気体の状態方程式から、温度と密度と圧力は$p=\rho R_{MW} T$
ただし、$R_{MW}$は気体定数$R=8.31$[J/k mol]とモル質量$MW=28.9$[mol](空気のモル質量)から、$R_{MW}=\frac{R}{MW}$で計算される値であることに注意
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
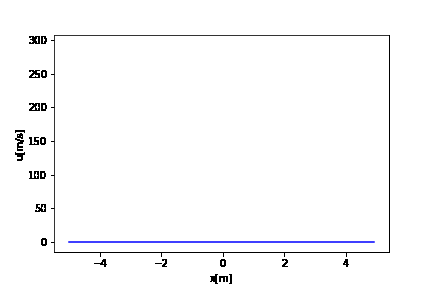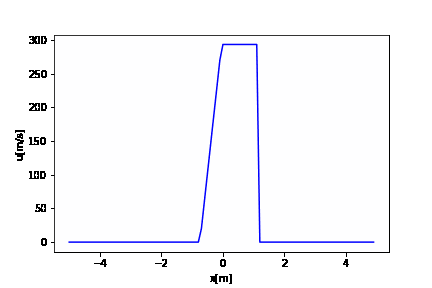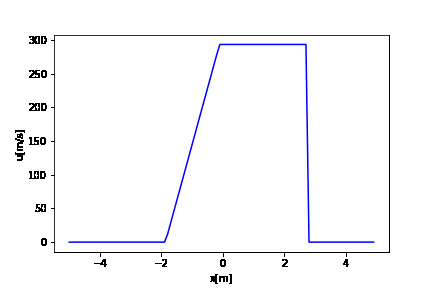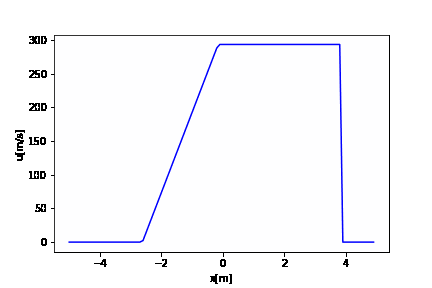
# 厳密解の時間発展 def exact_solution(t): #Secant反復法により、衝撃波前後の圧力ジャンプを求める p21 = p1 / p5 pm = p21 + 0.01 pmm = pm + 0.01 fmm = F(pm, p1, p5, rho1, rho5, u1, u5) itmax = 20 # 反復回数の上限 it = 0 eps = 1.e-5 # 収束判定条件 error = 1 while error > eps: it += 1 fm = F(p21, p1, p5, rho1, rho5, u1, u5) df = fm - fmm p21 = p21 - (p21 - pmm) * fm / (df + 1.0e-8 * df / (abs(df) + 1.0e-8)) error = abs(p21 - pm) / pm pmm = pm pm = p21 fmm = fm #printf("反復回数=%d,p21=%f\n",it, p21); if (it >= itmax): break #print(f"p21={p21}") #領域2の物理量を計算する rho2 = rho1 * (p21 + (gamma - 1) / (gamma + 1))/((gamma - 1) * p21 / (gamma + 1) + 1) u2 = u1 + c1 * np.sqrt(2.0 / gamma) * (p21 - 1) /np.sqrt(gamma - 1 + p21 * (gamma + 1)) p2 = p21 * p1 #print(f"rho2={rho2},u2={u2},p2={p2}") #領域3の物理量を計算する u3 = u2 p3 = p2 rho3 = rho5 * pow(p3 / p5, 1.0 / gamma) c3 = np.sqrt(gamma * p3 / rho3) #print(f"rho3={rho3},u3={u3},p3={p3}") # 各波の速度を計算する Vs = u1 + c1 * np.sqrt((gamma + 1) / (2. * gamma) * (p21 - 1) + 1) # 衝撃波 Vc = u3 # 接触不連続 Vrt = u3 - c3 # 膨張波末端の速度 Vrh = u5 - c5 # 膨張波先端の速度 #print(f"Vs={Vs},Vc={Vc},Vrt={Vrt},,Vrh={Vrh}") # # t時刻における波の位置を計算する xs = x0 + Vs * t # 衝撃波 xc = x0 + Vc * t # 接触不連続 xrt = x0 + Vrt * t # 膨張波末端の速度 xrh = x0 + Vrh * t # 膨張波先端の速度 #print(f"xs={xs},xc={xc},xrt={xrt},xrh={xrh}") # 計算格子に解を与える for i in range(i_max): # 領域5 if x[i] < xrh: rhoe[i] = rho5 pe[i] = p5 ue[i] = u5 # 領域4 elif x[i] <= xrt: ue[i] = 2. / (gamma + 1) * (0.5 * (gamma - 1) * u5 + c5 + (x[i] - x0) / t) c4 = c5 - 0.5 * (gamma - 1) * (ue[i] - u5) pe[i] = p5 * pow(c4 / c5, (2. * gamma / (gamma - 1))) rhoe[i] = rho5 * pow(pe[i] / p5, 1.0 / gamma) # 領域3 elif (x[i] < xc): rhoe[i] = rho3 pe[i] = p3 ue[i] = u3 # 領域2 elif (x[i] < xs): rhoe[i] = rho2 pe[i] = p2 ue[i] = u2 # 領域1 else: rhoe[i] = rho1 pe[i] = p1 ue[i] = u1 # 温度の計算 tempe = pe/(rhoe*Rmw) return rhoe, pe, ue, tempe |
時間発展の計算
座標に対する物理量をリストに格納しています。
さらに、各時刻の物理場（リスト）をリストに入れています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 初期化 rhoet = [rhoe] pet = [pe] uet = [ue] tempet = [tempe] t = 0 while t <= tstop: t = t + dt rhoe = np.zeros(i_max) pe = np.zeros(i_max) ue = np.zeros(i_max) rhoe, pe, ue, tempe = exact_solution(t) rhoet.append(rhoe) pet.append(pe) uet.append(ue) tempet.append(tempe) |
アニメーションの作成
まずは密度のアニメーション
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
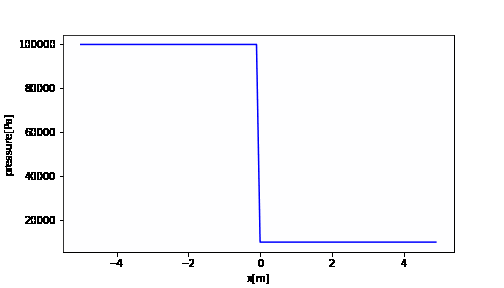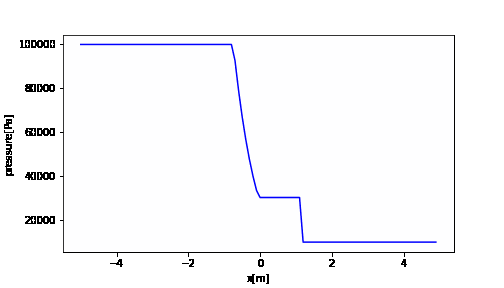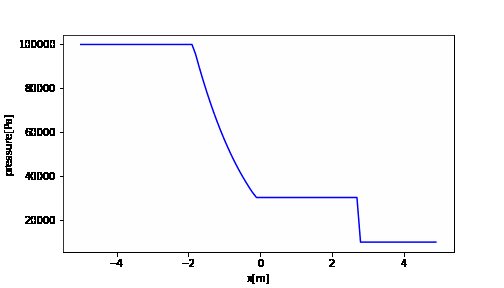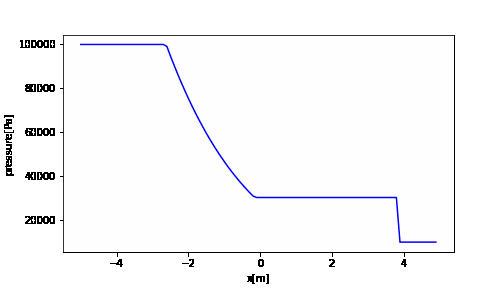
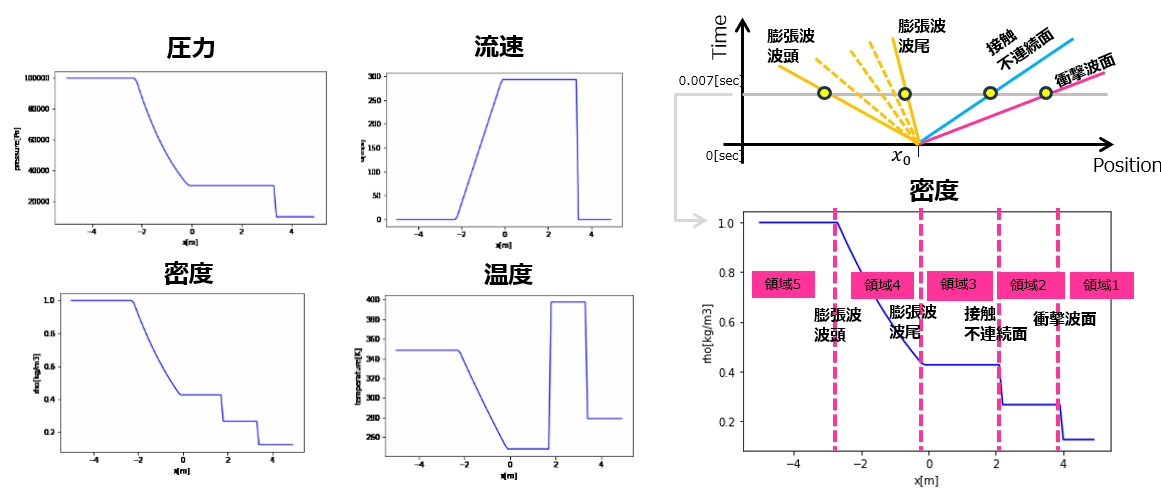
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure() x = np.arange(XL, XR, dx) # アニメーション ims_rho = [] it = 0 t = 0 while t <= tstop: im_rho = plt.plot(x, rhoet[it], "b") ims_rho.append(im_rho) plt.xlabel("x[m]") plt.ylabel("rho[kg/m3]") t = t + dt it += 1 ani_rho = animation.ArtistAnimation(fig, ims_rho, interval=1) ani_rho.save('rho.gif', writer='pillow') |
続いて流速のアニメーション
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure() x = np.arange(XL, XR, dx) # アニメーション ims_u = [] it = 0 t = 0 while t <= tstop: im_u = plt.plot(x, uet[it], "b") ims_u.append(im_u) plt.xlabel("x[m]") plt.ylabel("u[m/s]") t = t + dt it += 1 ani_u = animation.ArtistAnimation(fig, ims_u, interval=1) ani_u.save('u.gif', writer='pillow') |
続いて圧力のアニメーション
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure(figsize=(7,4)) x = np.arange(XL, XR, dx) # アニメーション ims_p = [] it = 0 t = 0 while t <= tstop: im_p = plt.plot(x, pet[it], "b") plt.xlabel("x[m]") plt.ylabel("pressure[Pa]") ims_p.append(im_p) t = t + dt it += 1 ani_p = animation.ArtistAnimation(fig, ims_p, interval=1) ani_p.save('pe.gif', writer='pillow') |
続いて温度のアニメーション
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
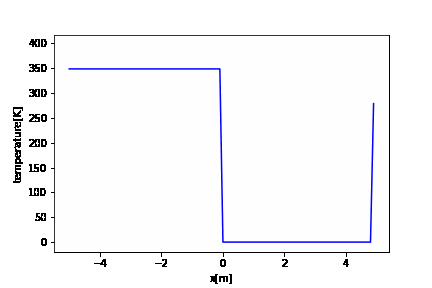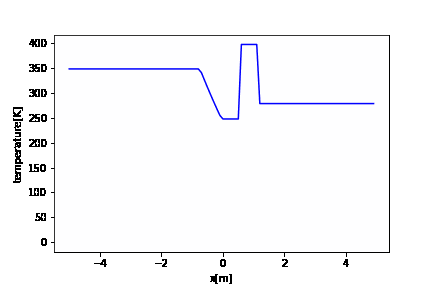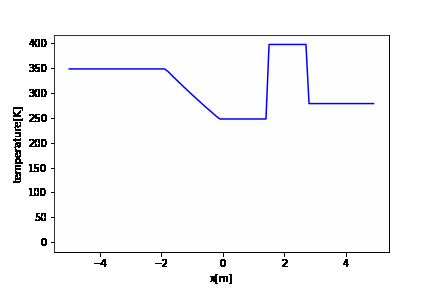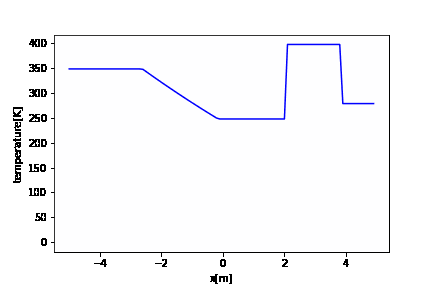
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation fig = plt.figure() x = np.arange(XL, XR, dx) # アニメーション ims_t = [] it = 0 t = 0 while t <= tstop: im_t = plt.plot(x, tempet[it], "b") plt.xlabel("x[m]") plt.ylabel("temperature[K]") ims_t.append(im_t) t = t + dt it += 1 ani_t = animation.ArtistAnimation(fig, ims_t, interval=1) ani_t.save('tempe.gif', writer='pillow') |
各時刻のcsvデータを出力
ついでに各時刻のcsvデータも出力しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
it = 0 t = 0 cols=["#x[m]", "temp[K]", "p[Pa]", "rho[kg/m3]", "u[m/s]"] while t <= tstop: time = round(t,4) if time>0 and time%0.0010 == 0: df = pd.DataFrame([x ,tempet[it], pet[it], rhoet[it], uet[it],]).T df.columns = cols df.to_csv(f"time{round(t,3)}.csv", index=False, sep='\t') t = t + dt it += 1 |
以下のようにcsvファイルが出力されます。
- time0.001.csv
- time0.001.csv
- time0.002.csv
- time0.003.csv
- time0.004.csv
- time0.005.csv
- time0.006.csv
- time0.007.csv
time0.007.csv
|
1 2 3 4 5 6 7 8 |
#x[m] temp[K] p[Pa] rho[kg/m3] u[m/s] -5.0 348.432 100000.0 0.9996462441060816 0.0 -4.9 348.432 100000.0 0.9996462441060816 0.0 -4.800000000000001 348.432 100000.0 0.9996462441060816 0.0 -4.700000000000001 348.432 100000.0 0.9996462441060816 0.0 -4.600000000000001 348.432 100000.0 0.9996462441060816 0.0 -4.500000000000002 348.432 100000.0 0.9996462441060816 0.0 -4.400000000000002 348.432 100000.0 0.9996462441060816 0.0 |
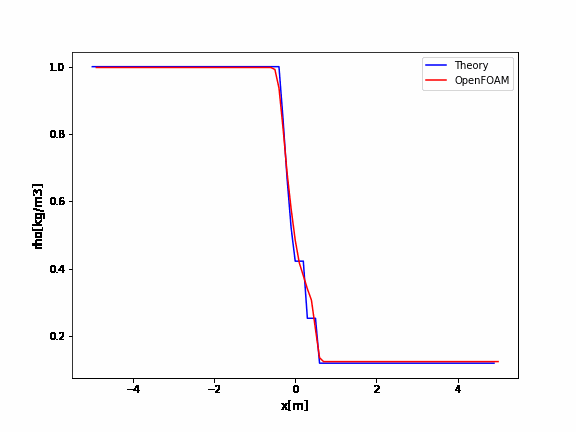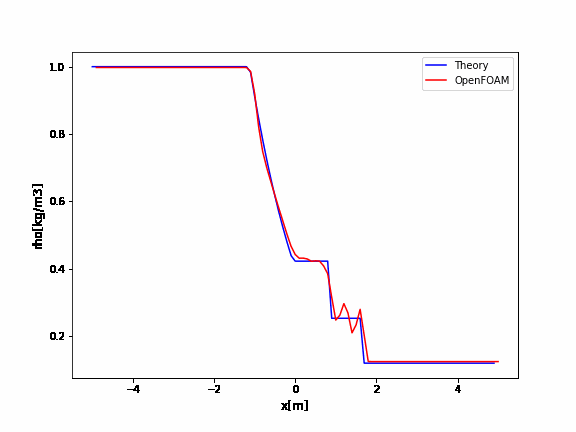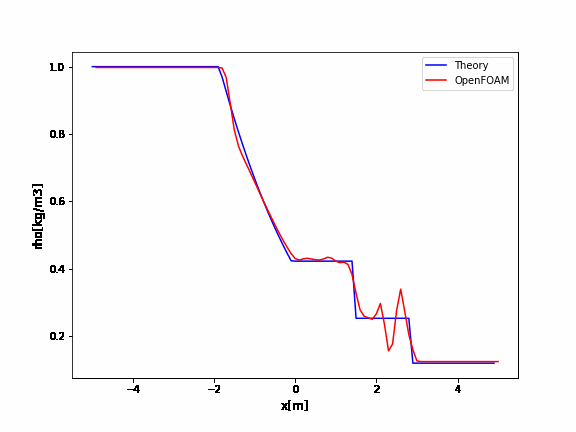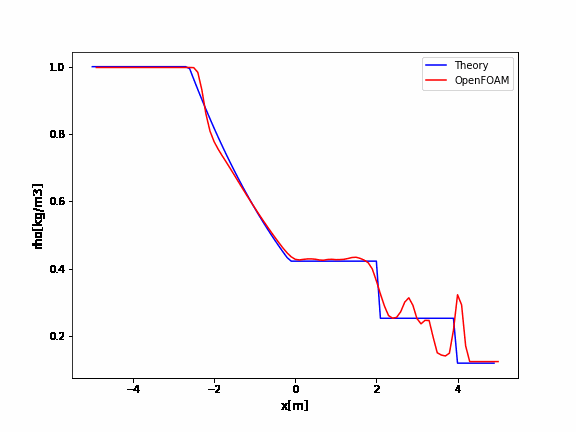
OpenFOAMの結果と比較
OpenFOAMの衝撃波菅はshock tubeというチュートリアルとして用意されています。
ソルバはsonicFoamとrhoCentralFoamがあり、どちらも超音速近辺での圧縮性のソルバです。
今回はrhoCentralFoamのshock tubeのチュートリアルの結果と上で示した理論解との比較を行います。
|
1 2 3 |
cp -r $FOAM_TUTORIALS/compressible/rhoCentralFoam/shockTube/ postProcess -func sampleDict -noFunctionObjects rhoCentralFoam |
モデルを少し編集しています。
必要とする流速はx方向のみであるためmag(U)を出力しておきます。
system/controlDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
application rhoCentralFoam; startFrom startTime; startTime 0; stopAt endTime; endTime 0.007; deltaT 1e-06; writeControl adjustable; writeInterval 0.001; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable true; adjustTimeStep yes; maxCo 0.5; maxDeltaT 1; functions { #includeFunc mag(U) } |
物理量の取得のためにsampleDictを用意します。
system/sampleDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
sampleDict { type sets; libs (sampling); setFormat raw; interpolationScheme cellPoint;//cell; fields (T mag(U) p rho); writeControl writeTime; sets ( x_sec { type face; axis x; start (-5 0 0); end (5 0 0); nPoints 200; } ); } |
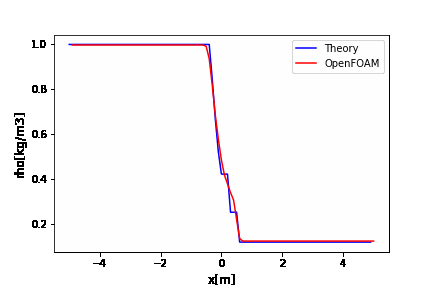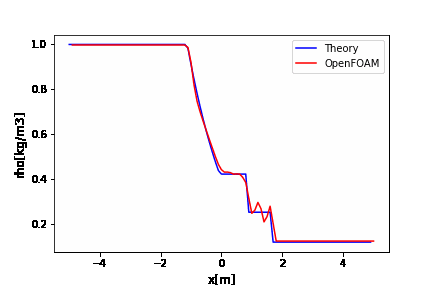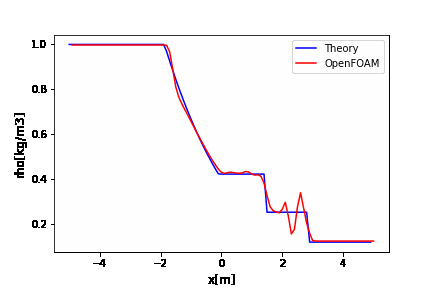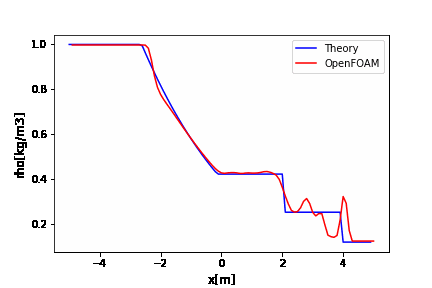
ここから適当にPythonで厳密解とOpwnFOAMを比較するためのアニメーションを作成します。密度を出力するプログラムのみを示しますが、流速と圧力も同様にアニメーション作成ができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation import pandas as pd fig = plt.figure(figsize=(8,6)) x = np.arange(XL, XR, dx) # OpenFOAMのデータフレーム作成関数 def df_cae_func(time_): datafilename = "x_sec_T_mag(U)_p_rho.xy" filenamepath = f"../shockTube/postProcessing/sampleDict/{time_}/{datafilename}" cols = ["x[m]", "T[K]", "U[m/s]", "p[Pa]", "rho[kg/m3]"] df_cae = pd.read_table(filenamepath, names=cols) return df_cae # アニメーション ims_rho_exp_cae = [] it = 0 t = 0 df_cae = pd.DataFrame() while t <= tstop: time = round(t,4) if time>0 and time%0.0010 == 0: if time == 0.0070: # 理論解 im_rho = plt.plot(x, rhoet[it], color="black",label="Theory") # OpenFOAM df_cae = df_cae_func(time) im_rho_cae = plt.plot(df_cae["x[m]"].values, df_cae["rho[kg/m3]"].values, color="red", label="OpenFOAM") else: # 理論解 im_rho = plt.plot(x, rhoet[it], color="black")#, label="Theory") # OpenFOAM df_cae = df_cae_func(time) im_rho_cae = plt.plot(df_cae["x[m]"].values, df_cae["rho[kg/m3]"].values, color="red")#, label="OpenFOAM") ims_rho_exp_cae.append(im_rho + im_rho_cae) t = t + dt it += 1 plt.xlabel("x[m]", fontsize=12) plt.ylabel("rho[kg/m3]", fontsize=12) plt.legend() ani_rho = animation.ArtistAnimation(fig, ims_rho_exp_cae, interval=1)#, repeat_delay=1000) ani_rho.save('rho_exp_cae.gif', writer='pillow') |
以下は自身のフォルダ構成に合わせて変更
- datafilename：OpenFOAMの結果ファイル名
- filenamepath ：相対パス
以下は密度を出力するプログラムです。
同様に流速と圧力も出力してみます。
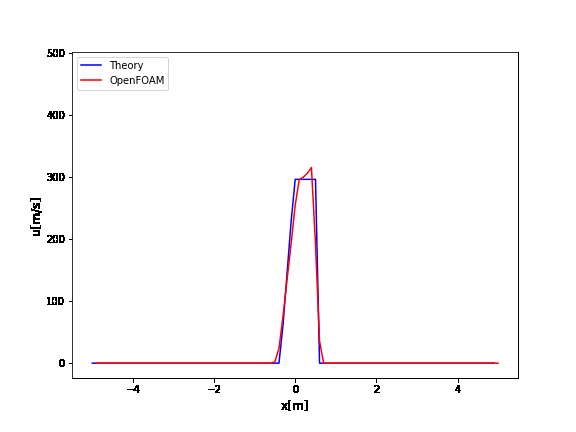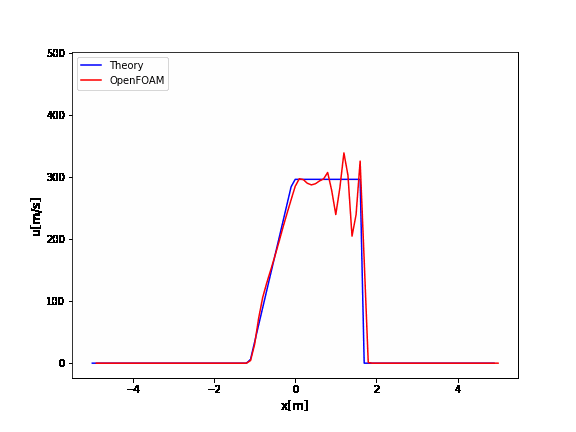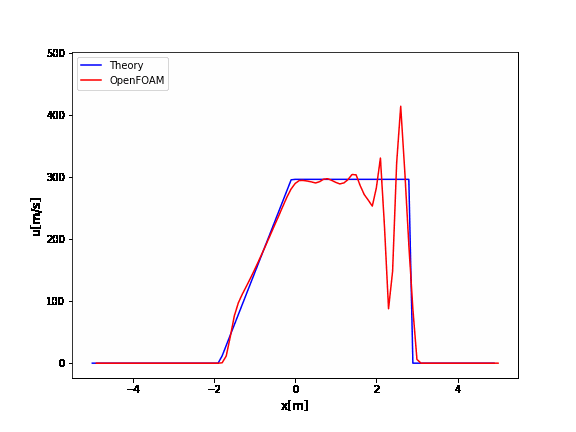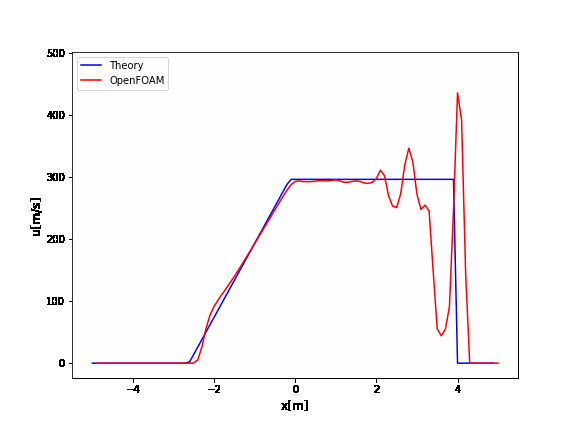
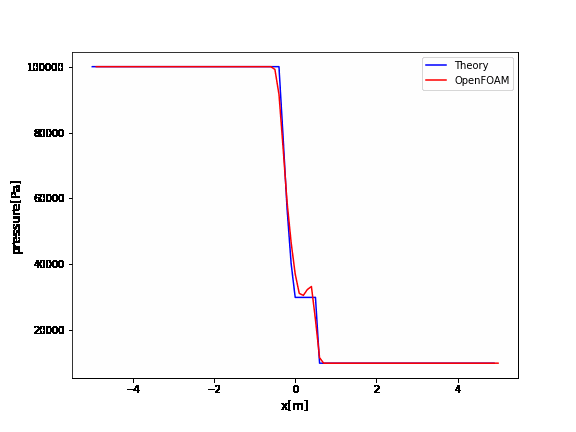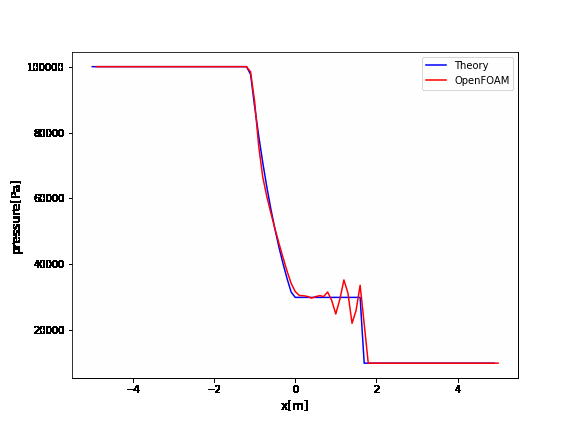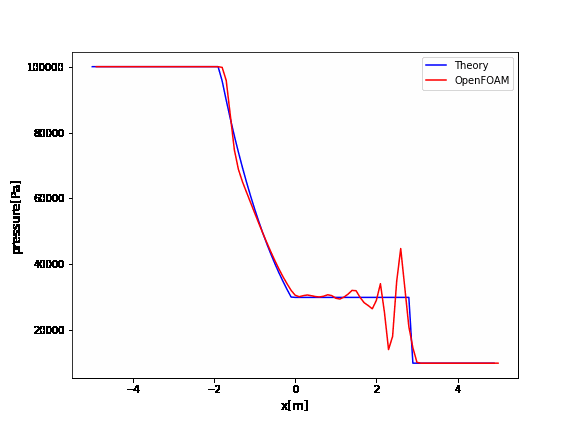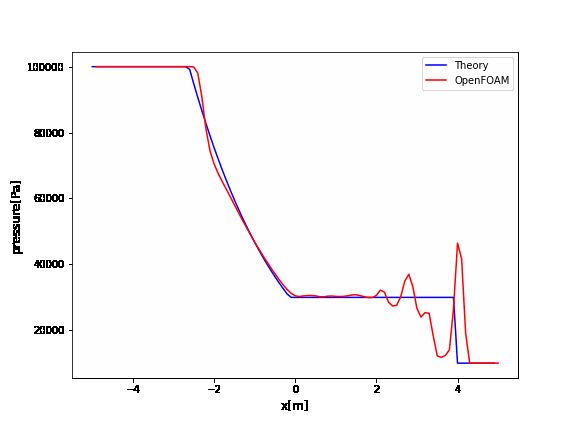
OpenFOAMのrhoCentralFoamのチュートリアルはデフォルトでかなり振動していますね。
厳密解と比較するとよくわかります。
この振動を抑えるためには、
- クーラン数を小さくする（時間刻みを小さくする）
- メッシュを細かくする
- 安定する離散化スキームを使う
などが挙げられます。
例えばクーラン数を0.09にすると以下のように改善されます。
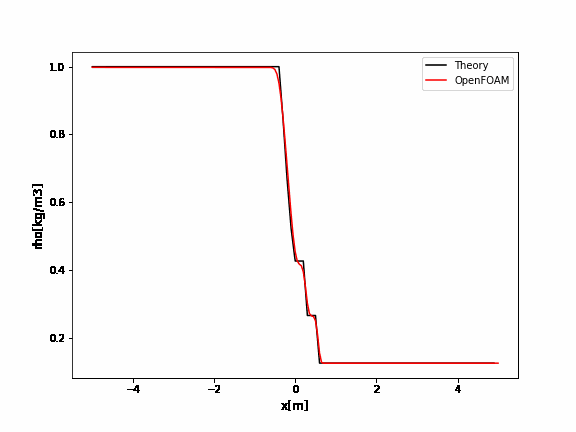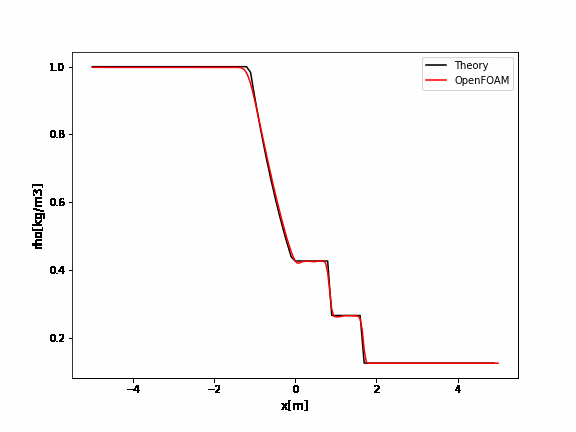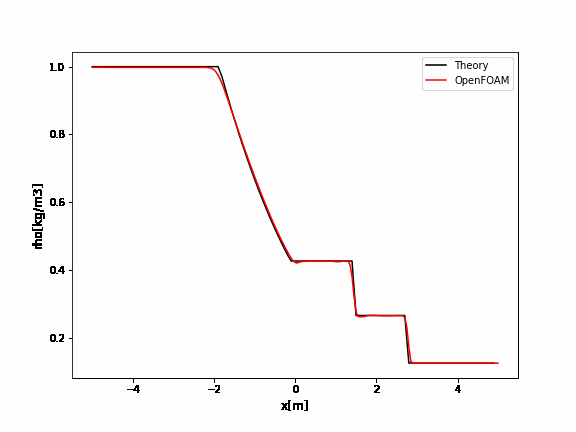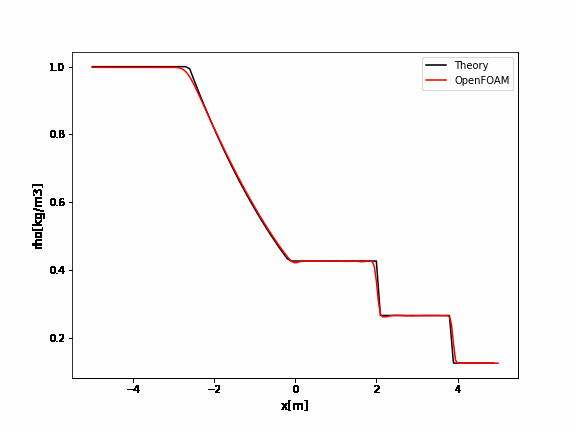
こちらに解析ケースとParaViewでのグラフ作成、gnuplotでのグラフ作成のデータをアップしました。
参考書
圧縮性流体についてはこちらの参考書がおすすめです。
本記事の理論解はこちらの参考書のプログラムを参考にしています。
C言語（タイトルにC++とあるが・・）で書かれたプログラムをPythonに書き換えたのが本記事で内容です。
数値流体解析の基礎 – Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 –
鋒, 肖, 孝夫, 長崎
3,960円(11/21 09:40時点)
Amazonの情報を掲載しています
☟こちらは、OpenFOAMの日本語書籍が無い中唯一わかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
Mari´c,Tomislav, H¨opken,Jens, Mooney,Kyle
8,250円(11/21 14:43時点)
Amazonの情報を掲載しています
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)
川畑 真一
2,376円(11/20 18:43時点)
発売日: 2022/04/15
Amazonの情報を掲載しています
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
Follow @t_kun_kamakiri
