【第4回Python流体の数値計算】１次元移流方程式を差分法で実装する。

こんにちは(@t_kun_kamakiri)。

今回は、「１次元の移流方程式」をPythonで実装するというのやります。

基本的な内容はこちらのサイトにそってやっていきます。

この記事ではこんな人を対象にしています。

こんな人が対象

Pythonを使い始めたけどどう使うかわからない
流体の数値計算をはじめて勉強する人

☟前回の記事がまだの人はこちらから

前回の記事

【第3回Python流体の数値計算】「参照渡し」と「値渡し」の違いを理解する。

今回からは、流体の基礎となる方程式に入っていくのですが、いきなりナビエストークス方程式を扱っても理解が追い付かないと思っています。

ナビエストークス方程式の各項には意味があり、各項をひとつひとつ見ていくことで理解が深まってくると考えています。

今回の内容

１次元移流方程式の差分法で離散化してPythonで解く！

☟移流方程式というのはナビエストークス方程式の左辺の二項のみを使った偏微分方程式です。

では、Google Colaboratoryを使ってコードを書きながら理解を深めていきたいと思います。

１次元移流方程式とは
移流方程式を離散化する
Pythonを使って移流方程式の数値計算
全体のコード
まとめ
Pythonの完全初心者は書籍で学ぶとよい

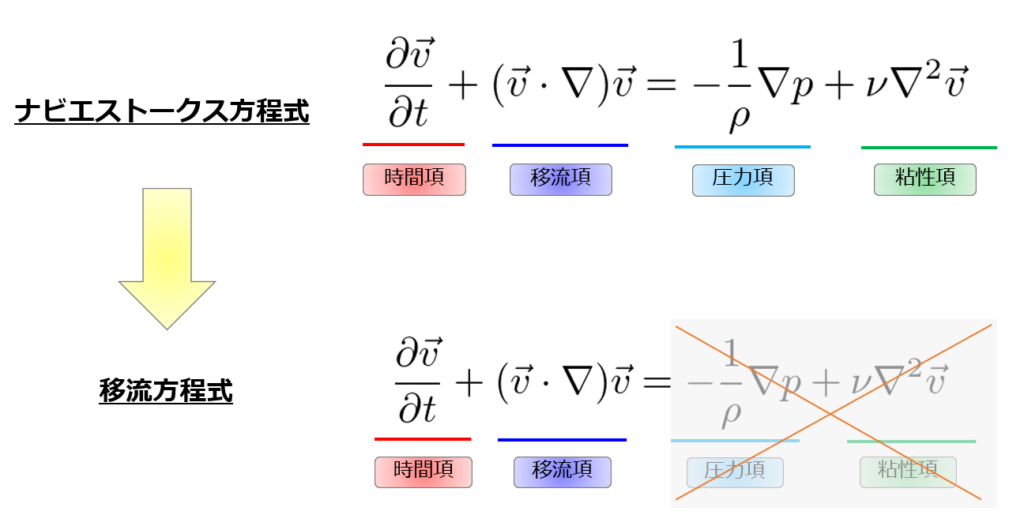
１次元移流方程式とは

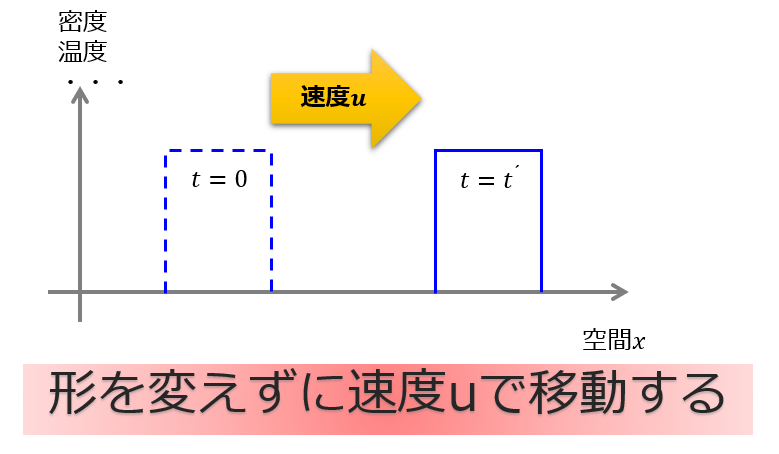
移流方程式について簡単な解説をしておこうと思います。

ナビエストークス方程式を取り扱う前に「移流方程式」について考えましょう。

\begin{align*}
\frac{\partial u}{\partial t}+c\frac{\partial u}{\partial x}=0\tag{1}
\end{align*}

速度\(c\)を持った波が\(+x\)方向に伝播する方程式です。

これは、微小時間\(\Delta t\)の間に速度が以下のように変化すると考えれば良い。

\begin{align*}
\Delta u =u(x+dx,t+dt)-u(x,t)\tag{2}
\end{align*}

に対して、\(\Delta u =0\)のとき「移流方程式」が導かれます。

\begin{align*}
\Delta u &=u(x+c\Delta t,t+\Delta t)-u(x,t)\\
&=u(x+c\Delta t,t+\Delta t)-u(t, x+c\Delta t)\\
&+u(x+c\Delta t,t)-u(x,t)\\
&=\frac{u(x+c\Delta t,t+\Delta t)-u(x+c\Delta t,t)}{\Delta t}\Delta t\\
&+\frac{u(x+c\Delta t,t)-u(x,t)}{\Delta x}\Delta x\\
&=\frac{\partial u}{\partial t}\Delta t+c\frac{\partial u}{\partial t}\Delta t
\end{align*}

\(\Delta t \rightarrow \infty,\Delta x \rightarrow \infty\)と考えれば最後の式で微分書き換えることができます。
ここから、移流方程式の(1)は、最後に両辺\(\Delta t\)で割り\(\frac{\Delta u}{\Delta t} =0\)となる方程式であることがわかります。

ナビエストークス方程式には一般解が見つかっていないのですが、移流方程式には一般解があります。

移流方程式の一般解

\begin{align*}
u(t,x)=u(x-ct)
\end{align*}

です。

この方程式の特徴は「初期状態のまま形を変えずに+x方向に伝播する解」です。

※もちろん\(u(t,x)=u(x+ct)\)のような「初期状態のまま形を変えずに-x方向に伝播する解」も存在します。

(1)式に代入してみれば、解となっているのが確認できますので代入してみてください。

カマキリ

では、移流方程式を離散化してみます。

移流方程式を離散化する

偏微分方程式をパソコンで解くには微分項を離散化して代数的に取り扱う必要があります。

(1)式の偏微分方程式には一般解があるので、わざわざ数値計算をするまでも無いのですが、今後取り扱う予定のナビエストークス方程式には一般解が見つかっておりません。

ですので、ナビエストークス方程式は数値計算で方程式の振る舞いを観測するしかありません。

数値計算の練習のために、ここで「移流方程式」の数値シミュレーションをやっておけば後々理解が深まるでしょう。

この偏微分方程式を離散化するにあたって、

時間微分の項（第一項）
空間微分の項（第二項）

をどのように扱うのかが問題です。

時間微分の項（第一項）

\begin{align*}
\frac{\partial u}{\partial t} \approx \frac{u(t+\Delta t)-u(t)}{\Delta t}\tag{3}
\end{align*}

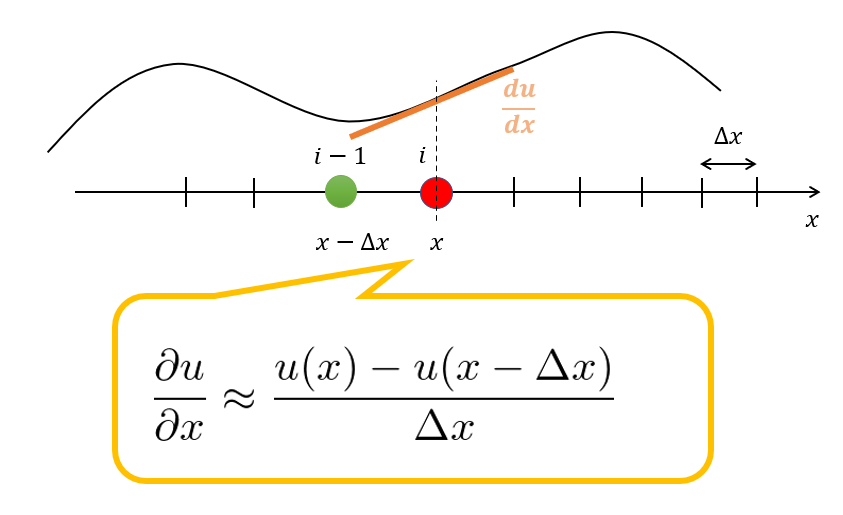
空間微分の項（第二項）

\begin{align*}
\frac{\partial u}{\partial x} \approx \frac{u(x)-u(x-\Delta x)}{\Delta x}\tag{4}
\end{align*}

空間微分にの項に関しては、ある時刻\(t\)において、ちょうど隣通しのセルにおける変化量を意味しています。

位置\(x\)に対してはセルの番号を\(i\)で下付き添え字にして、時間\(t\)に対しては計算のステップ数\(n\)として上付きの添え字にします。

そのようなルールに従うと(1)式の離散化は以下のようになります。

\begin{align*}
\frac{u^{n+1}_{i}-u^{n}_{i}}{\Delta t}+c\frac{u^{n}_{i}-u^{n}_{i-1}}{\Delta x}=0\tag{5}
\end{align*}

上記のように空間に対しては、自身の位置\(i\)番目よりも後ろの位置\(i-1\)を使って一階微分を表現しているので後退差分と呼ばれています。

今ほしい情報は、時刻tでのu(x)の振る舞いなので、n+1ステップ後の\(u^{n+1}_{i}\)について解きます。
※もちろんあるnステップでのある場所（i番目の格子点）ではなく、計算領域の全ての格子点での値を知りたいってことです。

(5)式を\(u^{n+1}\)について解くと、

\begin{align*}
u^{n+1}_{i}=u^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(u^{n}_{i}-u^{n}_{i-1}\big)\tag{6}
\end{align*}

Pythonを使って移流方程式の数値計算

それでは数値計算に移ります。

カマキリ

いきなり全部のコードを書くとわかりにくいので、ひとつひとつコードの解説を加えながら記述していきます。

Pythonのライブラリをインポート

まずは、ここで必要なPythonのライブラリをインポートします。

【必要なライブラリ】

Numpy：数値計算用のライブラリ
Matplotlib：波の形状を2次元プロットして可視化するためのライブラリ

Pythonのコードを書きます。

import numpy as np
import matplotlib.pyplot as plt

1 2	import numpy as np import matplotlib.pyplot as plt

実行してエラーがなければ記述に問題はないでしょう。
※Google Colaboratoryには標準で「NUmpy」と「Matplotlib」が搭載されているので特にエラーなく使えます。

初期条件を設定

次に「初期状態の設定」を行います。

数値計算をする際に特に単位は決まっていませんが、流体解析の場合はSI単位系(m-sec-kg)としておくのが良いかと思います。

【初期設定】

時間刻みは0.25[s]
速度c=1[m/s]

空間\(x\)は「0～2(m)」を41分割します。

Pythonのコードを書きます。

nx = 41
dx = 2 / (nx-1)
nt = 25 
dt = .025 
c = 1  

x = np.linspace(0,2,nx)

print('dx=',dx)
print('x=',x)
print(len(x))
print(type(x))

nx = 41

dx = 2 / (nx-1)

nt = 25

dt = .025

c = 1

x = np.linspace(0,2,nx)

print('dx=',dx)

print('x=',x)

print(len(x))

print(type(x))

【結果】

dx= 0.05
x= [0.   0.05 0.1  0.15 0.2  0.25 0.3  0.35 0.4  0.45 0.5  0.55 0.6  0.65
 0.7  0.75 0.8  0.85 0.9  0.95 1.   1.05 1.1  1.15 1.2  1.25 1.3  1.35
 1.4  1.45 1.5  1.55 1.6  1.65 1.7  1.75 1.8  1.85 1.9  1.95 2.  ]
41
<class 'numpy.ndarray'>

dx= 0.05

x= [0. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65

0.7 0.75 0.8 0.85 0.9 0.95 1. 1.05 1.1 1.15 1.2 1.25 1.3 1.35

1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9 1.95 2. ]

今回は確認のために「dxの値」「xの要素」「xの要素の数」「xの型」を出力しておきました。

np.ones(数)

次に、\(u\)の初期状態を決めておきまます。

【\(u\)の初期状態】

np.onesですべての要素の値を１にする
間だけ要素の値を２に変更する

☟つまり、このように初期状態を決めます。

Pythonのコードを書きます。

u = np.ones(nx)

print(u)
print(len(u))
print(type(u))

u = np.ones(nx)

print(u)

print(len(u))

print(type(u))

【結果】

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
41
<class 'numpy.ndarray'>

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.

1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

初期状態を「u」という変数で定義しています。

途中で結果を出力しながら自分が思っている設定になっているかを確認すると良いです。

これで要素の数がnx個で、値は全て１となりました。

次に、nx=41の要素のうち「10～21」の要素の値を「2」とします。

Pythonのコードを書きます。

u[int(.5 / dx):int(1 / dx + 1)] = 2

print(u)

u[int(.5 / dx):int(1 / dx + 1)] = 2

print(u)

【結果】

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

1 2	[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

これで\(u\)の初期状態ができました。

値だけを見ていてもわかりにくいので、Matplotlibで形状を確認してみましょう。

plt.plot(x,u)
plt.xlabel('x')
plt.ylabel('u')
plt.grid(alpha = 0.3)

plt.plot(x,u)

plt.xlabel('x')

plt.ylabel('u')

plt.grid(alpha = 0.3)

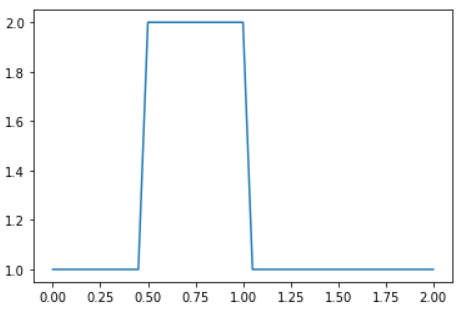
【結果】

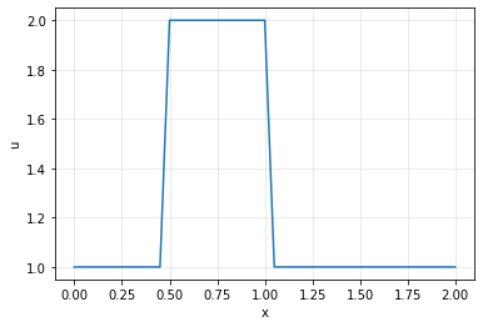
思っている形に初期状態ができています。
形を確認するだけならMatplotlibで「plt.plot(x,un)」だけで良いですが、ラベルとかグリッドを書いた方が見た目が良いのでお好みで設定できます。

移流方程式を解く

初期状態が設定できたのいよいよ移流方程式の数値計算を行います。
今回は時々刻々と変化する形状のアニメーション作成はせずに、最終的な形状だけをプロットしてみます。

【移流方程式を解く】

un = u.copy()で初期状態をコピーします。
u[i] = un[i] – c * dt / dx * (un[i] – un[i-1])とすることで(6)式、

\begin{align*}
u^{n+1}_{i}=u^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(u^{n}_{i}-u^{n}_{i-1}\big)\tag{6}
\end{align*}
を解いています。

では、Pythonのコードを書きます。

un = []
u = np.ones(nx)
u[int(.5 / dx):int(1 / dx + 1)] = 2


for n in range(nt): 
    un = u.copy()
    for i in range(1, nx):
        u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])

un = []

u = np.ones(nx)

u[int(.5 / dx):int(1 / dx + 1)] = 2

for n in range(nt):

un = u.copy()

for i in range(1, nx):

u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])

「for i in range(1,nx)」のように、空間の要素を0からではなく1からにしています。
これは、数値計算の途中で「un[i-1]」があるため「un[0]」を用意しておかないとエラーが起こってしまうため「un[0]」を初期状態で設定しておいたのです。
実際に計算で使っている空間領域は「要素の1～nx」だけということになります。

※Pythonの配列は基本が「値の参照渡し」なので、Google Colaboratoryのようにインタラクティブに計算を実行させていると値が思っていないところで上書きされていたりするので、今回は偏微分を解く部分に初期状態の設定を書いておくようにしました。

以上の数値計算を行っても何の結果も出ないと思いますので最終状態の「u」をMatplotlibで出力してみましょう。

plt.plot(x,u)

1	plt.plot(x,u)

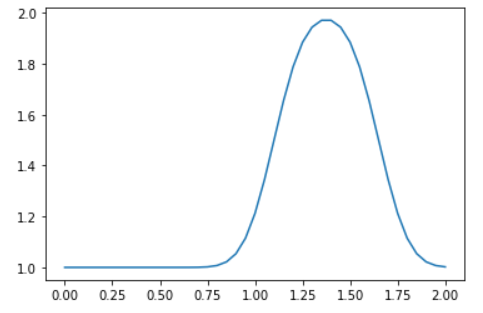
👆これが最終状態の「u」の形状です。

ちょっとわかりにくいので、初期状態と最終状態を比較してみます。

u_final = u.copy()

u_initial  = np.ones(nx)
u_initial[int(.5 / dx):int(1 / dx + 1)] = 2

plt.plot(x,u_initial,label = 'initial')
plt.plot(x,u_final, label = 'final')
plt.legend()

u_final = u.copy()

u_initial = np.ones(nx)

u_initial[int(.5 / dx):int(1 / dx + 1)] = 2

plt.plot(x,u_initial,label = 'initial')

plt.plot(x,u_final, label = 'final')

plt.legend()

※最終状態のuを「u_final = u.copy()」として違うアドレスを用意して参照するようにします。
※初期状態は新たに作り直しています。

【結果】

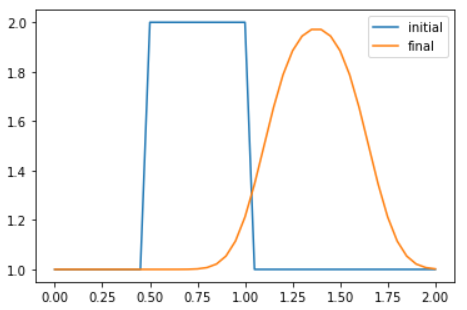
「初期状態のまま形を変えずに+x方向に伝播する解」であるのが移流方程式の厳密解なのに、思いっきり形が変わっていますね(‘ω’)

(1)式は一般解があるので、一般解に勝る最強の精度はないです。

厳密な解を得るためには数値計算の離散化を工夫しないといけないということですね・・・・

全体のコード

全体のコードを載せておきますので、コピペすることで移流方程式の数値計算ができます。

import numpy as np
import matplotlib.pyplot as plt

nx = 41
dx = 2 / (nx-1)
nt = 25 
dt = .025 
c = 1  

x = np.linspace(0,2,nx)

un = []
u = np.ones(nx)
u[int(.5 / dx):int(1 / dx + 1)] = 2


for n in range(nt): 
    un = u.copy()
    for i in range(1, nx):
        u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])

u_final = u.copy()

u_initial  = np.ones(nx)
u_initial[int(.5 / dx):int(1 / dx + 1)] = 2

plt.plot(x,u_initial,label = 'initial')
plt.plot(x,u_final, label = 'final')
plt.legend()

import numpy as np

import matplotlib.pyplot as plt

nx = 41

dx = 2 / (nx-1)

nt = 25

dt = .025

c = 1

x = np.linspace(0,2,nx)

un = []

u = np.ones(nx)

u[int(.5 / dx):int(1 / dx + 1)] = 2

for n in range(nt):

un = u.copy()

for i in range(1, nx):

u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])

u_final = u.copy()

u_initial = np.ones(nx)

u_initial[int(.5 / dx):int(1 / dx + 1)] = 2

plt.plot(x,u_initial,label = 'initial')

plt.plot(x,u_final, label = 'final')

plt.legend()

カマキリ

お試しあれ(^^)

まとめ

今回は「移流方程式」を離散化して空間に対して後退差分で数値計算を行いました。

結果は、初期状態から+x方向に伝搬するのですが形が変わって伝搬するという結果となりました。
数値計算の離散化をもう少し考えないといけないです・・・・が、今回は移流方程式を解いてみようという軽いノリなのでそこまでこだわりはしません。

本シリーズのナビエストークスの数値計算を終えた後に、離散化手法を見直していこうと思います。

☟ちなみに、こちらの記事に差分の仕方で「数値計算の安定性が全然違ってくる」というのを確認しています。

Pythonの完全初心者は書籍で学ぶとよい

Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）

確かな力が身につくPython「超」入門 (確かな力が身につく「超」入門シリーズ)

鎌田正浩

3,578円(11/24 20:59時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

僕自身もこの書籍ではじめは勉強しました。

小難しい余計なことが書いていないし、年末の一週間くらいで読むことができたので、初心者の方にはとてもお勧めです。

ちょっと応用編として以下の参考書がおすすめです。

Pythonによる数値計算とシミュレーション

小高知宏

2,750円(11/25 18:05時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

実際に偏微分を離散化して数値計算をするというのを経験することで実力が身につくと思います(^^)/

POSTED COMMENT

ikea より:

2023年6月30日 11:52

nx=41の要素のうち「10～21」の要素の値を「2」とするのを
u[int(.5 / dx):int(1 / dx + 1)] = 2で表現するのはなぜか教えていただきたいです。またfor n in range(nt): の部分はなぜnt=25を使っているかも教えていただきたいです

返信
- kamakiri より:
  
  2023年7月1日 23:54
  
  お読みいただきありがとうございます。
  dx = 2/40 = 0.05
  int(.5 / dx) = 0.5/0.05 = 10
  int(1 / dx + 1)] = 1/0.05 + 1 = 20 + 1 = 21
  ※intをつけているのは0.5/dxなどとした場合に浮動小数点となり整数値ではないのでエラーになるためです。
  　リストの要素の番号は整数である必要があるため。
  
  空間座標で言うと[0.5~1.05]までをu=2にしています。
  
  nt=25はここではタイムステップ数なので見たい現象が見れるタイムステップをご自身で決めれば良いです。
  ただし、dt = .025としているので、時間に直すとnt = 25は0.25*25で6.25秒です。
  6.25秒に特に意味はありません。
  見たい現象が見れるまでの最短の時間を設定しただけです。
  ntを小さすぎると見たい現象を見る前に計算が終わってしまいますし、ntが大きすぎると無駄に計算時間が増えてしまいます。
  
  よろしくお願いいたします。
  
  返信