こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
本記事ではOpenFOAMのメッシュ生成ユーティリティであるblockMeshを使って球体まわりのメッシュを6面体で生成したいと思います。
こちらの記事のモデル作成です。
参考記事
【OpenFOAM】ゴルフボールはどう打ったら最もよく飛ぶのか
※モデルを頂きブログ記事での解説のお許しを得たので皆さんに共有いたします。
記事内で「SALOMEを用いて下図のようなメッシュを作成しました。全てヘキサで作成した後にrefineMeshにて一部をポリヘドラに細分化」と書いてありますが、当ブログではゴルフボールではなくバスケットボールまわりのメッシュ作成をします。また、全てblockMeshのみで作成するので記事内の作り方と異なります。
最終的には以下のようになります。
前回の記事ではバスケットボールまわりの近傍のメッシュをblockMeshで作りました。
バスケットボールまわりの解析をするにあたって計算領域を広くとる必要があります。
今回はバスケットボールまわりの外部領域（計算領域）をblockMeshで作成します。
1度試しにsnappyHexMeshでメッシュ生成しましたが、バスケットボールの凹みの部分のメッシュを細かくしないといけなく計算時間がかかるので本記事の内容の通りメッシュを作成しなおすことにしました。
以前した球体でしたときの効力係数0.4より約4倍大きい。
メッシュがだめだな。 https://t.co/gcOkMWjD7j— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) September 2, 2022
バスケットボールはシュートの際に1秒間に2回転ほどしているそうです。
味方にパスをするときはもっと高速で回転していると思いますが、果たして回転させるとどう違うのか考察をしていく心意気です(^^)
カマキリ
自宅で解析できる記事は他にも書いています。
その他の記事
モデル作成と勉強しながら、アウトプットのため記事にまとめていきます。最終的にはOpenFOAMを使ってバスケットボールまわりの流れを解析します。
今後の予定
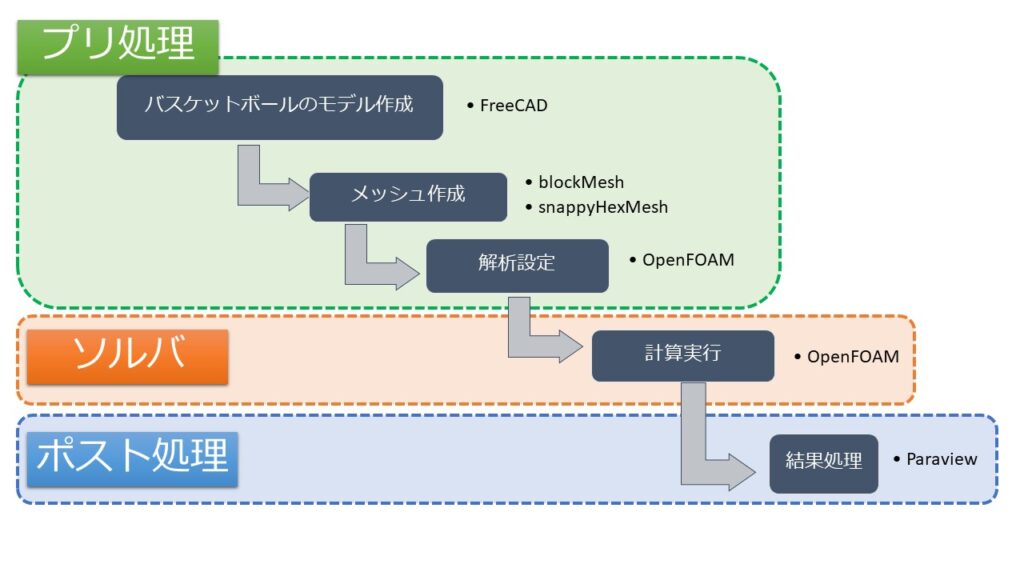
- 【回転するバスケットボールまわりの流れ(1)】FreeCADで作るバスケットボール
- 【回転するバスケットボールまわりの流れ(2)】ボール周辺をblockMeshでメッシュ作成
- 【回転するバスケットボールまわりの流れ(2)】外部領域ををblockMeshでメッシュ作成←本記
頑張りますよ(‘ω’)ノ
使用環境
- Windows11
- FreeCAD：0.20
- OpenFOAM-v2212 (2006)ESI版
- Paraview：5.11.0
ボール周辺のメッシュ作成
モデル作成の理解をするために段階的にメッシュを作成しましょう。
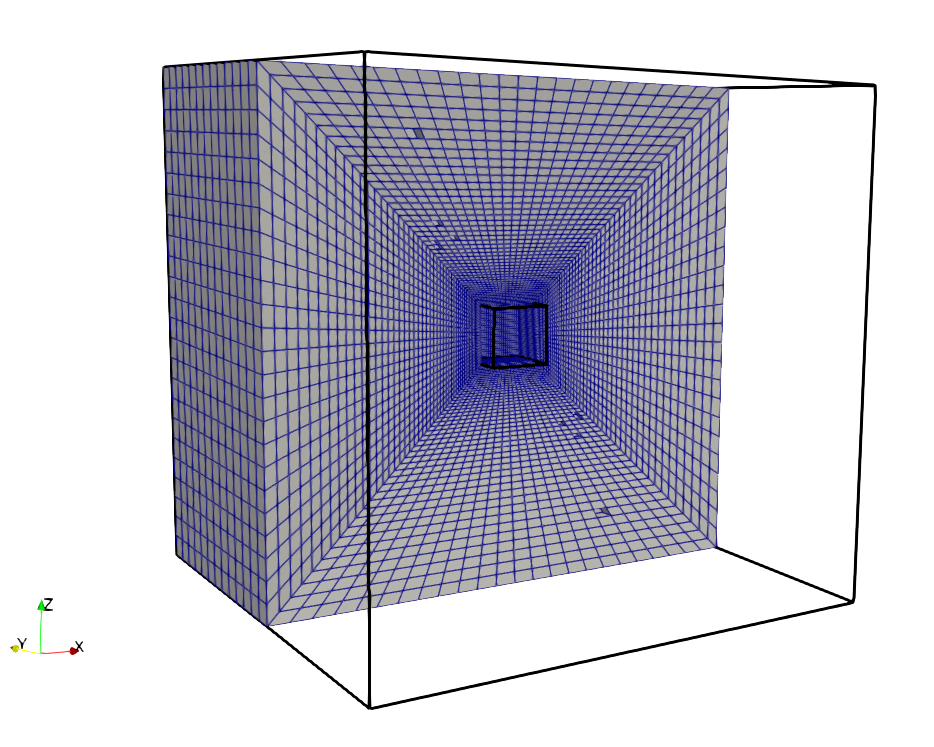
まずは以下のように大きな立方体の中に小さな立方体がくり抜かれた状態を作るためのblockMeshを作成します。
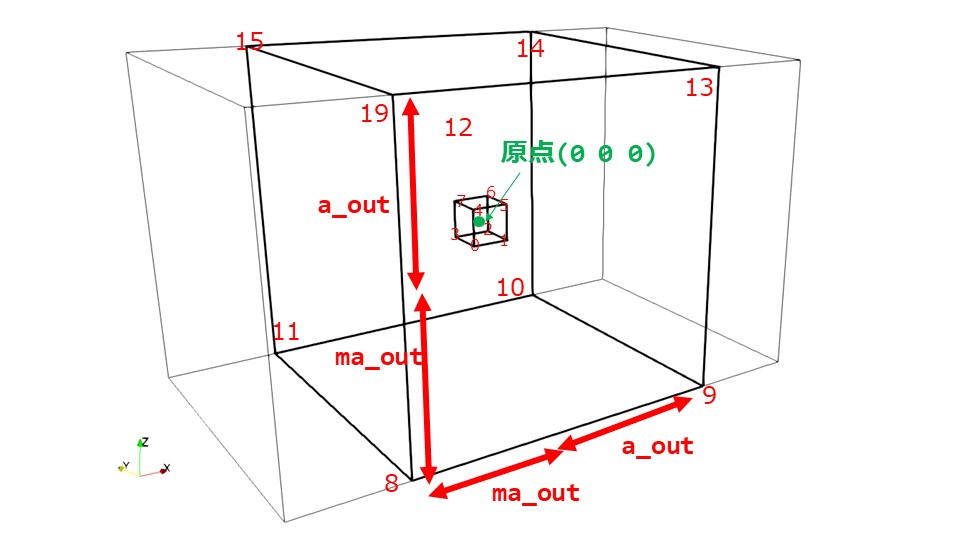
イメージしやすいように最終的な計算領域の大きさ薄い線を示しました。
ここで作成するのは太い黒線の領域です。
system/blockMeshDict_1
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
scale 1; verbose yes; // basketball r = 0.125m //r_in 0.128; r_ami 0.30; a_out 1.5; ma_out #calc "-$a_out"; x_in -2.5; x_out 2.5; geometry { } n 24; t 48; n_in 6; n_out 6; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; vertices ( ($mv_ami $mv_ami $mv_ami) // 0 ( $v_ami $mv_ami $mv_ami) // 1 ( $v_ami $v_ami $mv_ami) // 2 ($mv_ami $v_ami $mv_ami) // 3 ($mv_ami $mv_ami $v_ami) // 4 ( $v_ami $mv_ami $v_ami) // 5 ( $v_ami $v_ami $v_ami) // 6 ($mv_ami $v_ami $v_ami) // 7 ($ma_out $ma_out $ma_out) // 8 ( $a_out $ma_out $ma_out) // 9 ( $a_out $a_out $ma_out) // 10 ($ma_out $a_out $ma_out) // 11 ($ma_out $ma_out $a_out) // 12 ( $a_out $ma_out $a_out) // 13 ( $a_out $a_out $a_out) // 14 ($ma_out $a_out $a_out) // 15 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n $t) simpleGrading (1 1 0.1) hex (10 9 13 14 2 1 5 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 10 14 15 3 2 6 7) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 11 15 12 0 3 7 4) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 9 10 11 0 1 2 3) ($n $n $t) simpleGrading (1 1 0.1) hex (13 12 15 14 5 4 7 6) ($n $n $t) simpleGrading (1 1 0.1) ); edges ( ); faces ( ); boundary ( out_wall { type patch; faces ( ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (12 15 14 13) ); } out_to_in { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } ); |
blockMeshの実行はファイル指定でする場合は以下のようにします。
|
1 |
blockMesh -dict system/blockMeshDict_1 |
外部領域を広くとるためのメッシュを作成し
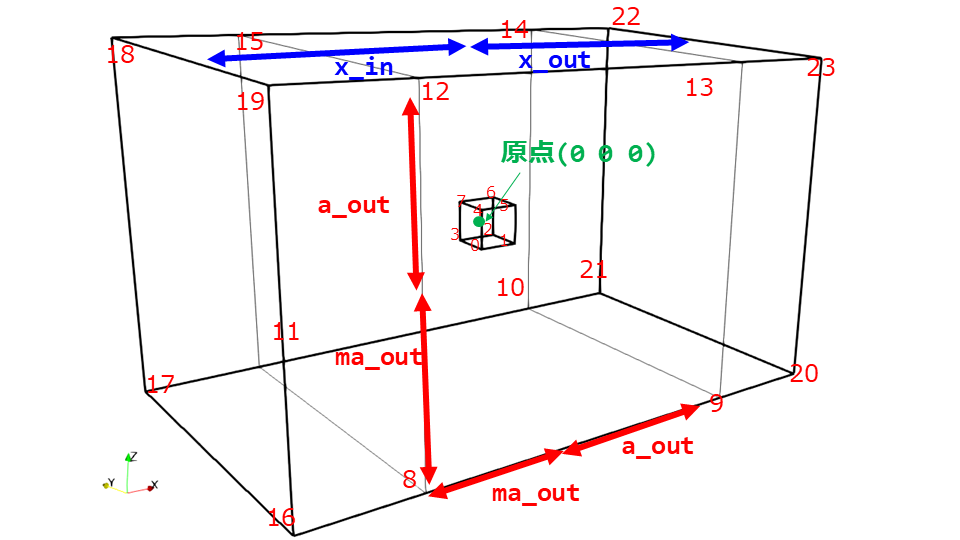
次に外部の計算領域を広くとるためのメッシュ作成をします。
以下のようなイメージになります。
system/blockMeshDict_2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
scale 1; verbose yes; // basketball r = 0.125m //r_in 0.128; r_ami 0.30; a_out 1.5; ma_out #calc "-$a_out"; x_in -2.5; x_out 2.5; geometry { } n 24; t 48; n_in 6; n_out 6; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; vertices ( ($mv_ami $mv_ami $mv_ami) // 0 ( $v_ami $mv_ami $mv_ami) // 1 ( $v_ami $v_ami $mv_ami) // 2 ($mv_ami $v_ami $mv_ami) // 3 ($mv_ami $mv_ami $v_ami) // 4 ( $v_ami $mv_ami $v_ami) // 5 ( $v_ami $v_ami $v_ami) // 6 ($mv_ami $v_ami $v_ami) // 7 ($ma_out $ma_out $ma_out) // 8 ( $a_out $ma_out $ma_out) // 9 ( $a_out $a_out $ma_out) // 10 ($ma_out $a_out $ma_out) // 11 ($ma_out $ma_out $a_out) // 12 ( $a_out $ma_out $a_out) // 13 ( $a_out $a_out $a_out) // 14 ($ma_out $a_out $a_out) // 15 ($x_in $ma_out $ma_out) // 16 ($x_in $a_out $ma_out) // 17 ($x_in $a_out $a_out) // 18 ($x_in $ma_out $a_out) // 19 ($x_out $ma_out $ma_out) // 20 ($x_out $a_out $ma_out) // 21 ($x_out $a_out $a_out) // 22 ($x_out $ma_out $a_out) // 23 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n $t) simpleGrading (1 1 0.1) hex (10 9 13 14 2 1 5 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 10 14 15 3 2 6 7) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 11 15 12 0 3 7 4) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 9 10 11 0 1 2 3) ($n $n $t) simpleGrading (1 1 0.1) hex (13 12 15 14 5 4 7 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 8 12 15 17 16 19 18) ($n $n $n_in) simpleGrading (1 1 1) hex (21 20 23 22 10 9 13 14) ($n $n $n_out) simpleGrading (1 1 1) ); edges ( ); faces ( ); boundary ( out_wall { type patch; faces ( ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (8 16 19 12) (12 19 18 15) (15 18 17 11) (11 17 16 8) (9 20 23 13) (13 23 22 14) (14 22 21 10) (10 21 20 9) (15 12 13 14) ); } out_to_in { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } inlet { type patch; faces ( (17 16 19 18) ); } outlet { type patch; faces ( (21 20 23 22) ); } ); |
blockMeshの実行はファイル指定でする場合は以下のようにします。
|
1 |
blockMesh -dict system/blockMeshDict_2 |
ここに前回作成したバスケットボール周辺のメッシュを重ねてみると以下のようになります。
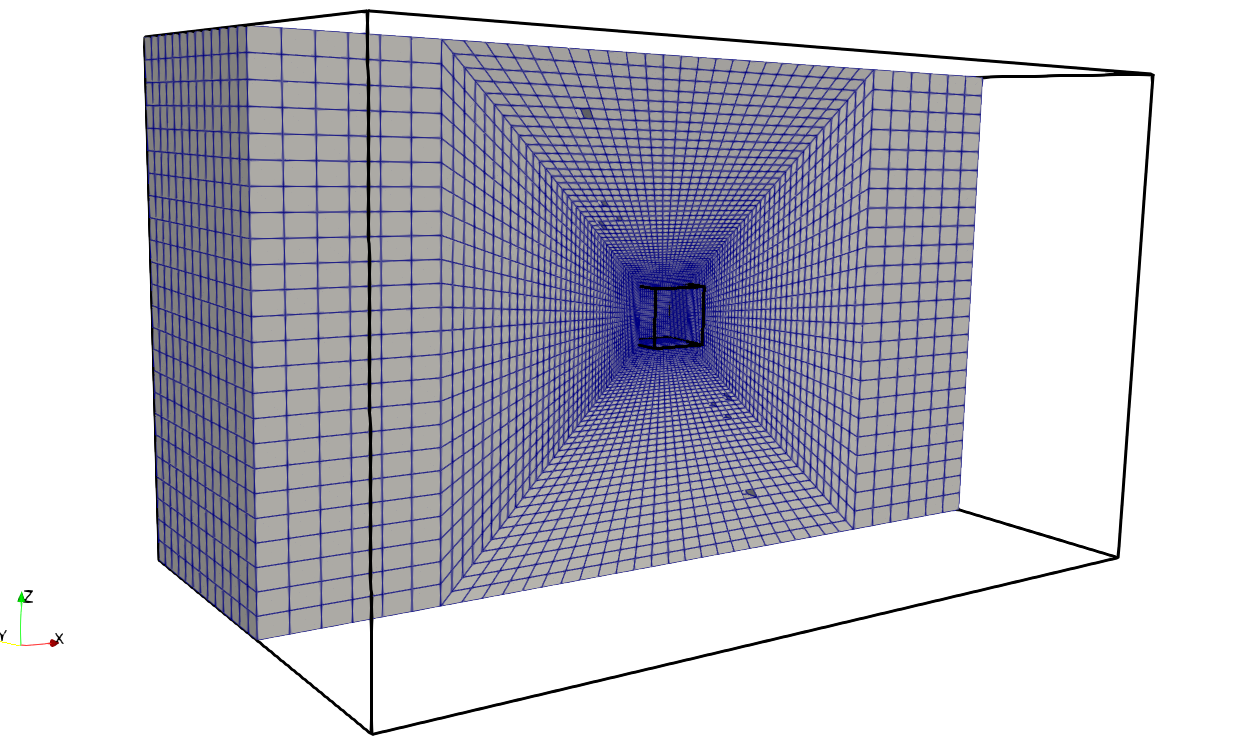
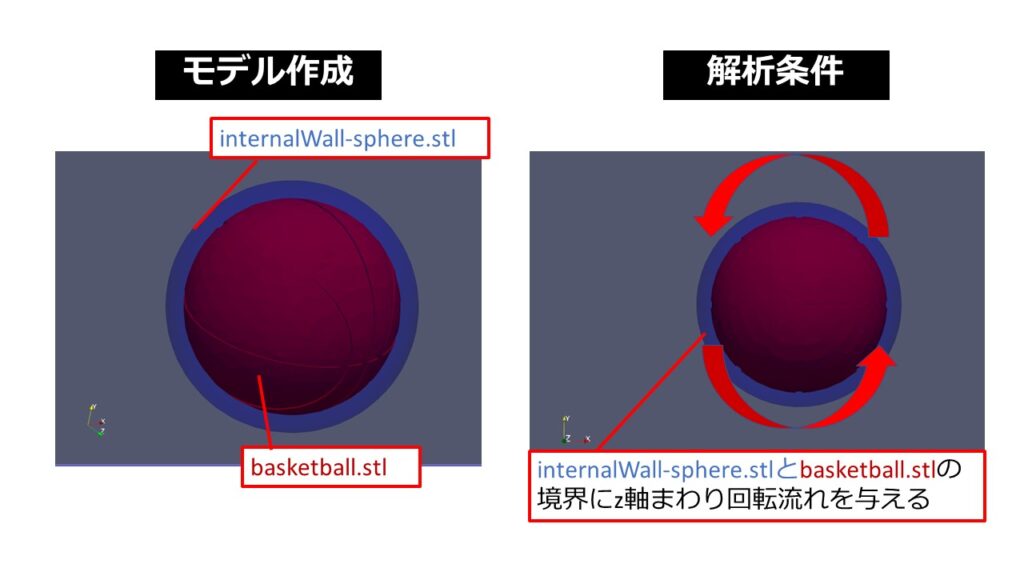
次に、今回作成した小さい立方体のまわりの形状を球体にしていきます。
小さな立方体を球体の形状に近づける
いきなり球体に近づけるのではなく少し球体に近づけるような操作をします。
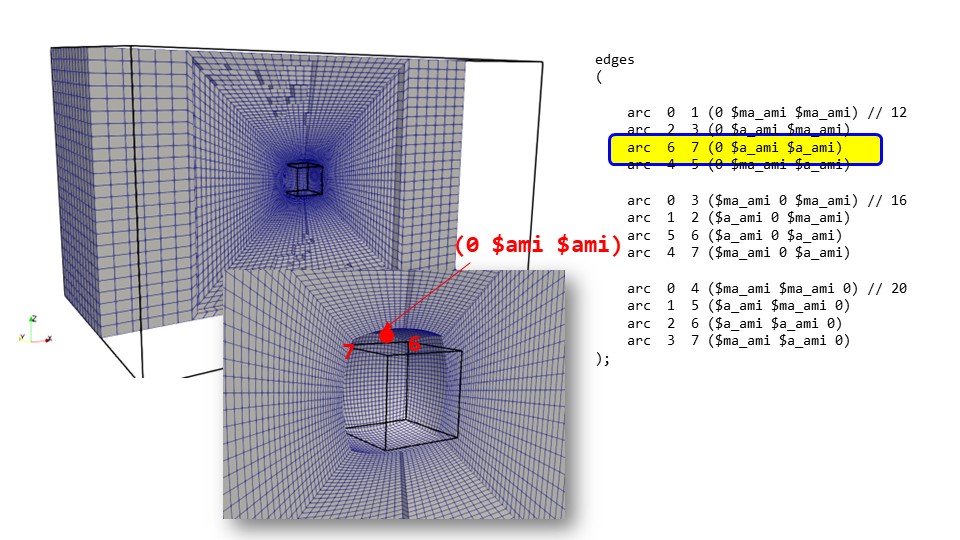
edgesで以下のような書き方をすると、始点(p1)から任意の点(x y z)を通って終点(p2)にいく曲線を描くようにメッシュを変形することができます。
|
1 |
arc p1 p2 (x y z) |
system/blockMeshDict_3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 |
scale 1; verbose yes; // basketball r = 0.125m //r_in 0.128; r_ami 0.30; a_out 1.5; ma_out #calc "-$a_out"; x_in -2.5; x_out 2.5; geometry { } n 24; t 48; n_in 6; n_out 6; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; vertices ( ($mv_ami $mv_ami $mv_ami) // 0 ( $v_ami $mv_ami $mv_ami) // 1 ( $v_ami $v_ami $mv_ami) // 2 ($mv_ami $v_ami $mv_ami) // 3 ($mv_ami $mv_ami $v_ami) // 4 ( $v_ami $mv_ami $v_ami) // 5 ( $v_ami $v_ami $v_ami) // 6 ($mv_ami $v_ami $v_ami) // 7 ($ma_out $ma_out $ma_out) // 8 ( $a_out $ma_out $ma_out) // 9 ( $a_out $a_out $ma_out) // 10 ($ma_out $a_out $ma_out) // 11 ($ma_out $ma_out $a_out) // 12 ( $a_out $ma_out $a_out) // 13 ( $a_out $a_out $a_out) // 14 ($ma_out $a_out $a_out) // 15 ($x_in $ma_out $ma_out) // 16 ($x_in $a_out $ma_out) // 17 ($x_in $a_out $a_out) // 18 ($x_in $ma_out $a_out) // 19 ($x_out $ma_out $ma_out) // 20 ($x_out $a_out $ma_out) // 21 ($x_out $a_out $a_out) // 22 ($x_out $ma_out $a_out) // 23 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n $t) simpleGrading (1 1 0.1) hex (10 9 13 14 2 1 5 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 10 14 15 3 2 6 7) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 11 15 12 0 3 7 4) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 9 10 11 0 1 2 3) ($n $n $t) simpleGrading (1 1 0.1) hex (13 12 15 14 5 4 7 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 8 12 15 17 16 19 18) ($n $n $n_in) simpleGrading (1 1 1) hex (21 20 23 22 10 9 13 14) ($n $n $n_out) simpleGrading (1 1 1) ); edges ( arc 0 1 (0 $ma_ami $ma_ami) // 12 arc 2 3 (0 $a_ami $ma_ami) arc 6 7 (0 $a_ami $a_ami) arc 4 5 (0 $ma_ami $a_ami) arc 0 3 ($ma_ami 0 $ma_ami) // 16 arc 1 2 ($a_ami 0 $ma_ami) arc 5 6 ($a_ami 0 $a_ami) arc 4 7 ($ma_ami 0 $a_ami) arc 0 4 ($ma_ami $ma_ami 0) // 20 arc 1 5 ($a_ami $ma_ami 0) arc 2 6 ($a_ami $a_ami 0) arc 3 7 ($ma_ami $a_ami 0) ); faces ( ); boundary ( out_wall { type patch; faces ( ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (8 16 19 12) (12 19 18 15) (15 18 17 11) (11 17 16 8) (9 20 23 13) (13 23 22 14) (14 22 21 10) (10 21 20 9) (15 12 13 14) ); } out_to_in { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } inlet { type patch; faces ( (17 16 19 18) ); } outlet { type patch; faces ( (21 20 23 22) ); } ); |
blockMeshの実行はファイル指定でする場合は以下のようにします。
|
1 |
blockMesh -dict system/blockMeshDict_3 |
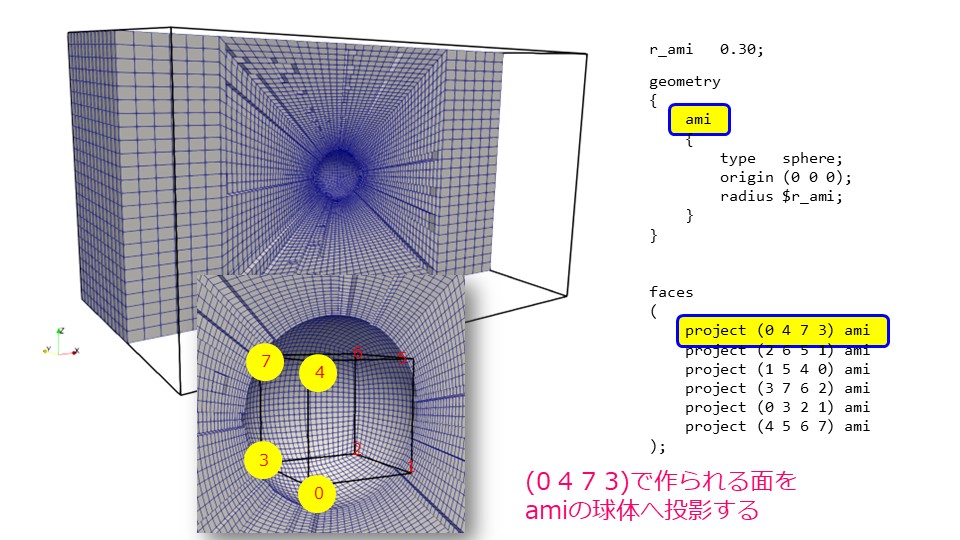
次に球体に投影するようにメッシュを変形させます。
球体になるようにメッシュを変形
system/blockMeshDict_4
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
scale 1; verbose yes; // basketball r = 0.125m //r_in 0.128; r_ami 0.30; a_out 1.5; ma_out #calc "-$a_out"; x_in -2.5; x_out 2.5; geometry { ami { type sphere; origin (0 0 0); radius $r_ami; } } n 24; t 48; n_in 6; n_out 6; v #calc "1.0/sqrt(3.0)"; a #calc "1.0/sqrt(2.0)"; v_ami #calc "$r_ami*$v"; mv_ami #calc "-$v_ami"; a_ami #calc "$r_ami*$a"; ma_ami #calc "-$a_ami"; vertices ( ($mv_ami $mv_ami $mv_ami) // 0 ( $v_ami $mv_ami $mv_ami) // 1 ( $v_ami $v_ami $mv_ami) // 2 ($mv_ami $v_ami $mv_ami) // 3 ($mv_ami $mv_ami $v_ami) // 4 ( $v_ami $mv_ami $v_ami) // 5 ( $v_ami $v_ami $v_ami) // 6 ($mv_ami $v_ami $v_ami) // 7 ($ma_out $ma_out $ma_out) // 8 ( $a_out $ma_out $ma_out) // 9 ( $a_out $a_out $ma_out) // 10 ($ma_out $a_out $ma_out) // 11 ($ma_out $ma_out $a_out) // 12 ( $a_out $ma_out $a_out) // 13 ( $a_out $a_out $a_out) // 14 ($ma_out $a_out $a_out) // 15 ($x_in $ma_out $ma_out) // 16 ($x_in $a_out $ma_out) // 17 ($x_in $a_out $a_out) // 18 ($x_in $ma_out $a_out) // 19 ($x_out $ma_out $ma_out) // 20 ($x_out $a_out $ma_out) // 21 ($x_out $a_out $a_out) // 22 ($x_out $ma_out $a_out) // 23 ); blocks ( hex ( 9 8 12 13 1 0 4 5) ($n $n $t) simpleGrading (1 1 0.1) hex (10 9 13 14 2 1 5 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 10 14 15 3 2 6 7) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 11 15 12 0 3 7 4) ($n $n $t) simpleGrading (1 1 0.1) hex ( 8 9 10 11 0 1 2 3) ($n $n $t) simpleGrading (1 1 0.1) hex (13 12 15 14 5 4 7 6) ($n $n $t) simpleGrading (1 1 0.1) hex (11 8 12 15 17 16 19 18) ($n $n $n_in) simpleGrading (1 1 1) hex (21 20 23 22 10 9 13 14) ($n $n $n_out) simpleGrading (1 1 1) ); edges ( arc 0 1 (0 $ma_ami $ma_ami) // 12 arc 2 3 (0 $a_ami $ma_ami) arc 6 7 (0 $a_ami $a_ami) arc 4 5 (0 $ma_ami $a_ami) arc 0 3 ($ma_ami 0 $ma_ami) // 16 arc 1 2 ($a_ami 0 $ma_ami) arc 5 6 ($a_ami 0 $a_ami) arc 4 7 ($ma_ami 0 $a_ami) arc 0 4 ($ma_ami $ma_ami 0) // 20 arc 1 5 ($a_ami $ma_ami 0) arc 2 6 ($a_ami $a_ami 0) arc 3 7 ($ma_ami $a_ami 0) ); faces ( project (0 4 7 3) ami project (2 6 5 1) ami project (1 5 4 0) ami project (3 7 6 2) ami project (0 3 2 1) ami project (4 5 6 7) ami ); boundary ( out_wall { type patch; faces ( ( 9 13 12 8) (11 15 14 10) ( 8 11 10 9) (8 16 19 12) (12 19 18 15) (15 18 17 11) (11 17 16 8) (9 20 23 13) (13 23 22 14) (14 22 21 10) (10 21 20 9) (15 12 13 14) ); } out_to_in { type wall; faces ( (0 4 7 3) (2 6 5 1) (1 5 4 0) (3 7 6 2) (0 3 2 1) (4 5 6 7) ); } inlet { type patch; faces ( (17 16 19 18) ); } outlet { type patch; faces ( (21 20 23 22) ); } ); |
blockMeshの実行はファイル指定でする場合は以下のようにします。
|
1 |
blockMesh -dict system/blockMeshDict_4 |
球体周りの計算領域ができました。
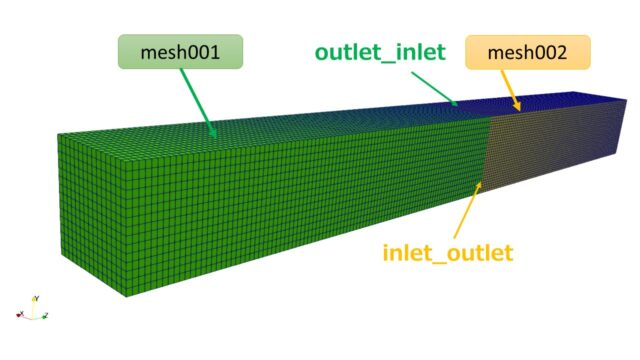
ここに前回作成したバスケットボール周辺のメッシュを重ねると以下のようになります。
- バスケットボール周辺：inner
- 外部の計算領域：outer
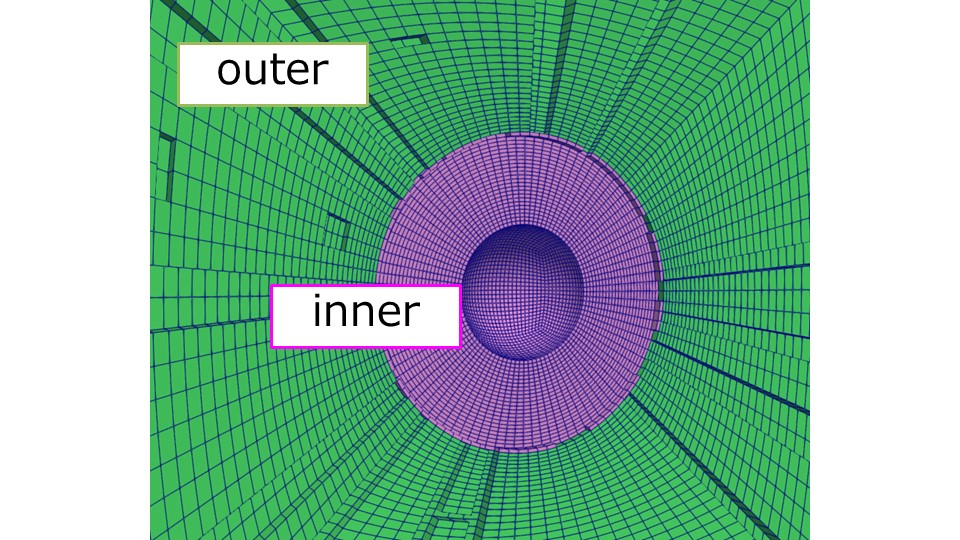
inner（前回記事で作成）とonter（今回作成）は境界で節点はつながっていません。
もしボールのまわりの解析をしたい場合は、以下の方法があります。
- 境界の節点をつないで解析をする(mergeMesh+stitchMesh)
- 境界面をcyclicAMIで周期境界にする(mergeMesh+cyclicAMI境界）
本記事でもこの2つの方法については解説を行う予定です。
参考記事
まとめ
今回はバスケットボールのまわりの計算領域をメッシュ作成をblockMeshのみ使ってメッシュ作成をしました。6面体で作成しているためメッシュ数を多くすることなく球体形状に沿ったメッシュ作成ができています。
次回はinner（前回記事で作成）とonter（今回作成）は境界をcyclicAMI境界条件にして球体周りの解析を行います。
解散した結果が以前球体周りの抗力係数をOpenFOAMで再現したような結果になるのかどうかを検証します。
この記事のメッシュ作成はblockMeshとsnappyHexMeshを使って作成していましたが、今回のようなblockMeshの6面体のみで作成した場合と結果に違いが出るのかを検証します。
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍として重宝しているわかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
OpenFOAMコードの辞書的な扱いとしては以下の参考書が大変役に立ちます。
本記事ではESI版のOpenFOAMを使っているため本書のFoundation版で対応していない部分がありますが、その辺を考慮しても持っていて損はないでしょう。
今回の記事はこちらの著者の方からモデル提供をいただきモデル作成の解説を行いました。
OpenFOAMでメッシュ作成
Follow @t_kun_kamakiri
