製品開発をしていると熱に関する問題に出くわすことが多いですよね。
当ブログでは伝熱工学の基礎的内容を以下のシリーズに分けて解説を行います。
今回は多層における熱伝導率の合成について図を用いながらわかりやすく解説をします。
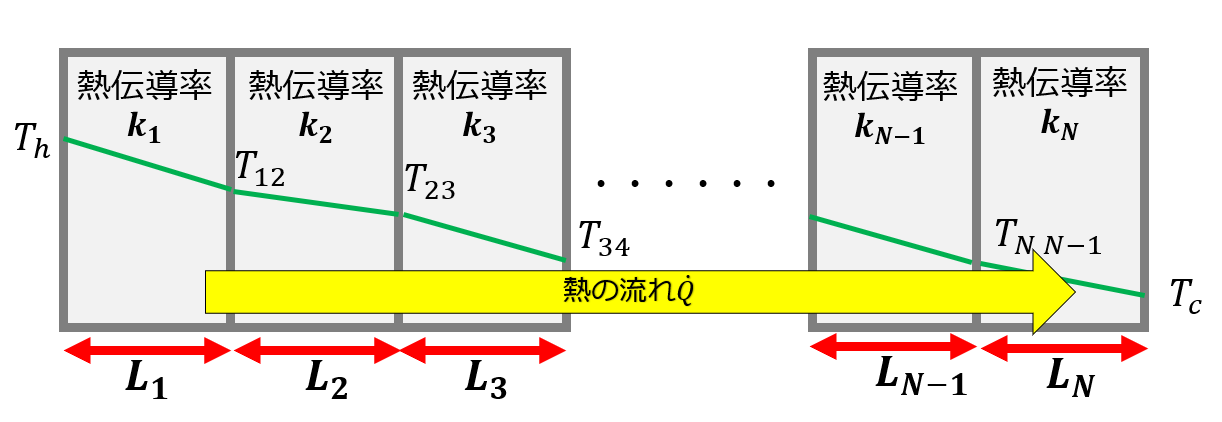
例えば以下のような平板が3層の場合の熱伝導を考えるにはどうするでしょうか？
3層の合成の熱伝導率を考えることができれば、両端の温度差からフーリエの法則を使って熱量が計算できますよね。
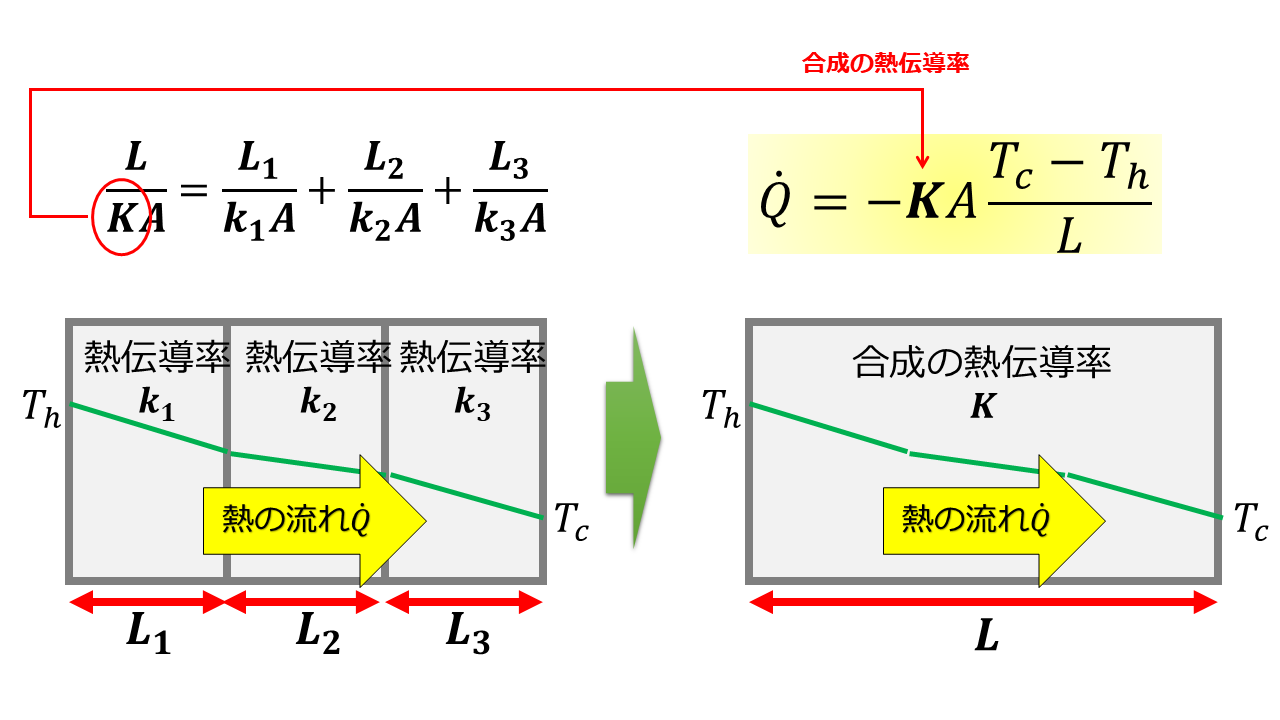
結論を先に言うと、合成の熱伝導率は$\frac{L}{KA}=\frac{L_{1}}{k_{1}A}+\frac{L_{2}}{k_{2}A}+\frac{L_{3}}{k_{3}A}$のように書けます。
こちらの導出方法を丁寧に解説します。
- 工学系の学生
- 製造業に勤める技術者
- 技術士を目指している技術者
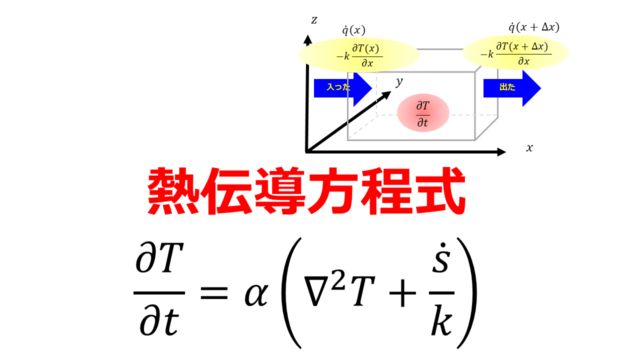
復習：フーリエの法則
熱伝導に関係する式には、単位面積・単位時間当たりの熱移動と単位長さあたりの温度差を熱伝導率という比例係数で結んだフーリエの法則があります。
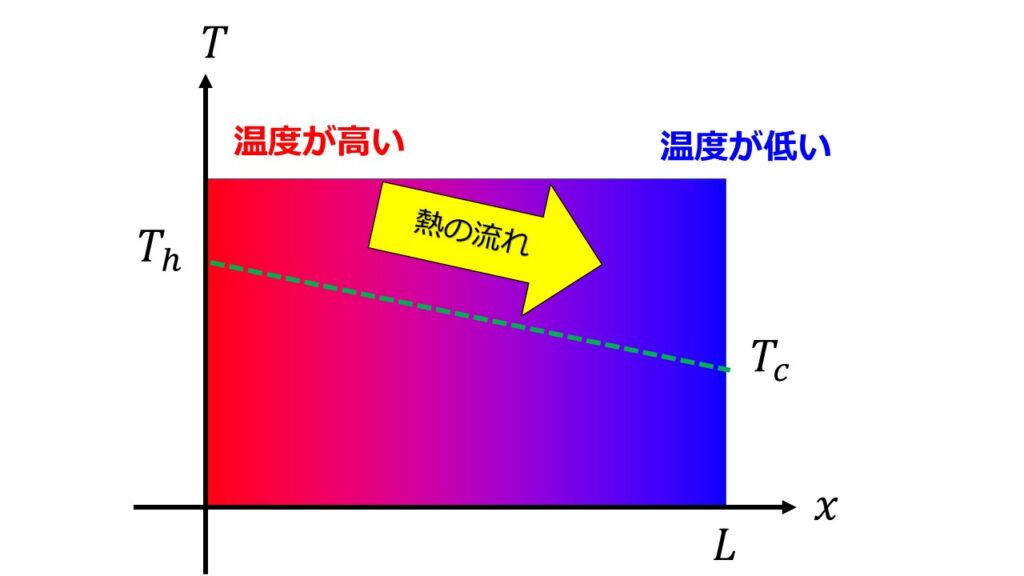
熱の移動は高い方から低い方へ移動するというものを熱伝導率$k$を使って記述します。
これにより単位時間当たりの熱の移動$\dot{Q}$[W]は、端点の温度差$T_{c}-T_{h}$と結びつけることができます。
\dot{Q}&=-kA\frac{T_{c}-T_{h}}{L}\\
&or\\
\dot{q}&=-k\frac{T_{c}-T_{h}}{L}\tag{1}
\end{align*}
- 熱伝導率：$k[W/m K]$
- 断面積：$A[m^2]$
、熱量$\dot{Q}$か、断面積$A$で割って熱流束$\dot{q}=\frac{\dot{Q}}{A}$で表しているかの違いです。
詳しくは前回の記事をご参考ください。
多層の場合の合成熱伝導率
では、続いて多層の場合の熱伝導率を考えましょう。
今回は3層ある場合で考えます。
右端の温度を$T_{h}$、左端の温度を$T_{c}$、左から1層目と2層目の間の温度を$T_{12}$、2層目と3層目の間の温度を$T_{23}$とします。
熱伝導率は左から$k_{1}$、$k_{2}$、$k_{3}$とします。
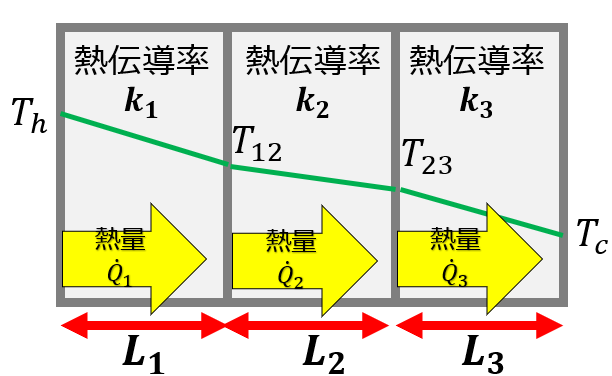
合成の熱伝導率を求める手順は以下です。
- 各層でフーリエの法則を使う
- 各層を通過する熱量は同じ
- 各層を1つであるとみなしたフーリエの法則を使う
具体的に計算してみましょう。
各層でフーリエの法則を使う
まずは各層の温度差から熱量を求めるフーリエの法則を立てます。
\dot{Q}_{1}&=-k_{1}A\frac{T_{12}-T_{h}}{L_{1}}\tag{2}\\
\dot{Q}_{2}&=-k_{2}A\frac{T_{23}-T_{12}}{L_{2}}\tag{3}\\
\dot{Q}_{3}&=-k_{3}A\frac{T_{c}-T_{23}}{L_{3}}\tag{4}
\end{align*}
式が立ったら以下のようにしておきます。
\dot{Q}_{1}\frac{L_{1}}{k_{1}A}&=-\big(T_{12}-T_{h}\big)\tag{2}\\
\dot{Q}_{2}\frac{L_{2}}{k_{2}A}&=-\big(T_{23}-T_{12}\big)\tag{3}\\
\dot{Q}_{3}\frac{L_{3}}{k_{3}A}&=-\big(T_{c}-T_{23}\big)\tag{4}
\end{align*}
各層を通過する熱量は同じ
(5)(6)(7)を足して各層の間の温度$T_{12},T_{23}$を消去します。
\dot{Q}_{1}\frac{L_{1}}{k_{1}A}+\dot{Q}_{2}\frac{L_{2}}{k_{2}A}+\dot{Q}_{3}\frac{L_{3}}{k_{3}A}=-\big(T_{c}-T_{h}\big)\tag{8}
\end{align*}
次に各層を通過する熱量は同じ$\dot{Q}_{1}=\dot{Q}_{2}=\dot{Q}_{3}=\dot{Q}$とします。
これは各層で熱量が保存していることを意味します。
熱量が保存しない場合は、どこかに熱源があったり熱の損失があったりするのですが、今回はそのようなことは考慮していません。
\dot{Q}\bigg(\frac{L_{1}}{k_{1}A}+\frac{L_{2}}{k_{2}A}+\frac{L_{3}}{k_{3}A}\bigg)=-\big(T_{c}-T_{h}\big)\tag{9}
\end{align*}
各層を1つであるとみなしたフーリエの法則を使う
(9)を見ると、各層に分かれていた熱の移動が各層の間の温度変化はどうであれ、以下のように端点の温度差$T_{c}-T_{h}$から熱移動を考えているという式になっています。
合成した右の絵でフーリエの法則を使うと、
\dot{Q}=-KA\frac{T_{c}-T_{h}}{L}\tag{10}
\end{align*}
となります。
(9)を(10)の形にすると、
\dot{Q}=-\frac{T_{c}-T_{h}}{\frac{L_{1}}{k_{1}A}+\frac{L_{2}}{k_{2}A}+\frac{L_{3}}{k_{3}A}}\tag{11}
\end{align*}
となります。
直列回路との類似
合成の熱伝導率は$K=\frac{L}{\frac{L_{1}}{k_{1}}+\frac{L_{2}}{k_{2}}+\frac{L_{3}}{k_{3}}}$とわかったけど、これは非常に覚えにくいですよね。
もう少し覚えやすい形で合成熱伝導率を理解したいと思います。
以下のように中学生で習ったような直列回路をイメージすると非常に覚えやすいです。
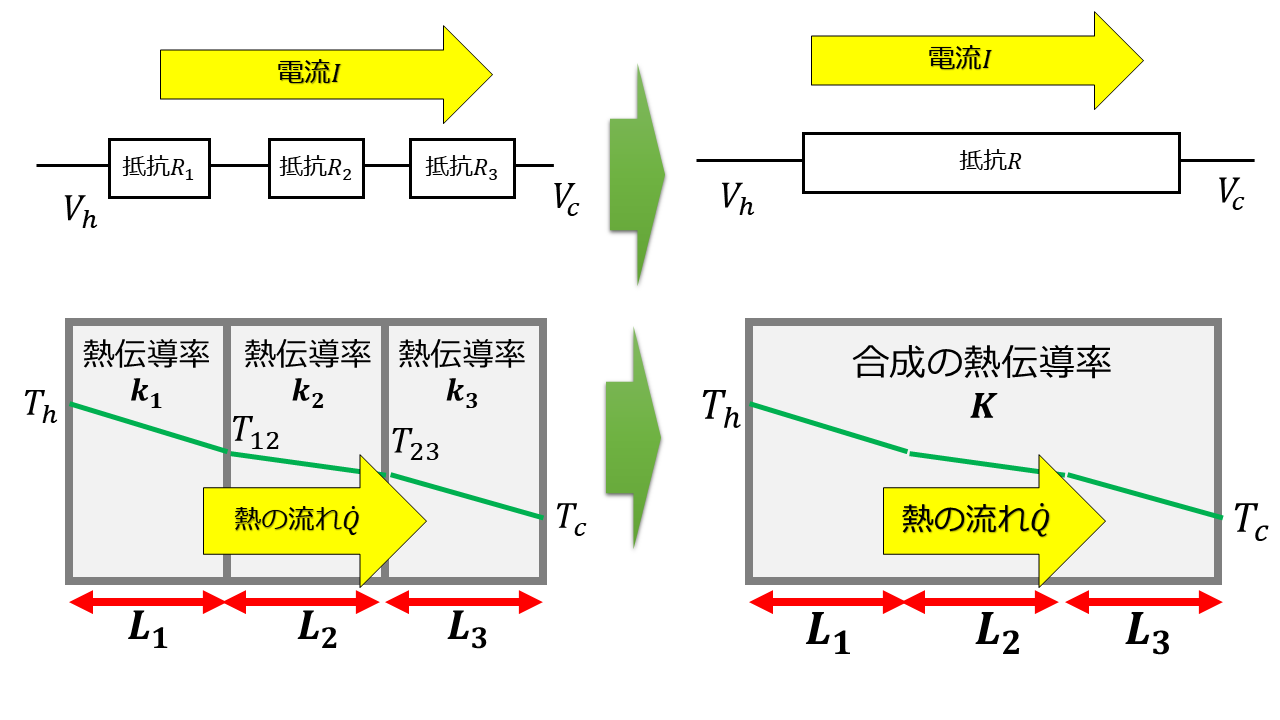
3つの抵抗$R_{1},R_{2},R_{3}$からなる直列回路の合成抵抗は、
R=R_{1}+R_{2}+R_{3}\tag{13}
\end{align*}
となります。
これは、各抵抗を通過する電流が同じで、オームの法則より
- $\Delta V_{1}=R_{1}I$
- $\Delta V_{2}=R_{2}I$
- $\Delta V_{3}=R_{3}I$
となり、ここから$\Delta V=\Delta V_{1}+\Delta V_{2}+\Delta V_{3}=(R_{1}+R_{2}+R_{3})I$より、合成抵抗が(13)のように求まります。
3つの直列回路を3層の熱伝導と類似させて考えることができます。
| 直列回路 | 熱伝導 |
| 電流$I$ | 熱量$\dot{Q}$ |
| 電圧$\Delta V$ | 温度差$\Delta T$ |
| 抵抗$R$ | 熱抵抗$\frac{L}{KA}$ |
このように類似させると、$R_{h}=\frac{L}{KA}$を熱抵抗として、3層の熱伝導率の合成は以下のように直列回路と同じように熱抵抗の和で書くことができます。
\frac{L}{KA}=\frac{L_{1}}{k_{1}A}+\frac{L_{2}}{k_{2}A}+\frac{L_{3}}{k_{3}A}
\end{align*}
まとめ
本記事では3層の熱伝導率の合成について考えました。
今回は3層でしたが、これが$N$層になっても考え方は同じです。
N層の場合の熱伝導率の合成
\frac{L}{KA}&=\frac{L_{1}}{k_{1}A}+\frac{L_{2}}{k_{2}A}+\frac{L_{3}}{k_{3}A}+\cdots + \frac{L_{N}}{k_{N}A}\\
&=\sum_{i=1}^{N}\frac{L_{i}}{k_{i}A}
\end{align*}
※$L=L_{1}+L_{2}+\dots +L_{N}$
以前にFortranを使って熱伝導方程式を解いた記事を書きましたので、興味ある方は覗いてみてください。
おすすめ参考書
伝熱工学の基礎勉強のための参考書と演習問題を紹介します。
Follow @t_kun_kamakiri