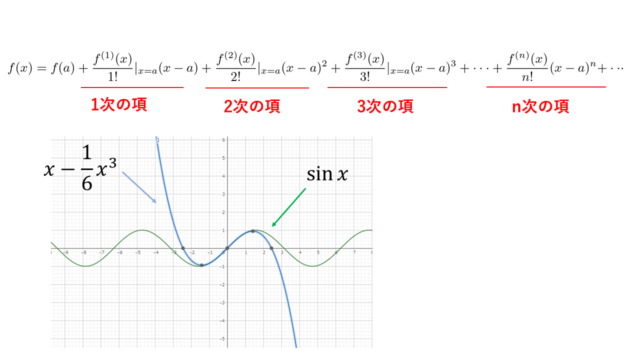
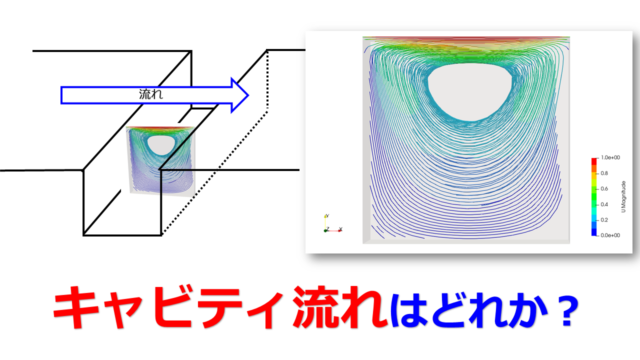
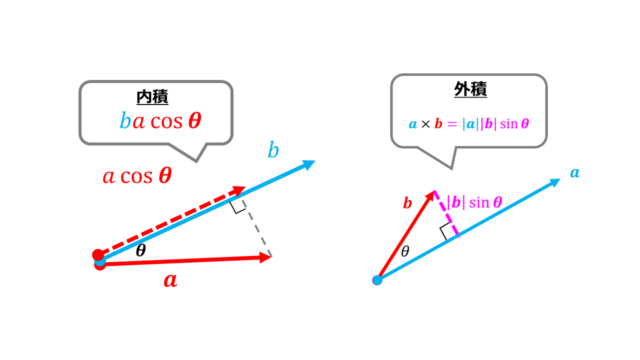
【レイノルズ応力とは】レイノルズ平均モデルでの乱れによるせん断力

こんにちは（@t_kun_kamakiri)

本日は「計算力学技術者試験の熱流体2級」で出てくるレイノルズ応力の解説をします。
レイノルズ応力とは「レイノルズ平均モデルでの乱れ成分のせん断力」です。

と、言われてもおそらく多くの方が、

レイノルズ平均モデルって何？
乱れ成分？
せん断力？

となっていることでしょう。

レイノルズ応力は、特に乱れた流れを数値シミュレーションする際に出てくる用語で、熱流体のCAE解析をする人は必ず知っておく必要があります。

こんな方が対象

計算力学技術者試験の熱流体2級を勉強している方
乱流についての数値的な取り扱いを勉強し始めた方
レイノルズ応力とは何かを知りたい方

※微分や偏微分などは理解している方を対象にしています。

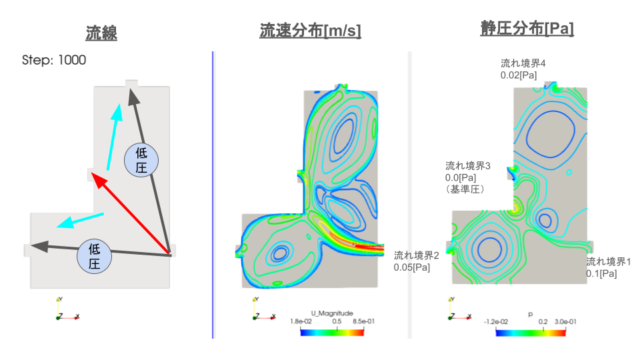
では、問題です。

問題

レイノルズ応力を数式で表しなさい。
レイノルズ応力の意味を説明しなさい。
レイノルズ平均モデルとはどういうモデル化を説明しなさい。

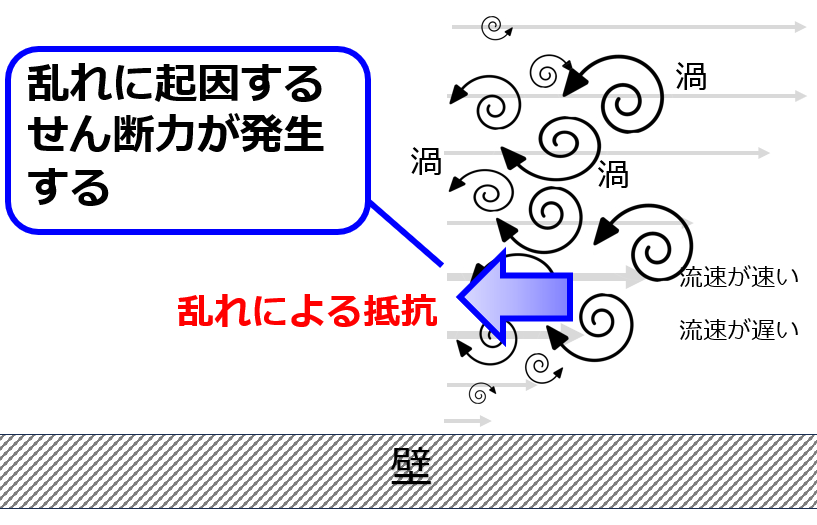
たびたび出てくる絵ですがレイノルズ応力はこんなイメージです。
あとで説明します。

問題の解説は本記事に書いています。
解答はまとめに書いています。

レイノルズ応力について、上記の問題について瞬時に解説ができれば熱流体2級（もしくは1級レベルも）の合格はグッと近づきますね。

レイノルズ応力を数式で表す
レイノルズ応力の意味
1. 分子粘性
2. レイノルズ応力
レイノルズ平均モデル
まとめ
計算力学技術者のための問題アプリ
お勧めの参考書

レイノルズ応力を数式で表す

レイノルズ応力を導出するのは少々道のりが長くなるので、導出は後にしてまずは結果を示します。

レイノルズ応力は以下の式で表されます。

レイノルズ応力

\begin{align*}
\begin{pmatrix}
-\rho \overline{u^{\prime}u^{\prime}}& -\rho \overline{u^{\prime}v^{\prime}} & -\rho \overline{u^{\prime}w^{\prime}}\\
-\rho \overline{v^{\prime}u^{\prime}}& -\rho \overline{v^{\prime}v^{\prime}} & -\rho \overline{v^{\prime}w^{\prime}}\\
-\rho \overline{w^{\prime}u^{\prime}}& -\rho \overline{w^{\prime}v^{\prime}} & -\rho \overline{w^{\prime}w^{\prime}}\\
\end{pmatrix}\tag{1}
\end{align*}

レイノルズ応力は(1)で書かれるということを頭に入れてください。
(1)の意味が全く分からないというのが正直なところでしょう。

順を追って説明するとして、以下のように乱れがあることで発生する抵抗であると考えてよいです。

$u^{\prime},v^{\prime},w^{\prime}$が$x,y,z$方向の乱れの成分になります。
乱れの成分については後で説明します。

これを成分で書くとレイノルズ応力は$-\rho\overline{u^{\prime}_{i}u^{\prime}_{j}}$と書くことができます。
$i$と$j$は1,2,3のいずれかを取ります。

ゆえに、

$u^{\prime}_{1}=u^{\prime}$：$x$方向の乱れ成分
$u^{\prime}_{2}=v^{\prime}$：$y$方向の乱れ成分
$u^{\prime}_{3}=w^{\prime}$：$z$方向の乱れ成分

と書くこともあるため、レイノルズ応力は、

\begin{align*}
\begin{pmatrix}
-\rho \overline{u^{\prime}_{1}u^{\prime}_{1}}& -\rho \overline{u^{\prime}_{1}u^{\prime}_{2}} & -\rho \overline{u^{\prime}_{1}u^{\prime}_{3}}\\
-\rho \overline{u^{\prime}_{2}u^{\prime}_{1}}& -\rho \overline{u^{\prime}_{2}u^{\prime}_{2}} & -\rho \overline{u^{\prime}_{2}u^{\prime}_{3}}\\
-\rho \overline{u^{\prime}_{3}u^{\prime}_{1}}& -\rho \overline{u^{\prime}_{2}u^{\prime}_{2}} & -\rho \overline{u^{\prime}_{3}u^{\prime}_{3}}\\
\end{pmatrix}\tag{2}
\end{align*}

と書くこともあります。

まずは、レイノルズ応力は(1)や(2)の形で書くのだということを覚えておきましょう。

余談ですが、以下の式も参考書によってはレイノルズ応力と言ったりするので、式が(1)(2)と違っていても文脈に応じて「レイノルズ平均モデルでの乱れのせん断力のことか・・・」と思ってください。

$\rho\overline{u^{\prime}_{i}u^{\prime}_{j}}$：マイナス記号がない
$\overline{u^{\prime}_{i}u^{\prime}_{j}}$：$\rho$やマイナス記号がない

※計算力学技術者の熱流体2級の標準問題集は$\overline{u^{\prime}_{i}u^{\prime}_{j}}$をレイノルズ応力と解説しているので、少し混乱するかもしれません。

本来、せん断力とは[Pa]=[N/m2]の単位を持っているので、$-\rho\overline{u^{\prime}_{i}u^{\prime}_{j}}$の形が[Pa]に相当します。マイナスがついていますが、この形で$-\rho\overline{u^{\prime}_{i}u^{\prime}_{j}}>0$となります。

レイノルズ応力の意味

レイノルズ応力の意味はどういうものなのか？
先ほど乱れによる抵抗という風に言いましたが、流体にはそもそも粘性抵抗というものが存在します。それとどう違うのかというのを絵にしてみました。

分子粘性
レイノルズ応力

誤解なきよう先に説明をしておきますが、流体には上記の2つの抵抗があるというわけではありません。
このレイノルズ応力というのは、乱れた流れを数式上で表現した際に渦による抵抗を考慮した際に出てくる数式モデル上の応力のことです。
乱れた流れになると小さな渦まで再現しないといけませんが、数値シミュレーションではどうしても細かい渦は再現しきれないので、計算コストを削減するために「渦の影響は数式で考慮してしまおう」としたことにより出てきた応力がレイノルズ応力です。

分子粘性

通常の流体には粘性があります。
プールの水の中で無抵抗で走り回れる人はいませんよね。
流体は流速が速いところと遅いところがあると、それをもとに戻そうとして力が働きます。
それが粘性抵抗（もしくは分子粘性）と呼ばれる力です。

力と言いましたが、力を面積で割った応力[Pa]=[N/m2]で定義されます。

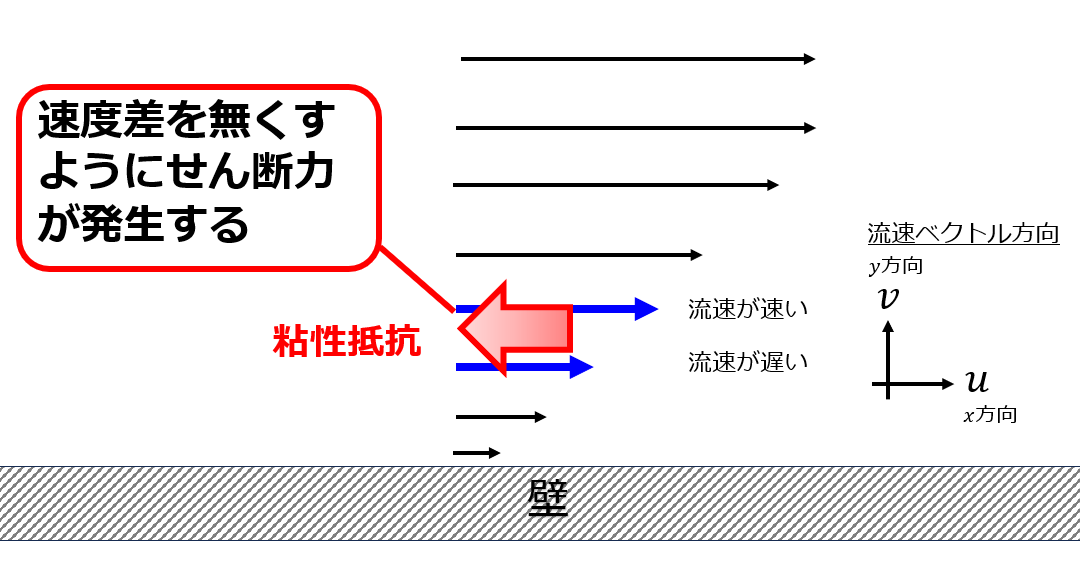
壁では流速は0なので、壁から離れると徐々に速度が大きくなります。
そうすると必ず速度差が出るので、流速差を無くすためにせん断力が働きます。
これが通常の粘性抵抗（分子粘性）です。

そこで$y$方向の$u$($x$方向の流速）の変化量に比例する形でせん断力を定義すると以下のようになります。

\begin{align*}
\tau = \mu \frac{\partial \overline{u}}{\partial y}\tag{3}
\end{align*}

$\mu$：粘性係数
$\overline{u}$：$x$方向の平均流速

※(3)は流速は主に$x$方向に流速がある場合に書きました。

水や空気のような流体は(3)のように速度の空間微分に比例する形で書きましたが、このように線形の関係がある流体を特にニュートン流体といいます。
非線形の関係にある流体を非ニュートン流体といいます。

ニュートン流体か非ニュートン流体かは流体の性質によります。
ニュートン流体の場合は、粘性係数$\mu$が物性値です。

通常の流体による粘性抵抗とは、この速度の空間微分とせん断力で関係付けられる応力のことです。

レイノルズ応力

通常の粘性抵抗の他にどうして乱れに起因するレイノルズ応力を考える必要があるのか、不思議に思うかもしれません。

数値シミュレーションをする際には、連続の空間にぎっしりと点を埋めることはできないので以下のように例えば格子状にして離散的に点を置きます。
このときに、小さな渦というのは格子サイズより小さくなってしまいます。
では、格子サイズをもっと、もっと小さくすればいいということになりますが、これ以上格子サイズを小さくすると格子数が膨大になって計算負荷が大きくなりすぎます。

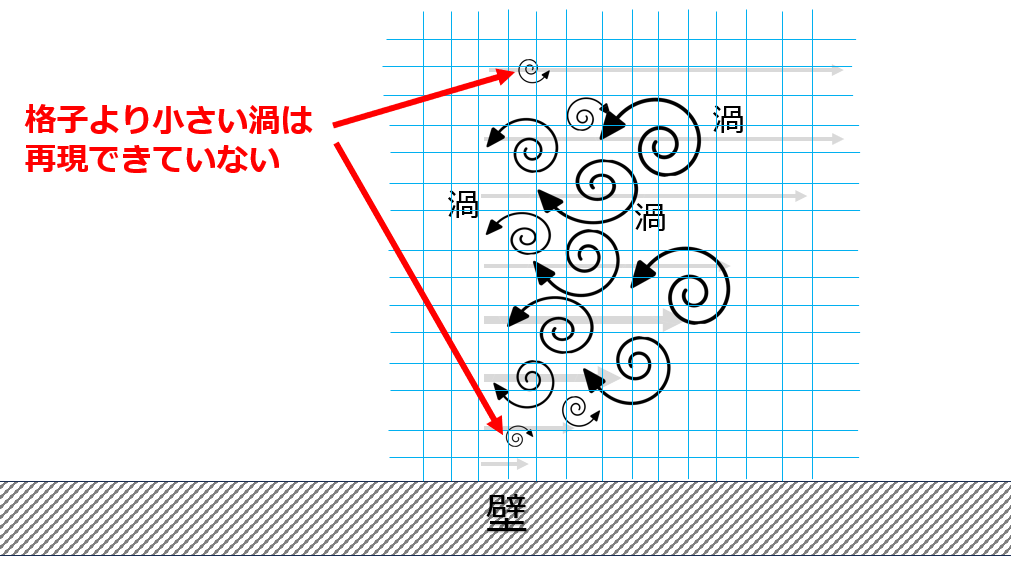
それならばいっそのこと、平均的な流れに乱れの成分を足すことで乱れた流れを数式上で取り込んでしまおうとしたのがレイノルズ平均モデルの考え方です。

平均的な流速を$\overline{\boldsymbol{u}}$で、そこから変動している流速を$\boldsymbol{u}^{\prime}$としたものを乱れた流れにおける流速とします。
圧力についても同様に分解します。

\begin{align*}
\boldsymbol{u}=\overline{\boldsymbol{u}}+\boldsymbol{u}^{\prime}\\
p=\overline{p}+p^{\prime}\tag{4}
\end{align*}

これをレイノルズ分解と言います。

$\boldsymbol{u}^{\prime}$の部分を乱れ流速（乱れ速度）や変動量などと表現しています。

この乱れた流速成分$\boldsymbol{u}^{\prime}$から来るせん断力がレイノルズ応力です。
それゆえ、レイノルズ応力は「レイノルズ平均モデルでの乱れ成分のせん断力」と説明できます。

では、乱れを数式上で取り扱った際に出てくるレイノルズ応力とはどのようにして導出されるのかを次で解説します。

レイノルズ平均モデル

そもそも平均的な流速$\overline{\boldsymbol{u}}$は何を意味しているのか？と思ったことでしょう。

時間的な平均なのか
空間的な平均なのか
アンサンブル平均なのか

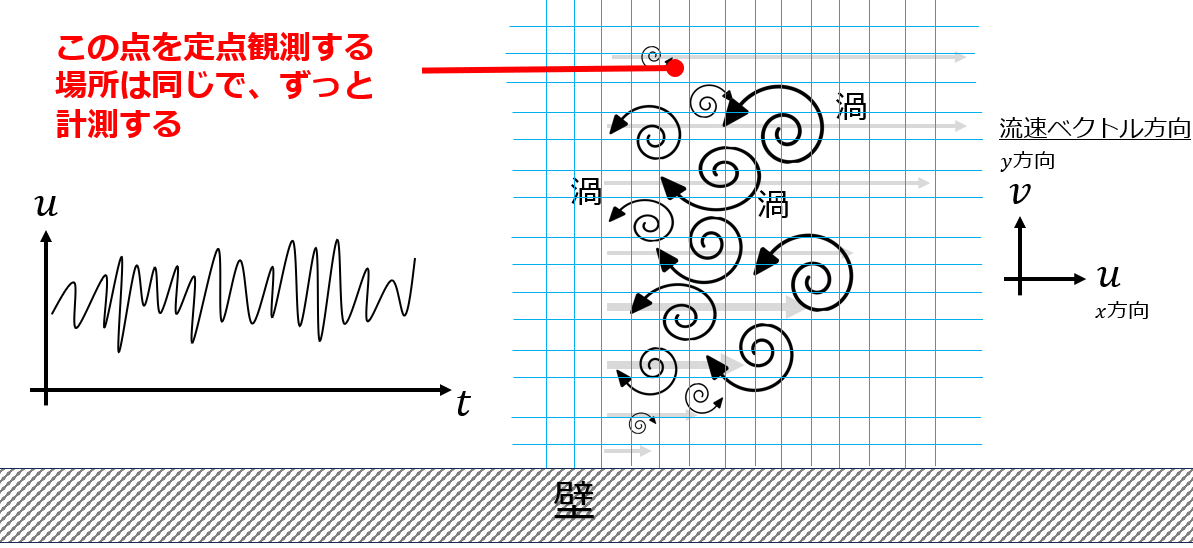
ある点に対して流速を測定して時間平均を行います。
例として$x$方向の流速を測定して、有限の時間で平均することを考えましょう。

\begin{align*}
\overline{u(\boldsymbol{r},t)}=\int^{T}_{0}u(\boldsymbol{r},\tau)\,d\tau
\end{align*}

実際は時間平均した速度に対して乱れ流速$u(\boldsymbol{r},t)^{\prime}$という変動分があるので以下が実際の流速になります。

\begin{align*}
u(\boldsymbol{r},t)=\overline{u(\boldsymbol{r},t)}+u(\boldsymbol{r},t)^{\prime}
\end{align*}

このように時間平均した$\overline{u(\boldsymbol{r},t)}$を使って平均的な流速を求めることで、乱れを考慮した流れの様子を考えようということです。

ここで以下の過程を入れます。

乱れの平均は0：$\overline{u(\boldsymbol{r},t)^{\prime}}=0$
平均と乱れは無相関：$\overline{\overline{u(\boldsymbol{r},t)}u(\boldsymbol{r},t)^{\prime}}=0$
「平均の平均」は平均$\overline{\overline{u(\boldsymbol{r},t)}}=\overline{u(\boldsymbol{r},t)}$

一般的に必ずこうなるとは限らないですが、上式をレイノルズ平均といいます。
一種、こういう過程を入れているわけですね。

ところで、$u(\boldsymbol{r},t)=\overline{u(\boldsymbol{r},t)}+u(\boldsymbol{r},t)^{\prime}$とした場合のナビエストークス方程式はどうなるのでしょうか。

まず、非圧縮性のナビエストークス方程式以下で表されます。

\begin{align*}
\frac{\partial u_{i}}{\partial t}+\frac{\partial u_{i}u_{j}}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial p}{\partial x_{i}}+\nu\frac{\partial^2 u_{i}}{\partial x_{j}^2}+K_{i}\tag{4}
\end{align*}

非圧縮流れにおける連続の式は$\frac{\partial u_{j}}{\partial x_{j}}$となりますが、ここではナビエストークス方程式だけを例にとって考えます。

(4)に$u(\boldsymbol{r},t)=\overline{u(\boldsymbol{r},t)}+u(\boldsymbol{r},t)^{\prime}$を代入します。
計算は次回の記事で詳しく書くとして結果は以下のようになります。

\begin{align*}
\frac{\partial \overline{u_{i}}}{\partial t}+\frac{\partial \overline{u_{i}}\overline{u_{j}}}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}+\nu\frac{\partial^2 \overline{u_{i}}}{\partial x_{j}^2}+\overline{K_{i}}-\frac{\partial \overline{u_{i}^{\prime}{u_{j}^{\prime}}}}{\partial x_{j}}\tag{5}
\end{align*}

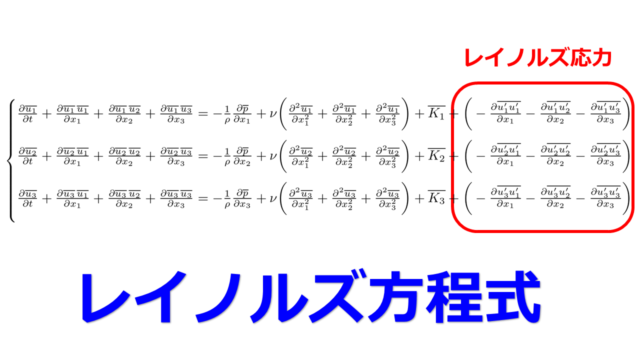
ちゃんと3成分で丁寧に書くと以下となります。

\begin{align*}
\left\{\begin{matrix}
\frac{\partial \overline{u_{1}}}{\partial t}+\frac{\partial \overline{u_{1}}\,\overline{u_{1}}}{\partial x_{1}}+\frac{\partial \overline{u_{1}}\,\overline{u_{2}}}{\partial x_{2}}+\frac{\partial \overline{u_{1}}\,\overline{u_{3}}}{\partial x_{3}}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{1}}+\nu\bigg(\frac{\partial^2 \overline{u_{1}}}{\partial x_{1}^2}+\frac{\partial^2 \overline{u_{1}}}{\partial x_{2}^2}+\frac{\partial^2 \overline{u_{1}}}{\partial x_{3}^2}\bigg)+\overline{K_{1}}+\underset{レイノルズ応力}{\bigg(-\frac{\partial \overline{u_{1}^{\prime}{u_{1}^{\prime}}}}{\partial x_{1}}-\frac{\partial \overline{u_{1}^{\prime}{u_{2}^{\prime}}}}{\partial x_{2}}-\frac{\partial \overline{u_{1}^{\prime}{u_{3}^{\prime}}}}{\partial x_{3}}\bigg)}\\
\frac{\partial \overline{u_{2}}}{\partial t}+\frac{\partial \overline{u_{2}}\,\overline{u_{1}}}{\partial x_{1}}+\frac{\partial \overline{u_{2}}\,\overline{u_{2}}}{\partial x_{2}}+\frac{\partial \overline{u_{2}}\,\overline{u_{3}}}{\partial x_{3}}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{2}}+\nu\bigg(\frac{\partial^2 \overline{u_{2}}}{\partial x_{1}^2}+\frac{\partial^2 \overline{u_{2}}}{\partial x_{2}^2}+\frac{\partial^2 \overline{u_{2}}}{\partial x_{3}^2}\bigg)+\overline{K_{2}}+\underset{レイノルズ応力}{\bigg(-\frac{\partial \overline{u_{2}^{\prime}{u_{1}^{\prime}}}}{\partial x_{1}}-\frac{\partial \overline{u_{2}^{\prime}{u_{2}^{\prime}}}}{\partial x_{2}}-\frac{\partial \overline{u_{2}^{\prime}{u_{3}^{\prime}}}}{\partial x_{3}}\bigg)}\\
\frac{\partial \overline{u_{3}}}{\partial t}+\frac{\partial \overline{u_{3}}\,\overline{u_{1}}}{\partial x_{1}}+\frac{\partial \overline{u_{3}}\,\overline{u_{2}}}{\partial x_{2}}+\frac{\partial \overline{u_{3}}\,\overline{u_{3}}}{\partial x_{3}}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{3}}+\nu\bigg(\frac{\partial^2 \overline{u_{3}}}{\partial x_{1}^2}+\frac{\partial^2 \overline{u_{3}}}{\partial x_{2}^2}+\frac{\partial^2 \overline{u_{3}}}{\partial x_{3}^2}\bigg)+\overline{K_{3}}+\underset{レイノルズ応力}{\bigg(-\frac{\partial \overline{u_{3}^{\prime}{u_{1}^{\prime}}}}{\partial x_{1}}-\frac{\partial \overline{u_{3}^{\prime}{u_{2}^{\prime}}}}{\partial x_{2}}-\frac{\partial \overline{u_{3}^{\prime}{u_{3}^{\prime}}}}{\partial x_{3}}\bigg)}
\end{matrix}\right.
\end{align*}

これをレイノルズ方程式といいます。
これがRANS(Reynolds-Averaged Navier-Stokes)と呼ばれる乱流モデルです。

ナビエストークス方程式と似たような平均流速における式がまた出てきました。
どこが違うのかというと、$-\frac{\partial \overline{u_{i}^{\prime}{u_{j}^{\prime}}}}{\partial x_{j}}$といった余分な項が出ている点です。

これがレイノルズ応力の部分です。
特に密度$\rho$をかけて、通常の粘性と一緒にまとめると

\begin{align*}
\frac{\partial}{\partial x_{j}}\bigg(\underset{通常の粘性（分子粘性)}{\mu\frac{\partial \overline{u_{j}}}{\partial x_{j}}}\,\,\,\,\underset{レイノルズ応力}{-\rho\overline{u_{i}^{\prime}{u_{j}^{\prime}}}}\bigg)\tag{6}
\end{align*}

※$\nu=\frac{\mu}{\rho}$

$-\rho\overline{u_{i}^{\prime}u_{j}^{\prime}}$が乱れ成分に起因するせん断応力であることがわかります。

レイノルズ応力を行列でまとめると、

レイノルズ応力

になるというわけです。

まとめ

少し数式がごちゃごちゃしましたが、レイノルズ応力のお気持ちをわかってもらえれば細かい式については徐々になれてくるので理解できなくても心配する必要はありません。

では、問題の解答です。

問題

レイノルズ応力を数式で表しなさい。
レイノルズ応力の意味を説明しなさい。
レイノルズ平均モデルとはどういうモデル化を説明しなさい。

レイノルズ応力は、

レイノルズ応力

もしくは、

$u^{\prime}_{1}=u^{\prime}$：$x$方向の乱れ成分
$u^{\prime}_{2}=v^{\prime}$：$y$方向の乱れ成分
$u^{\prime}_{3}=w^{\prime}$：$z$方向の乱れ成分

と書く場合は、

レイノルズ応力は「レイノルズ平均モデルでの乱れ成分のせん断力」です。
こんな絵をイメージすればいいですね。

レイノルズ平均モデルとは平均した量と変動量に分解（レイノルズ分解）して

\begin{align*}
\boldsymbol{u}=\overline{\boldsymbol{u}}+\boldsymbol{u}^{\prime}\\
p=\overline{p}+p^{\prime}\tag{4}
\end{align*}

以下のレイノルズ平均を仮定して

乱れの平均は0：$\overline{u(\boldsymbol{r},t)^{\prime}}=0$
平均と乱れは無相関：$\overline{\overline{u(\boldsymbol{r},t)}u(\boldsymbol{r},t)^{\prime}}=0$
「平均の平均」は平均$\overline{\overline{u(\boldsymbol{r},t)}}=\overline{u(\boldsymbol{r},t)}$

以下のレイノルズ方程式で考えるモデル化のことです。

これがRANS(Reynolds-Averaged Navier-Stokes)と呼ばれる乱流モデル。

これくらいサラッと語れるようになればOKです。

レイノルズ方程式を導出しましたが、ところでレイノルズ応力$-\rho\overline{u_{i}^{\prime}u_{j}^{\prime}}$はわかっているものでしたっけ？
実はまだ未知の量です。

さらに、このレイノルズ応力$-\rho\overline{u_{i}^{\prime}u_{j}^{\prime}}$をどのようにモデル化するかで色々な乱流モデルが提案されているわけです。