こんにちは(@t_kun_kamakiri)
今回の記事では2次元の円柱まわりの流れの流体解析の設定方法を示します。
2025年5月末の技術書典18に向けて、OpenFOAMを用いた熱流体解析のひとつのテーマとして円柱まわりの流れを考えています。
- OpenFOAMで使用できる熱流体解析ソルバ
- 熱流体の理論式の理解
【宣伝】2次元円柱内流れ(非圧縮流れ)
本代に入る前に少し宣伝ですが・・・メッシュ作成方法は技術書典17で販売している技術書に書いている方法を使用しています。
さらに技術書典17では以下の「2次元円柱内流れ(非圧縮流れ)」として、
- カルマン渦の生成
- レイノルズ数と抗力係数の関係
- レイノルズ数とストローハル数
- ポテンシャル流れと粘性流体の圧力係数の違い
- 力学的相似性
- Pythonを使ったパラメータスタディ
などなど、モデル作成からグラフ作成までの一連の流れをまとめたものを出しております。
ページ数は140ページです。
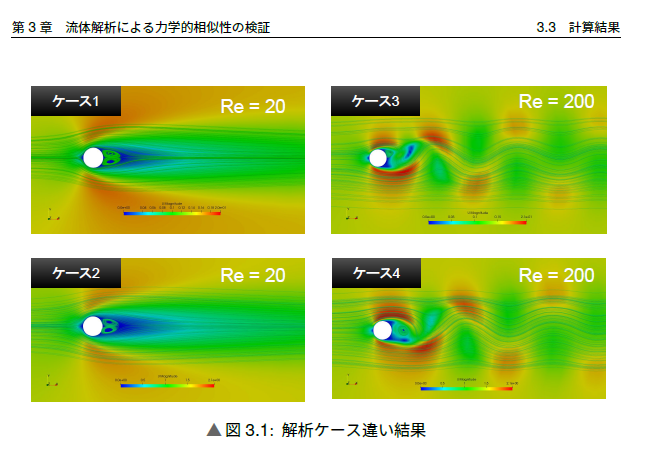
↓内容のチラ見せ
本書の解析モデルはgithubに置いているので、本書と照らし合わせながら読み進めることができます。
興味ある方はぜひ手に取ってみてください。
熱流体解析
熱流体というと温度を扱う方程式を追加していることが特徴になります。
例えば、非圧縮流れであると変数は$\boldsymbol{v}, p$の2つなので、質量保存則と運動量保存則(運動方程式)だけで完結します。
そのため、温度を扱う必要がないため、「温度がどうなのか?」という議論は出てきません。

これは、質量保存則$\frac{\partial \rho}{\partial t}+\nabla\cdot (\rho\boldsymbol{v})=0$から密度一定から、$\nabla \cdot \boldsymbol{v}=0$の非圧縮条件により、密度を考えなく良いためでもあります。
流体の基礎式(一般式)を書くと以下のようになり、マッハ数が0.3以上で密度変化が5%程度になるため、決して無視することができなく、以下の4つの式を解く必要が出てきます。

OpenFOAMの熱流体ソルバ
| ソルバ名 | 対象 | 圧縮性 | 特徴・用途 |
|---|---|---|---|
buoyantBoussinesqPimpleFoam |
非圧縮 | ✖(Boussinesq近似) | 密度変化を温度差に限定(小さい温度差向け) |
buoyantSimpleFoam |
定常 / 非圧縮 | ✖(Boussinesq or 温度依存) | 非圧縮性の定常熱対流解析(自然・強制) |
buoyantPimpleFoam |
非定常 / 非圧縮 | ✖(温度依存密度) | 非圧縮性の非定常熱流体解析(自然対流、時間変化あり) |
chtMultiRegionSimpleFoam |
定常 / 多領域 | ✖ | 固体と流体の定常熱連成解析(伝熱・熱交換器など) |
chtMultiRegionFoam |
非定常 / 多領域 | ✖ | 固体-流体の非定常熱連成解析(電子冷却、接触伝熱) |
rhoSimpleFoam |
定常 / 圧縮 | ✔ | 低速~中速の圧縮性流体+熱伝導(定常) |
rhoPimpleFoam |
非定常 / 圧縮 | ✔ | 非定常かつ圧縮性熱流体問題(高マッハ、衝撃波) |
sonicFoam |
非定常 / 圧縮 | ✔ | 音速以上の圧縮性熱流体(超音速、燃焼) |
reactingFoam |
燃焼 / 圧縮 | ✔ | 化学反応を伴う燃焼・熱流体問題 |
reactingParcelFoam |
噴霧 / 燃焼 | ✔ | 液滴(Lagrangian)を含む燃焼問題 |
こうした温度や密度の変化を扱う際に使用するのが、OpenFOAMのbuoyantPimpleFoamソルバーです。
buoyantPimpleFoam は、以下のような問題に適しています:
– 自然対流や強制対流を含む熱流体問題
– 密度が温度に依存するモデル
– 非圧縮性仮定 + 熱浮力効果を含むケース
このソルバーが扱う方程式は次のとおりです。
– $\nabla \cdot \boldsymbol{v} = 0$ (非圧縮性の連続式)
– 運動量保存式(浮力項付きNavier-Stokes)
– エンタルピー保存式(熱の拡散と輸送)