角運動量保存則：回転対称（ネーターの定理）

とても久しぶりに解析力学をやっております(笑)

前回、並進対称性（空間等方性）なら運動量保存則が成り立つというのを見ました。

また、ちょっと復習です。

ネーターの定理
「系に連続的な対称性がある場合はそれに対応する保存則が存在する」と述べる定理である。
ドイツの数学者エミー・ネーターによって1915年に証明され、1918年に公表された。

解析力学や場の理論における重要な定理であります。

これだけ覚えておけば良いでしょう(^^)/

「対称性が何によるかによって保存則が決まっている」という理解です。

対称性	保存則
時間対称性	エネルギー保存則
並進対称性	運動量保存則
回転対称性	角運動量保存則（モーメントの保存）
ゲージ対称性（位相変換）	電荷保存則

今回は、回転対称性（空間等方性）なら角運動量保存則が存在するといのを見ていこうと思います(^^)/

では、やっていきましょう♪

回転対称性（空間等方性）⇔角運動量保存則
1. ラグランジアンの変分
2. \(\delta r_{a}\)、\(\delta v_{a}\)の計算
まとめ
参考図書

回転対称性（空間等方性）⇔角運動量保存則

さて、空間等方性であるということをラグランジアン\(L\)に課しましょう。

すると、どんな保存量が出てくるかを見ていこうと思います。

空間等方性ってどんなイメージなのかを見た方が良さそうですね。

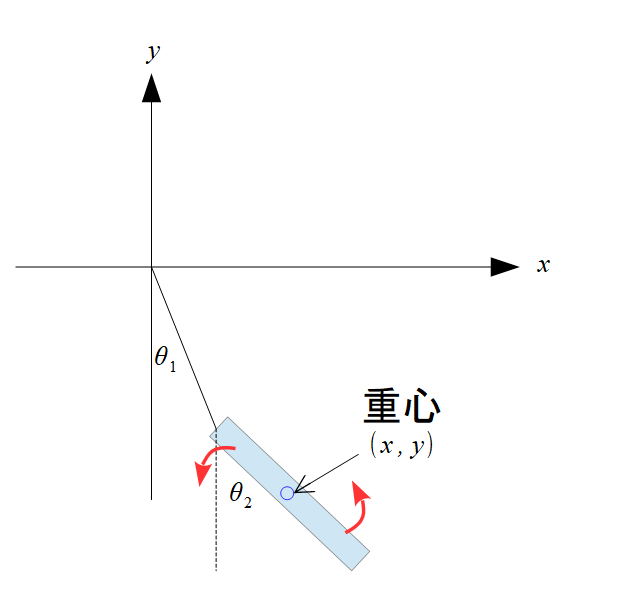
こんな感じです。

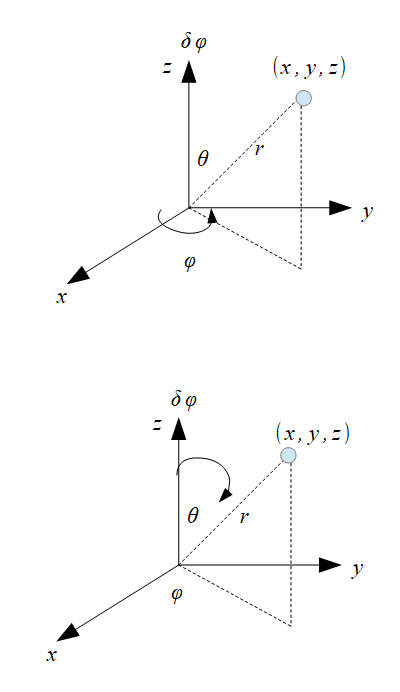
〇の座標は、

デカルト座標

\((x,y,z)\)

球座標

\((r,\phi,\theta)\)

\(x=r\sin\phi\cos\theta\)
\(y=r\sin\phi\sin\theta\)
\(x=r\cos\theta\)

となりますね。

空間等方性というのは、ここで例えばスカラー量\(f\)というのを考えた時、一般的には\(f(r,\phi,\theta)\)と、\(r,\phi,\theta\)に依るのですが、\(\phi,\theta\)の回転方向には依存しないと言う意味です。

ここで考えたいのは、系全体を微小回転\(\delta\phi \)させた時に、ラグランジアン\(L\)が変わらない場合です。

言い換えると、「任意の回転によって空間内での系全体としての（孤立した）力学系性質が変わらない」という場合を考えたいのです。

回転させる回転軸ですが、空間等方性を仮定しているのでどこを軸にとっても良いでしょう。

ここでは、便宜上\(z\)軸にしておきます。

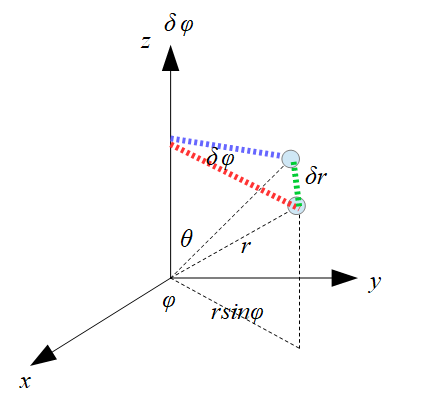
こんな感じで、z軸の周りに微小回転\(\delta \phi\)をさせた場合を考えます。

赤の点線から青の点線まで系を回転させました。

z軸周りの回転を考えていますが、微小回転を\(\delta \phi\)と置いているので、回転軸も\(\delta \phi\)と置いておきます。

あとで、ベクトル表記で考えたいので・・(^^)

ラグランジアンの変分

位置が赤の点線上だったのが、青の点線上になったのですから、系全体の回転によって位置も速度それぞれ、\(\delta r\)、\(\delta v\)だけ変わっています。

なので、\(L\)の変分は、

\begin{align*}\delta L=L(r_{1}+\delta r_{1},r_{2}+\delta r_{2},\cdot\cdot\cdot,v_{1}+\delta v_{1},v_{2}+\delta v_{2},\cdot\cdot\cdot )-L(r_{1},r_{2}\cdot\cdot\cdot,v_{1},v{2},\cdot\cdot\cdot )\cdot\cdot\cdot (1)\end{align*}

これは散々今までにやりましたので、(1)式があっさり次のようになることがわかります。

\begin{align*}\delta L=\sum_{a}\big(\frac{\partial L}{\partial \boldsymbol{r}_{a}}\cdot\delta\boldsymbol{r}_{a}+\frac{\partial L}{\partial \boldsymbol{v}_{a}}\cdot\delta\boldsymbol{v}_{a}\big)\cdot\cdot\cdot (2)\end{align*}

回転に対してラグランジアンが不変ということなので、

変分\(\delta L=0\)を課して、

\begin{align*}\sum_{a}\big(\frac{\partial L}{\partial \boldsymbol{r}_{a}}\cdot\delta\boldsymbol{r}_{a}+\frac{\partial L}{\partial \boldsymbol{v}_{a}}\cdot\delta\boldsymbol{v}_{a}\big)=0\cdot\cdot\cdot (3)\end{align*}

となります。
※\(a\)は自由度分だけ足し合わせてください。

さて、\(\delta r_{a}\)、\(\delta v_{a}\)はどのように書けますでしょうか？

\(\delta r_{a}\)、\(\delta v_{a}\)の計算

\(\delta \phi\)軸側から見たらわかりやすいですね。

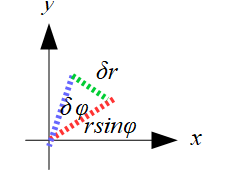
\begin{align*}|\delta r|=r\sin\theta\delta\phi\end{align*}

このようになりますね。

ここで、ちょっと見方を変えて・・・・・・

これは外積を行っているのと同じになります。

要するに、「下記のように赤色の細い点線から赤色のい太点線へ変換して掛け算しているようなもの」です。

そしてその掛け算には向きがあって、緑色の点線の方向（回転方向）になります。
右ねじの法則ですね。

これが外積です。

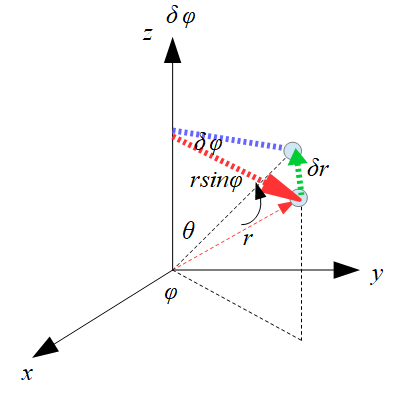
式で書くと・・・

\begin{align*}\delta \boldsymbol{r}=\delta \boldsymbol{\phi}\times\boldsymbol{r}\cdot\cdot\cdot (4)\end{align*}

速度についても変化します（すべての粒子の速度が変化します）。
(4)式より、

\begin{align*}\delta \boldsymbol{v}=\delta \boldsymbol{\phi}\times\boldsymbol{v}\cdot\cdot\cdot (5)\end{align*}

となります。

(3)式に、(4)(5)を代入すると・・・

\begin{align*}\sum_{a}\bigg(\frac{\partial L}{\partial \boldsymbol{r}_{a}}\cdot\big(\delta \boldsymbol{\phi}\times\boldsymbol{r}_{a}\big)+\frac{\partial L}{\partial \boldsymbol{v}_{a}}\cdot\big(\delta \boldsymbol{\phi}\times\boldsymbol{v}_{a}\big)\bigg)=0\end{align*}

さらに、

ラグランジュ方程式

\begin{align*}\frac{d}{dt}\frac{\partial L}{\partial \boldsymbol{v}_{a}}=\frac{\partial L}{\partial \boldsymbol{r}_{a}}\end{align*}

>>ラグランジュ方程式

運動量

\begin{align*}\boldsymbol{P}=\frac{\partial L}{\partial \boldsymbol{v}_{a}}\end{align*}

>>運動量

であることに注意すると、

\begin{align*}\sum_{a}\bigg(\dot{\boldsymbol{P}}\cdot\big(\delta \boldsymbol{\phi}\times\boldsymbol{r}_{a}\big)+\boldsymbol{P}\cdot\big(\delta \boldsymbol{\phi}\times\boldsymbol{v}_{a}\big)\bigg)=0\cdot\cdot\cdot (6)\end{align*}

このようになりました(^^)

ここでベクトル公式のスカラー3重積を用います。

スカラー3重積というのは、こんな感じです。

\begin{align*}\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C})=\boldsymbol{B}\cdot(\boldsymbol{C}\times\boldsymbol{A})=\boldsymbol{C}\cdot(\boldsymbol{A}\times\boldsymbol{B})\end{align*}

詳しい説明は、こちらの方がよろしいです↓
http://hooktail.sub.jp/vectoranalysis/Triprod/

(6)式から、\(\delta \boldsymbol{\phi}\)をくくりだしてやります。

上の公式を見ながらします。

\begin{align*}\sum_{a}\bigg(\delta \boldsymbol{\phi}\cdot\big(\boldsymbol{r}_{a}\times\dot{\boldsymbol{P}}\big)+\delta \boldsymbol{\phi}\cdot\big(\boldsymbol{v}_{a}\times\boldsymbol{P}\big)\bigg)=0\end{align*}

⇔

\begin{align*}\delta \boldsymbol{\phi}\cdot\sum_{a}\bigg(\big(\boldsymbol{r}_{a}\times\dot{\boldsymbol{P}}\big)+\big(\boldsymbol{v}_{a}\times\boldsymbol{P}\big)\bigg)=0\end{align*}

⇔

\begin{align*}\delta \boldsymbol{\phi}\cdot\sum_{a}\frac{d}{dt}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)=0\end{align*}

⇔※微分と和は入れ替えれる

\begin{align*}\delta \boldsymbol{\phi}\cdot\frac{d}{dt}\sum_{a}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)=0
\cdot\cdot\cdot (7)\end{align*}

とこのようになりました(^^)/

やっとここまできました(^^)

ここで、任意の微小回転\(\delta \phi\)に対して(7)式が恒等的に成り立つということは、

\begin{align*}\frac{d}{dt}\sum_{a}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)=0
\cdot\cdot\cdot (8)\end{align*}

ここで、

\begin{align*}\boldsymbol{M}=\sum_{a}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)
\cdot\cdot\cdot (9)\end{align*}

とおけば、(8)式より

\begin{align*}\frac{d\boldsymbol{M}}{dt}=0
\cdot\cdot\cdot (9)\end{align*}

すなわち、\(\boldsymbol{M}\)が保存することになります。

\begin{align*}\boldsymbol{M}=\sum_{a}\big(\boldsymbol{r}_{a}\times\boldsymbol{P}\big)\end{align*}

は何でしょうか？

思いっきり角運動量を表していますね(笑)

まとめ

系全体を微小回転\(\delta\phi\)だけ回転させても、ラグランジアン\(L\)が変わらない（空間等方性）ということを要請すると、

\begin{align*}\frac{d\boldsymbol{M}}{dt}=0
\cdot\cdot\cdot (9)\end{align*}

すなわち、角運動量\(\boldsymbol{M}\)が保存する。

ネーターの定理

「対称性が何によるかによって保存則が決まっている」

対称性	保存則
時間対称性	エネルギー保存則
並進対称性	運動量保存則
回転対称性	角運動量保存則（モーメントの保存）
ゲージ対称性（位相変換）	電荷保存則