本日は、位相空間のお話をしたいと思います(^^)/
位相空間というと数学で言うところのトポロジーとか、そっち系の話でも出てきますが、ここでの位相空間はそれではありません(笑)
英語で言うと、
- phase space:位相空間(相空間とも言います)👈本日のお話
- topological space:位相空間
と区別されます。
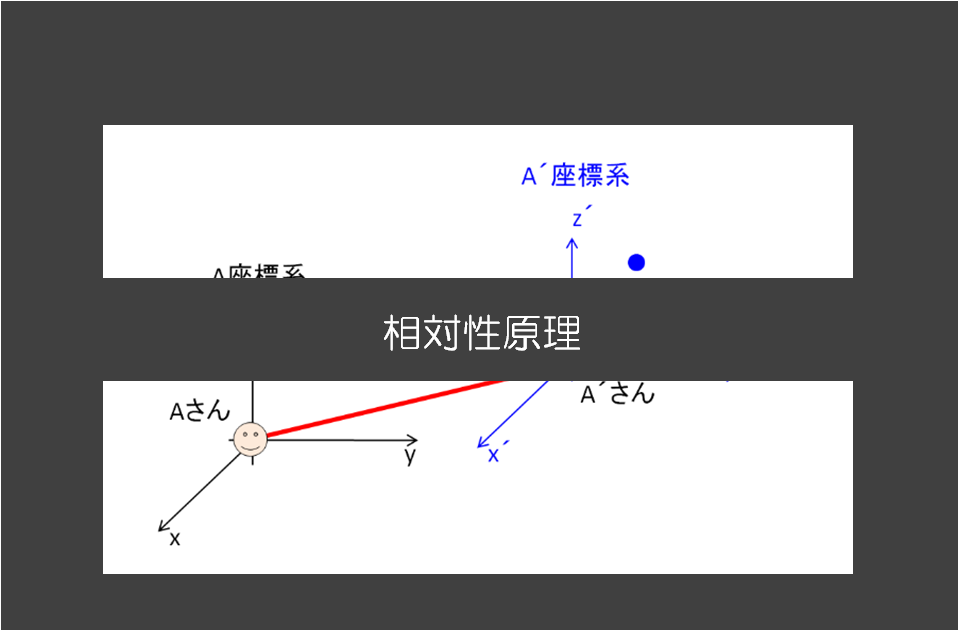
力学的な状態を決める力学変数は「座標と」「運動量」
<力学的な状態>を決める変数は何であったかというお話からします。
状態を決めるのに、どんな変数を使えばよいのでしょうか。
●が何か粒子であると見てください。
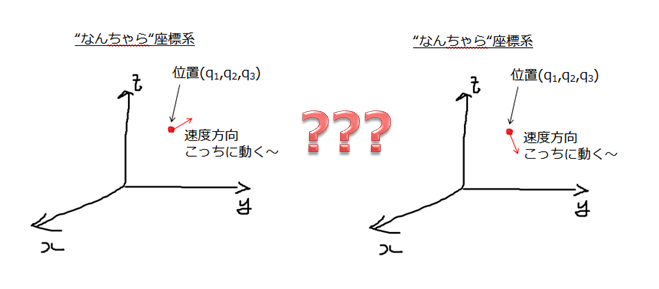
この絵を見てお分かりの通り、位置だけ決めても力学的な状態というのは決定できていません(次の運動を予測できない)。
なぜなら、次の時刻にどこに行くかを指定していないからです。
つまり、位置という変数以外に速度という変数が必要です。
「なるほど、<力学的な状態>を決定する変数は、座標と速度が必要なのか」とこのように納得できます(^^)/
ただ、座標と速度を指定することが変数としての選び方の全てではないことを当ブログでは書きました。
それは、座標と運動量を変数としても良いということです。
<<力学的状態>>を決めるのに、力学変数を一般座標\(q_{i}\)、一般運動量\(p_{i}\)として、ハミルトニアン\(H(\{q_{i}\},\{p_{i}\},t)\)を考えれば良いことになります。
ハミルトニアンは時間変化するのか?
ところで、ハミルトニアン\(H(\{q_{i}\},\{p_{i}\},t)\)は時間に依存するのか?
と、言うことが気になります。
\(\{q_{i}\},\{p_{i}\}\)を変数に持つときを特にハミルトニアンと呼んでいました。
正準形式のエネルギ関数というものです。
つまりエネルギーです。
エネルギー保存を考えた時、エネルギーは変化しないですよね。
何に対して変化しないのか?
それは、時間に関して変化しないのですよね。
だから、ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)(\(t\)は消した)は時間に依存しないはずなんです。
でもこれは自明なことではありません。
ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)の変数は\(q_{i}\)や\(p_{i}\)ですが、これらも時間依存しているのです。
つまり、ハミルトニアンは\(H(\{q_{i}(t)\},\{p_{i}(t)\})\)と、こう書くべきなのです。
\(q_{i}(t)\)や\(p_{i}(t)\)が時間に対して様々な値をとるので、
同じ\(q_{i}\)や\(p_{i}\)の値であってもハミルトニアンの値は異なるように思えますが、
同じ\(q_{i}\)や\(p_{i}\)であればハミルトニアンが同じであるということになるのです。
これが、ハミルトニアンが時間に陽に依存しないという意味です。
一般的に、関数(ここでは温度場としましょうか)\(T(x(t),t)\)と書くと、
同じ位置の温度を測定していても時間によって変化します。
(変化しても良くて、変わらないという制限はない)
それに、\(T(x(t))\)と書いても、測定位置を変えれば温度だって変わります。
(変わってはいけないという制限はない)
本当かいな?(笑)
前段が長くなりましたが、↑それを見てみましょう(^^)/
ハミルトニアンの常微分\(\frac{dH}{dt}\)は?
では、ハミルトニアン\(H(\{q_{i}\},\{p_{i}\},t)\)の時間微分を考えてみましょう。
}\frac{dp_{i}}{dt}\big)
\cdot\cdot\cdot (1)\end{align*}
※もし、全微分と偏微分が「ん?」って人は↓こちらをどうぞ(^^)/
ここで、ハミルトンの正準方程式
\cdot\cdot\cdot (2)\end{align*}
\cdot\cdot\cdot (3)\end{align*}
より、①の第二項の括弧の中で使いましょう。
}\frac{\partial H}{\partial q_{i}}\big)
\cdot\cdot\cdot (4)\end{align*}
すると、よく見ると第二項の括弧の中が0であることがわかります。
したがって、
\cdot\cdot\cdot (4)\end{align*}
となるのです。
何か右辺も左辺も同じように見えますが、意味は違います。
右辺:\(q_{i}(t)\)と\(p_{i}(t)\)を固定して(ある値に決めて)時間微分
左辺:任意の\(q_{i}(t)\)と\(p_{i}(t)\)に対しての時間微分
ハミルトニアンが時間に陽に依存しないのであれば、④より任意の\(q_{i}(t)\)と\(p_{i}(t)\)に対してハミルトニアンは一定であることが言えます。
すなわち、
\cdot\cdot\cdot (5)\end{align*}
これがエネルギー保存です。
位相空間で理解しよう
というわけでようやく位相空間のところの話ができます(笑)
もう一度言いますが、ハミルトニアンが時間に陽に依存しないとは絵で書くとこんな感じです。
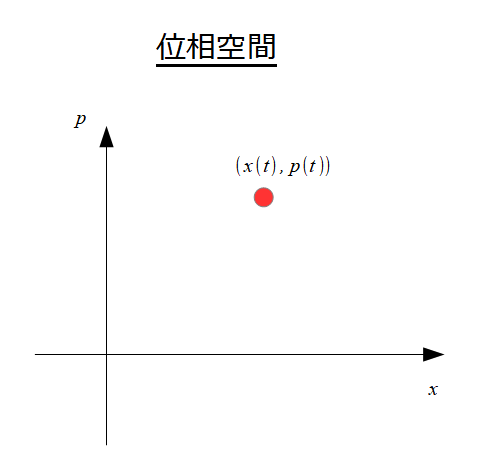
「ある(位置、運動量)=\(x(t),p(t)\)を時間変化させてず~と眺めていても、ハミルトニアンは変わらないよ」
って言うのが、ハミルトニアンが時間に陽に依存しないという意味です。
※上の絵だと状態点の一点をずっと眺めている感じで、そりゃ~ハミルトニアンは変わらないでしょうねって感じです(笑)
⑤式は何を意味しているのかと言いますと、

上の絵のように、「始めに決めた(位置、運動量)=\(\big(x(t_{1}),p(t_{1})\big)\)によるハミルトニアンの値は、時間変化しても(位置、運動量)=\(\big((x(t),p(t)\big)\)の値は変わるのですが、ハミルトニアンの値は変わらないよ」
っていうのが(5)式の意味です。
つまり、「初期状態でのエネルギーが保存されている」ということです。
そして、このように位置と運動量で力学的な状態を表現する空間を物理学では位相空間と言います。
位相空間上の●を状態点と言います。
では簡単な例で、位相空間を使って考えてみましょう(^^)/
単振動を位相空間を使って考える

このようにおもりの質量が\(m\)で、バネ(バネ定数\(k\))につながれていて、自然長から距離\(x\)だけ引き伸ばすと単振動しますよね。
その時のエネルギーはよく知られているように、
\cdot\cdot\cdot (6)\end{align*}
と書けます。
変数を座標\(x\)と運動量\(p=m\dot{x}\)として、ハミルトン形式で書いておきましょうか。
\cdot\cdot\cdot (7)\end{align*}
そしてエネルギー保存より、単振動の場合は位相空間上で状態点が楕円軌道を描くことになります。
(7)式を式変形すると、
\cdot\cdot\cdot (8)\end{align*}
となります。
ここで、\(\omega=\frac{k}{m}\)(振動数)とおきました。
さて、これは楕円の方程式\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)と全く同じ形をしています。
(8)式の位相空間上での状態点の軌跡を書くと、
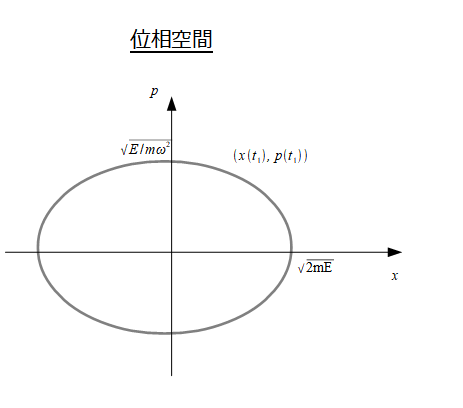
こんな感じです(^^)/
これが単振動の場合の、位相空間上での状態の移り変わりです。
\(E\)は初期に蓄えていた全エネルギーです。
例えば、バネを自然長から\(x=x_{0}\)だけ伸ばせば、
全エネルギーは\(E=\frac{1}{2}kx_{0}^2\)となります。
単振動の楕円を円に変えれないか?
単振動の位相空間上の状態点の軌跡を描きましたが、どうでしょう?
正直、僕は楕円より円の方がきれいだなって思いました(笑)
実は、楕円を円に変換することができるのです(^^)/
やったー♪
ですが、まだ僕にはその手段を持っていません(笑)
これは、「正準変換」と「リウヴィリの定理」をしっかり学んでから示したいと思います(‘;’)
まとめ
本日学んだのは2点です。
1.ハミルトニアンが時間に陽に依存しないのであれば、(4)式より任意の\(q_{i}(t)\)と\(p_{i}(t)\)に対してハミルトニアンは一定である
\cdot\cdot\cdot (5)\end{align*}
2.位置と運動量で力学的な状態を表現する空間を物理学では位相空間と言います。
位相空間上の●を状態点と言います。
次回
それでは、次回はいよいよ正準変換のお話をしようかと思います!(^^)!
さ~てこの辺から学生時代にあまりちゃんと勉強してなかったぞ~って感じです(笑)
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。





























解析力学についてググりまくってたらここに辿り着きました。
図が多い、かつ他のアフィブログと違い大切なところが省略されていないので大変分かりやすいです。
お読み頂いてありがとうございます。
図とストーリー(自分の思考)は大切にしていこうと考えています。
アフィブログとしてもやっているのでその点はご了承くださいm(_ _)m
まだまだ勉強しながら書いている身であるので間違いや勘違いで書いている場合もあるかもしれませんが、お気づきの点ありましたら教えて頂ければ幸いです。
コメントありがとうございました。