どうも(@t_kun_kamakiri)(‘◇’)ゞ
本記事では、グロス・ピタエフスキー方程式の極座標表示について解説したいと思います。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi(\boldsymbol{r})+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{1}
\end{align*}
※↑デカルト座標での表記
なぜ、グロス・ピタエフスキー方程式の極座標表示をするのかというと、この後(別の)記事で量子渦の構造について考えていきたいと思っているからです。
なぜ、極座標表示で方程式を書きなおしたいかは本記事内で解説します。
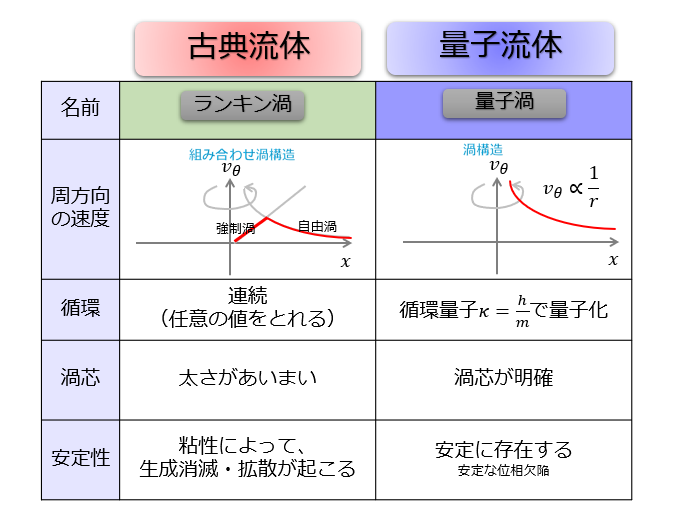
「低温状態で出現するボースアインシュタイン凝縮による流体(量子流体)の渦のことを量子渦と呼ばれています。」
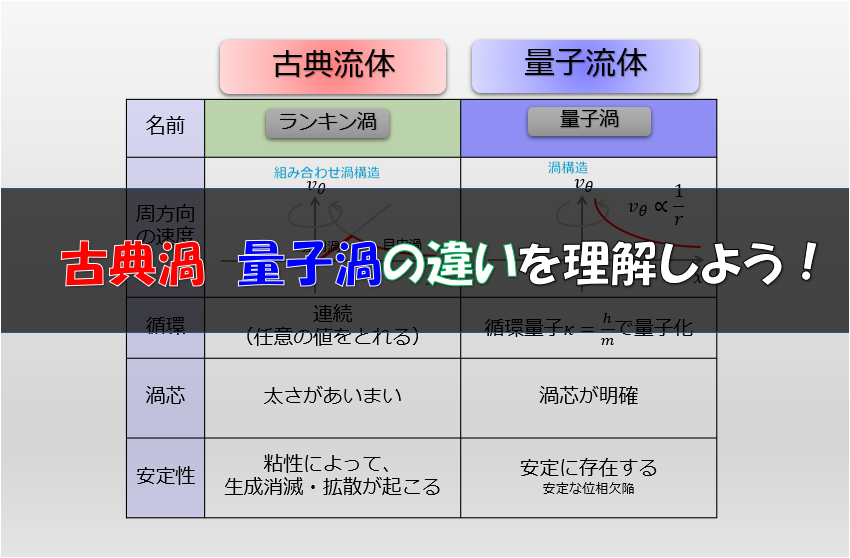
通常の渦と、量子渦との違いについては下記の記事をご参考ください。
表で「古典渦」と量子渦の違いを以下にまとめておきます。

グロス・ピタエフスキー方程式を極座標表示で考える
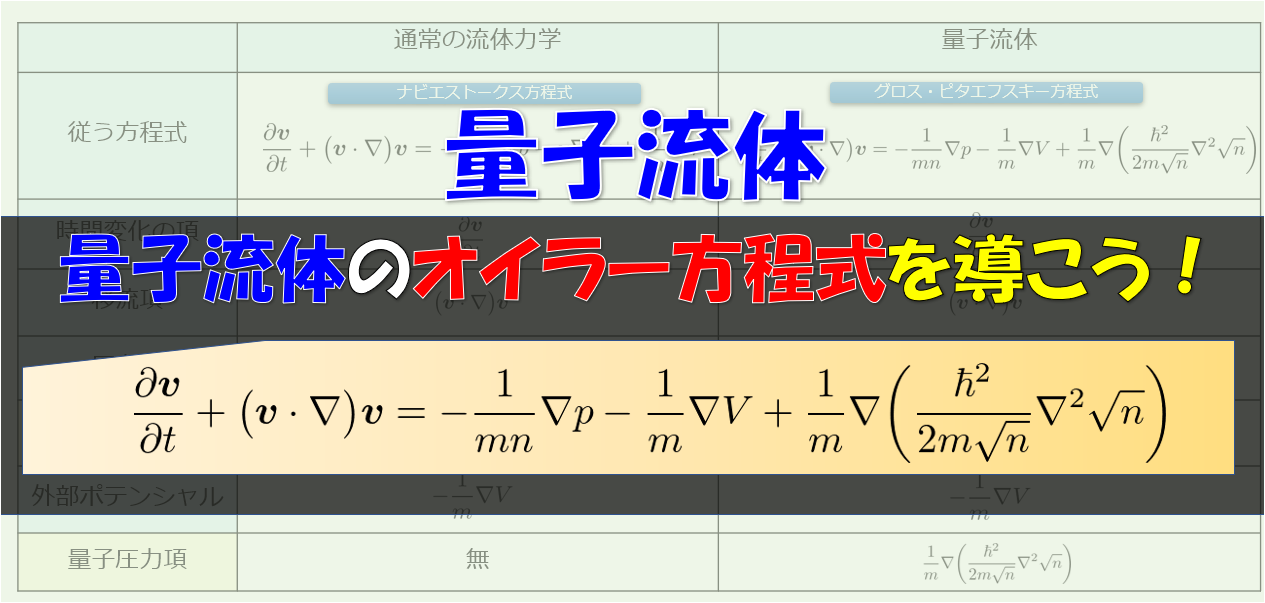
まず、量子渦の構造を考えるにあたって、量子流体が従う方程式を復習しておきます。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi(\boldsymbol{r})+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{1}
\end{align*}
量子流体は低温状態における大多数のボース粒子が最低エネルギー状態に落ち込んだときに起こるボースアインシュタイン凝縮ですが、従う方程式はとてもシンプルでシュレディンガー方程式に非線形項(右辺第3項)が加わっただけでした。
そして、状態については凝縮体の波動関数(秩序変数)を\(\psi=\sqrt{n}e^{i\theta}\)とおくことで定義付けられます。
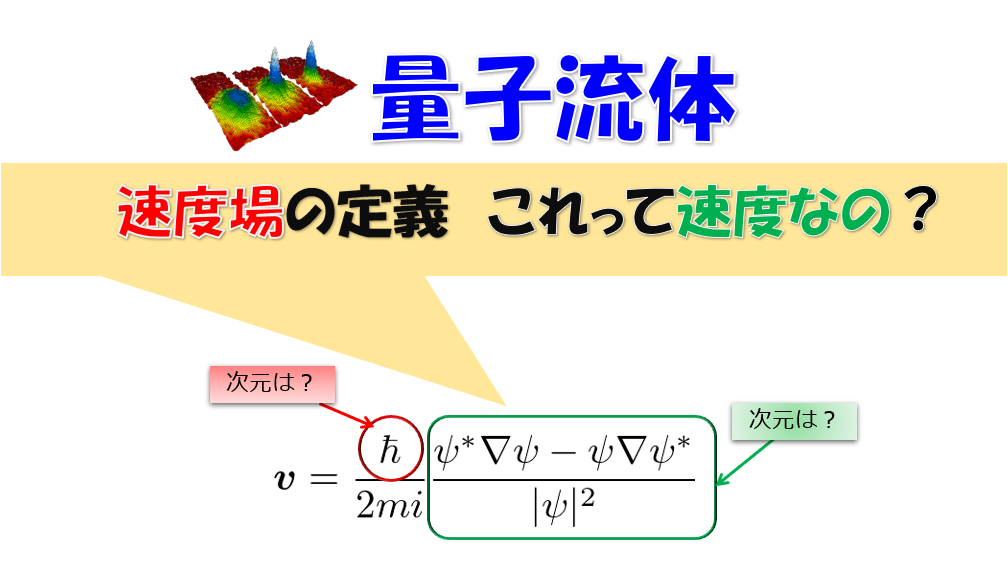
この波動関数を用いて速度場を、
速度場
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{2}
\end{align*}
と定義していました(‘◇’)ゞ
ここまでが復習です!!
ここから1本の量子渦について考えていきます。
1本の量子渦
1本の量子渦での波動関数がどのように書くと都合が良さそうかというのを考えていきます。
捕獲ポテンシャルが軸対称なのだから凝縮体の密度も軸対称の形にすれば良い。
下記のように、捕獲ポテンシャル\(V_{ext}=\frac{1}{2}m(x^2+y^2)\)(調和振動子ポテンシャル)で凝縮体が捕獲されているとします。
※\(z\)軸方向には凝縮体は一様として、ものごとを2次元で考えています。
そこに中央に1本の量子渦が「うにょっ」っと生成されているような状況を考えることにしましょう(^^)/
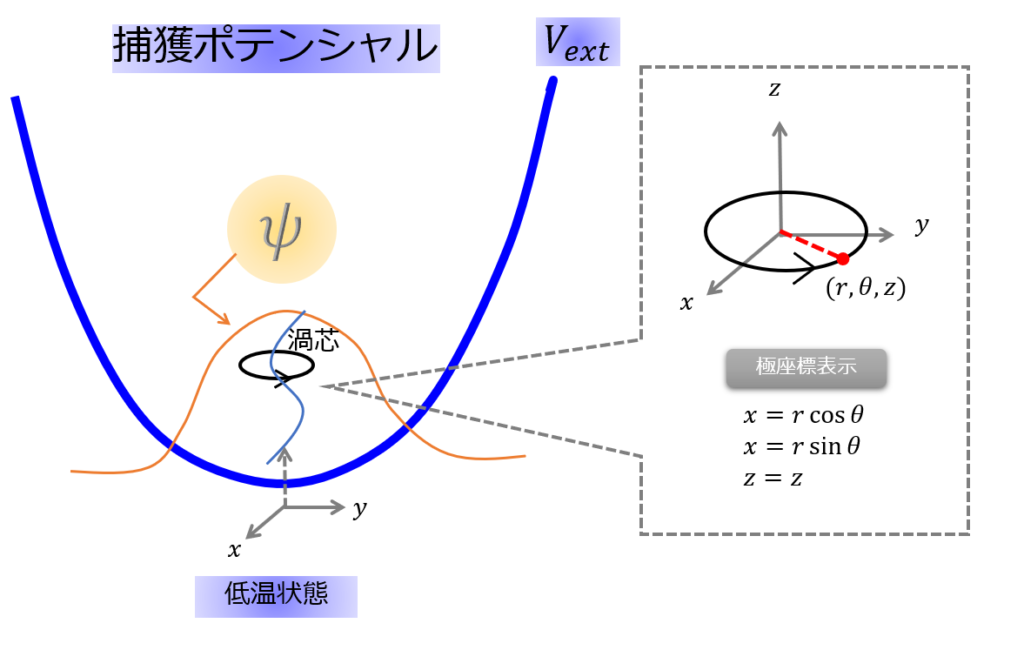

こういう状況においては、捕獲ポテンシャル\(V_{ext}=\frac{1}{2}m(x^2+y^2)=\frac{1}{2}mr^2\)のように軸対称の表式で書くことができます。
そうすると、凝縮体の密度\(n(\boldsymbol{r})\)も軸対称の解であるということになります。
\psi(\boldsymbol{r})=\sqrt{n(\boldsymbol{r},t)}e^{i\theta(\boldsymbol{r},t)}\tag{3}
\end{align*}
ここで思い出しておきたいことがあります(^^)/
1本の量子渦を考えていますが、量子渦の古典渦との違いは・・・・
量子渦の循環は\(\kappa=\frac{h}{m}\)に量子化されていたということです。
\Gamma_{c}=\oint_{c} \boldsymbol{v}\cdot d\boldsymbol{r}=\frac{\hbar}{m}\oint_{c}\nabla\theta d\boldsymbol{r}=\frac{\hbar}{m}2\pi l=\frac{h}{m}n\tag{4}
\end{align*}
\(l=0,\pm 1,\pm 2,\cdot\cdot\cdot\)
この\(l\)を使い、位相\(\theta\)の範囲を[\(0,2\pi\)]と制限すると波動関数を下記のように書いておくことができます。
\psi=\sqrt{n(r,z,t)}e^{i\theta}\tag{5}
\end{align*}
ちょっとこの後の微分の取り扱いをしやすくするために、\(\sqrt{n(r,z,t)}=f(r,z,t)\)と置くことにします。
\psi=f(r,z,t)e^{i\theta}\tag{6}
\end{align*}
これで極座標の表示、量子渦の循環の量子化を使った波動関数の表式が完了です。
時間に依存しない非線形シュレディンガー方程式
今回考えている1本の量子渦は、時間に依存せず安定に存在し続けることができますので(1)式の定常解となります。
量子力学でのシュレディンガー方程式では、波動関数が時間に依存しない場合は、\(\psi(\boldsymbol{r},t)=g(\boldsymbol{r})h(t)\)と時間と空間を分離することで、\(\psi(\boldsymbol{r},t)=g(\boldsymbol{r})e^{-i\frac{E}{\hbar}t}\)と書けることがわかっています。
※今の場合の空間座標は(\(r,\theta,z\))です。
今回であれば、\(g(\boldsymbol{r})=f(r,z)e^{i\theta}\)に対応しています。
だから、\(\psi=f(r,z)e^{i\theta}\)に時間変化分\(e^{-i\frac{E}{\hbar}}t\)を掛けることで波動関数の定常解の表式になります。
定常解を\(\psi=f(r,z)e^{i\theta}e^{-i\frac{E}{\hbar}}t\)と書いて(1)式に代入します。
そうすると(1)式の左辺だけが変わって・・・
E\psi(\boldsymbol{r})=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi(\boldsymbol{r})+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{7}
\end{align*}
(1)式に、\(\psi=f(r,z)e^{i\theta}e^{-i\frac{E}{\hbar}t}\)を考慮すると(7)式になったので、もはや\(e^{-i\frac{E}{\hbar}}t\)の掛け算を書く必要もないので波動関数を(6)式\(\psi=f(r,z)e^{i\theta}\)として、(7)式について考えれば良いということになります。
グロス・ピタエフスキー方程式の極座標表示
座標系を極座標表示に直してグロス・ピタエフスキー方程式を考える方が都合が良さそうなので、グロス・ピタエフスキー方程式の極座標表示を記述したいと思います。
ここは結論だけ書いておきたいと思います。
局所座標系でのグロス・ピタエフスキー方程式(略してGP方程式)
-\frac{\hbar^2}{2m}\bigg(\frac{1}{r}\frac{\partial}{\partial r}\bigg(r\frac{\partial \psi(\boldsymbol{r})}{\partial r}\bigg)+\frac{1}{r^2}\frac{\partial^2\psi(\boldsymbol{r})}{\partial \theta^2}+\frac{\partial^2\psi(\boldsymbol{r})}{\partial z^2}\bigg)+V_{ex}(r,z)\psi(\boldsymbol{r})+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})=E\psi(\boldsymbol{r})\tag{8}
\end{align*}
一番面倒な局所座標系でのラプラシアン\(\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}=\frac{1}{r}\frac{\partial}{\partial r}\big(r\frac{\partial}{\partial r}\big)+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}+\frac{\partial^2}{\partial z^2}\)の導出はここをご参考ください。
デカルト座標での偏微分を極座標での偏微分に変える手続きは・・・・めっちゃめんどうです。
では、\(\psi=f(r,z)e^{i\theta}\)を(8)式に代入してみましょう。
-\frac{\hbar^2}{2m}\bigg(\frac{1}{r}\frac{\partial }{\partial r}\bigg(r\frac{\partial f}{\partial r}\bigg)+\frac{\partial^2 f}{\partial z^2}\bigg)+\frac{\hbar^2l^2}{2mr^2}f+V_{ex}(r,z)f+gf^3=Ef \tag{8}
\end{align*}
※全ての項に\(e^{ij\theta}\)が出てくるので、割って消去しました。
まとめ
1本の量子渦が軸対称であるため、グロス・ピタエフスキー方程式を極座標表示で書きなおしました(‘◇’)ゞ
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi(\boldsymbol{r})+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{1}
\end{align*}
※↑デカルト座標での表記
↓極座標表示で書くと・・・※定常解\(\psi(r,z)=f(r,z)e^{il\theta}\)
-\frac{\hbar^2}{2m}\bigg(\frac{1}{r}\frac{\partial }{\partial r}\bigg(r\frac{\partial f}{\partial r}\bigg)+\frac{\partial^2 f}{\partial z^2}\bigg)+\frac{\hbar^2l^2}{2mr^2}f+V_{ex}(r,z)f+gf^3=Ef \tag{8}
\end{align*}