どうも、こんちには(@t_kun_kamakiri)(^^)/
流体力学の現象の中でも最も主役になりやすい渦・・・・
その中でも量子力学的効果によって現れる量子渦との違いについて紹介します。
- 日常よく見かける通常の流体を古典流体（左）
- 絶対零度（付近）での量子力学的効果による流体を量子流体（右）
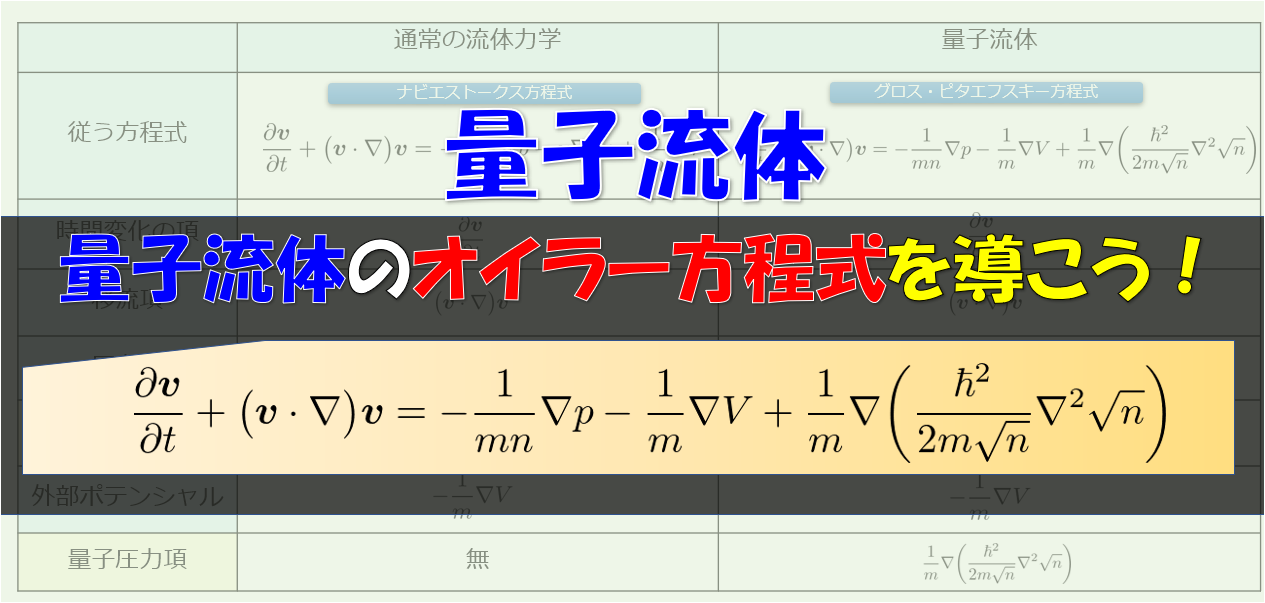
と呼び、両者は現象を記述するための方程式はめちゃくちゃよく似ています（↓こんな感じ）。
異なるのは、量子流体には粘性項が無く代わりに量子圧力項と呼ばれるものがあります。
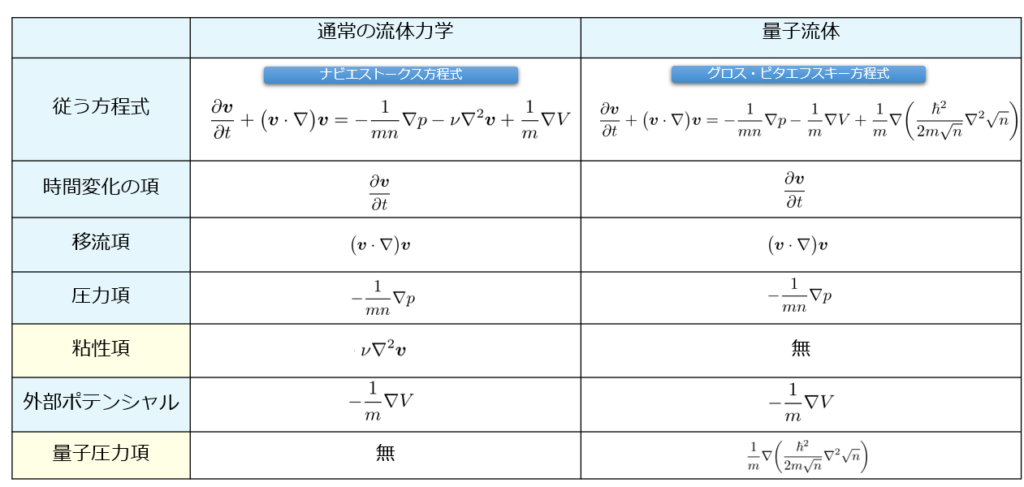
このように古典流体と量子流体は似ているところがあれば、異なるところもあるのです。
では、渦についての違いはあるのでしょうか？
それぞれの渦の呼び名を以下のように定めることにします。
- 古典流体の渦を古典渦
- 量子流体の渦を量子渦
この記事を読んで、「なんかわかったような気がする！！」と思ってもらえればOKです。
古典渦と量子渦の違いを見るための4つの着眼点
古典渦と量子渦の違いをみるにあたって何の違いを見るかを決めておく方が、よりはっきりと違いを認識して記憶することができるでしょう。
以下の違いを見ていきます。
- 循環（速度場の1周線積分）・渦芯
- 速度場
- 安定に存在しうるかどうか
この3つの着眼点に従って違いを見ていくことにします。
古典流体の渦（古典渦）
まずは、古典渦から見てきましょう(^^)/
古典渦はどのような渦か？
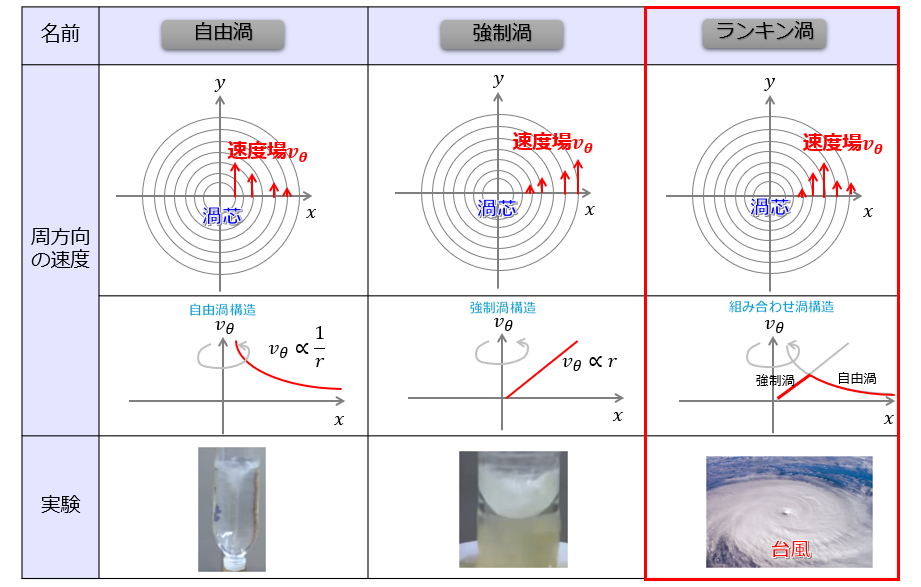
基本的には3つの渦があるので簡単に図でまとめておきました。
- 自由渦
- 強制渦
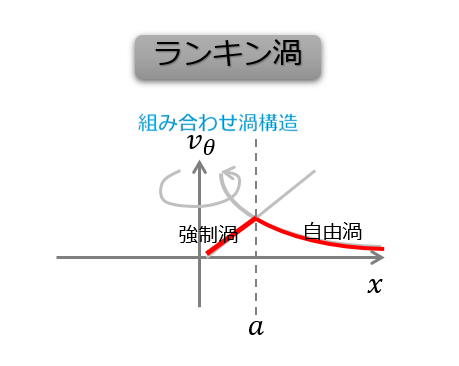
- ランキン渦
そしてそれぞれの渦の流速の分布が異なるということです。
しかし、完全な自由渦は自然界には存在しないようです。
自然界で多くみられるのは、ランキン渦（渦芯付近が強制渦、外側が自由渦）の方みたいです。
ですので古典渦を基本的には代表してランキン渦のみにして、量子渦と比較したいと思います。
ランキン渦の3つの仮定
- 流体は完全流体である。
- 流速は高さz 方向の成分を持たず、またz に依存しない。すなわち2次元流れである。
- 外力（ここでは重力）はポテンシャルを持つ保存力である。
※しかし、基本的な古典渦の特徴を語る上ではこだわりすぎることもないでしょう。
古典渦の循環は？
流れ場があるところに、閉曲線\(C\)を適当に描くことにします。
その閉曲線に沿って、流速の速度場で一周線積分します。
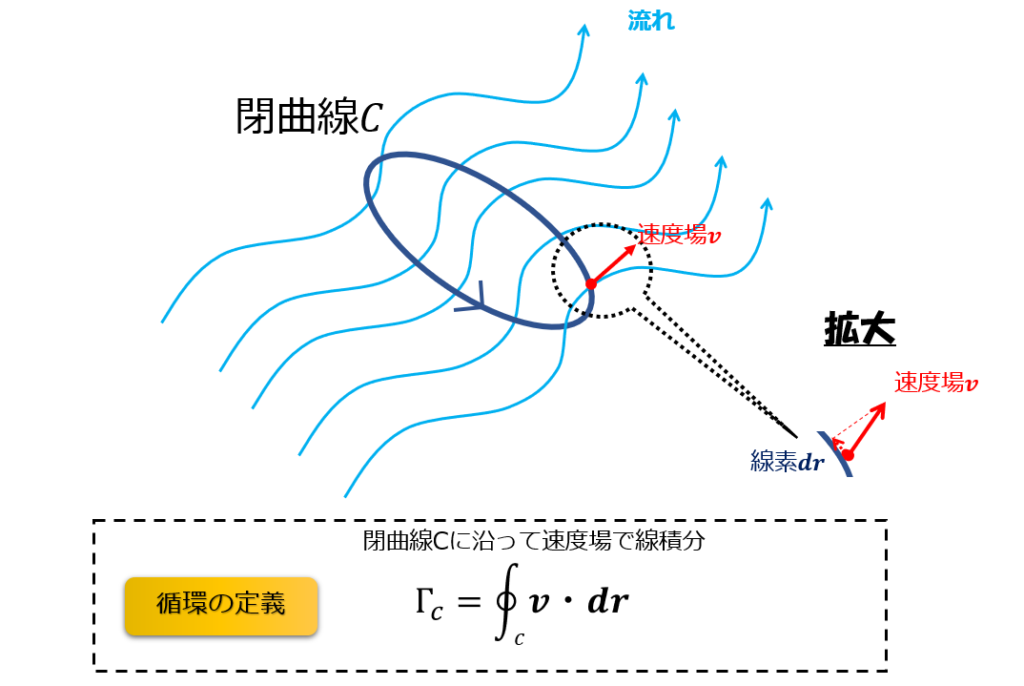
このように、流れがあるところに閉曲線\(C\)を適当に作り、流速の速度場で一周線積分したものを循環と言います。
↑上の記事でも詳しく書いていますが、循環の意味をもう少し説明しておきます。
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{v} \bigg)\cdot\boldsymbol{n}dS\tag{3}
\end{align*}
とこうなります。
ここで、\(\nabla\times\boldsymbol{v}=\boldsymbol{\omega}\)が渦度\(\boldsymbol{\omega}\)の定義なので、
循環は渦度を使って、
\Gamma_{c}=\iint_{S}\boldsymbol{\omega}\cdot\boldsymbol{n}dS\tag{4}
\end{align*}
となります。
これをマンガちっくに書くと・・・
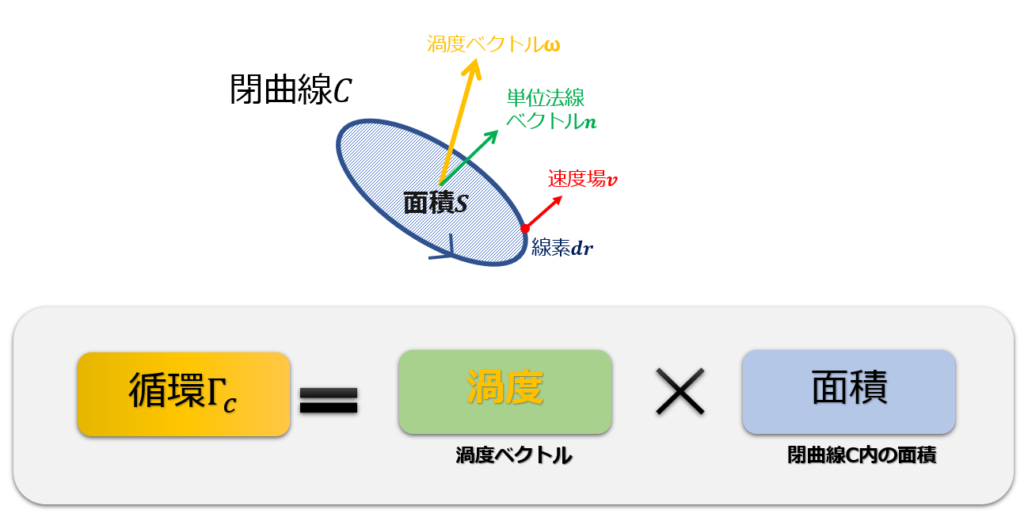
こんな感じです。
循環は、「渦度」と「閉曲線で囲まれた面積」との掛け算ということになります。
ここで、古典流体の場合は特に渦度に制限もなければ、渦芯の太さにも制限がありません。
ということは、渦芯の太さは何でも良いし、渦度も連続的だし・・・
つまり、「渦芯の太さも渦度も連続的（なんでも良い）」ということは、「渦芯はあいまい」であるという言い方ができます。
どこからどこまでが渦芯と言って良いのかわからないということです・・・
古典渦の速度場は？
上でランキン渦について説明しましたが、速度場を見ると渦芯で0、外側に行くに従って増加し、ある半径\(a\)でまた減衰していきます。
v_{\theta}(r)=\left\{\begin{matrix}
\frac{\omega}{2}r (r<a) \\ \frac{\omega a^2}{2r}(r>a)
\end{matrix}\right.\tag{1}
\end{align*}
↑この式の導出には3つの仮定をお忘れなく。
ランキン渦の3つの仮定
- 流体は完全流体である。
- 流速は高さz 方向の成分を持たず、またz に依存しない。すなわち2次元流れである。
- 外力（ここでは重力）はポテンシャルを持つ保存力である。
詳しくはこちらの参考書で勉強しましょう(^^)/
【補足説明】
渦をもっと単純に考えて半径\(a\)の内側は、渦度\(\omega=const\)として、外側は渦度\(\omega=0\)とシンプルにします。
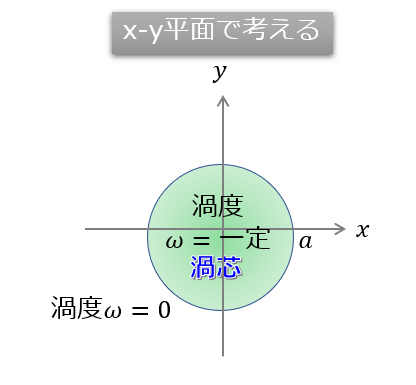
このような単純な場合は、(1)式を循環\(\Gamma_{c}=\oint_{c} \boldsymbol{v}\cdot d\boldsymbol{r}=\iint\omega dS=\omega \pi a^2\)を使うと、
v_{\theta}(r)=\left\{\begin{matrix}
\frac{\Gamma_{c}}{2\pi a^2}r (r<a) \\ \frac{\Gamma_{c}}{2\pi r}(r>a)
\end{matrix}\right.\tag{2}
\end{align*}
古典渦の安定性はどうか
古典渦の場合は、渦は「生成・消滅」を繰り返します。
- なぜ、渦を生成・消滅するのか？
- なぜ、渦の拡散が起こっているのか？
- なぜ、渦を生成・消滅するのか？
⇒渦が生成・証明をする根本の原因は「流体における粘性」です。
※古典流体の場合は、粘性項があることでケルビンの循環定理を破ります。
流体力学 ケルビンの循環定理【渦ができる要因を理解する】
- なぜ、渦の拡散が起こっているのか？
また、拡散する原因も「流体における粘性」です。
>>拡散方程式(wikipedia)
つまり、古典流体は粘性によって生成消滅・拡散が起こるということです。
量子流体の渦(量子渦）
では、つぎに量子渦について見ていきましょう(^^)/
量子渦の循環は？循環は量子化される
量子渦と古典渦の最も大きな違いというのは、この循環についてです。
古典渦の場合は循環は連続的で任意の値をとることができましたが、量子渦の場合は？・・・・
循環が量子化されていて、とびとびの値しかとることができません(/・ω・)/
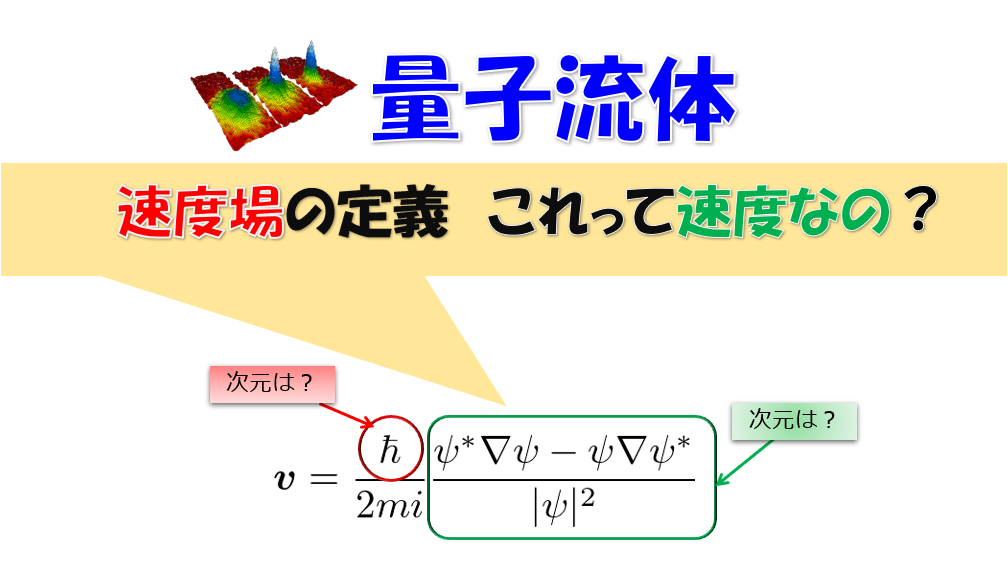
量子渦の循環・・・の前に、量子流体での速度場の定義を復習しておきます。
凝縮体の波動関数(秩序変数）を\(\psi=\sqrt{n}e^{i\theta}\)とおき、速度場を、
速度場
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{5}
\end{align*}
と定義していました(‘◇’)ゞ
では、循環を計算します。
波動関数\(\psi=\sqrt{n}e^{i\theta}\)は1価関数なので、下記の線積分しても波動関数は同じにならないといけません。
※位相差\(\nabla\theta\)は\(2\pi\)の整数倍にならないといけない
\Gamma_{c}=\oint_{c} \boldsymbol{v}\cdot d\boldsymbol{r}=\frac{\hbar}{m}\oint_{c}\nabla\theta d\boldsymbol{r}=\frac{\hbar}{m}2\pi l=\frac{h}{m}n\tag{6}
\end{align*}
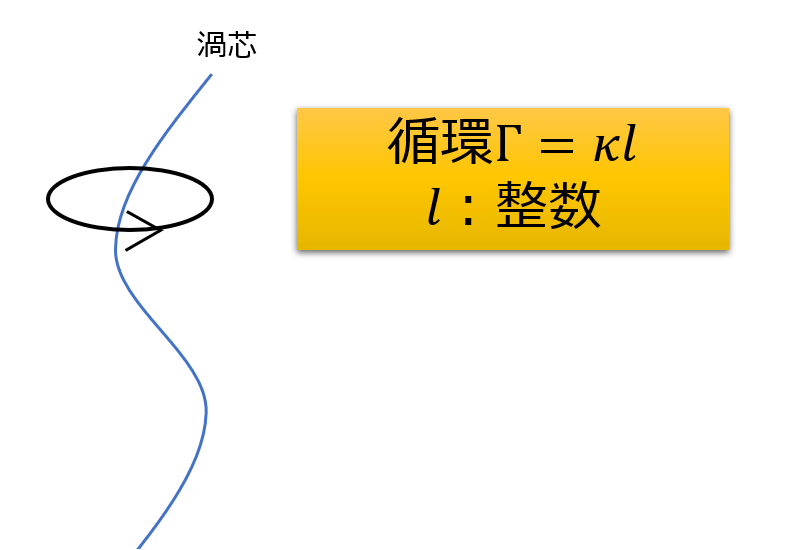
\(l=0,\pm 1,\pm 2,\cdot\cdot\cdot\)
このように量子渦の循環は、循環量子\(\kappa=\frac{h}{m}\)を単位として、量子化されています。
量子渦の速度場は？
1本の量子渦の速度場は、古典渦と違って自由渦のような速度場になります。
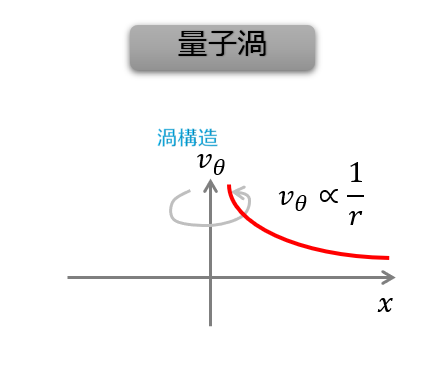
\frac{\Gamma_{c}}{2\pi r}\tag{7}
\end{align*}
ん？
これだと運動エネルギーが渦芯で発散しないのか？・・・というのが気になるところですが、量子渦の渦芯構造の密度は0です。
密度を0にすることで、エネルギーの増加を回避しています。
古典渦の場合は「1本の渦」と言わずに、量子渦の場合だけ「1本の量子渦」と書いたのには理由があります。
古典渦の場合は循環が任意の値をとれるし、渦芯もあいまいでしたので、これが1本の渦と断定するのには情報があいましすぎるのですよね(‘ω’)
ですが、量子渦の場合は循環量子\(\kappa\)で量子化されているので、1本の渦の定義が明確です。
| 超流動ヘリウム | \(10^{-10}m\)程度 |
| 希薄原子気体ボース・アインシュタイ凝縮体 | \(10^{-7}mm\)程度 |
いずれにしても、考えている全系の大きさに比べて非常に細いです。
ゆえに、量子渦は1本の渦の定義と渦芯が明確であると言えます。
※詳しくは触れませんが、\(n\neq 2\)の渦の生成は\(n=1\)の渦の生成と比べてエネルギー的に不安定となるため、\(n=1\)の量子渦のみが存在します。
量子渦の安定性はどうか
量子流体自体には、粘性項もなければ拡散項もありません（絶対零度では・・）。
ゆえに1本の量子渦が存在していた場合に、それを消滅させたり拡散させたりする機構がありません(‘ω’)
ということは、量子渦は安定に存在するのです(^^)/
※量子渦と量子渦が接近する場合は、渦同士で繋ぎ変えを起こしたりします。
※有限温度の場合は、音波として渦そのものが消滅します。
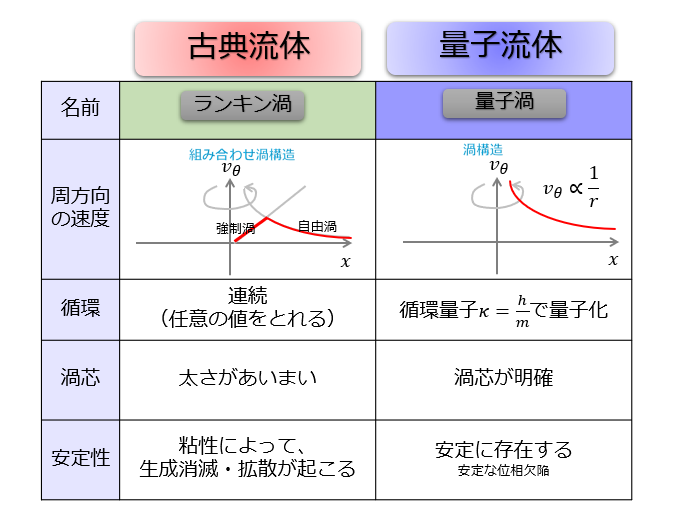
まとめ
本記事では、古典流体での渦(古典渦）と量子流体での渦（量子渦）についての違いを解説してみました(‘◇’)ゞ
まとめると、以下の表になります。
まだ、理解していない点が多いですが、引き続き勉強を続けます(^^)/
Follow @t_kun_kamakiri
