こんにちは(@t_kun_kamakiri)
自宅でCAE解析をしたいと思ったことはありませんかね?
そんな人には・・・・無償で使用できるCAE解析ソフトElmerがおすすめです♪
このCAE解析ソフトElmerを用いて、自宅で無料でCAE解析を行いたいと思います。
※こちらの記事を読んでいることが大前提です(^^)/
CAE解析の中でも、本記事は流体解析について紹介したいと思います。
- 流体解析の理論を少し復習したい人
- 趣味で流体解析を自宅でしたい人
- Elmerを使ってみたいけど使い方がわからない人
※大学2回生までに習う偏微分、ベクトル解析を勉強している方を対象にしています。
どんな数学を学べば良いかはこちらの記事を参考にしてください。
本記事では、Elmerのドキュメントを参考に以下の2つを解説します。
- 流体力学の理論の解説
- Elmerを使ったカルマン渦列の生成(動画)
※音声無しです(‘ω’)
前半は理論の解説です。
後半がElmerを使った流体解析についてです。
理論をしっかり学びたい人は、前半も読んでやってください。
理論なんて読んでいるとイライラする人や、そんな理論は常識だっていう人は一気に「動画でElmerのGUIの解説」まで章を飛ばしてください。
本記事のElmerを使った解析結果はこんな感じです↓
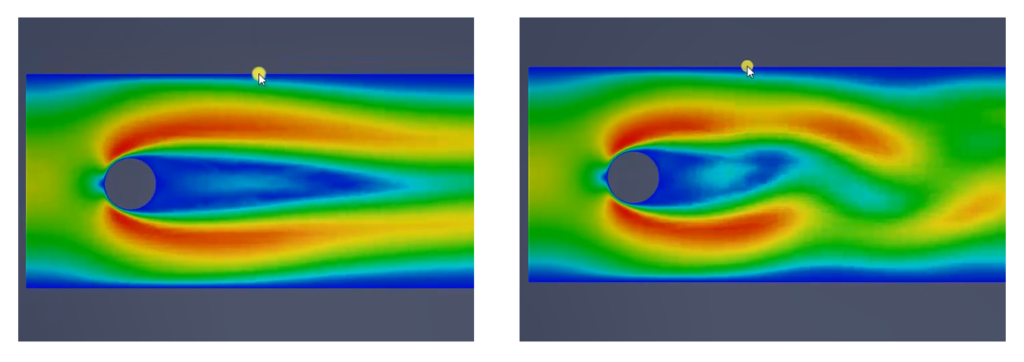
※PCの環境
- Windows10
- Intel Core i7@2.50GHz 2.6GHz
- メモリ8G
※Elmerのversion
- Elmer 8.3
流体力学の理論解説
Elmerのホームページから理論解説のドキュメントを入手
Elmerに関するドキュメントはホームページのこちらから入手することができます。
↓ホームページ
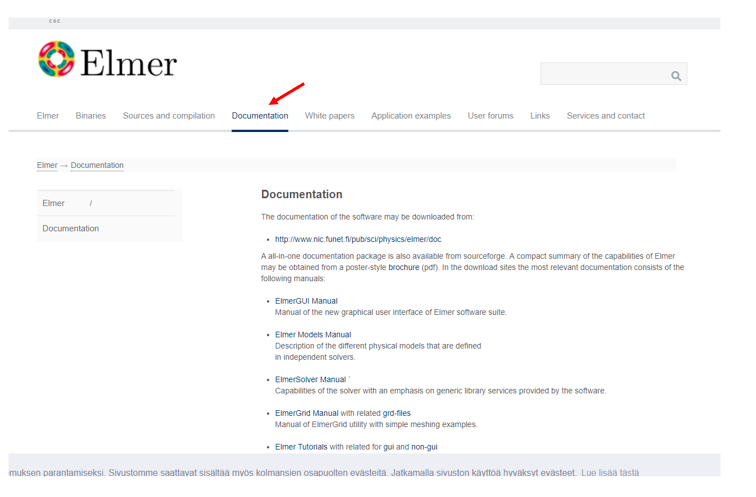
理論解説は、以下のドキュメントを参考にしています。
http://www.nic.funet.fi/pub/sci/physics/elmer/doc/ElmerModelsManual.pdf
しかし、英語である上に流体力学の基礎方程式は少々ややこしいので、まずはこのドキュメントの補足説明を簡単にしたいと思います。
基本的に流体力学で解くべき方程式は4つ
下記の(1)~(3)式はある物理量の輸送方程式の一般系から導くことができます。
※密度変化が小さいとして、密度を定数として扱う場合の非圧縮性を仮定ならば基本的に解くべき方程式は2つになります。
↓「非圧縮性流体」の記事をは下記をご参考ください
Elmerのドキュメントの流体力学の理論解説
続いて、↓下記のドキュメントのP.20の解説を行います。
http://www.nic.funet.fi/pub/sci/physics/elmer/doc/ElmerModelsManual.pdf
※本記事の式番号はドキュメントの式番号です。
※本記事はドキュメントの直訳ではありません。
まず、流体力学の基礎方程式を以下に示します。
運動量保存則
質量保存則
※ここで\(\bar{\bar{\sigma}}\)、\(\bar{\bar{I}}\)はテンソルを表しています。
\(\bar{\bar{\sigma}}\)をテンソル表記にすると、\(\sigma_{ij}\)と書き、これはコーシー応力と呼ばれます。
これは、圧力と粘性抵抗という内力に値する応力を意味しています。
ドキュメントには書いていませんでしたが、圧縮性の流体として問題を解きたい場合などは、エネルギー保存則の(3)式も使うことがあります。
非圧縮性の場合は、密度一定として扱うので\(\rho=const\)ですが、そのような仮定を用いない場合は下記の理想気体の状態方程式を使います。
(2.6)、(2.7)は熱力学でよく見かける理想気体の仮定において導かれる定義式ですね。
※\(C_{p}\):定圧比熱
※\(C_{v}\):定積比熱
ここまでが流体力学の基礎方程式です。
上記(2.1)~(2.7)までの式でに関して以下の2点の補足説明をしておきます。
- 「ニュートン流体か非ニュートン流体」かも区別していませんし、「圧縮性か非圧縮性」かも区別していません。
- 理想気体の状態方程式以外の現象などは扱えません。
(例えばマッハ数が5以上の極音速領域などは理想気体の状態方程式では扱えない現象が存在しますのでご注意を。)
非圧縮性仮定の場合
ドキュメントには非圧縮性の方程式についての記述があったので、以下に示しておきます。
非圧縮性の仮定の場合は以下の2つを解きます。
運動量保存則
質量保存則
この2式を導出するには、まず非圧縮仮定\(\rho=const\)を用います。
すなわち、密度が時間にも空間にも依存しないとし、
\(\frac{\partial \rho}{\partial t}=0\)、\(\nabla\rho=0\)
となります。
そうすると、(2.2)式の左辺第一項の大括弧が丸ごと消えるので、(2.10)式が導けます。
この(2.10)式を(2.3)式に代入すると、
となるので、これを(2.1)式に代入すると(2.9)式になります。
運動量保存則(非圧縮性流体)
ここまでで理論についての解説が終わりです。
ブシネスク近似についての解説もドキュメントにありましたが、本記事とは直接関係ないため割愛します。
理論のまとめ
「流体力学の基礎方程式」と「密度一定にした場合の非圧縮性」で理論式をまとめておきます。
| 流体力学の基礎方程式 | 密度一定にした場合の非圧縮性 | |
| 運動量保存則 | \begin{align*}\rho\bigg(\frac{\partial \vec{u}}{\partial t}+(\vec{u}\cdot\nabla)\vec{u}\bigg)-\nabla\cdot\bar{\bar{\sigma}}=\rho\vec{f}\cdot\cdot\cdot (2.1)\end{align*} |
\begin{align*}\rho\bigg(\frac{\partial \vec{u}}{\partial t}+(\vec{u}\cdot\nabla)\vec{u}\bigg)-\nabla\cdot(2\mu\bar{\bar{\sigma}})+\nabla p=\rho\vec{f}\cdot\cdot\cdot (2.9)\end{align*} |
| 質量保存則 | \begin{align*}\bigg(\frac{\partial \rho}{\partial t}+(\vec{u}\cdot \nabla)\rho\bigg)+\rho(\nabla\cdot\vec{u})=0\cdot\cdot\cdot (2.2)\end{align*} |
\begin{align*}\nabla \cdot \vec{u}=0\cdot\cdot\cdot (2.10)\end{align*} |
| エネルギー保存則 | \begin{align*}\frac{\partial \rho E}{\partial t}+\frac{\partial \rho E v_{j}}{\partial x_{j}}=-\frac{\partial q_{j}}{\partial x_{j}}+\frac{\partial \sigma_{ij}v_{j}}{\partial x_{j}}+\rho K_{j}v_{j}\cdot\cdot\cdot (3)\end{align*} \(E=e+\frac{1}{2}\boldsymbol{v}^2\) e:内部エネルギー |
|
| 理想気体の状態方程式 | \begin{align*}\rho=\frac{p}{RT}\cdot\cdot\cdot (2.5)\end{align*} \begin{align*}R=\frac{\gamma-1}{\gamma}c_{p}\cdot\cdot\cdot (2.6)\end{align*} \begin{align*}\gamma=\frac{c_{p}}{c_{v}}\cdot\cdot\cdot (2.7)\end{align*} |
\begin{align*}\rho=const \end{align*} |
※流体力学の基礎方程式は「ニュートン流体」だけでなく「非ニュートン流体」も含みます。
Elmerのチュートリアル10:カルマン渦列の生成
ここからはElmerのチュートリアルを参考に、2次元の円柱回りの流れ(カルマン渦列の生成)をやっていきたいと思います。
↓下記のドキュメントのP.50を参考にしてください。
http://www.nic.funet.fi/pub/sci/physics/elmer/doc/ElmerTutorials.pdf
解析条件
流体領域
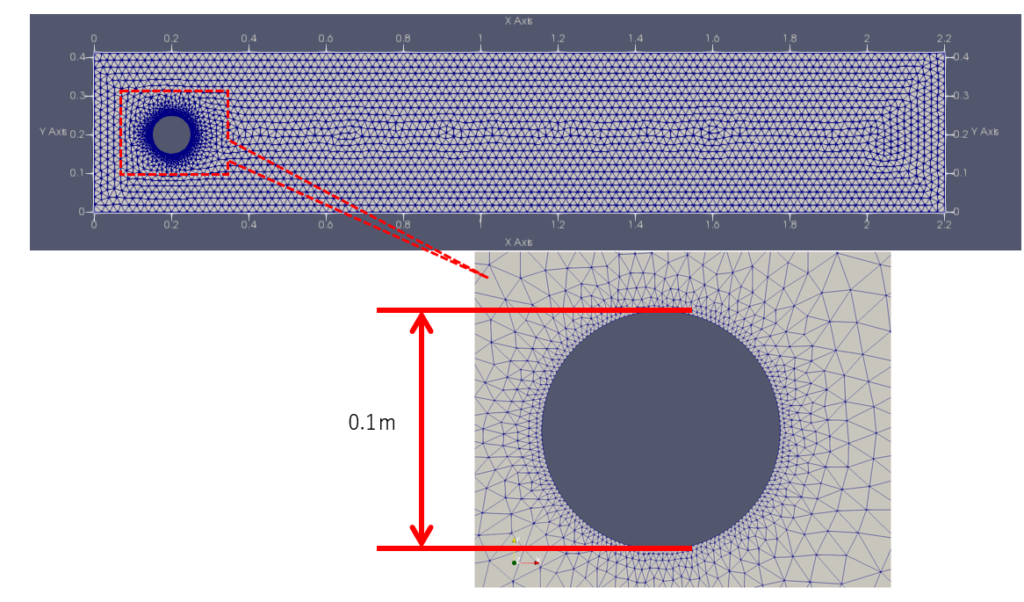
解くべき方程式
- 運動量保存則
- 質量保存則
その他の条件
- 乱流モデル無し
- 非定常解析
- 粘性係数:0.001[Pa⋅s]
- 密度:1.0[kg/m3)]
- 終了時刻:10[s]
- 2次元の解析
動画でElmerのGUIの解説
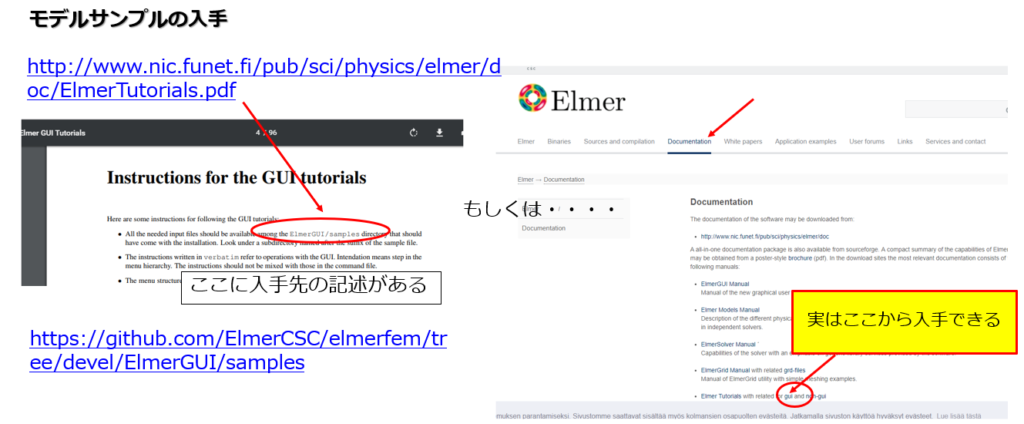
モデルのサンプルの入手先
チューリアルの解析モデルのサンプルは下記より入手することができます。
https://www.csc.fi/web/elmer/documentation
サンプルの入手先はどこかをドキュメント内で説明してありますがわかりにくかったです。(git内のある階層のフォルダを見てくれ的なことが書いてありました)
でも、「実はここから」入手できるんですよね。
操作方法の動画
これを見て皆さんもCAE解析を自宅でお楽しみください・・・・
まとめ
今回は、フリーのCAE解析ソフトElmerを使って流体解析を自宅のPCで行ってみました。
感想は、英語ですがドキュメントが豊富でチュートリアルも充実しているのでフリーソフトとは思えないほど簡単に流体解析を体験することができました。
メリット
- 理論解説とチュートリアルが充実しているので簡単にCAE解析が体験できる。
(サンプルモデル有) - 基本はGUIでの操作なので設定なので初心者のハードルを下げている。
- 無料でCAE解析ができる。
デメリット
- 日本語のドキュメントが少ない(ほとんどない)。
- GUIはあるが解析設定がフローのようになっていないので少しわかりづらい。
今後はこのような使いやすくて、無料でCAE解析ができるツールが増えていってほしいなと思います。