熱力学

気体の膨張で板が動くシナリオを熱力学第一法則と理想気体から考える

本記事の内容

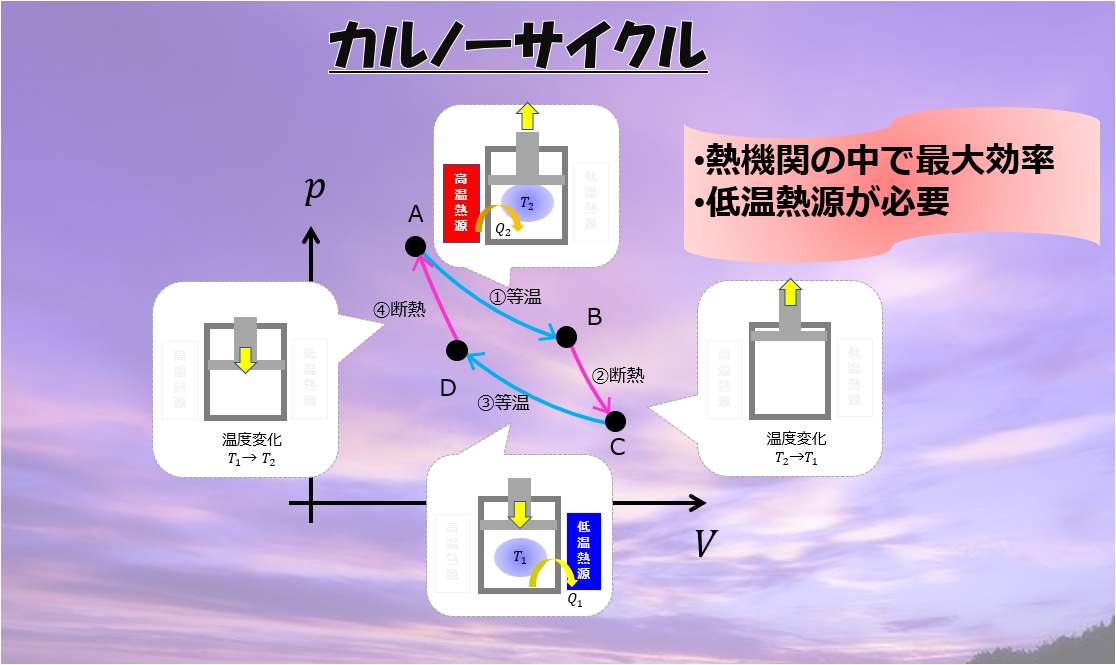
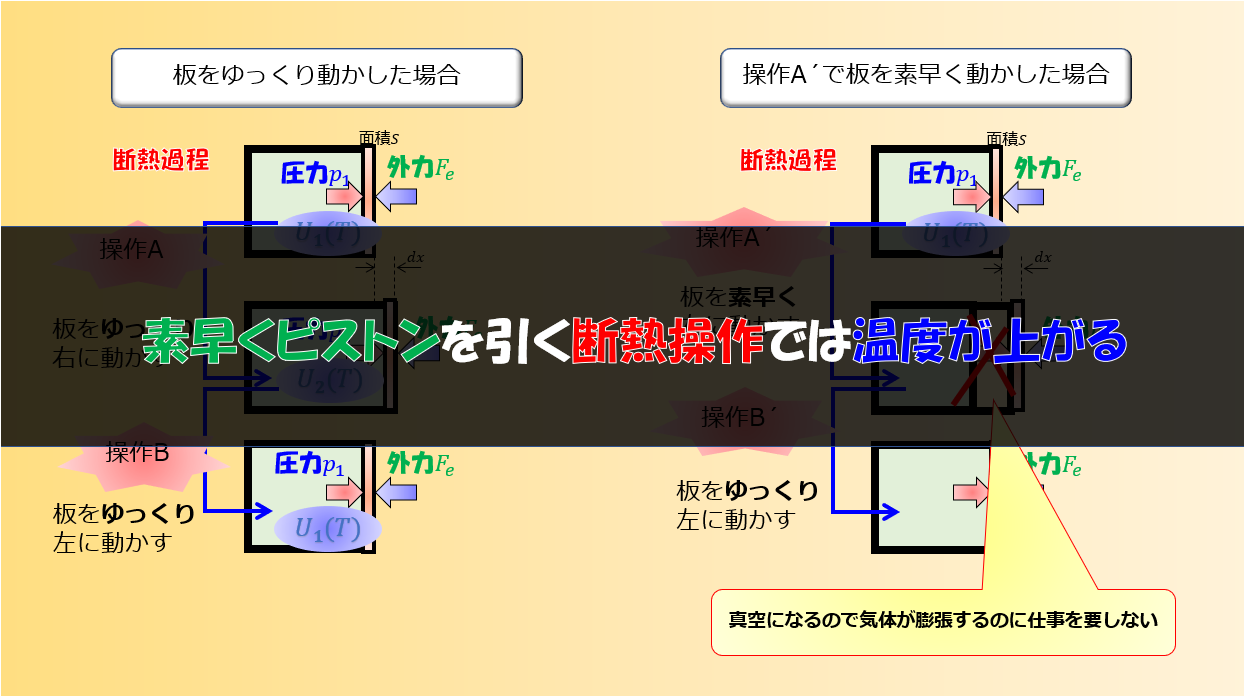
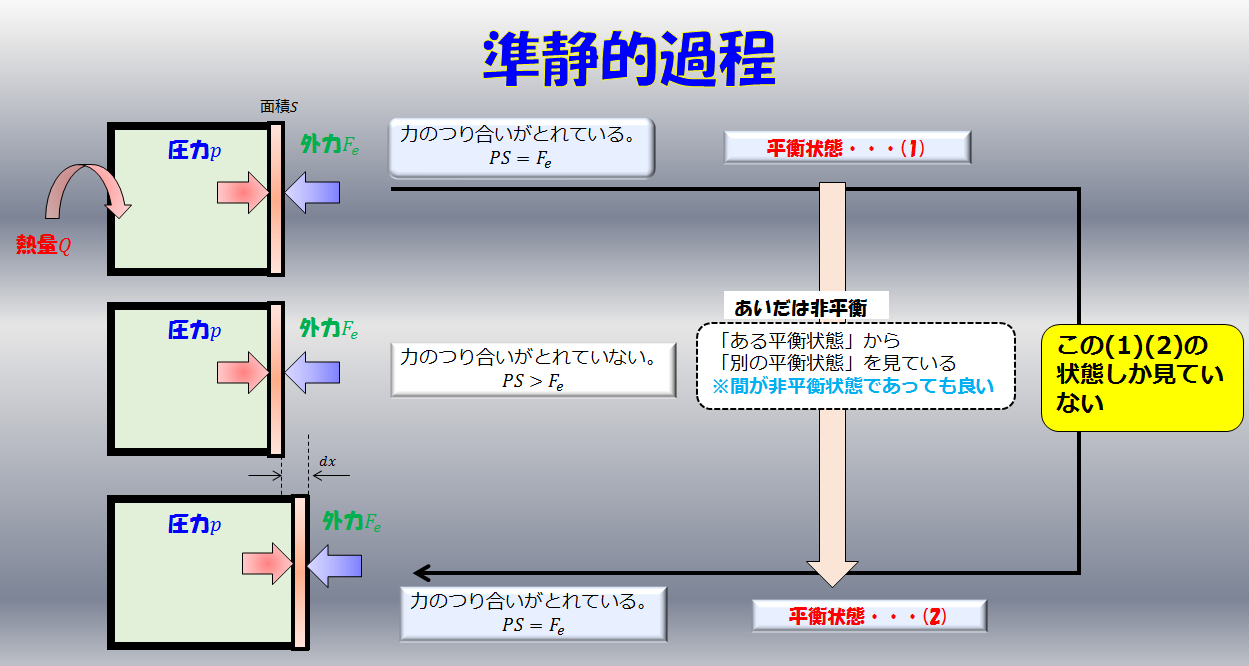
熱力学第一法則と理想気体の状態方程式を使って問題が解けるというのを解説します。

熱力学の第一法則

\begin{align*}d^{\prime}Q=dU+pdV\end{align*}

はご存知の方も多いでしょう。

しかし、こう思うのです・・・・・
「こんなの知っていてだから何なんだ」ってね。

そこで本記事では「熱力学の第一法則」と「理想気体の状態方程式」を連立されることで、内部状態\(p\),\(V\),\(T\)などが求まるっていうことを紹介したいと思います。

※ここでの議論は理想気体の状態方程式に基づいているということを常に意識しておきましょう。

※\(dQ=dU+pdV\)は教科書では「状態量」と「状態量でないもの」を区別するために「’（プライム）」をつけて区別する場合があります。

あわせて読みたい

「熱力学第一法則の2つの書き方」と「状態量と状態量でないもの」

スポンサーリンク

熱力学第一法則と理想気体を連立させるとは？

以下に示していきますが、結論は

結論

\begin{align*}d^{\prime}Q=dU+pdV\tag{1}\end{align*}

のように、(1)(2)を連立させると、ある平衡状態から別の平衡状態を記述する理論が構築できるのです。

\begin{align*}p=(\gamma-1)\frac{U}{V}\tag{2}
\end{align*}

理想気体の状態方程式を定積比熱を用いて表現してみる

理想気体の状態方程式\(pV=nRT\)を定積比熱\(C_{v}\)を用いて表現することを考えます。定積比熱は、$\big(\frac{\partial U}{\partial T}\big)_{V}=nC_{v}$のように書けるので、\(pV=nRT\)と内部エネルギー\(U\)の関係が分かりそうです。
まず比熱比というものを定義します。

比熱比：\(\gamma=\frac{C_{p}}{C_{v}}\)
ここで、マイヤーの関係式$C_{p}=C_{v}+R$を使います。

あわせて読みたい

マイヤーの関係式とは？理想気体の定圧比熱と定積比熱の関係式

\begin{align*}R=C_{v}\bigg(\frac{C_{p}}{C_{v}}-1\bigg)=C_{v}(\gamma -1)\tag{3}
\end{align*}

これを、理想気体の状態方程式\(pV=nRT\)に代入してみます。

\begin{align*}p=(\gamma-1)\frac{nC_{v}T}{V}\tag{4}
\end{align*}

さらに定積比熱の定義$C_{v}=\big(\frac{\partial U}{\partial T}\big)_{V}$を積分すると、

\begin{align*}U=\int nC_{v}dT\tag{5}
\end{align*}

となります。

ここで、比熱の温度依存性がないとした場合は、

\begin{align*}U=nC_{v}T\tag{6}
\end{align*}

となるため、(4)式に代入することで下記のように「圧力」と「内部エネルギー｝の関係式を得ることができました。

\begin{align*}p=(\gamma-1)\frac{U}{V}\tag{7}
\end{align*}

そうすると、理想気体の状態方程式は単純に「圧力」「温度」「体積（密度）」などの熱力学的変数による関係式、いわゆる内部状態を表現しているだけに過ぎませんでしたが、そこに熱力学第一法則というエネルギー保存則を加えることで、力学的な理論へと発展していくことができます。
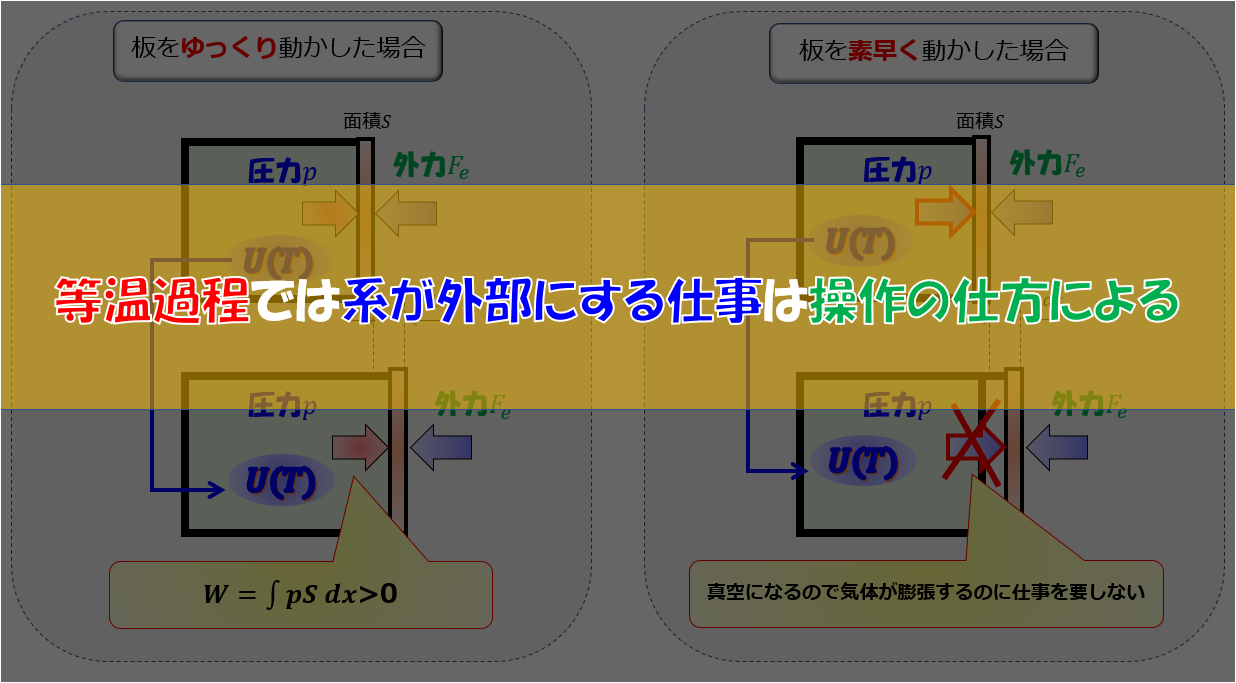
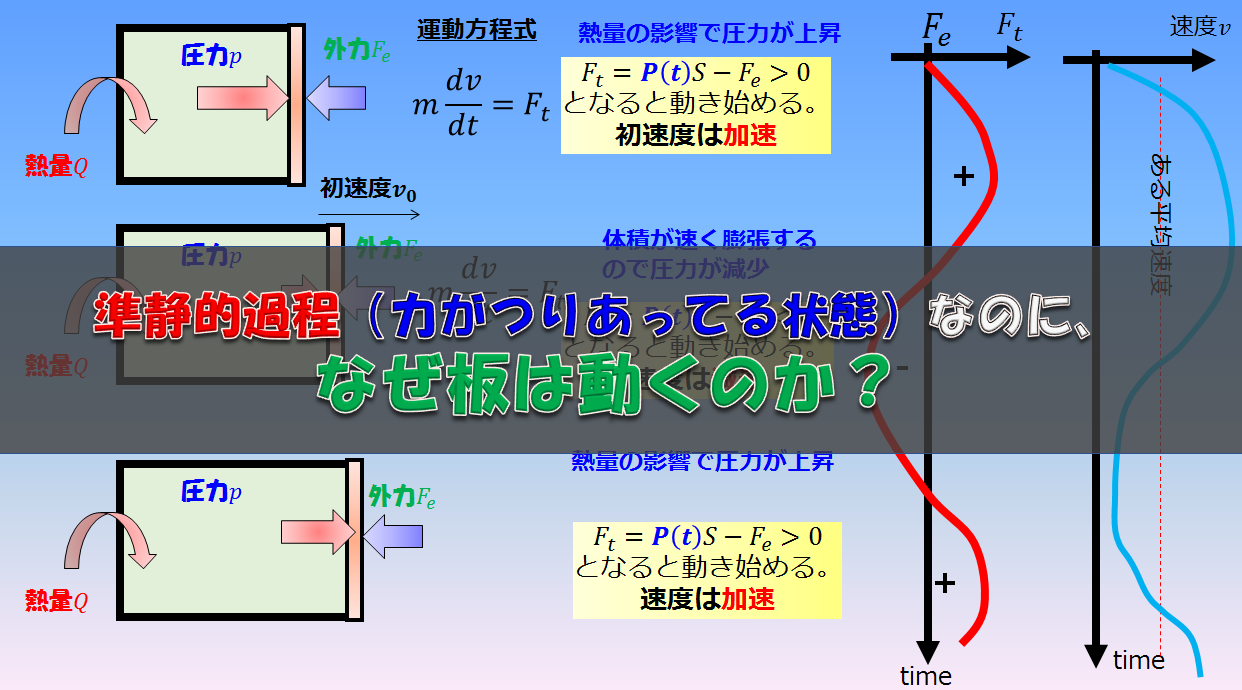
力学的な理論とは熱力学一法則\(d^{\prime}Q=dU+pdV\)の\(pdV\)の部分です。
熱力学的な圧力と力学的な圧力は（あまり深くは議論しないが）同じであることがわかっています。

要するに、

\begin{align*}d^{\prime}Q=dU+pdV\tag{1}
\end{align*}


\begin{align*}p=(\gamma-1)\frac{U}{V}\tag{2}
\end{align*}

このふたつを連立させると、ある平衡状態から別の平衡状態を記述する理論が構築できるのです。

関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です