こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事では熱力学で重要な物性値である、比熱についての解説をしたいと思います(^^)/
下記の記事は高校生でも読める内容にして比熱についてわかりやすく解説をしましたのでお読みください♪
また、本記事を読みこなすには熱力学第一法則についても知っておくと良いでしょう。
では、本記事の内容をまとめると・・・
- 定圧比熱と定積比熱の意味を理解しよう
- 定積比熱・定圧比熱の定式化を行おう
定積比熱・定圧比熱とは?
まずは定積比熱と定圧比熱の違いを簡単にまとめてみます。
定積比熱とは?
定積比熱とは、体積が変化しない状況下において定義されます。
たとえばどんな状況かというと、断熱容器に囲まれた系(何か物質:例えば鉄など)の1kgを、1℃上昇させるのに必要な熱量が定積比熱です。
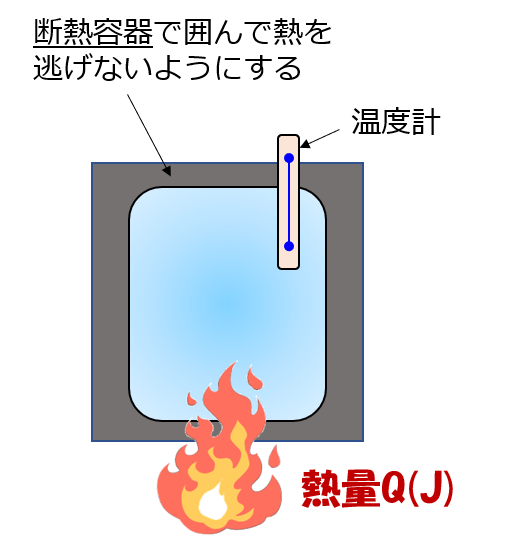
この場合は体積膨張しないので、加えられた熱量が全て内部に蓄えられるエネルギーになります。
定圧比熱とは?
定圧比熱とは、圧力が変化しない状況下において定義されます。
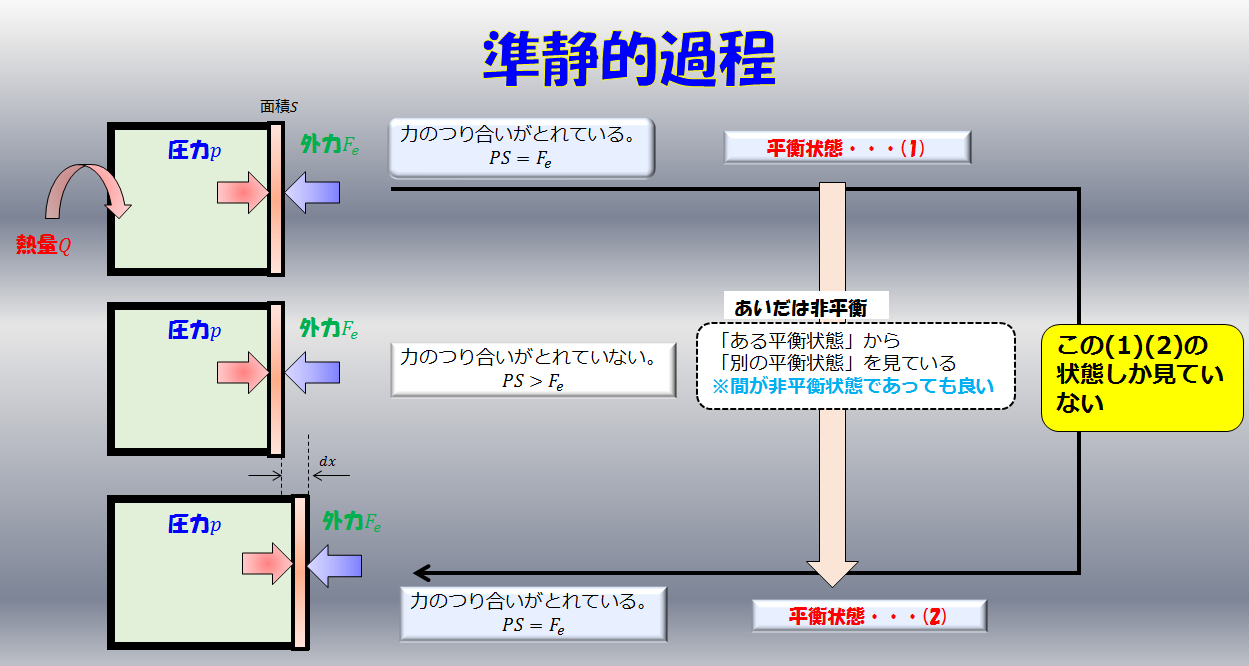
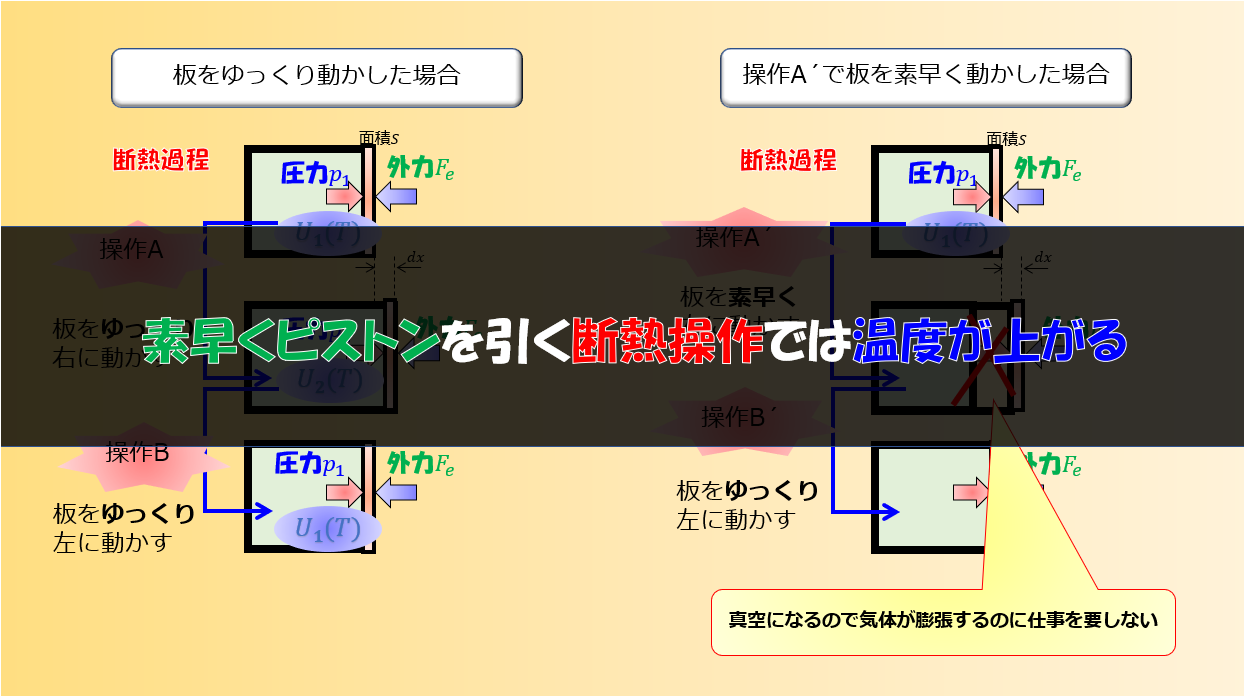
例えば、断熱容器に囲まれている容器の赤色の敷居は自由に動くものとすると、青色の系は常に大気圧と釣り合うくらいの力でゆ~っくり敷居を右へ押していきます(準静的過程)
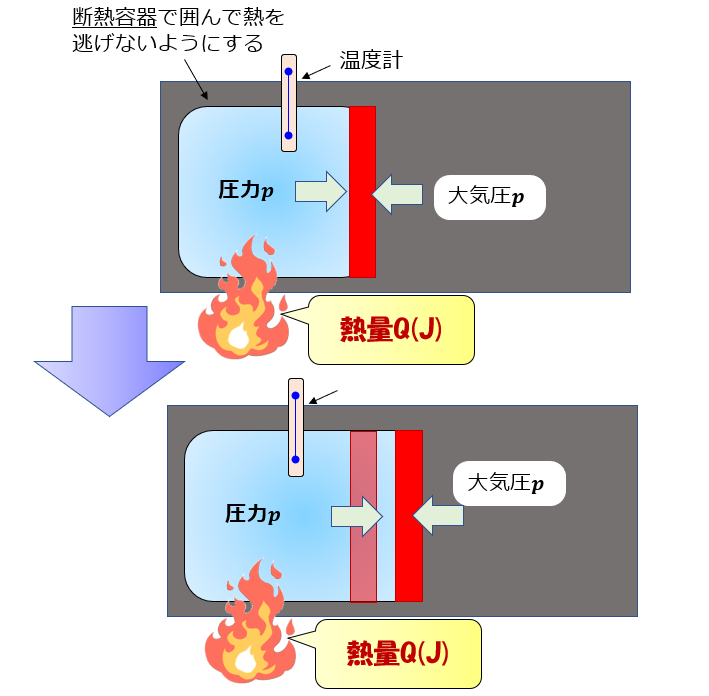
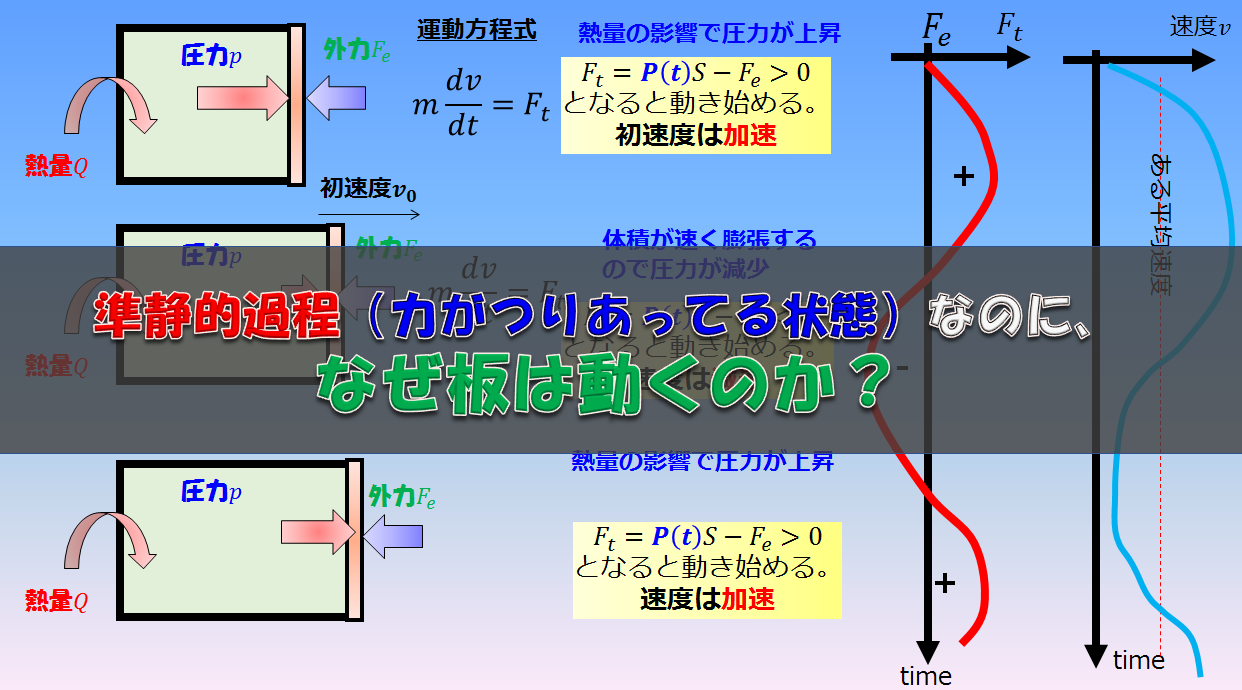
外気圧が大気圧$p$で準静的過程である場合は、力のつり合いから内部の圧力も$p$となります。しかし、力が釣り合っているのに「内部と外部を仕切っている板はなぜ動くのか?」ということが疑問に思いますよね。
それについて考察をしたのが以下の記事です。
結論、熱量が加えられて蓄えられた内部エネルギーで一瞬大気圧より圧力が増し(\(\alpha\))、圧力が増した分で外へ仕事をし体積膨張します(\(\beta\))。
しかし、体積膨張したのでまたもとの大気圧に戻ります。
※この(\(\alpha\))と(\(\beta\))の仮定がほぼ無視できるくらいの時間スケールである場合において平衡状態の熱力学というのはとても有効的です。
これを繰り返して、じわじわと膨張するような圧力が一定の状況下において単位質量当たり、1K(もしくは1℃)上昇させるのに必要な熱量(J)が定圧比熱になります。
熱力学第一法則を式変形
定圧比熱、定積比熱の定式化が本記事のお題であるので、まずは「熱力学第一法則」を下記に記します。
※外部へする仕事量は\(d^{\prime}W\)、気体の圧力\(p\)がする仕事のみを考えて\(d^{\prime}W=pdV\)と書きます。
※\(d^{\prime}Q=dU+d^{\prime}W\)は教科書では「状態量」と「状態量でないもの」を区別するために「’(プライム)」をつけて区別する場合があります。
「’(プライム)を付けたものは」状態量ではないということを明記することがあります。
これを式変形して定圧比熱、定積比熱の定式化を行います。
次の3つの環境下で考えることにします。
| No. | 環境下 | 0の変化量 |
| A | 圧力も体積も変化 | – |
| B | 体積一定 | \(dv=0\) |
| C | 圧力一定 | \(dp=0\) |
まず、一般(A)を述べた後で、具体的な(B)(C)と説明することにします。
一般論(A)
一般論とかたいそうな名前を付けました。
特に特別な環境下(体積一定、圧力一定など)を仮定しないという意味で「一般論」と呼んでいます。
具体的な話は(B)(C)を考えれば良いですが、それでは論理が飛躍してかえって誤解を招きますので、特に何も仮定をしない一般論を述べた後、具体的な状況下を考える方が良いと考えています。
熱力学状態は、温度\(T\)、圧力\(p\)、体積\(V\)などのうち独立な2つの変数を指定すれば良いのですよね。
なので、内部エネルギー\(U(T,V)\)については独立な変数として、温度\(T\)、体積\(V\)を指定することにします。
内部エネルギー\(dU\)の全微分を考えると、
と書けるので、(1)式に代入しましょう。
すると、(1)式は、
d^{\prime}Q=\bigg(\frac{\partial U}{\partial T}\bigg)_{V}dT+\bigg(\bigg(\frac{\partial U}{\partial V}\bigg)_{T}+p\bigg)dV\tag{3}
\end{align*}
となります。
(3)式が、左辺\(d^{\prime}Q\)のように加えられたエネルギーに対して、右辺の変数\(T\),\(V\)として変化する量となります。
これで一般論(A)の解説が終わりました(^^)
あとは、「(B)体積一定」「(C)圧力一定」の場合を考えることにしましょう。
この時にはじめて、定積比熱\(C_{V}\)や定圧比熱\(C_{p}\)という物性値を導入することになります。
気体定数\(R\)や定積比熱\(C_{V}\)や定圧比熱\(C_{p}\)のような、物性値は色々な物理量を結びつけるために導入した物質特有の量であって、それさえデータベースとして押さえておけば、あとはデータベースから引っ張り出して、便利なように異なる物理量を結びつけることができるのです。
例えば、「理想気体の状態方程式」は
\(pV=一定\)と\(V/T=一定\)から、\(p\),\(V\),\(T\)を結びつけるために気体定数\(R\)を導入したりしたが、こんな感じで導入されます。
※熱伝導率は物質特有の値であるため物性値と呼ばれますが、熱伝達係数は物質特有の値ではありません。
熱伝達係数は流れによって値が変わるからです。
このように、必ずしも物質特有の値とは限らないということには注意しておく必要があります
(B)体積一定の場合
体積一定なので、\(dV=0\)と考えれば良いので、(3)式より第二項がすべて消えてしまいます。
\end{align*}
特に、
\end{align*}
と置くとき、\(C_{V}\)を定積比熱と呼びます。
すなわち、(5)式が、
\end{align*}
のように書けることになります。
ここでの\(C_{V}\)定積比熱の単位は、\((J/mol K)\)です。
特に、両辺\(dT\)で割って、
\end{align*}
とすれば、
定積比熱は、「体積一定のもとで、1molあたり・1Kあげるのに必要なエネルギー」と解釈することができます。
※体積一定なので添え字で\(V\)と表記しました。
前段の説明でもしましたが、体積膨張しないので加えられた熱量が全て内部に蓄えられるエネルギーになります。
(C)圧力一定の場合
圧力一定なので、圧力\(p(T,V)=一定\)とすることができます。
ここで、\(T\)の変化に伴って容積\(V\)が変化するので、
このように書けば、(3)式は、
ここで、
より、(7)を用いて、
nC_{p}=\bigg(\frac{\partial U}{\partial T}\bigg)_{V}+\bigg(\,\bigg(\frac{\partial U}{\partial V}\bigg)_{T}+p\bigg)\,\bigg(\frac{\partial V}{\partial T}\bigg)_{P}\tag{9}\end{align*}
と置くとき、\(C_{p}\)を定圧比熱と呼びます。
$\big(\frac{d^{\prime}Q}{dT}\big)_{p}=nC_{p}$から導いても良い。
※体積一定なので添え字で\(p\)と表記しました。
これは圧力一定(定圧)のもとで、導入した定数と言う意味で定圧比熱と呼ばれている。
ちなみに(9)式は、下記のように書いている場合もありますのでご注意を。
(9)式と見比べてみてください。
何を固定しているかの表記が違います。
(9.1)は明らかに、圧力を固定するいうのを明記しているので、
熱力学第一法則(\(d^{\prime}Q=dU+pdV\))を圧力を固定したまま、温度\(T\)で割るだけで(9.1)になります。
ちなみに(15)式から、(15.1)式も表記は違えど、同じことを意味していますので、(9.1)式から(9)式を導出できるはずです。
(9.1)式の、\((\frac{\partial U}{\partial T})_{p}\)に対して、内部エネルギー\(U\)を変数\(T,V\)として、単に偏微分を\(V\)固定で行うだけです。
\end{align*}
を(9.1)式に代入すると、(9)式になります。
また、エンタルピー\(H=U+pV\)を用いて、
\(nC_{p}=\big(\frac{dH}{dT}\big)_{p}\)と書くこともできます。
なぜなら、エンタルピーの全微分を書くと
\end{align*}
となります。
定圧を考えているので、\(dp=0\)なので最後の項は0です。
また、熱力学第一法則より、
\end{align*}
なので、
\end{align*}
となり、圧力一定の元で温度を1K上げるのに必要な熱量は、
\(\big(\frac{d^{\prime}Q}{dT}\big)_{p}\)であるので、
\end{align*}
となります。
(A)(B)(C)のまとめ
熱力学第一法則から定積比熱と定圧比熱の定義を行いました。
大事なのは「(A)一般論」では定積比熱\(C_{V}\)、定圧比熱\(C_{p}\)も一切登場していません。
定積比熱と定圧比熱はどのように定義したかを理解しておきましょう。
定圧比熱と定積比熱の表式についてまとめました。
| No. | 環境下 | 0の変化量 | 比熱の色々な表記 |
| A | 圧力も体積も変化 | – | – |
| B | 体積一定 | \(dv=0\) | \(C_{V}\):定積比熱 \(C_{V}\):定積比熱の単位は、\((J/mol \,K)\)
体積一定下において、1mol当たり、1K(もしくは1℃)上昇させるのに必要な熱量(J) |
| C | 圧力一定 | \(dp=0\) | \(C_{p}\):定圧比熱 \(C_{p}\):定圧比熱の単位は、\((J/mol \,K)\)
圧力一定下において、1mol当たり、1K(もしくは1℃)上昇させるのに必要な熱量(J) |
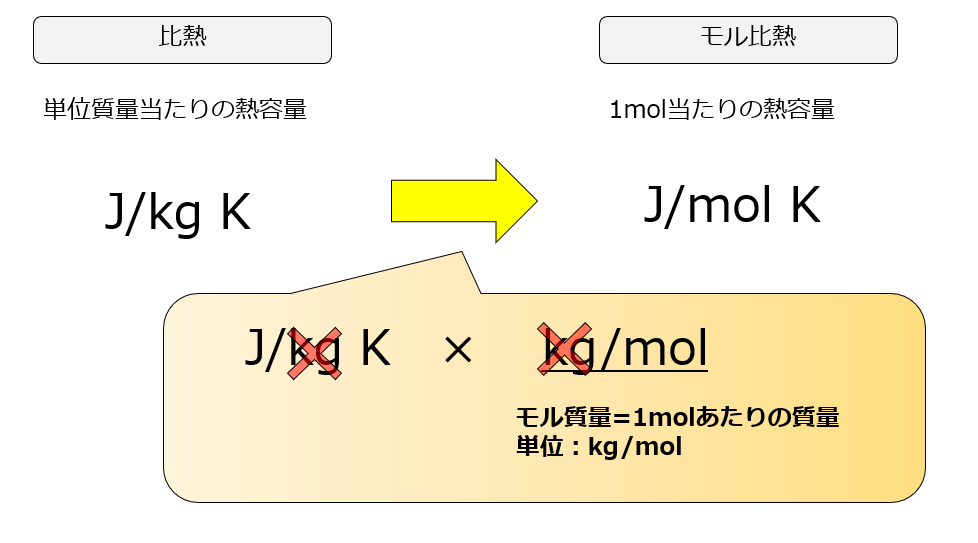
比熱の単位が1mol当たり1℃上昇するのに必要なエネルギー[J/mol K]で定義しているのか、単位質量当たり1℃上昇するのに必要なエネルギー[J/kg K]で定義しているのか、分野によって向き不向きがあるので、参考書を読む際は単位には十分に注意しましょう。
比熱には温度依存性がある!理論的にまとめました。
- 内部エネルギーとは何か?
【理想気体の比熱の温度依存性(1)】内部エネルギーとは。
- 古典近似での比熱の理解の誤り
【理想気体の比熱の温度依存性(2)】分配関数から物理量の期待値が求まる。
【理想気体の比熱の温度依存性(3)】分配関数の古典近似を考えてみよう。
【理想気体の比熱の温度依存性(4)】古典近似から2原子分子の比熱を求める。
【理想気体の比熱の温度依存性(5)】2原子分子の回転の運動にもエネルギーが等分配されているのか。 - 量子論(+統計力学)での比熱の取り扱いと正しい理解
【理想気体の比熱の温度依存性(6)】2原子分子のシュレディンガー方程式
【理想気体の比熱の温度依存性(7)】シュレディンガー方程式の極座標表記(2原子分子)
【理想気体の比熱の温度依存性(8)】量子論でエネルギー固有値から2原子分子の比熱を計算する
比熱の温度依存性を理解する理論的な面白さは以下にあります。
お勧めの参考書
「なぜ比熱の温度依存性があるのか」について、
- 熱力学
- 量子力学
- 統計力学
この3つの知識が必要になります。
熱力学
比熱の理解は、やはり熱力学から勉強しないといけません。
そんな中どの「熱力学」の参考書で勉強すればよいのかというと、以下の2冊が絶対おすすめです。
こちらの2冊を読むと熱力学の見方が変わります!!
量子力学
比熱の理解には量子力学の知識が絶対に必要になります。
量子力学の計算をとても丁寧に解説した参考書が以下になります。
特に「2原子分子のシュレディンガー方程式」についての解説や、「シュレディンガー方程式の極座標表記」については、下記の参考書はとても役に立ちます。
統計力学
統計力学は特に「統計力学Ⅰ」の参考書が比熱の理解には大いに役に立ちます。
量子力学の知識がある方は読み進めることができると思います。
























(9.1)式から(9)式導出の際の(dU/dT)pの偏微分の際にp一定の条件が消えたように思うのですが、なぜでしょうか。
コメントありがとうございます。
誤記がありましたので修正しました。
ご指摘ありがとうございます。