どうも(^^)/
本日はタイトル通り、断熱過程では系が外部にする仕事は操作の仕方によらないというのを示したいと思います。
熱力学では、等温過程と断熱過程というのがありますが、それと系が外部にする仕事との関係性をまとめてみましょう。
| 等温過程 | 断熱過程 | |
| 説明 |
熱力学第一法則 \(Q=\Delta U +W\) ↓ 等温過程では\(\Delta U=0\)となる。 ↓ \(Q=W\) ※理想気体で内部エネルギーが、 温度にしか依存しないことは下記の記事で示しています。 |
熱力学第一法則 \(Q=\Delta U +W\) ※\(W\)は気体が外部にする仕事 ↓ 断熱なので\(Q=0\) ↓ \(\Delta U=-W\) |
| 結論 |
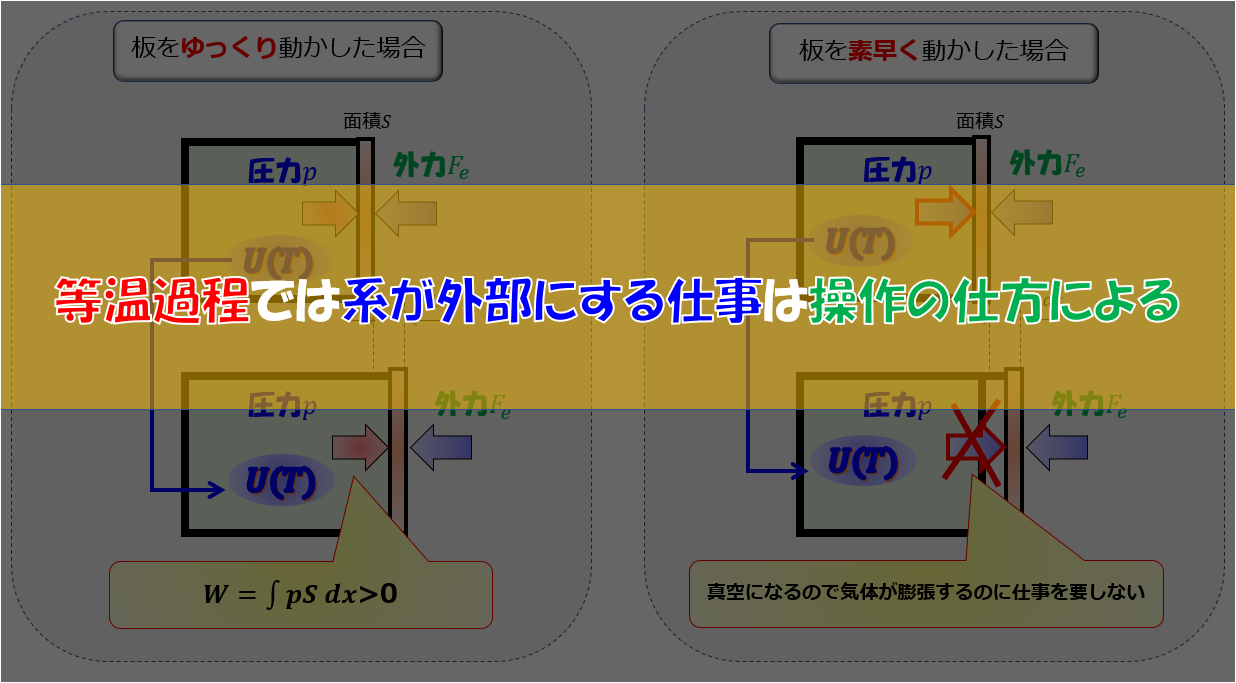
等温過程では、 系が外部にする仕事は操作の仕方による。 |
内部エネルギーは状態量なので、 系が外部にした仕事の過程に依らず、 始点と終点だけの状態量だけで決まる。 |
断熱過程では系が外部にする仕事は操作の仕方によらない
前回は、等温過程では系が外部にする仕事は操作の仕方によるという話をしました。
しかし、断熱過程では系が外部にする仕事は操作の仕方によらないのです。
これを示すのはとても簡単です。
熱力学の第一法則
Q=\Delta U +W\tag{1}
\end{align*}
※\(Q\):正味の熱量
※\(\Delta U\):内部エネルギー変化
※\(W\):系(気体)が外部にした仕事量
断熱過程であるので、熱量の出入りがないということですよね。
とういうことは\(Q=0\)です。
つまり、
0=\Delta U +W\tag{2}
\end{align*}
です。
ちょっと式を変形すると、
W=-\Delta U\tag{3}
\end{align*}
この時点でわかるかと思いますが、内部エネルギーは状態量であったわけですよね。
状態量であればどういうことになるのかというと、
ある操作を通して熱力学のマクロな物理量である圧力\(p\)や温度\(T\)などが定義できる状態になれば、定義できるわけです。
つまり、内部エネルギー\(U\)変化は、ある操作の始点と終点の差\(\Delta U\)
\Delta U=U_{2}-U_{1}
\end{align*}
と書けるのです。
ということは、
異なる操作があり、その操作がどんなに違ったとしても、最初の状態と最終の状態さえ同じであれば、あるいは内部エネルギー状態の差が同じであれば、
W=-\Delta U\tag{3}
\end{align*}
この(3)式より、系(気体)が外部にする仕事は同じです。
ゆっくり1回動かす場合と、ゆっくり2回動かす場合
簡単な例を見てみます。
次の異なる操作を考えます。
- ゆっくり1回動かす場合
- ゆっくり2回動かす場合
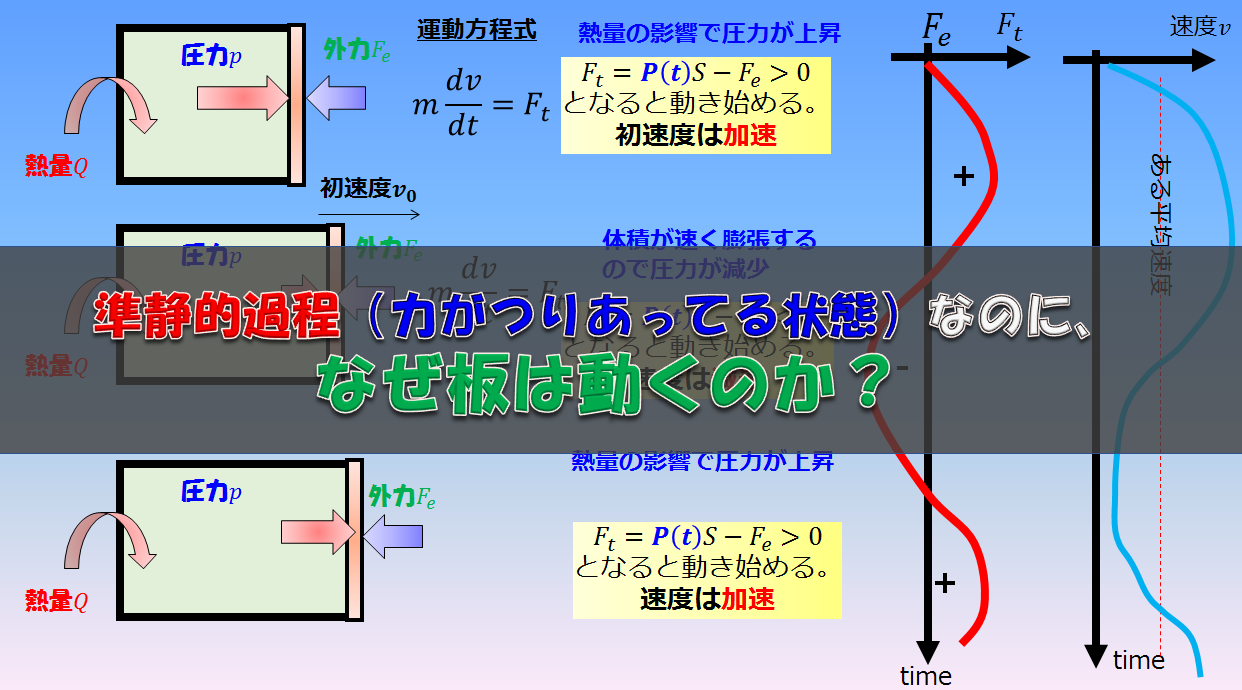
※ゆっくり動かすというのがミソです。
ここでのゆっくりとは、準静的過程であるという意味です。
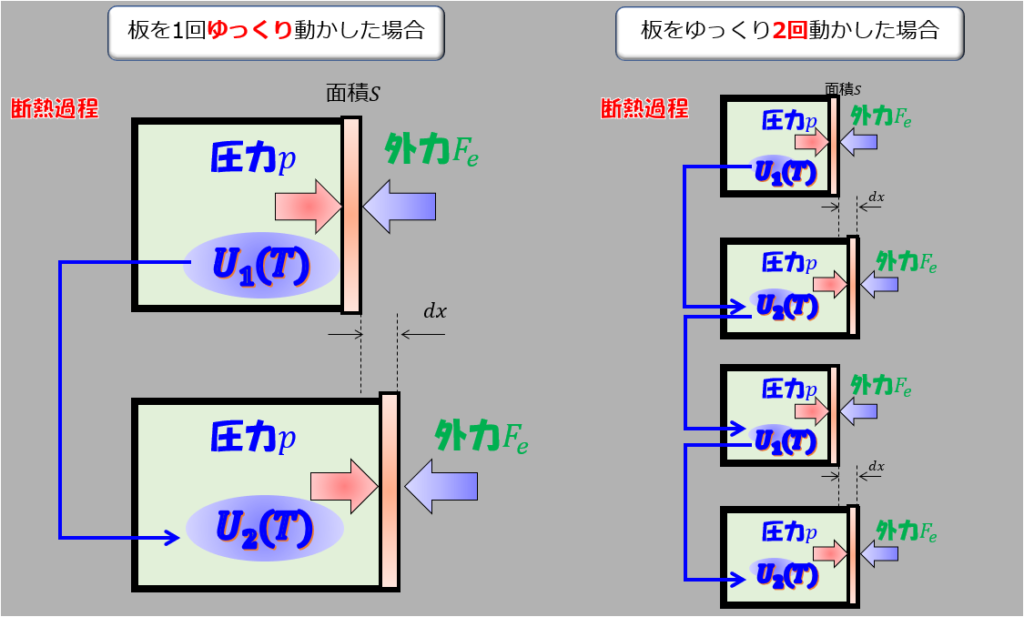

このようにゆっくり1回動かそうが、2回動かそうが、複数回動かそうが・・・・・
最初と最後の内部エネルギー差\(\Delta U=U_{2}-U_{1}\)に変わりはないのですから、
結局、系(気体)が外部にする正味の仕事量は、
W=-\Delta U\tag{3}
\end{align*}
となります。
このように、断熱過程では系が外部にする仕事は操作の仕方によらないのです(^^)/
誤解があるといけないので補足をしておくと、ゆっくり(準静的)だから、系(気体)が外部にした仕事が操作の仕方によらなかったというわけではなく、
最初と最後の状態(内部エネルギー差)だけで、系(気体)が外部にした仕事が決まるということに注意しましょう(^^)/
ゆっくり動かした理由は、板を引く場合と押す場合の操作によって、もとの状態に戻せるからそのような操作(可逆的)を行っただけです。
別にゆっくり動かしたというのは、今回の話では本質的な事ではなかったということですね。
まとめ
断熱過程では系が外部にする仕事は操作の仕方によらないというのを示しました(^^)/
ところで、以下のように・・・・断熱にしておいて
- 板を素早く引く(気体がついてこれないくらい)
- その後板をゆっくり元の容器の大きさまで圧縮する
とするとどうなるでしょうか?
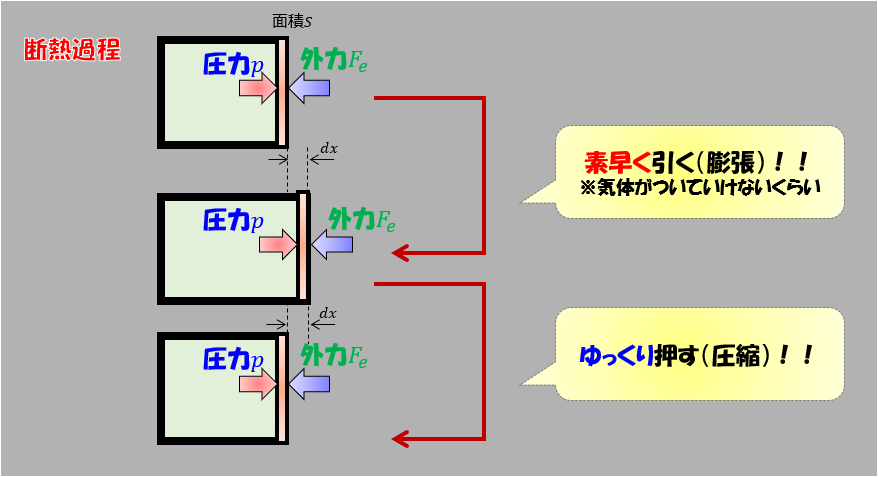

答えは「最終の温度は、初期の温度よりも上がる」です(‘ω’)
というわけで次回をお待ちください(‘ω’)ノ