こんにちは(@t_kun_kamakiri)。
本記事では前回の記事で話すことができなかった準静的過程というのを話していきます。
まず準静的過程とは何か?
系が熱力学的平衡の状態を保ったまま、ある状態から別の状態へとゆっくり変化する過程を指す熱力学上の概念
この文言から、熱力学という学問の中での概念上の話であることがわかります。
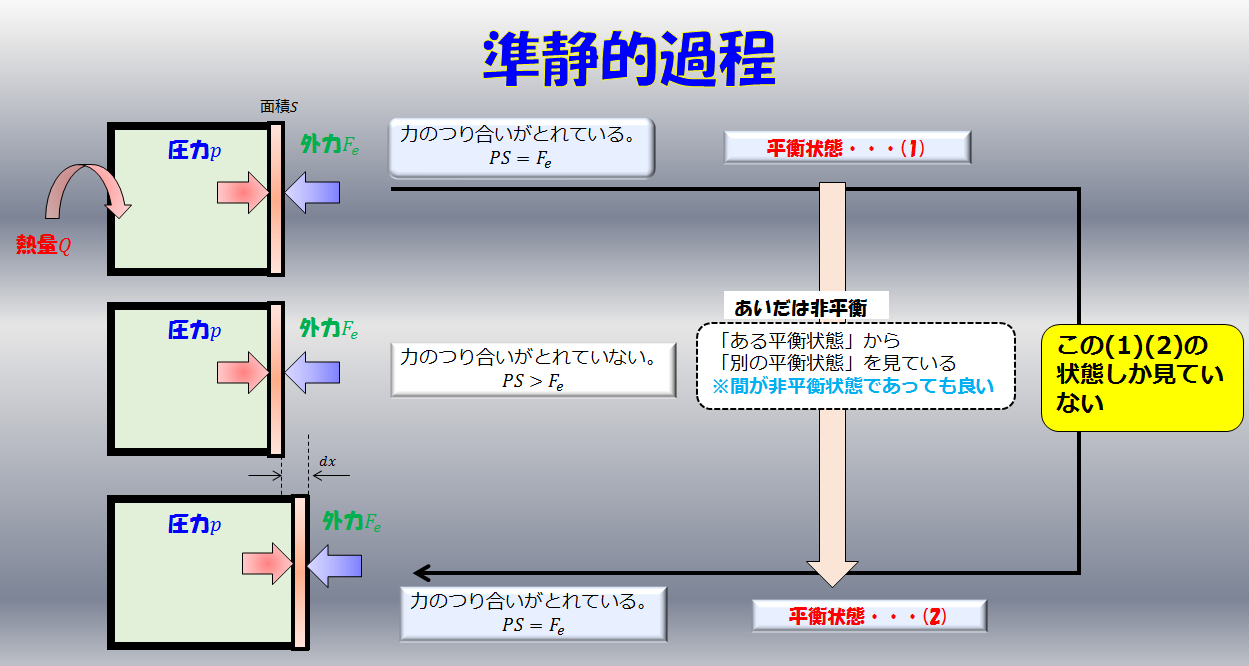
準静的過程
例えば下記のように、「熱量」を加えて気体の温度を上昇させます。
そうすると、板は徐々に右へゆっくりと動き出します。
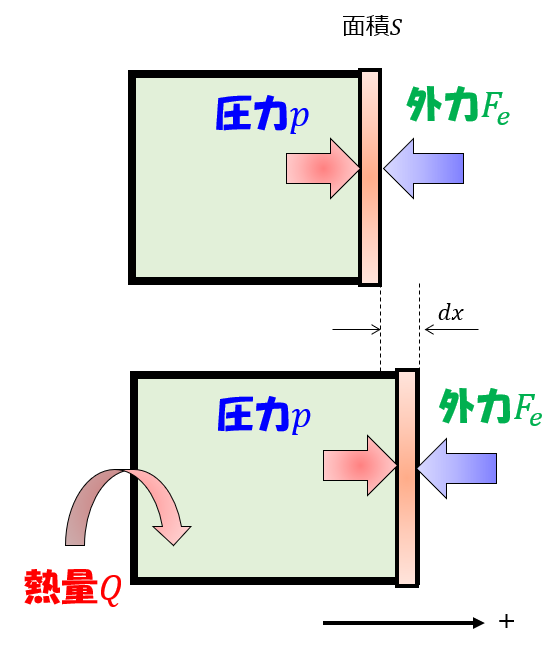
力のつり合いをとてた状態で決して焦らずゆっくりと板を押します。
このような常に熱平衡状態が保たれていると近似できるような過程のことを準静的過程と言います。
熱平衡状態とは、「マクロな物理量である、圧力、温度など」が定まっている状態です。
なので、気体の圧力が定義できているので、力学的な力のつり合いを立てることになります。
pS-F_{e}=0(pS=F_{e})
\end{align}
となります。
だから、これを仕事量に置き換えると、
pSdx-F_{e}dx = 0\cdot\cdot\cdot (1)
\end{align}
W-W_{e} = 0\cdot\cdot\cdot (2)
\end{align}
となるので・・・・
気体(系)がする仕事量=外部が(系に)する仕事
が言えるということですね。
要するに、常に平衡状態を保っていて、気体がする仕事量も外部がする仕事量も同じ状況だから、
熱力学の第一法則を・・・
熱量=内部エネルギー+気体(系)がする仕事量・・・(1)
と書いても・・・
内部エネルギー=熱量+外部が(系に)する仕事・・・(2)
と書いても良かったわけです。
しかし・・・
熱力学は「ある平衡状態」から「別の平衡状態」しか見ていない!!
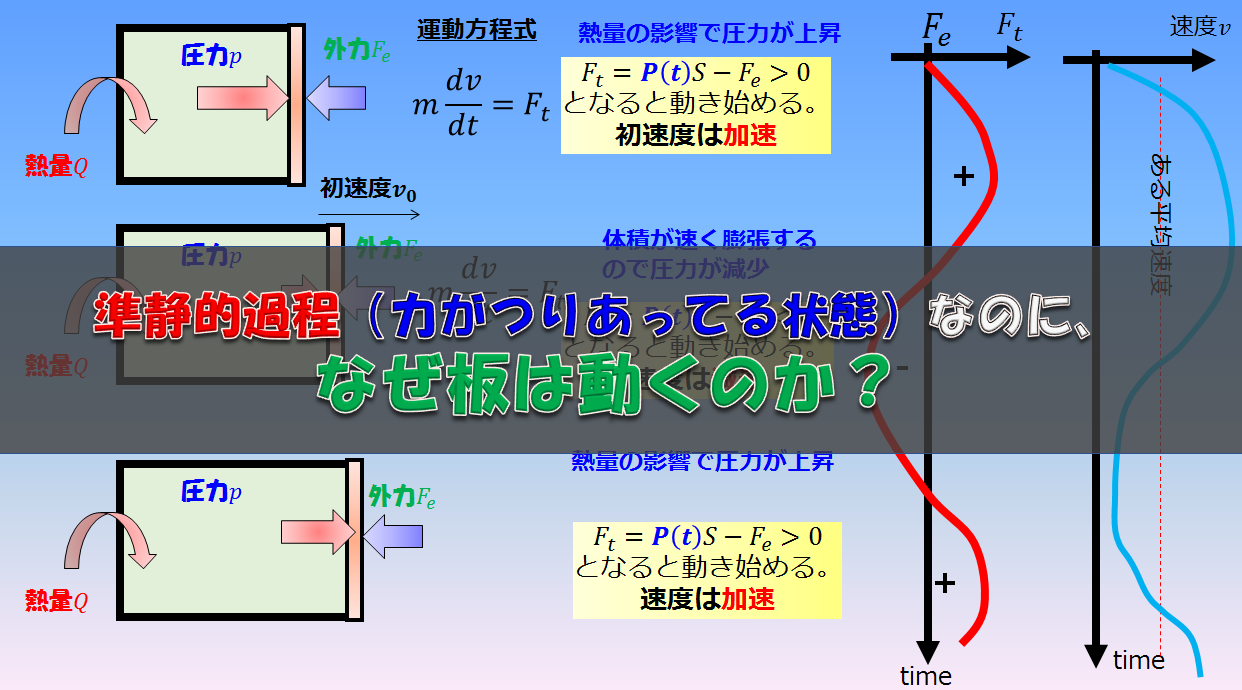
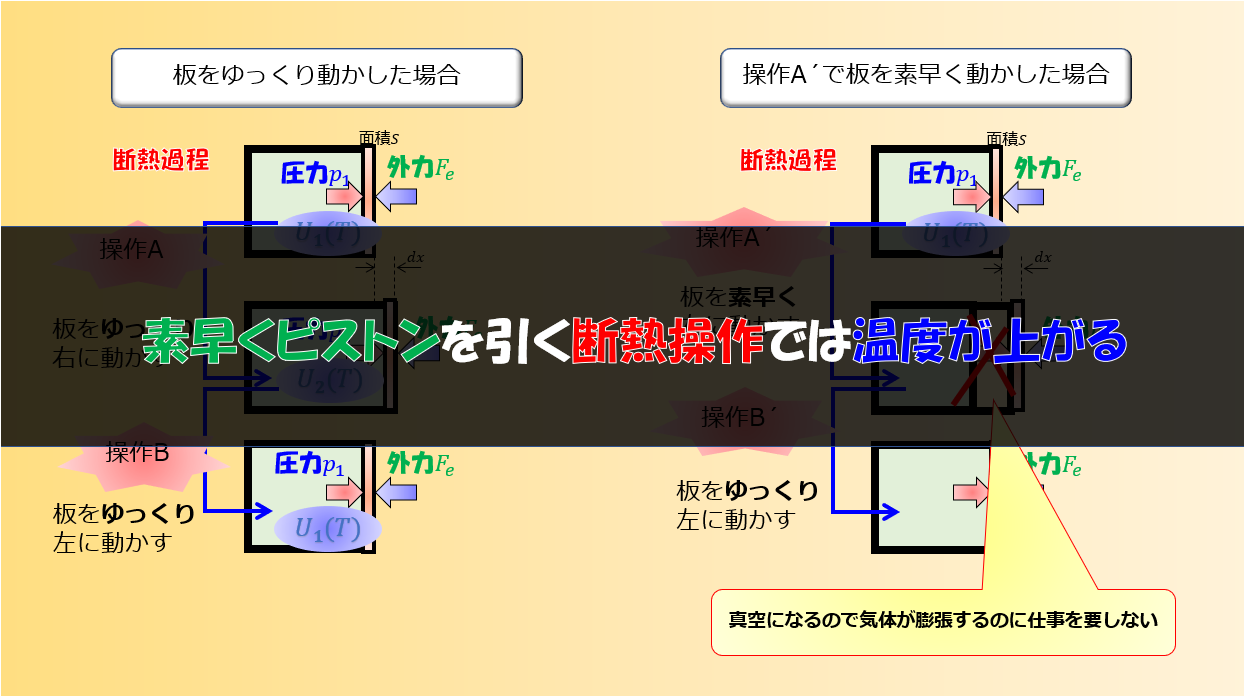
なんで力のつり合いがとれているのに、動くのかが気になったのでちょびっと考えました。
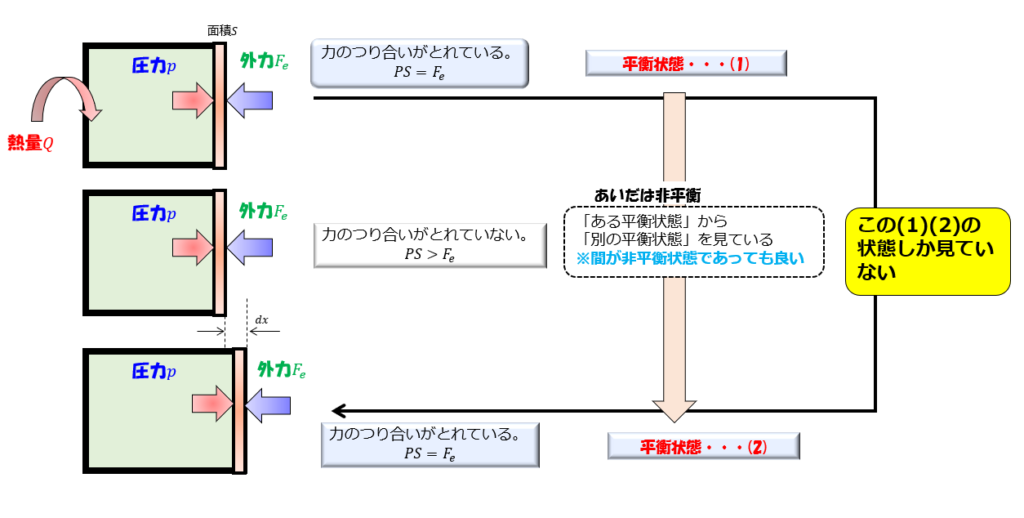
熱力学は「ある平衡状態」から「別の平衡状態」しか見ていない!!
これが、わかりやすい言い方だと思いました(^^)/
最初にある熱平衡状態を保った系があったとします。そこに熱を加えることを考えます。
具体的には、上の絵のように熱を加えます。
そうすると、気体の温度が上昇して板を動かし始めるでしょう。
その瞬間には、あるところでは温度が高く、あるところでは温度が低いといった、その系におけるマクロな物理量などが定義できなくなります(部分的にはできるけど・・・)
しかし、板を押すとまた外力と釣り合う圧力になり、新しい平衡状態となります。
そして、間が「非平衡状態」だろうがなんだろうが、その間隔が無視できるくらい無限にゆっくり繰り返せば、力のつり合いがとれた状態で板が動くということになります。
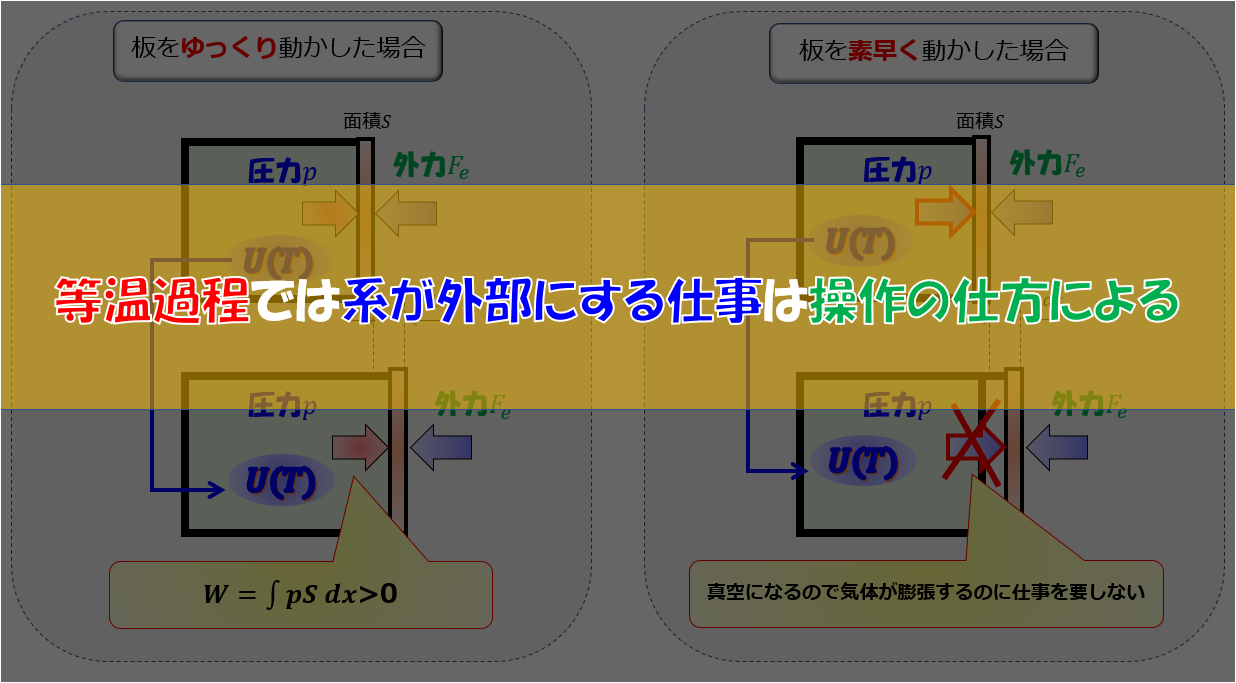
現実問題で、むちゃくちゃゆっくりなんてできるのか?
これだと現実味のない話になってしまいます。
無限にゆっくりと言われても、結局は何に対してゆっくりかということを明確にしておきたいところです。
こちらの記事で書いたように、微小な圧力変化(密度変化)などの伝播速度は、音速で伝わるということが示されます。
ということは、音速と比較して十分ゆっくりであれば、近似的に「無限にゆっくり」として取り扱っても良いということ・・・・・でしょう。
熱力学おすすめの参考書
熱力学のおすすめの参考書はこちらの記事に書いています。
選ぶのが面倒って方はこの↓2冊を読んでいれば間違いないと思います。