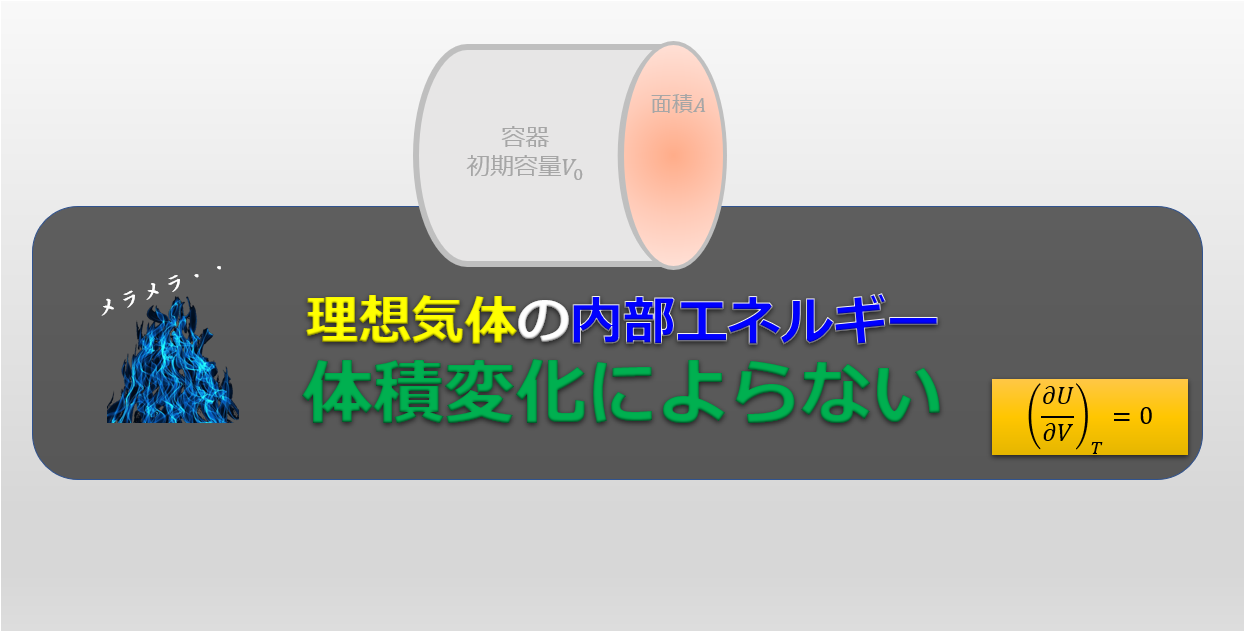
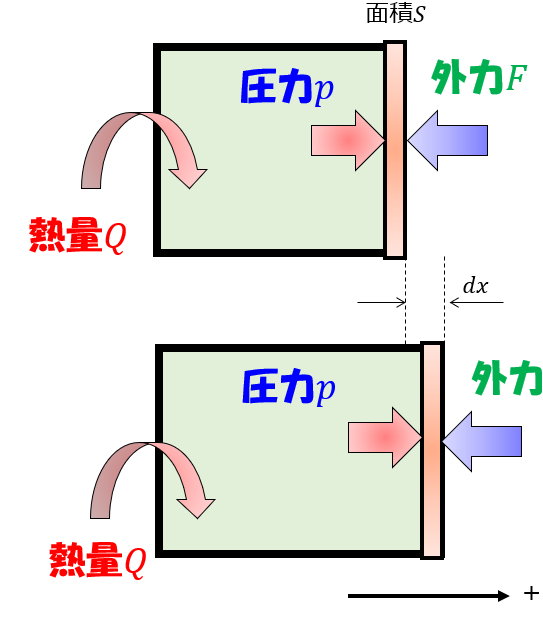
前回の記事で準静的過程というのを説明しました。
準静的過程とは、簡単におさらいをしておくと・・・
系が熱力学的平衡の状態を保ったまま、ある状態から別の状態へとゆっくり変化する過程を指す熱力学上の概念
と、このように熱力学の概念上の話で、下記のように板をはさんで「気体(系)と外部の力がつりあっている状態で無限までゆっくりと動かすことで熱平衡状態を保ったまま板はゆっくりと動く」というものです。
つまり・・・
F_{t}=pS-F_{e}=0\cdot\cdot\cdot (1)
\end{align*}
です。
しかし、疑問が・・・・
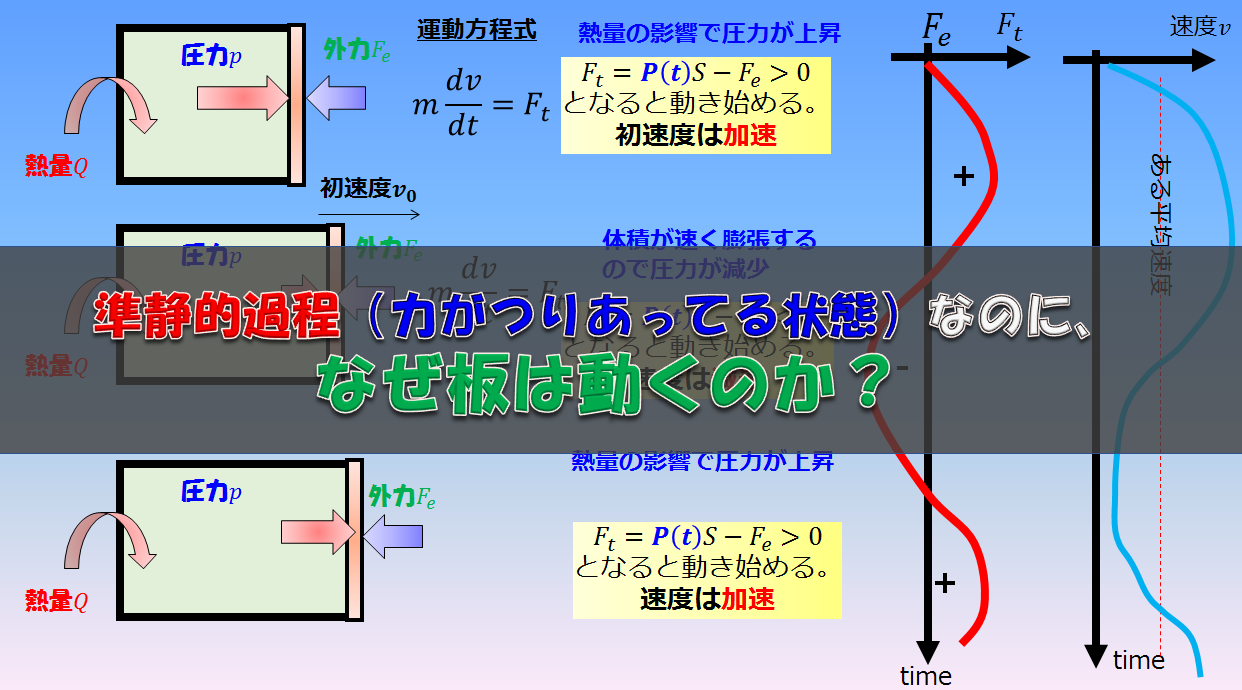
力がつりあっているのにどうして板が動くのか?
もし板の運動方程式を考えるなら・・・
m\frac{dv}{dt}=F_{t}\cdot\cdot\cdot (2)
\end{align*}
板が静止している状態からスタートして\(F_{t}=0\)なら板が動かないのではないか・・・この疑問に対して、少しでも回答を得れればと思います(^^)/
もし、板の運動方程式を考えるのであれば
あまり急激に外から熱を加えると、急激に圧力が高くなるので、じんわり熱を外部から加えていく状況を考えます。
板にかかる摩擦の影響、重力の影響などを無視して、板の運動方程式を考えてみましょう。
※板の質量:\(m\)
運動方程式
m\frac{dv}{dt}=F_{t}\tag{3}
\end{align*}
※板の質量:\(m\)
※\(F_{t}=p(t)S-F_{e}\)(外力一定:\(F_{e}\))
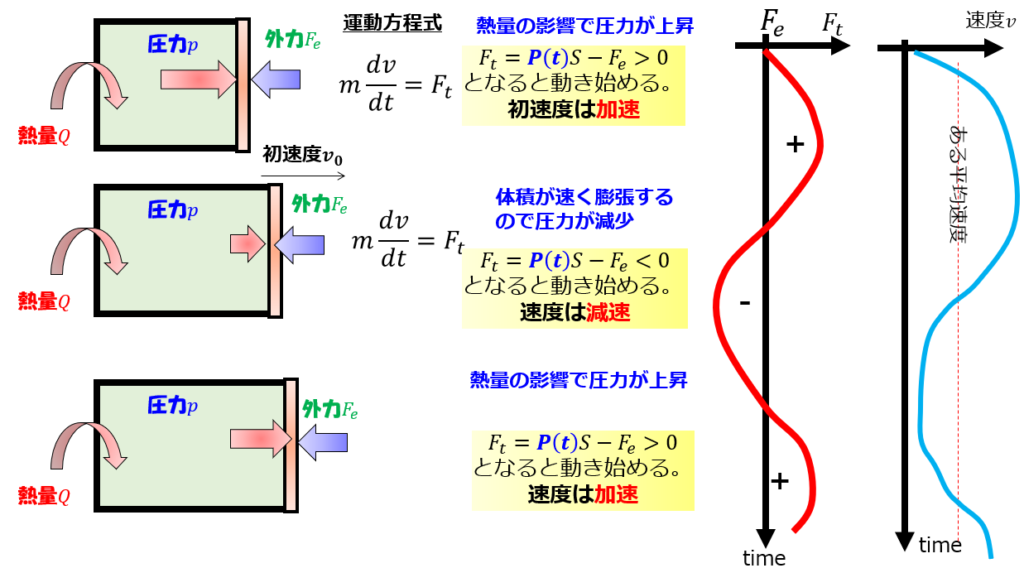
力がつりあっている状態であっても、初速度を一旦与えてやれば、そのまま動きますよね。
上の絵を見ていただければわかるように、準静的過程とは・・・
初速度\(v_{0}\)を持つのですが、ほとんど\(P(t)S-F=0\)であるような状態を考えているので、\(v_{0} \rightarrow 0\)であるような状況ということになります。
これが、準静的過程でゆっくり動かしているという近似的な状況です。
めちゃくちゃゆっくりではなく、まあまあゆっくりならどうなるか?
では、めちゃくちゃゆっくりではなくて、「例えば、1m/s」くらいのオーダーで動かすと理論上はどうなっていることになるのか?
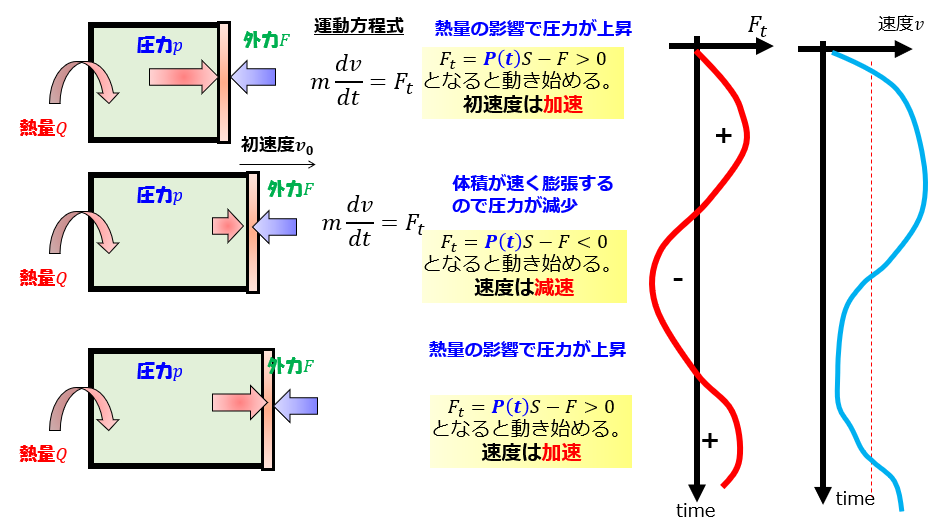
これは上の絵のように振動している状況になるでしょう。
- 「熱を加えられて圧力が上昇」⇒「板は加速しながら動く」
- 「熱量よりも体積膨張の方が速いため圧力減少」⇒「板の速度は減速」
- 「またまた熱量により圧力が増加」⇒「板は加速する」
この「1→2→3(1と3は同じ状況)」を繰り返しながら、
圧力\(p(t)\)は、外力のあたりを振動し、速度はある速度のあたりで振動する・・・ということが考えられます。
つまり、振動する波形を描いてくれるはずだ!!と・・・
定性的には、「外力が大きければ、または加える熱量が小さい」ならば、振動の振幅は小さくなり、「板のある速度」の値は小さくなることが予想されます。
「外力が大きければ、または加える熱量が小さい」の程度がより強調される状況下であると、準静的に近づくのですから、そのような予想がたつというわけです。
本当に振動するのか?
本当はどうなっているのかは、方程式を立てて、それを解いてあげればよい。
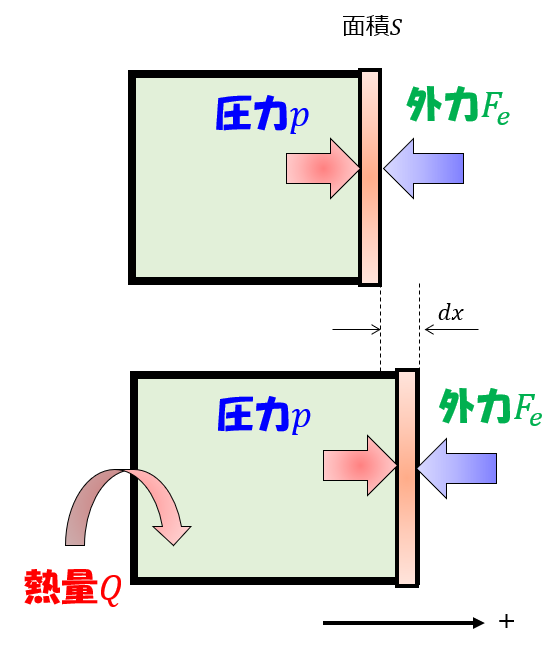
この絵を見て、「熱力学の第一法則」と「力学における運動方程式」、さらには「理想気体の状態方程式」をコラボさせれば良いでしょう。
※簡単のため、加える熱量\(Q\)は一定とします。
※板にはたらく摩擦力は無し
※熱の損失も無し
熱力学第一法則
Q=\Delta U+W
\end{align*}
気体が外にする仕事量を\(W=\int ^{x_{0}+\Delta}_{x_{0}}pS dx\)として、微小区間\(\Delta x \rightarrow dx\)とすると、
d^{‘}Q=dU+d^{‘}W
\end{align*}
この、\(d^{‘}W=pS dx\)として、微小時間で気体がした仕事量を\(\frac{d^{‘}W}{dt}=pS\frac{dx}{dt}\)と置くことで、
\frac{d^{‘}Q}{dt}=\frac{dU(t)}{dt}+pS\frac{dx(t)}{dt} \tag{4}
\end{align*}
気体のする仕事\(W\)
W=\int^{x+\Delta x}_{x}pSdx
\end{align*}
ここで、\(\Delta x \rightarrow dx\)としています。
板の運動方程式
m\frac{dv(t)}{dt}=p(t)S-F_{e}\tag{5}
\end{align*}
理想気体の状態方程式
p(t)=(\gamma-1)\frac{U(t)}{V(t)}\tag{6}
\end{align*}
ちなみに、容量変化と板の移動量の関係式として、
\frac{dV(t)}{dt}=S\frac{dx(t)}{dt}\tag{7}
\end{align*}
V(t)=(x(t)+x_{0})S\tag{7.1}
\end{align*}
であることをお忘れなく。
(4)(5)(6)を連立させて解くことになります。
(4)と(6)を使って\(U(t)\)を消去
(6)式より、
U(t)=\frac{p(t)V(t)}{\gamma-1}\tag{8}
\end{align*}
これを、(4)式に代入します。
Q=\frac{1}{\gamma-1}\bigg(p(t)\frac{dV(t)}{dt}+V(t)\frac{dp(t)}{dt}\bigg)+p(t)\frac{dV(t)}{dt}\tag{9}
\end{align*}
さらに(9)式を整理します。
\gamma p(t)\frac{dx(t)}{dt}+(x(t)+x_{0})\frac{dp(t)}{dt}=A\tag{10}
\end{align*}
板の運動方程式(5)式に、(7)(7.1)式を用いてやると、
m\frac{d^2 x(t)}{dt^2}=p(t)S-F_{e}\tag{11}
\end{align*}
\(A=\frac{(\gamma-1)Q}{S}=const\)
CAE解析ソフトを使ってシミュレーション
(10)(11)式を数値計算で解くのはめんどうなので、CAE解析ソフトを使って実行してみます。
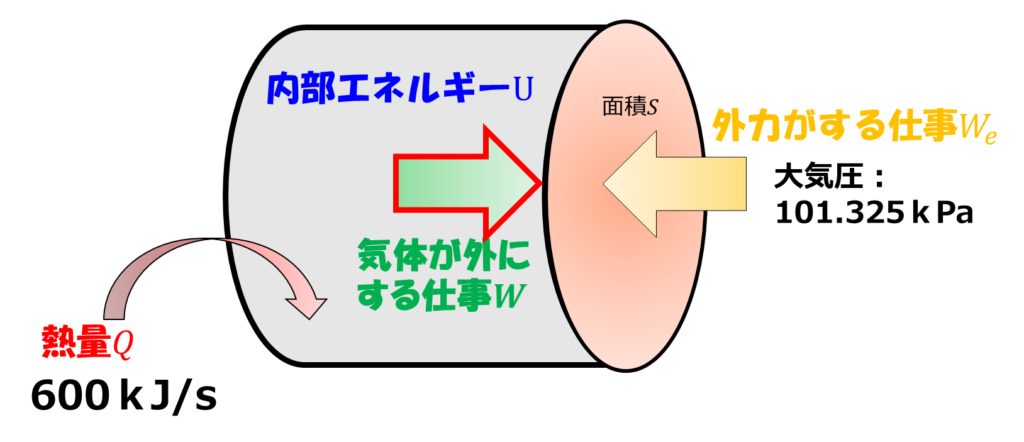
解析条件
- 外部から熱量:600kJ/s(一定)を加える
- 大気圧:101.325kPa←これが外力になる
- ※熱の逃げなどは無いものとする。
解析の結果
では解析の結果を示しましょう。
↓動画はこちら
はい。動画を見てもよくわかりませんが・・・・
速度と圧力を見てみましょう!
板の速度
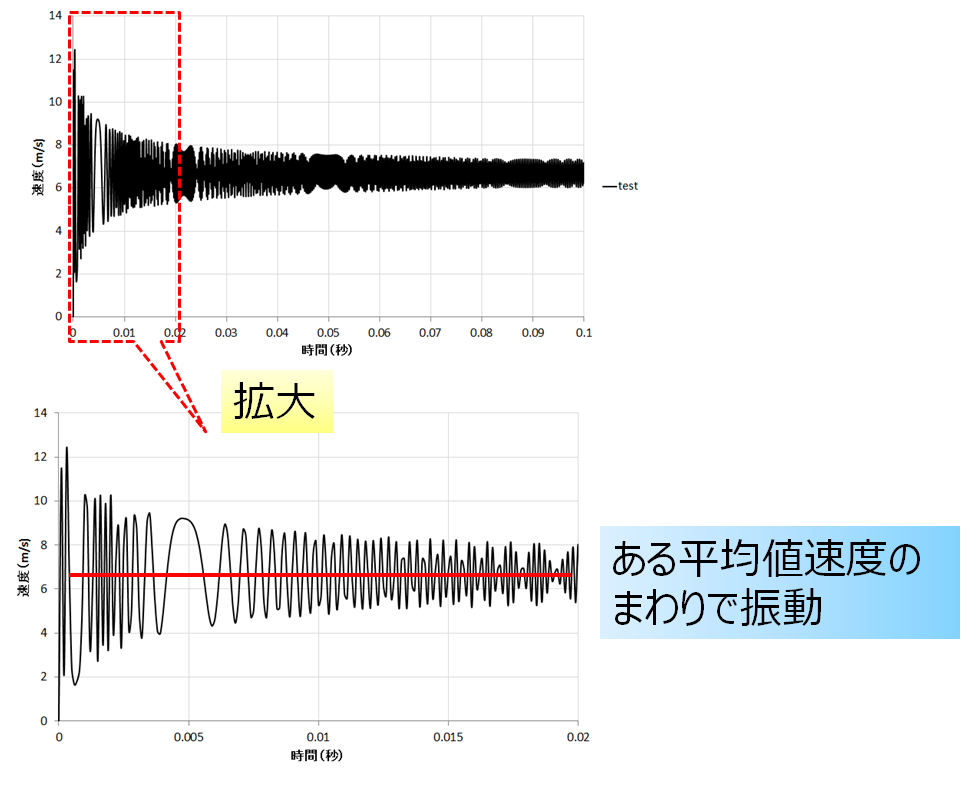
気体(系)の圧力

やはり大気圧(外部と同じ圧力)のまわりで振動していますね。
果たしてこの振動が意味のある振動なのでしょうか?
微小振動に意味はあるのか?むちゃくちゃゆっくりなんてできるのか?
準静的過程では、「無限にゆっくり」と言われます。
上で示したシミュレーションは特に無限にゆっくりかどうかはわかりません。
拡大したらちゃんと振動しているように見えるし、何よりシミュレーションの動画は無限にゆっくりではなくて、普通に7m/sで動いている結果となっています。
無限にゆっくりと言われても、結局は何に対してゆっくりかということを明確にしておきたいところです。熱平衡状態が常に成立しているとは、「圧力の不均一で定義できない領域がない状態」を意味しています。
圧力がわずかに変動した際に、その変動具合がどれくらいの速度で周囲に伝播するかがキーになりますね。
では、その微小な圧力変動はどれくらいの速度で伝播するのかというと、流体力学では圧力の微小変化は音速で伝播します!
つまり、無限にゆっくりとは、音速と比較してゆっくりかどうかということですね。
こちらの記事で書いたように、微小な圧力変化(密度変化)などの伝播速度は、音速で伝わるということが示されます。
音速と比較して十分ゆっくりであれば、近似的に「無限にゆっくり」として取り扱っても良いということ・・・・・でしょう。
先ほどCAE解析で示した速度の振動は、音速と比較して十分小さければ対して気にするレベルではないですし、そもそも解析のタイムステップ\(\Delta t\)を変えるだけで振動の具合が変わってしまうでしょう。

熱力学の第一法則では、微小区間における圧力が一定としているのに、運動方程式で圧力の時間変化を与えているので、数値的に振動しいるだけな気がします・・・・なので、マクロな視点をもって・・・振動をしていることが重要な情報ではなくて、その平均値に意味があるのだと考えられます。
熱力学おすすめの参考書
熱力学のおすすめの参考書はこちらの記事に書いています。
選ぶのが面倒って方はこの↓2冊を読んでいれば間違いないと思います。