どうも(^^)/
本日はタイトル通り、等温過程では系が外部にする仕事は操作の仕方によるというのを示したいと思います。
熱力学では、等温過程と断熱過程というのがありますが、それと系が外部にする仕事との関係性をまとめてみましょう。
| 等温過程 | 断熱過程 | |
| 説明 |
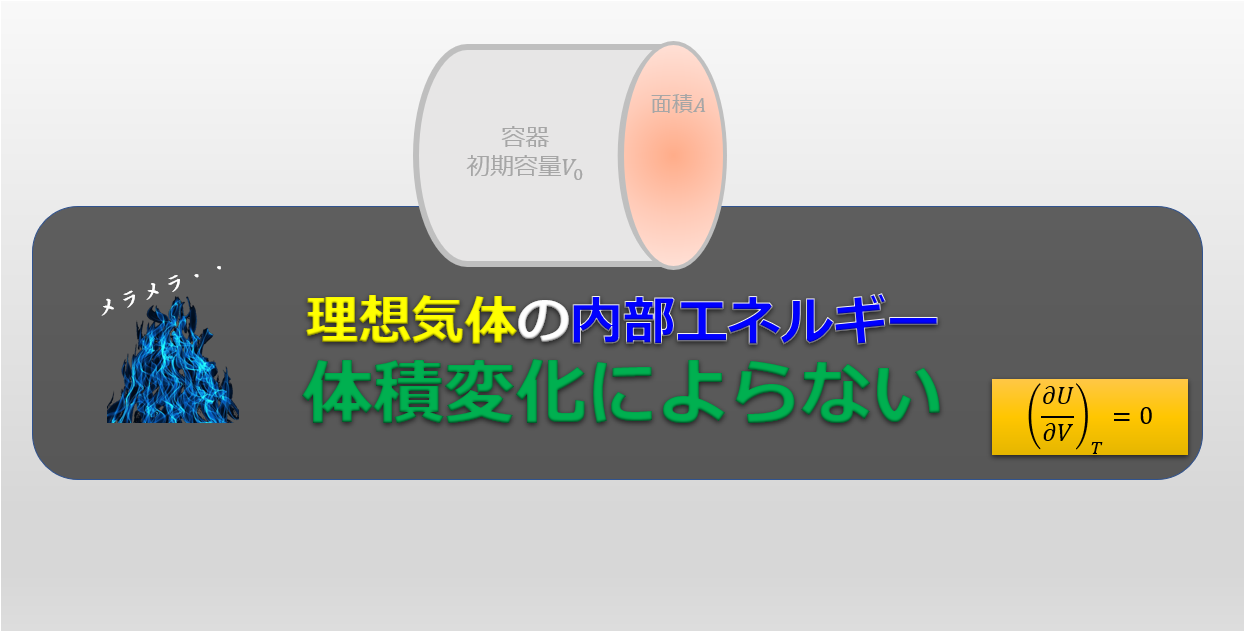
熱力学第一法則 \(Q=\Delta U +W\) ↓ 等温過程では\(\Delta U=0\)となる。 ↓ \(Q=W\) ※理想気体で内部エネルギーが、 温度にしか依存しないことは下記の記事で示しています。 |
熱力学第一法則 \(Q=\Delta U +W\) ※\(W\)は気体が外部にする仕事 ↓ 断熱なので\(Q=0\) ↓ \(\Delta U=-W\) |
| 結論 | 等温過程では、
系が外部にする仕事は操作の仕方による。 |
内部エネルギーは状態量なので、
系が外部にした仕事の過程に依らず、 始点と終点だけの状態量だけで決まる。 |
系とは何か?
系が外部にする仕事と言われると少々抽象的ですので、
と簡単に考えておきましょう。
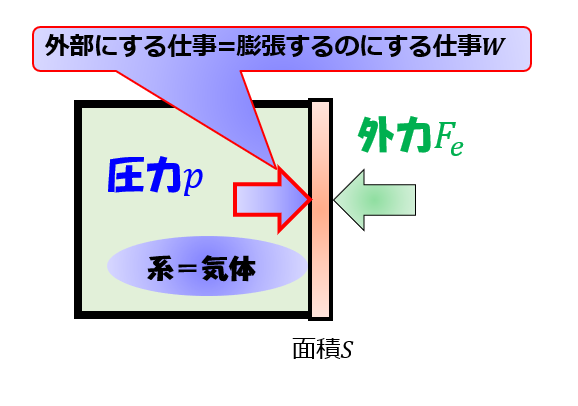

操作の仕方を2通り考える
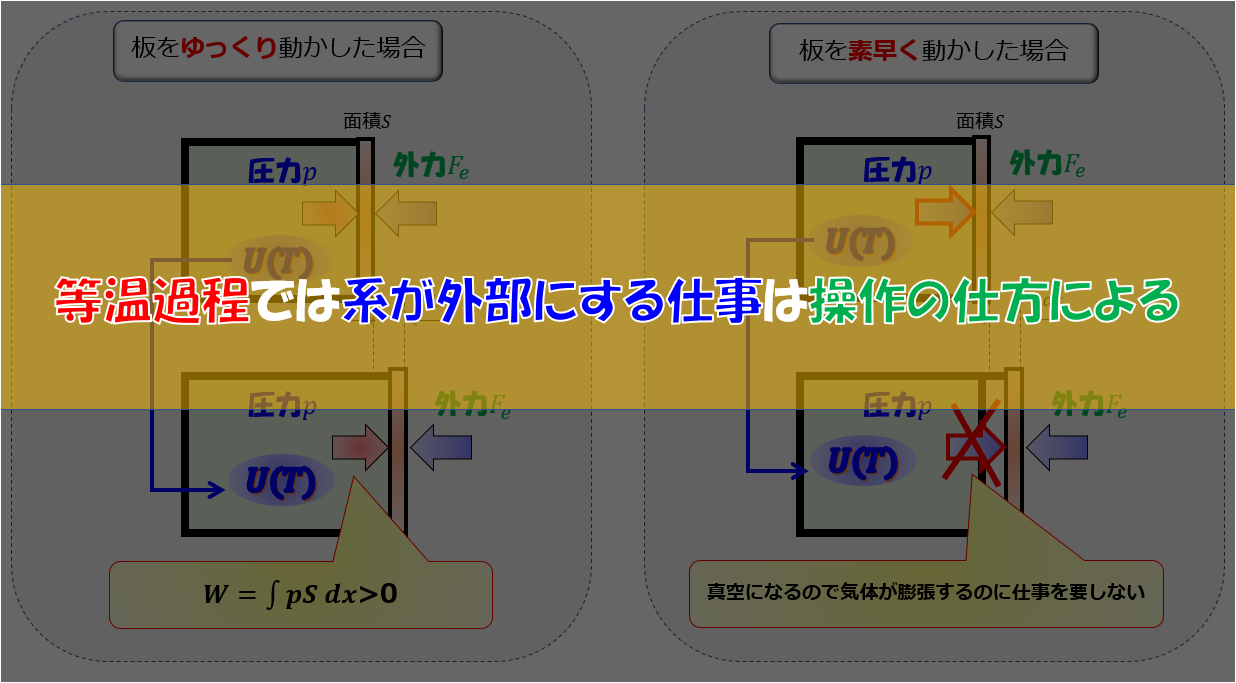
等温過程の場合に、操作の仕方によって系(気体)が外部にする仕事が変わります。
↑こちらが本記事の趣旨です。
まずは状況説明をします。
今から2通りの操作の仕方を考えるのですが、初期状態はどちらも「温度一定下にした状態で、気体\(n\)molが容器に入っている」とします。
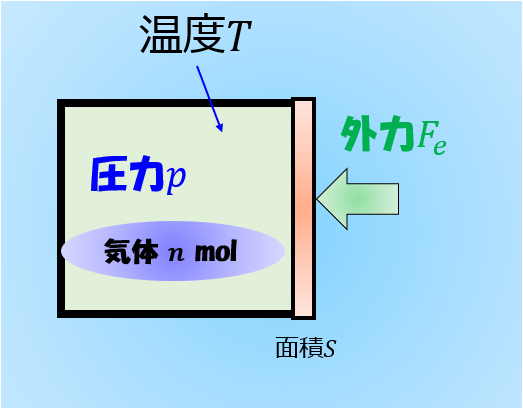

ここで例として、
操作の仕方を次の2通りで考えてみます(‘ω’)ノ
最終状態の体積は両者で同じとして、等温過程なのである決められた温度で最終的に両者落ち着きます。
しかし、この2つの操作によって系(気体)が外部にする仕事が異なる・・・・というのを見ていきます。
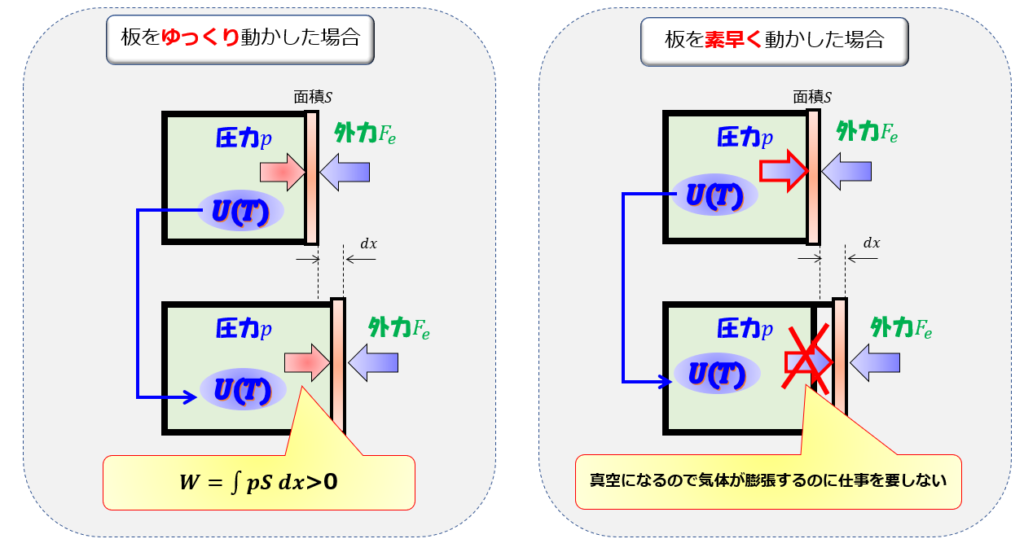
ゆっくり板を引いた場合
ゆ~っくり板を動かしていきます。
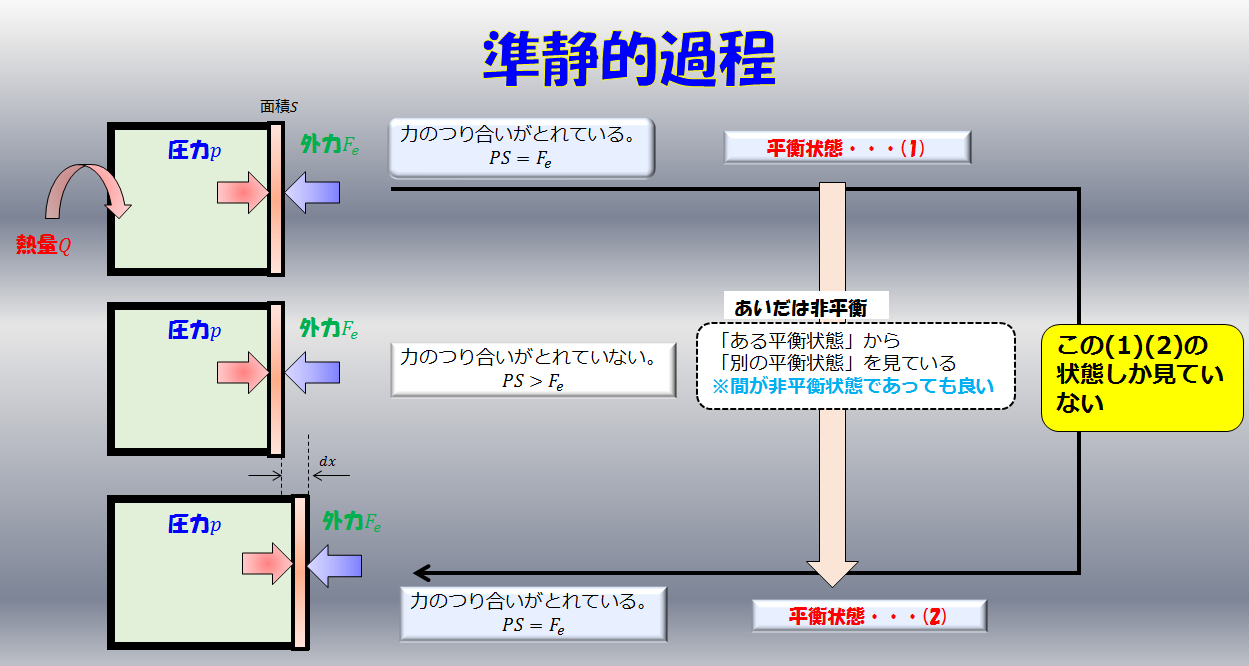
これは準静的等温膨張過程というやつですね。
気体が膨張するときには、外部との力のつり合いが取れた状態で膨張していることになるので、外部の圧力が一定の場合は気体の中の圧力は常に一定になります。
力のつり合いより
pS-F_{e}=0\tag{1}
\end{align*}
系(気体)が外部にする仕事
W=\int pSdx\tag{2}
\end{align*}
系(気体)が外部にする仕事が(2)式となることがわかります。
この(2)式をよく覚えておいてください(‘ω’)ノ
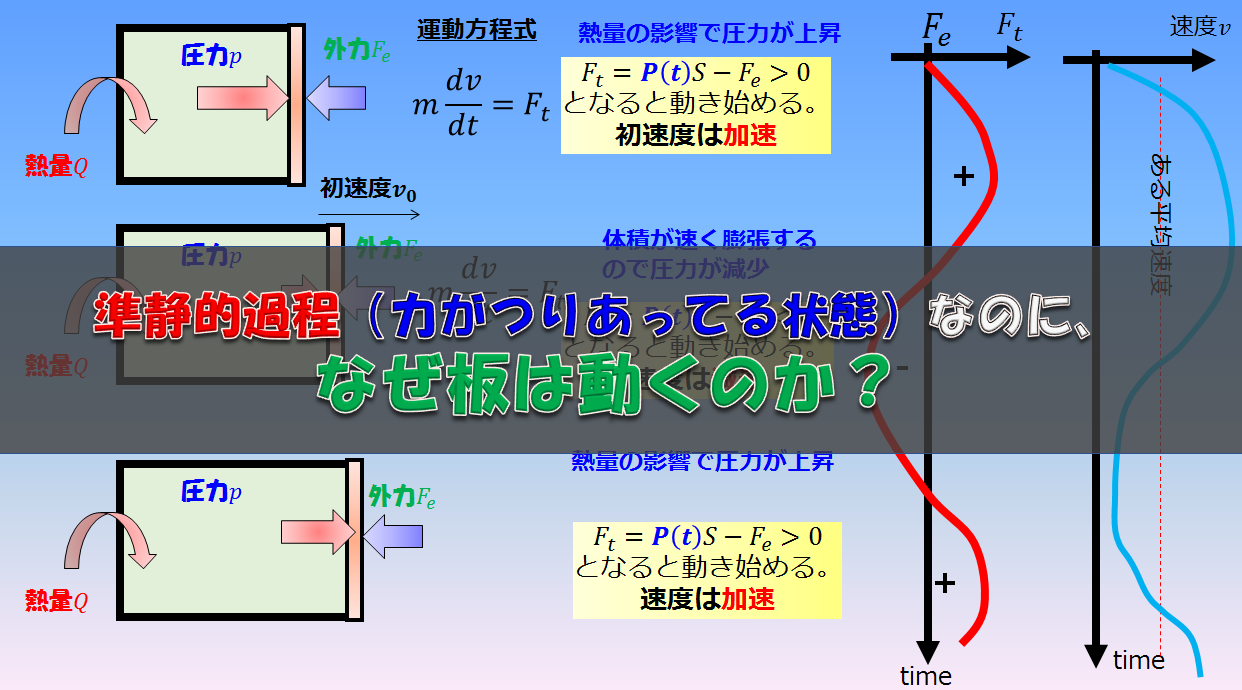
素早く(気体が膨張についていけないくらい)板を引く場合
では素早く引いた場合を考えましょう。
系(気体)が外部にする仕事は(2)式と同じになるでしょうか?
お分かりの通り、(2)式とは異なる結果が得られます。
気体がついてこれないくらい板を素早く引きます。
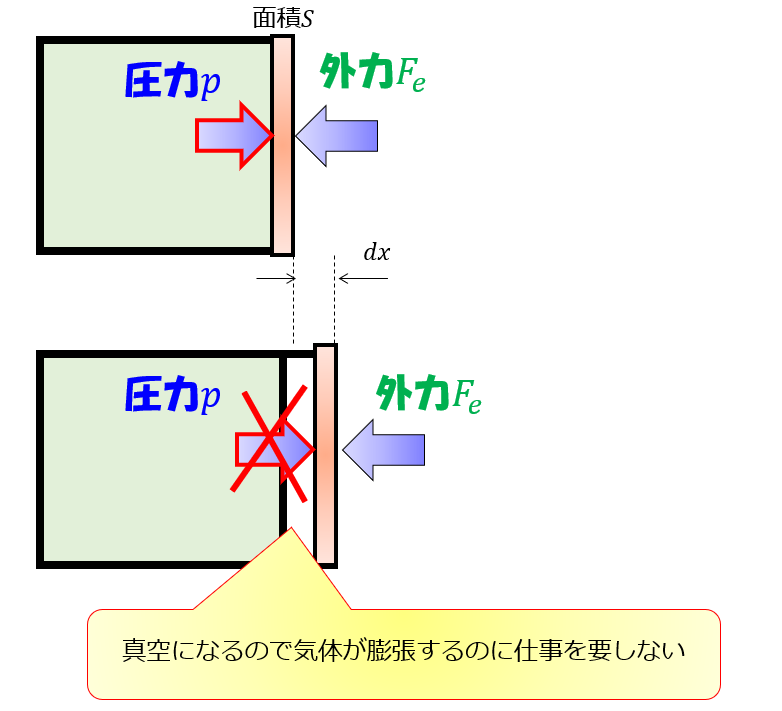

そうすると、板と気体の間に隙間(真空)ができるために、気体が膨張するために阻害する外力というのが無くなります。
ということは、
ラッキー(*’▽’)って感じで楽々と気体は膨張するでしょう!!
つまり、
系(気体)が外部にする仕事は
W=0\tag{3}
\end{align*}
となります。
このように、操作の仕方によって系(気体)が外部にする仕事が異なります。
言い忘れていたことが・・・
板を素早く引いた場合は、気体が膨張するので温度が下がるでしょうし、容器内はとても熱平衡状態とは言えません。
ですから、その状態では圧力や温度は定義できませんが、等温過程であるためやがて決められた温度に落ち着きます。
そうすると、2通りの操作の仕方での「温度が同じ、容器の体積も同じ、気体のモル数も同じ」であるため、熱力学におけるマクロな物理量は両者同じであります。
けれども、操作の仕方によって系(気体)が外部にする仕事は異なるというわけです。

まとめ
本日の記事は、等温過程では系が外部にする仕事は操作の仕方によるというのを示しました。
余談・・・
熱力学は熱平衡状態での学問であるので、素早く引いて間に非平衡な状態を作ると、
熱力学が使えないように思えますが、別に間にどんな非平衡な状態があっても、
最終的に熱平衡状態に落ち着けばその時点での熱力学のマクロな物理量は定義できるので問題がありません。
等温過程の場合は、最終の状態は同じなのに、操作の仕方によって系(気体)が外部にする仕事が異なりましたが・・・断熱過程では?
結果は、下記のような感じです。
| 断熱過程 |
|
熱力学第一法則 \(Q=\Delta U +W\) ※\(W\)は気体が外部にする仕事 ↓ 断熱なので\(Q=0\) ↓ \(\Delta U=-W\) |
| 内部エネルギーは状態量なので、
系が外部にした仕事の過程に依らず、 始点と終点だけの状態量だけで決まる。 |
断熱過程の場合は、最終の状態が同じであれば、間にどんな操作の仕方をしても、系(気体)が外部にする仕事は同じです。
断熱過程の場合については、また次回にしましょう(^^)/