こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本内容は、「比熱の温度依存性の理解のため」のための記事です。
本記事の内容です。
量子論から導かれる調和振動子は、2原子分子の比熱には全く寄与しないというのを見ていきます。
調和振動子の量子化エネルギーは低温極限では、「凍結している状態」とよく表現されています。
「凍結している状態」とは一体どんな状態なのか?
本記事を通して学んで頂ければと思います!
また、実験ではなぜ比熱が常温で\(C=\frac{7}{2}k_B\)ではなく\(C=\frac{5}{2}k_B\)に近い値を取るのかが理解できる内容となります。
量子力学における基礎式であるシュレディンガー方程式を使うことになります(^^)/
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の復習:2原子分子のシュレディンガー方程式
念のために、前回の復習をしておきましょう。
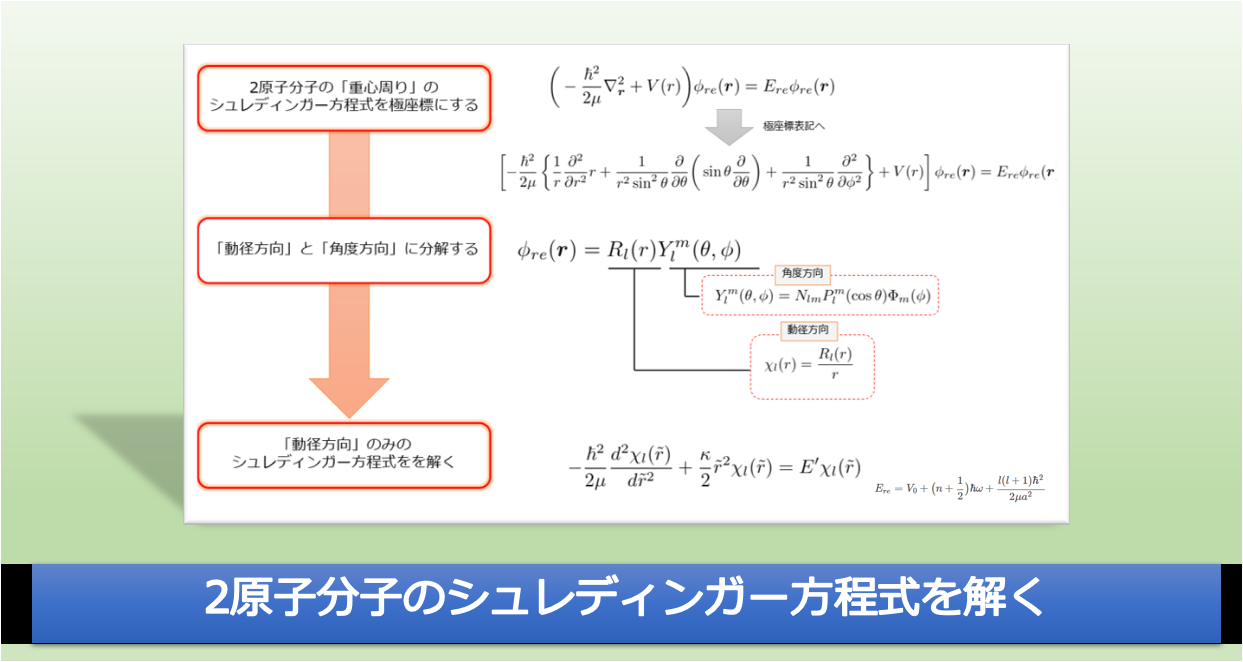
前回は、2原子の分子のシュレディンガー方程式から求めたエネルギー固有値をもとめました。
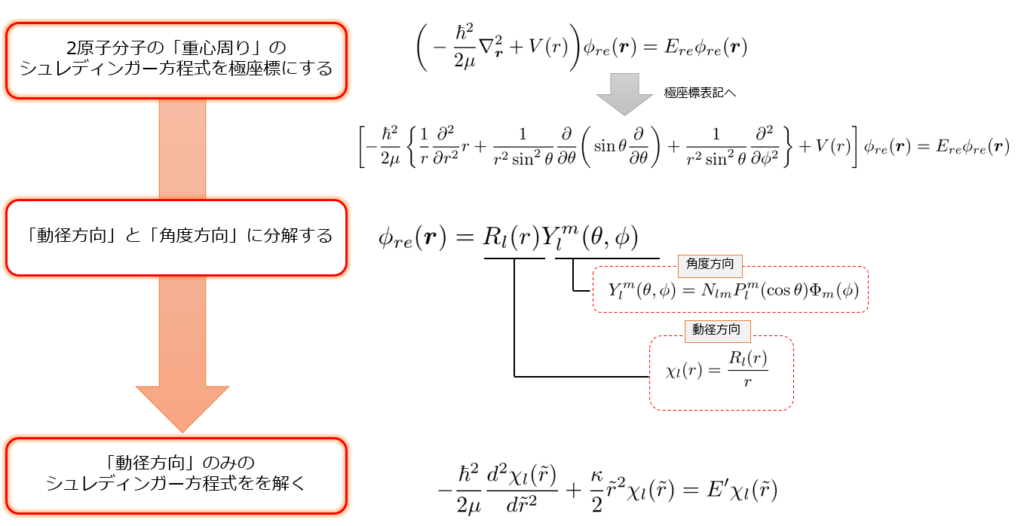
【解き方のフロー】
\left [ -\frac{\hbar^2}{2\mu}
\left \{ \frac{1}{r}\frac{\partial^2 }{\partial r^2}r+\frac{1}{r^2\sin^2\theta}\frac{\partial }{\partial \theta}\bigg(\sin\theta\frac{\partial}{\partial\theta}\bigg)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}\right \} +V(r) \right ]\phi_{re}(\boldsymbol{r})= E_{re}\phi_{re}(\boldsymbol{r})
\end{align*}
のエネルギー固有値は、
E_{re}=V_0+\big(n+\frac{1}{2}\big)\hbar\omega+\frac{l(l+1)\hbar^2}{2\mu a^2}
\end{align*}
エネルギー固有値が求まったら、比熱を計算するまでの流れは定石として以下のように決まっていますので覚えておきましょう。
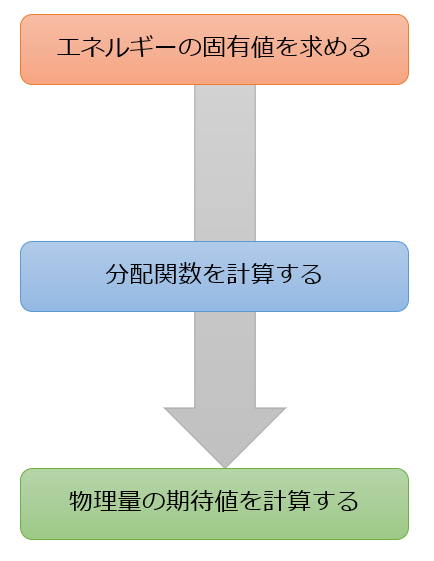
エネルギー固有値がわかれば、分配関数がわかり、色々な物理量(比熱も含む)が求まります。
だから分配関数がとても重要なのですよね(^^)
エネルギー固有値から分配関数を計算する
E_{re}=V_0+\big(n+\frac{1}{2}\big)\hbar\omega+\frac{l(l+1)\hbar^2}{2I}\tag{1}
\end{align*}
※\(I=\mu a^2\):慣性モーメント
分配関数
Z_{re}=\underset{n,l,mについての和}{\underline{\sum}}e^{-\beta E_{re}}\tag{2}
\end{align*}
※\(\beta=\frac{1}{k_B T}\)
(1)式を(2)式に代入します。
Z_{re} &= \sum_{n=0}^{\infty}\sum_{l=0}^{\infty}\sum_{m=-l}^{l}\exp\left \{ -\left [\bigg(n+\frac{1}{2}\hbar\omega\bigg)+\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\\
&=\underset{振動の項(vibration)}{\underline{\sum_{n=0}^{\infty}\exp\left [-\bigg(n+\frac{1}{2}\hbar\omega\bigg)\beta\right ]}}\times \underset{回転の項(rotation)}{\underline{\sum^{\infty}_{l=0}\sum^{l}_{m=-l}\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}}}\\
&=Z_{vib}(\beta)\times Z_{rot}(\beta)\tag{3}
\end{align*}
このように素直に計算して、「振動の項」と「回転の項」に分けることができました。
振動の項(vibration)の分配関数
Z_{vib}(\beta)=\sum_{n=0}^{\infty}\exp\left [-\bigg(n+\frac{1}{2}\hbar\omega\bigg)\beta\right ]\tag{4}
\end{align*}
回転の項(rotation)の分配関数
Z_{rot}(\beta)=\sum^{\infty}_{l=0}\sum^{l}_{m=-l}\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\tag{5}
\end{align*}
比熱は「振動の項」と「回転の項」に分離できる
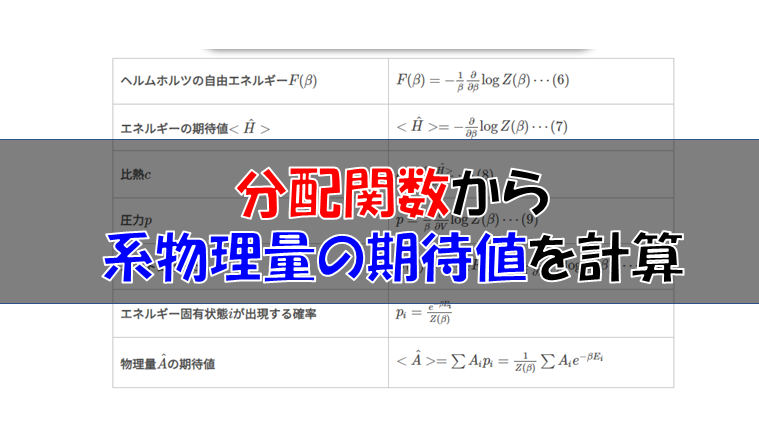
分解関数さえわかれば色々な物理量の期待値が計算できるのでしたよね。
| ヘルムホルツの自由エネルギー\(F(\beta)\) | \(F(\beta)=-\frac{1}{\beta}\log Z(\beta)\cdots (6)\) |
| エネルギーの期待値\(<\hat{H}>\) | \(<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\cdots (7)\) |
| 比熱\(c\) | \(c=\frac{\partial <\hat{H}>}{\partial T}\cdots (8)\) |
| 圧力\(p\) | \(p=-\frac{\partial F}{\partial V}=\frac{1}{\beta}\frac{\partial}{\partial V}\log Z(\beta)\cdots (9)\) |
| エントロピー\(S\) | \(S(\beta)=-\frac{\partial}{\partial T}F(\beta)\cdots (10)\) |
| エネルギー固有状態\(i\)が出現する確率 | \(p_{i}=\frac{e^{-\beta E_{i}}}{Z(\beta)}\) |
| 物理量\(\hat{A}\)の期待値 | \(<\hat{A}>=\sum A_{i}p_{i}=\frac{1}{Z(\beta)}\sum A_{i}e^{-\beta E_{i}}\) |
分配関数を知るとこれだけの物理量が計算できるのですから、とても便利なものだなという印象を持ってもらえたかと思います。
比熱はエネルギーの温度微分なので以下のように書けます。
C_{re}(T)&=\frac{d<\hat{H}>}{dT}\\
&=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{re}(\beta)\\
&=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log\big(Z_{vib}(\beta)+Z_{rot}(\beta)\big)\\
&=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{vib}(\beta)-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{rot}(\beta)\\
&=C_{vib}(T)+C_{rot}(T)\tag{6}
\end{align*}
このように比熱も「振動の項」と「回転の項」に分けることができました。
振動の項(vibration)の比熱
C_{vib}(T)=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{vib}(\beta)\tag{7}
\end{align*}
回転の項(rotation)の比熱
C_{rot}(T)=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{rot}(\beta)\tag{8}
\end{align*}
低温極限、高温極限
(7)(8)式のように手計算で計算が進められれば良いのですが、手計算で進めるのが困難な場合も当然あります。
解析的に理解する方法は以下のように2つあります。
- 数値計算で比熱を求める
- 「低温」もしくは「高温」での極限で考える
数値計算での振る舞いは追々やるとして、ここではできるだけ手計算で理解できるように「低温 or 高温」での極限を考えて考察を進めることにします。
ここで、低温・高温という表現には注意が必要ですね。
何℃以下なら低温などという考え方をしてはいけません。
何に対して低温なのかを考える必要があります。
振動の項
分配関数の指数部分を見ると、温度が効いてくるのは\(\hbar\omega\beta=\frac{\hbar\omega}{k_{B} T}\)があります。
つまり、
- \(\hbar\omega>>k_{B} T\):低温極限
- \(\hbar\omega<<k_{B} T\):高温極限
と考えることで、温度の極限に対する比熱の振る舞いを考察することができます。
回転の項
分配関数の指数部分を見ると、温度が効いてくるのは\(\frac{\hbar^2}{2I}\beta=\frac{\hbar^2/2I}{k_{B} T}\)があります。
つまり、
- \(\hbar^2/2I>>k_{B} T\):低温極限
- \(\hbar^2/2I<<k_{B} T\):高温極限
と考えることで、温度の極限に対する比熱の振る舞いを考察することができます。
振動の項の比熱を求める
まずは、「振動の項」の分配関数から比熱を計算しましょう。
振動の項(vibration)の分配関数
Z_{vib}(\beta)&=\sum_{n=0}^{\infty}\exp\left [-\bigg(n+\frac{1}{2}\hbar\omega\bigg)\beta\right ]\\
&=\frac{\exp\big(-\beta\hbar\omega/2\big)}{1-\exp\big(-\beta\hbar\omega\big)}\tag{9}
\end{align*}
初項\(\exp\big(-\beta\hbar\omega/2\big)\)、公比\(\exp\big(-\beta\hbar\omega\big)\)の無限等比級数の公式を使いました。
これで分配関数が計算できましたので、次に比熱を計算します。
振動の項(vibration)の比熱
C_{vib}(T)=-\frac{d}{dT}\frac{\partial }{\partial \beta}\log Z_{vib}(\beta)\tag{10}
\end{align*}
比熱は(10)式のように計算できるので、まずは分配関数のlogをとって\(\beta\)で微分します。
ちょっと丁寧に計算していきます。
まずは、\(\log Z_{vib}(\beta)\)の\(\log\)から・・・
\log Z_{vib}(\beta)=\log e^{-\frac{\hbar\omega}{2}\beta}-\log\big(1-e^{-\hbar\omega\beta}\big)
\end{align*}
次に、\(\beta\)で微分します。
\frac{\partial }{\partial\beta}\log Z_{vib}(\beta) &=-\frac{\hbar\omega}{2}-\frac{e^{-\hbar\omega\beta}\hbar\omega}{1-e^{-\hbar\omega\beta}}\\
&=-\hbar\omega\bigg(\frac{1}{2}+\frac{1}{e^{\hbar\omega/k_{B} T}}\bigg)
\end{align*}
よって、エネルギーの期待値を計算すると、
<H_{vib}>&=-\frac{\partial}{\partial \beta}\log Z_{vib}(\beta) \\
&=\hbar\omega\bigg(\frac{1}{2}+\frac{1}{e^{\hbar\omega/k_{B} T}-1}\bigg)\tag{11}
\end{align*}
そして、比熱を計算すると、
C_{vib}(T)&=\frac{d<H_{vib}>}{dT}\\
&=\frac{e^{\frac{\hbar\omega}{k_{B} T}}}{\big(e^{\hbar\omega/k_{B} T}-1\big)^2}\frac{\hbar\omega}{k_B T^2}\tag{12}
\end{align*}
では、ここから低温極限と高温極限の比熱の振る舞いを見ていきましょう。
低温極限 \(\hbar\omega>>k_{B} T\)
低温極限を考えると\(\hbar\omega>>k_{B} T\)なのだから、\(e^{\hbar\omega/k_{B} T}>>1\)となります。
なので、エネルギーは、
<H_{vib}>\simeq \hbar\omega\bigg(\frac{1}{2}+e^{-\hbar\omega/k_{B}T} \bigg)\tag{13}
\end{align*}
となります。
比熱を求めるには、エネルギーを温度で微分すればよいですね。
低温極限での比熱は、
C_{vib}(T)&=\frac{d<H_{vib}>}{dT}\\
&=\frac{(\hbar\omega)^2}{k_B T^2}e^{-\hbar\omega/k_{B} T}\tag{14}
\end{align*}
となります。
(14)式だけ見ても低温極限での振る舞いがわかりにくいですが、\(\frac{\hbar\omega}{k_B T}>>1\)という高温極限でエネルギーを近似すると
<H_{vib}>\simeq \frac{\hbar\omega}{2}\tag{15}
\end{align*}
と一定値になります。
これは調和振動子ポテンシャルに閉じ込められた1粒子でのエネルギー固有値\(E_{n}=\big(n+\frac{1}{2}\big)\hbar\omega\)の\(n=0\)、つまり\(E_{0}=\frac{1}{2}\hbar\omega\)の零点振動と同じ振る舞いだということです。
もう少し、詳しく説明します。
比熱についても考えてみましょう。
比熱については、\(\frac{\hbar\omega}{k_B T}\)という条件で以下のように冪の部分は無限大になり指数部分は0に近づきます。


指数部分の方が0に近づくスピードが早いので、低温極限\(\frac{\hbar\omega}{k_B T}\)では比熱は0となります。
比熱が0というのはとても重要な結論です。
↓比熱についての記事はこちらをどうぞ。
もう少し説明を加えると、分子には多くの内部運動(分子の振動、回転・・・・・もっとミクロな視点では電子や原子核の回転運動など)が考えられます。
本来は、それらの運動全てが比熱に寄与します。
しかし、低温極限の振動運動において「比熱が0⇔温度上昇に対して全くエネルギーを必要としない」という理論的な結論は、言わば最低エネルギー状態でじっとしていることを意味しているのです。
この状態を、参考書では「凍結している状態」と表現されています。
凍結している状態の意味がわかりずらいかもしれませんね。絵で書くと以下のようになります。
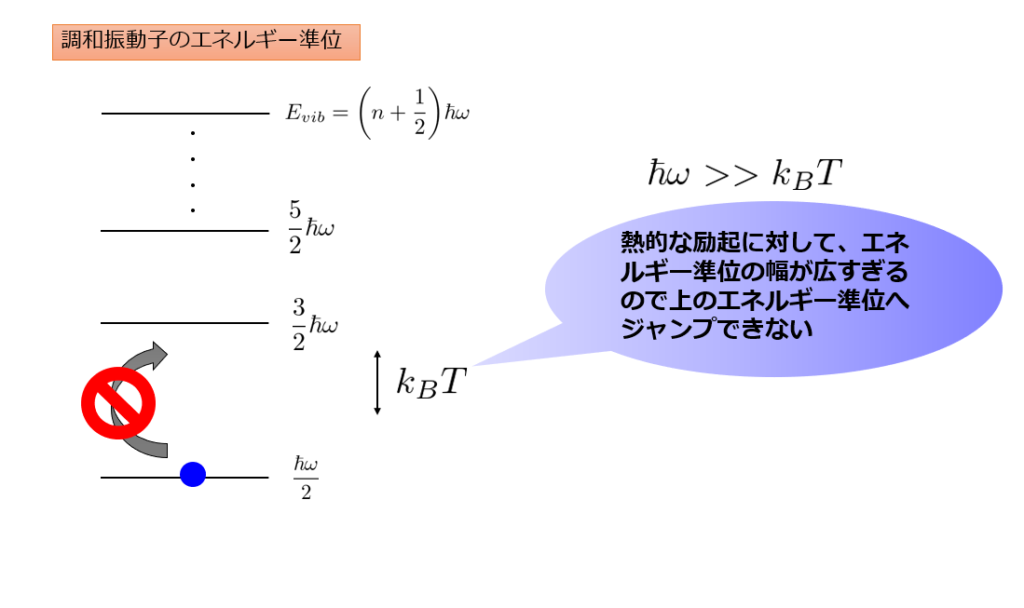

低温極限で「凍結している状態」というのは、熱的励起(熱的なエネルギー\(k_B T\))に対して振動運動は最低エネルギー状態でじっとしている状態のことをイメージすればよいのかなと思います・・・
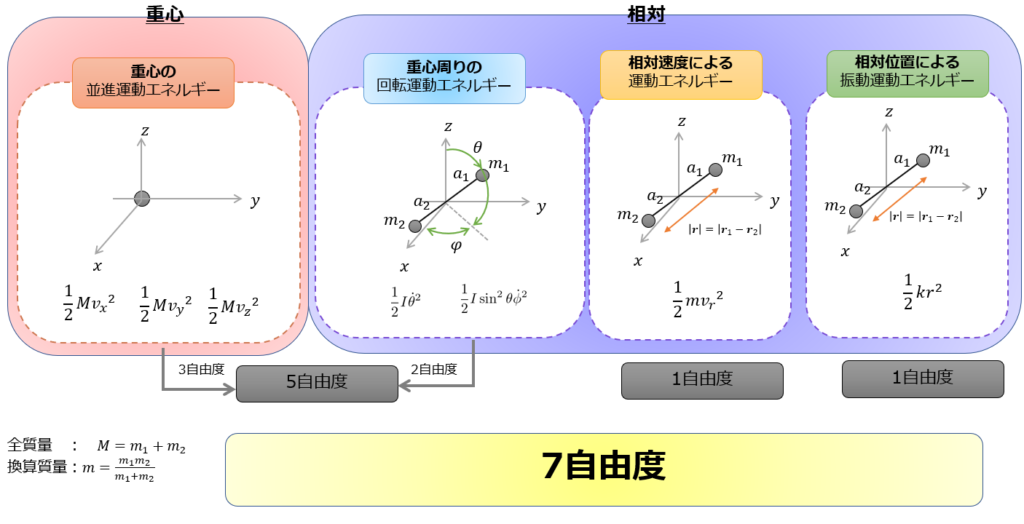
だから、もし振動の項が比熱に寄与していないのであれば、2原子分子の低温極限で比熱に寄与する運動状態は、
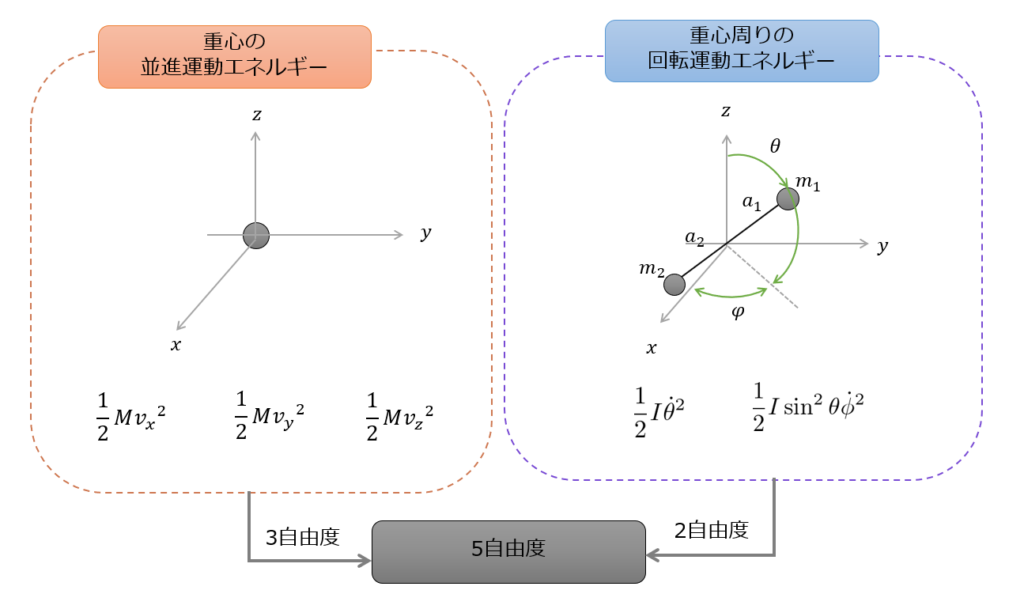
- 重心運動の3自由度
- 回転運動の2自由度
合計5自由度だけということになります。(回転運動についてははまだ議論していませんが・・・・)
振動の項が比熱に寄与していないという結論には至っていませんが、仮説では上記の事が言えるわけですね。
高温極限 \(\hbar\omega<<k_{B} T\)
高温状態を考えると\(\hbar\omega<<k_{B} T\)なのだから、\(e^{\hbar\omega/k_{B} T}\)をテーラー展開の1次の項まで展開しましょう。
e^{\hbar\omega/k_{B} T}\simeq 1+\frac{\hbar\omega}{k_B T}
\end{align*}
と近似して話を進めましょう。
エネルギーはどうなるのかというと、
<H_{vib}>&\simeq \hbar\omega\bigg(\frac{1}{2}+\frac{1}{1+\hbar\omega/k_B T-1}\bigg)\\
& =\frac{\hbar\omega}{2}+k_B T\\
& =k_B T\bigg(\frac{1}{2}\frac{\hbar\omega}{k_B T}+1\bigg)\\
& \simeq k_B T\tag{16}
\end{align*}
となります。
比熱を求めるには、エネルギーを温度で微分すればよいです。
高温極限での比熱は、
C_{vib}(T)=k_{B}\tag{13}
\end{align*}
と一定値になります。
古典近似で十分扱えるような状態(高温極限)においては、自由度が\(f\)の場合の比熱は\(C_{vib}=\frac{f}{2}k_B\)となることは前回の記事で書きました。
これはハミルトニアンが\(H=\frac{p^2}{2m}+\frac{1}{2}\kappa x^2\)という、運動量の2乗と位置の2乗からなるので、自由度が2だから比熱が\(C_{vib}(T)=k_{B}\)となったことと矛盾しない結果となりました。
もう少し意味を考えてみましょう。
比熱とは、「1kg(もしくは1mol)の物質を1K上昇させるのに必要なエネルギー」と定義されており、その値が一定値をとっているということは、エネルギーを加えたら加えた分だけ温度上昇するということです。
これを絵に書くと、低温極限ではエネルギー準位がとびとびに見えていたものが、高温極限ではエネルギー準位が熱的な励起(\(k_B T\))に対してとびとび具合が見えなくなります。
即ちエネルギー準位が連続的に見えるということです。
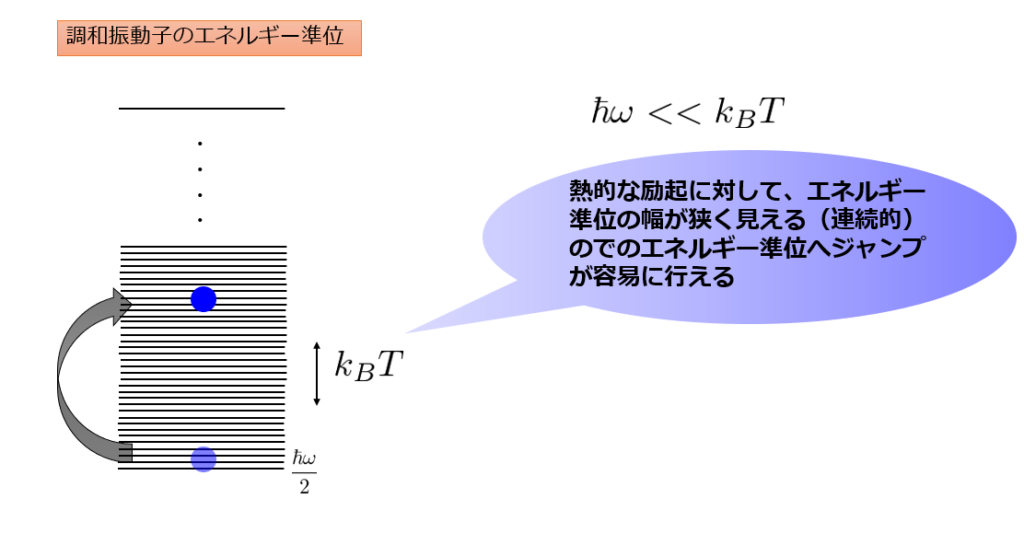

以上からも、
- 量子力学的効果を考えるのであればエネルギー準位が飛び飛びになる(低温極限)
- 古典力学ではエネルギーは連続的に扱える(高温極限)
と表現されるのが理解できたと思います(^^)/
言い換えると、
- 低温極限では量子力学で扱う必要がある
- 高温極限では古典力学で扱っても良い
となります。
回転の項の比熱を求める
「回転の項」も振動の項と同様の方法で分配関数から比熱を求めるわけですが、回転の項は素直に計算できる状態にはありません。
ひとまず分配関数を見てみましょう。
回転の項(rotation)の分配関数
Z_{rot}(\beta)=\sum^{\infty}_{l=0}\sum^{l}_{m=-l}\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\tag{5}
\end{align*}
和の中が\(m\)についての和がないので、
Z_{rot}(\beta)=\sum^{\infty}_{l=0}(2l+1)\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\tag{18}
\end{align*}
↑ひとまずここまでできます。
低温極限 \(\hbar^2/2I>>k_{B} T\)
低温極限からやっていきましょう(^^)/
まずは、分配関数(18)式の\(\sum\)を展開します。
回転の項(rotation)の分配関数
Z_{rot}(\beta)&=\sum^{\infty}_{l=0}(2l+1)\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\\
&=1+3e^{-\beta\hbar^2/I}+5e^{-3\beta\hbar^2/I}+7e^{-6\beta\hbar^2/I}+\cdots+\\
&=1+3e^{-\beta\hbar^2/I}\bigg(1+\frac{5}{3}e^{-2\beta\hbar^2/I}+\frac{7}{3}e^{-3\beta\hbar^2/I}+\cdots +\bigg)\tag{19}
\end{align*}
で、結局\(\hbar^2/2I>>k_{B}T\)(低温極限)をするのですから、初めの2項しか残りませんね。
Z_{rot}(\beta)\simeq 1+3e^{-\beta\hbar^2/I}
\end{align*}
これで低温極限での分配関数が求まりました。
では、エネルギーの期待値を求めましょう。
<H_{rot}>&=-\frac{\partial}{\partial \beta}\log Z_{vib}(\beta) \\
&=\frac{3\hbar^2 e^{-\frac{\beta\hbar^2}{I}}}{I\big(1+e^{-\beta\hbar^2/I}\big)}\\
& \underset{\hbar^2/2I>>k_{B}T}{\underline{\rightarrow}} \frac{3\hbar^2}{I}e^{-\frac{\beta\hbar^2}{I}}\tag{20}
\end{align*}
そして、比熱は、
C_{rot}(T)&=\frac{d<H_{rot}>}{dT}\\
&=\frac{3\hbar^4}{I^2k_{B} T^2}e^{-\frac{\hbar^2}{Ik_{B} T}}\tag{21}
\end{align*}
これが低温極限での比熱の振る舞いです(‘ω’)ノ
高温極限 \(\hbar^2/2I<<k_B T\)
続いて高温極限をやっていきましょう(^^)/
まずは、分配関数(5)式を少し分解しましょう。
回転の項(rotation)の分配関数
Z_{rot}(\beta)&=\sum^{\infty}_{l=0}(2l+1)\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\\
&=\sum^{\infty}_{l=0}2l e^{ -l^2\hbar^2 \beta/2I}e^{ -l\hbar^2 \beta/2I}\\
&+\sum^{\infty}_{l=0}e^{ -l^2\hbar^2 \beta/2I}e^{ -l\hbar^2 \beta/2I}\tag{22}
\end{align*}
ここで、\(x^2=\frac{\beta l^2\hbar^2}{I}\)とおくと、
Z_{rot}(\beta)&=\sum^{\infty}_{l=0}2l e^{ -l^2\hbar^2 \beta/2I}e^{ -l\hbar^2 \beta/2I}\\
&=2\sum_{\Delta x}\sqrt{\frac{I}{\beta\hbar^2}}\Delta x\sqrt{\frac{I}{\beta\hbar^2}} e^{-\frac{x^2}{2}}\\
&=\frac{2I}{\beta\hbar^2}\int_{0}^{\infty}x e^{-\frac{x^2}{2}}\\
&=\frac{2I}{\hbar^2}\beta^{-\beta}\tag{23}
\end{align*}
では、エネルギーの期待値を求めましょう。
<H_{rot}>&=-\frac{\partial}{\partial \beta}\log Z_{vib}(\beta) \\
&=k_B T\tag{24}
\end{align*}
そして、比熱は、
C_{rot}(T)&=\frac{d<H_{rot}>}{dT}\\
&=k_B\tag{25}
\end{align*}
これが高温極限での比熱の振る舞いです(‘ω’)ノ
まとめ
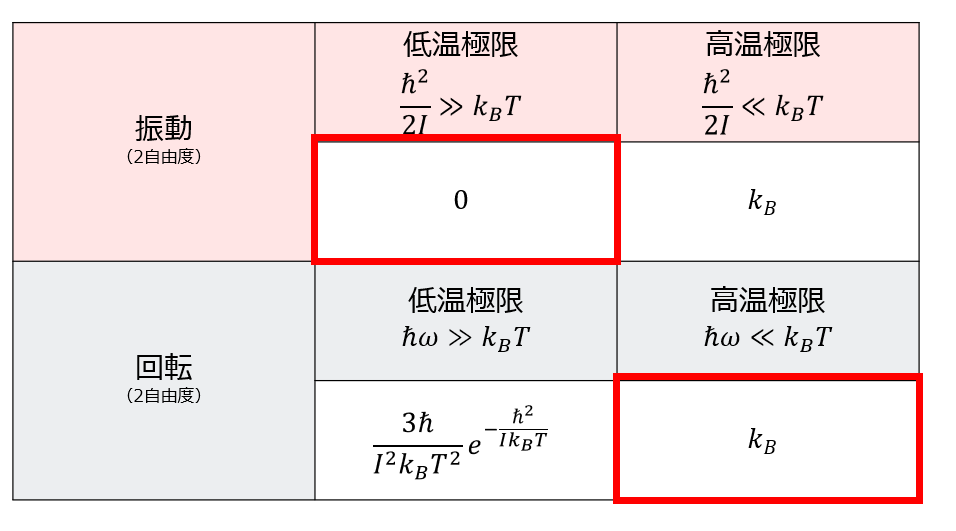
今までの結果をまとめると以下となります。
2原子分子における「振動の項」と「回転の項」の分配関数は以下のようにわかっています。
振動の項(vibration)の分配関数
Z_{vib}(\beta)=\sum_{n=0}^{\infty}\exp\left [-\bigg(n+\frac{1}{2}\hbar\omega\bigg)\beta\right ]\tag{4}
\end{align*}
回転の項(rotation)の分配関数
Z_{rot}(\beta)=\sum^{\infty}_{l=0}\sum^{l}_{m=-l}\exp\left \{ -\left [\frac{l(l+1)\hbar^2}{2I} \right ] \beta\right \}\tag{5}
\end{align*}
しかし、手計算では計算を進めることができないので、低温極限と高温極限に分けて比熱を求めました。
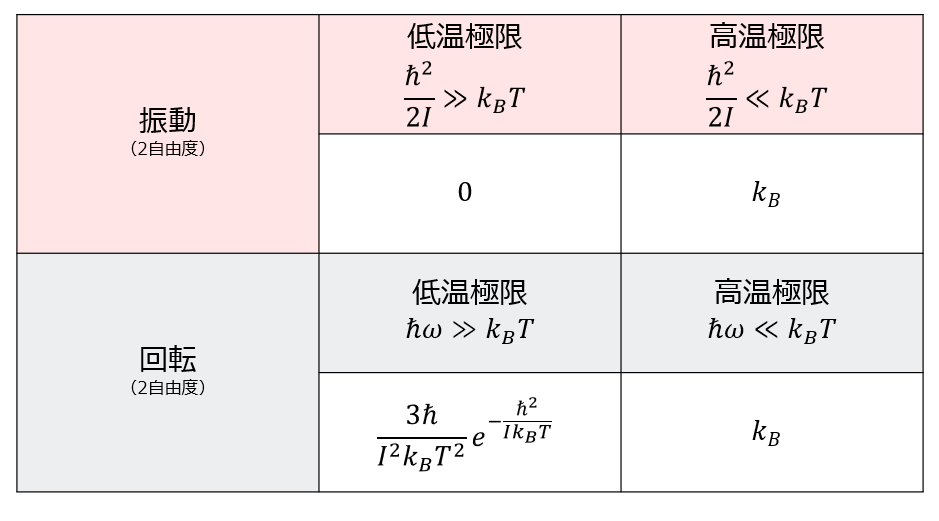
振動の項
- \(\hbar\omega>>k_{B} T\):低温極限
- \(\hbar\omega<<k_{B} T\):高温極限
回転の項
- \(\hbar^2/2I>>k_{B} T\):低温極限
- \(\hbar^2/2I<<k_{B} T\):高温極限
ということは、常温(20℃くらい)でどちらの極限をとっているのかは、実験値から計算してみなければわかりません。
では、もし「振動の項」も「回転の項」も、どちらも高温極限で考えた場合はどうなるのかというと・・・
高温極限で考えるということは、量子的効果(エネルギーがとびとびな不連続な値をとる)が見えず、古典近似での振る舞いとなるので・・・・
古典近似における2原子分子の比熱
C=\frac{7}{2} k_B
\end{align*}
となります。
※本記事ではしつこく言っていることですが、この「2原子分子の比熱」\(c=\frac{7}{2} k_B\)は実験値とは一致しません。
以下の2点が実験事実です。
- 2原子分子の比熱は\(\frac{5}{2}k_B T\)に近い
- 比熱は温度の広い範囲で一定値であるが、温度依存性を持っている
この2点を解消するためには、「振動の項から来る量子化エネルギーは凍結していて比熱に寄与していないのではないか」という仮説が立ちます。
だから実は常温では、比熱に寄与する運動の自由度は5自由度が主に担っているのではないかという仮説です。
ということは、常温では本当に以下の条件が満たされているのかを計算してみれば良いですね。
上記の条件が成り立つのであれば、常温での比熱は、
- 重心運動の3自由度
- 回転運動の2自由度
からの熱的励起によるエネルギーだけが寄与しており、2原子分子の比熱は\(\frac{5}{2}k_B T\)に近い
という結論が導かれます。
本当に、
振動の項
- \(\hbar\omega>>k_{B} T\):低温極限
回転の項
- \(\hbar^2/2I<<k_{B} T\):高温極限
なのかは次回の記事で考えたいと思います(/・ω・)/