どうも(^^)/
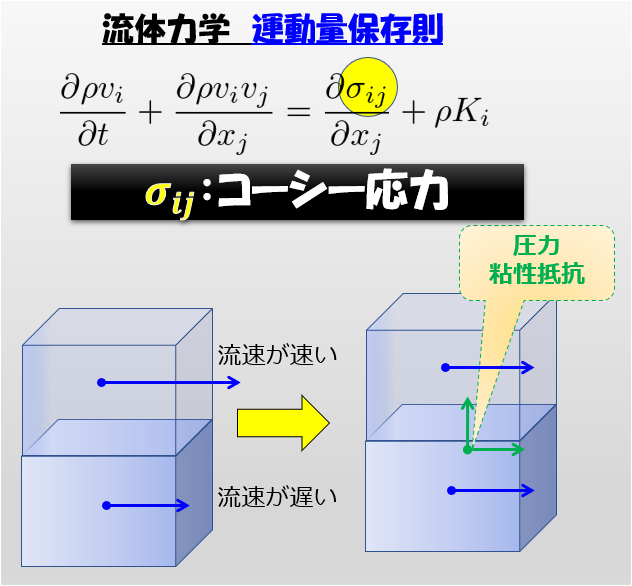
流体力学において渦が発生する、あるいは乱流が発生するなどはとてもメジャーな内容でしょう。
でも、めちゃくちゃ疑問です。。。
渦が生成する例などはいくらでもありますよね。
例えば、円柱まわりの流れ場では円柱の背後に渦を生成します。

- なぜ渦が生成されるのか?
- 渦を生成する要因は何か?
当ブログ内で”渦が生成するためのヒント”をいくつか与えられたらなと思います。
※完全なメカニズムまでは説明しきれないですが。
渦が生成するための仕組みを理解するために、以下の内容を順番に投稿していきたいと思います。
- 流体力学の循環の定義←本記事の内容
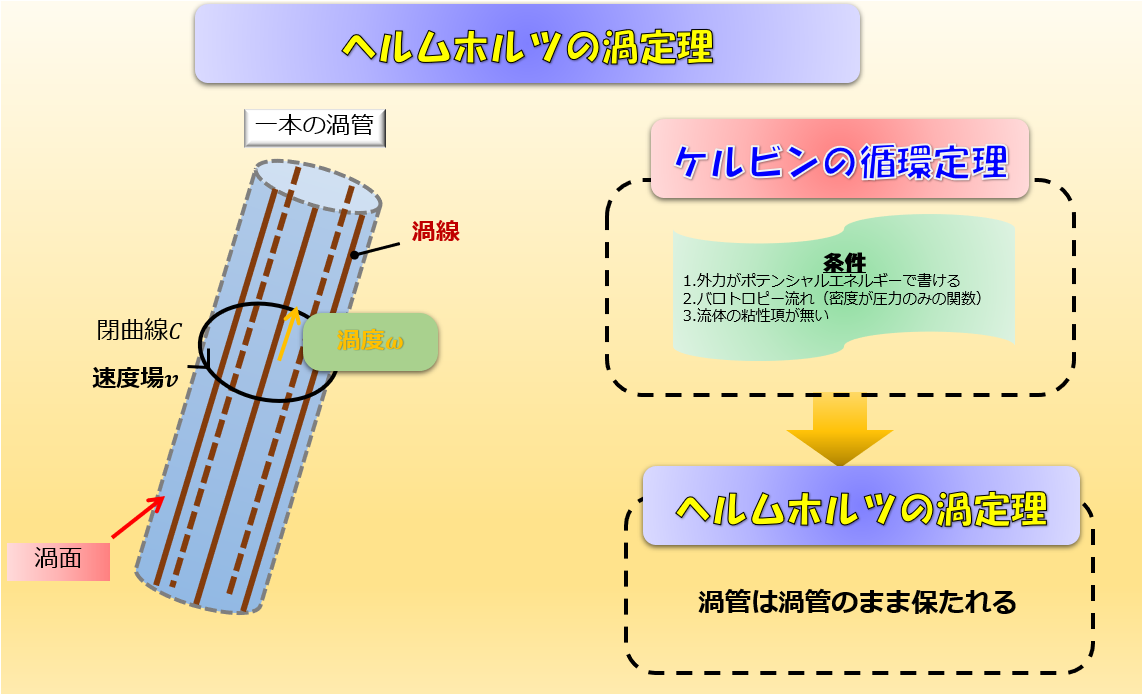
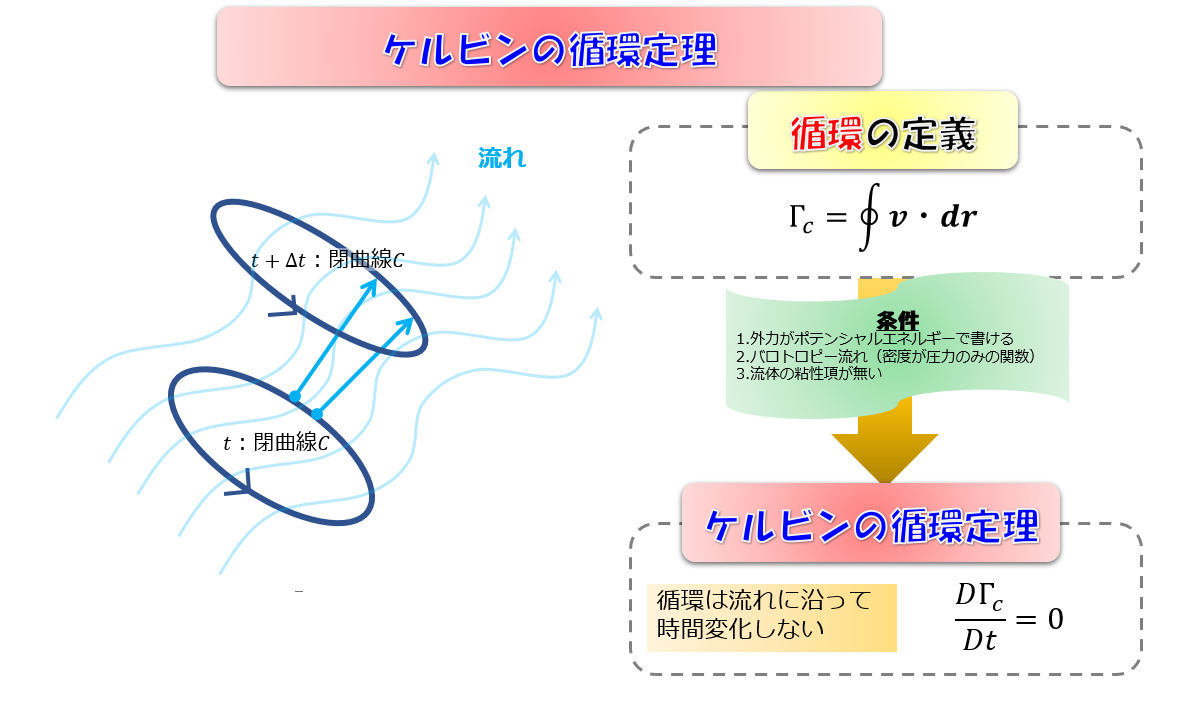
- ケルビンの循環定理
- ヘルムホルツの渦定理
- ラグランジュの渦定理
- ケルビンの循環定理を破る例(量子流体を例にする)
では、本記事の内容は流体力学の循環の定義という内容をやっていこうと思います(^^)/
流体力学の循環の定義
循環の定義は以下のように定義します。
流れ場があるところに、閉曲線\(C\)を適当に描くことにします。
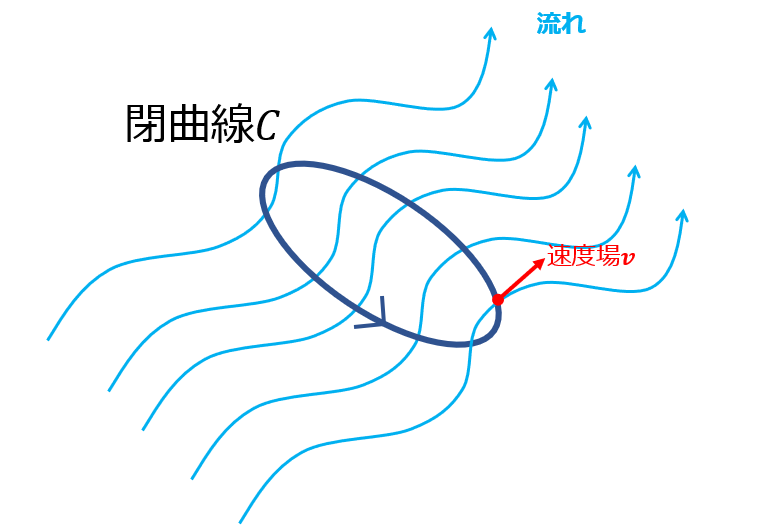

その閉曲線に沿って、流速の速度場で一周線積分します。
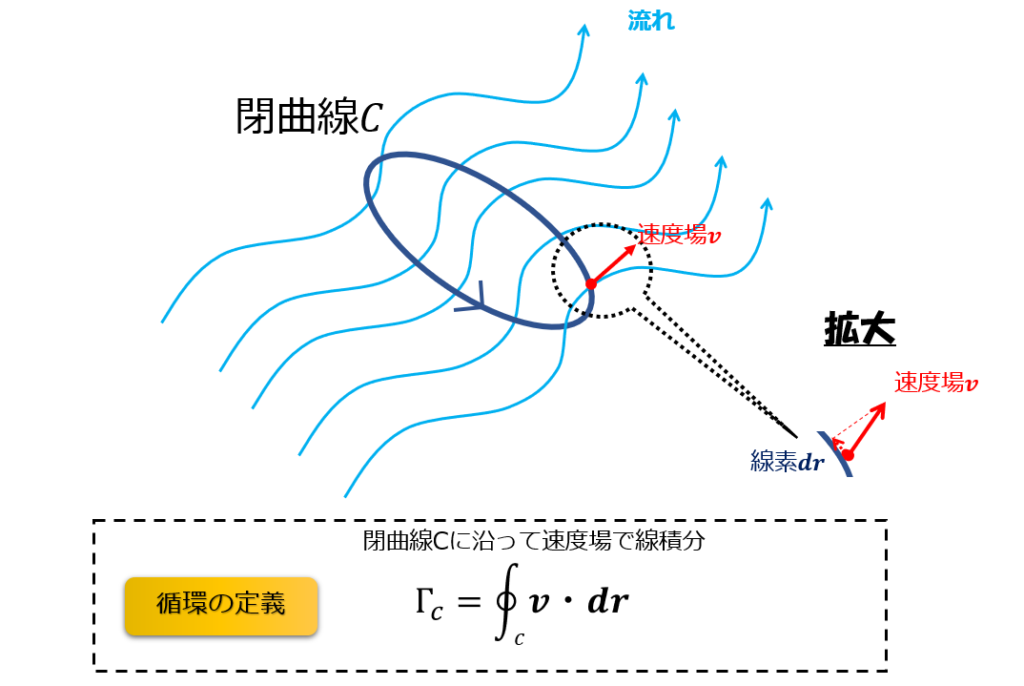

このように、流れがあるところに閉曲線\(C\)を適当に作り、流速の速度場で一周線積分したものを循環と言います。
循環の定義
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{1}
\end{align*}
これが循環の定義です(^^)/
循環の意味は?
循環の定義を示しましたが、一体これがどんな意味を持っているのかを説明します。
循環の定義は以下でした。
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{1}
\end{align*}
まず、これを見てあれをやりたくなる人もいるでしょう。
あれとは・・・・ストークスの定理です。
ストークスの定理は、電磁気学のアンペールの法則でもよく使います。
公式を以下に示しておきます。
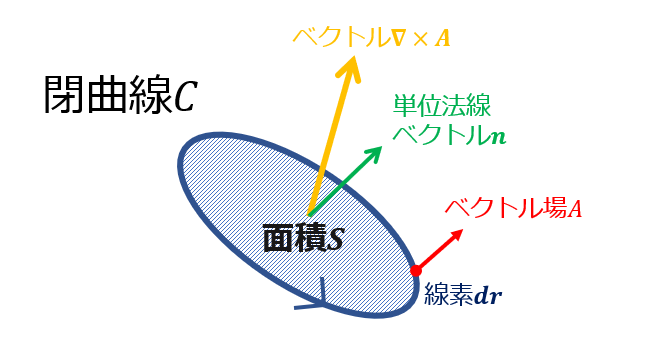

\Gamma_{c}=\oint_{c} \boldsymbol{A} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{A} \bigg)\cdot\boldsymbol{n}dS\tag{2}
\end{align*}
線積分していたものが、閉曲線で閉じられた面積とそれに垂直なベクトルとの掛け算・・・のような感じで表現できるというわけです。
この公式を循環の定義にも当てはめてみましょう。
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}=\iint_{S}\bigg(\nabla\times \boldsymbol{v} \bigg)\cdot\boldsymbol{n}dS\tag{3}
\end{align*}
とこうなります。
ここで、\(\nabla\times\boldsymbol{v}=\boldsymbol{\omega}\)が渦度\(\boldsymbol{\omega}\)の定義なので、
循環は渦度を使って、
\Gamma_{c}=\iint_{S}\boldsymbol{\omega}\cdot\boldsymbol{n}dS\tag{4}
\end{align*}
となります。
これをマンガちっくに書くと・・・
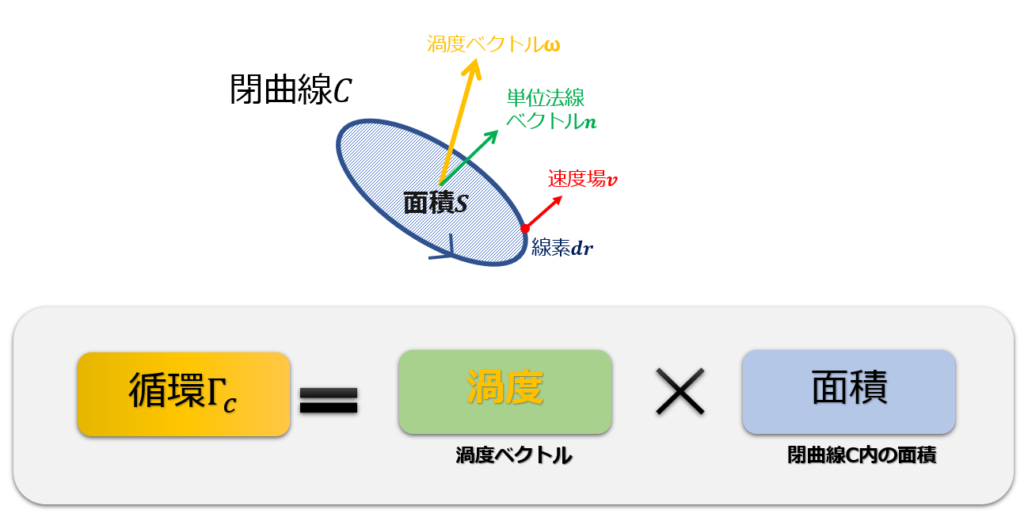

こんな感じです。
循環は、「渦度」と「閉曲線で囲まれた面積」との掛け算ということになります。
同じ面積でも、渦度ベクトルが大きな値を持っていると、循環は大きくなります。
なので、循環は渦度の強さを表現している量であるとも見ることができます。
まとめ
本記事の内容は、渦が生成するためのいくらかのヒントを与えられたらなという思いで書き始めました。
少なくともその理解のためには、循環というものを考えることで有益な情報を得ることができるます。
よって、今回は流れがあるところに閉曲線\(C\)を適当に作り、流速の速度場で一周線積分したもの(循環)というものを定義しました。
循環の定義
\Gamma_{c}=\oint_{c} \boldsymbol{v} \cdot d\boldsymbol{r}\tag{1}
\end{align*}
これが循環の定義です(^^)/
- 流体力学の循環の定義←本記事の内容
- ケルビンの循環定理←次回の内容
- ヘルムホルツの渦定理
- ラグランジュの渦定理
- ケルビンの循環定理を破る例(量子流体を例にする)
では、次回はケルビンの循環定理という内容をやっていこうと思います(^^)/
補足:線積分とは?となったらこれでイメージしておこう
1周線積分がよくわからない人のための補足説明です。
1周線積分ではなくて、イメージしやすいように、閉曲線を開いて直線だと思いましょう。
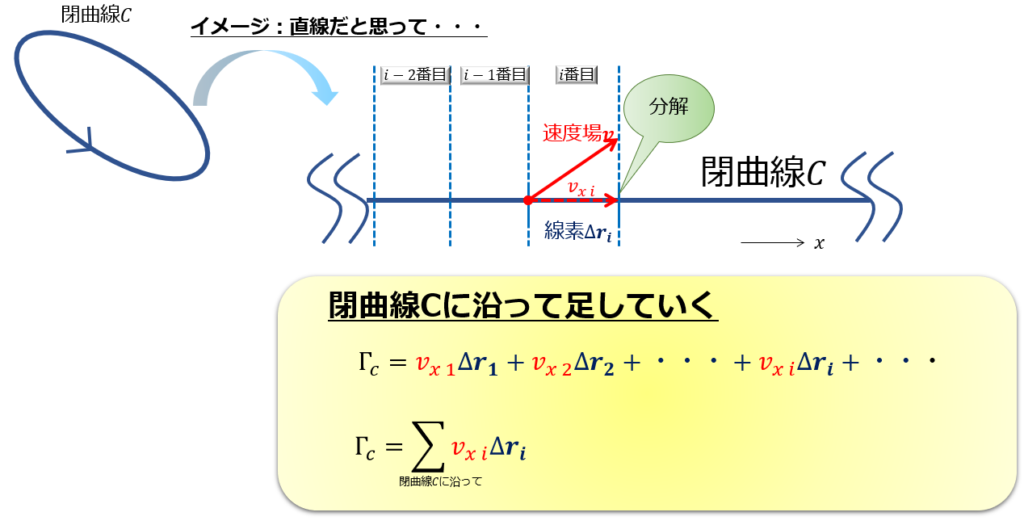

そうすると、区間ごとに速度場と線要素との内積を取っているのがイメージできると思います(^^)/
流体力学を深く理解するための参考書
初心者から中級者で流体力学を学ぶのにおすすめの参考書を以下に列挙しておきます。
流体力学は、「工学向け」か「理学向け」で内容が結構変わってきます。
工学部向け流体力学
工学向けでは以下の3冊をお勧めします。
👆こちらは、初心者でもわかりやすく理解できると思います。
演習書としては以下のものが、難しすぎず・・・がっつり練習できます。
工学部であれば圧縮性の流体まで、学ぶことが多いと思いますので、「圧縮性流体」の参考書としては以下の書籍がお勧めです。
理学部向け流体力学
僕は、理学部出身なので主に愛用していた書籍を紹介します。
👆こちらの書籍は流体力学を学ぶために一番最初に購入した本なのですが、今まで読んだ流体力学の中で一番わかりやすいと思っています。
ただ、残念過ぎるのは「前編」だけを書いて著者がお亡くなったため、「後編」がないという参考書です。それなのに絶版にならずに書籍で見かけるんですから、相当有名なんだろうなと思います。
もう少し優しい参考書としては「今井氏」の流体力学がお勧めですね。
※最後に「1000ページ」くらいの乱流力学の教科書も紹介しておきます(笑)
買ってしまった。。。https://t.co/RPaZNZ3cxv
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) May 16, 2020