こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事の内容はこちら
本記事では1次元の移流方程式を数値計算で解いた時、空間微分を以下の3パターンで解いてみたいと思います。
- 前進差分(1次精度)で解く
- 後退差分(1次精度)で解く
- 中心差分(2次精度)で解く
果たしてどれがまともな数値解を得られるのか・・・
1次元の移流方程式
\begin{align*}\frac{\partial T(x,t)}{\partial t}+u\frac{\partial T(x,t)}{\partial x}=0\tag{1}\end{align*}
数値計算にはFortranを使います。
グラフのアニメーションはgnuplotを使います。
一刻も早く結果を確認したい人は「まとめ」へGo!!
※プログラムのzipファイルがあります。
1次元の移流方程式とは何か
1次元の移流方程式
\begin{align*}\frac{\partial T(x,t)}{\partial t}+u\frac{\partial T(x,t)}{\partial x}=0\tag{1}\end{align*}
※\(u\):一定速度
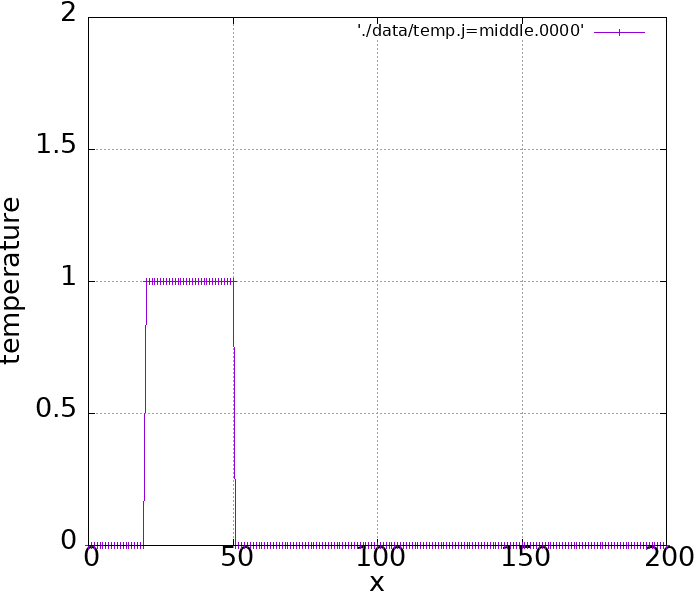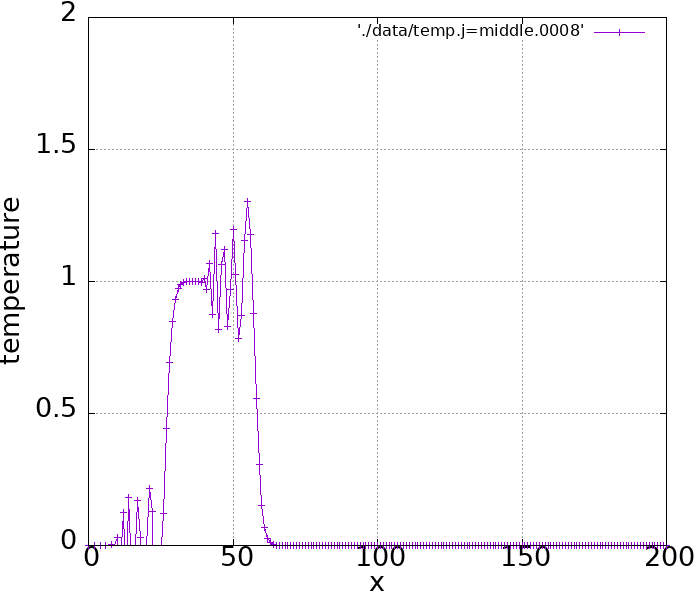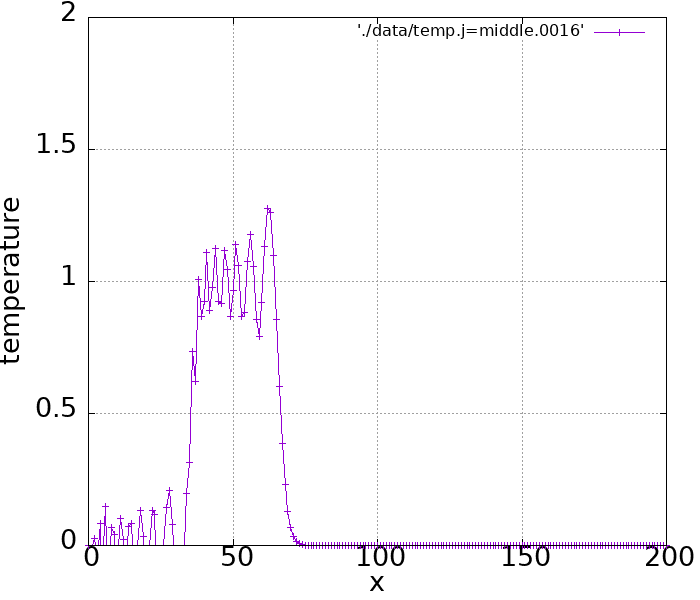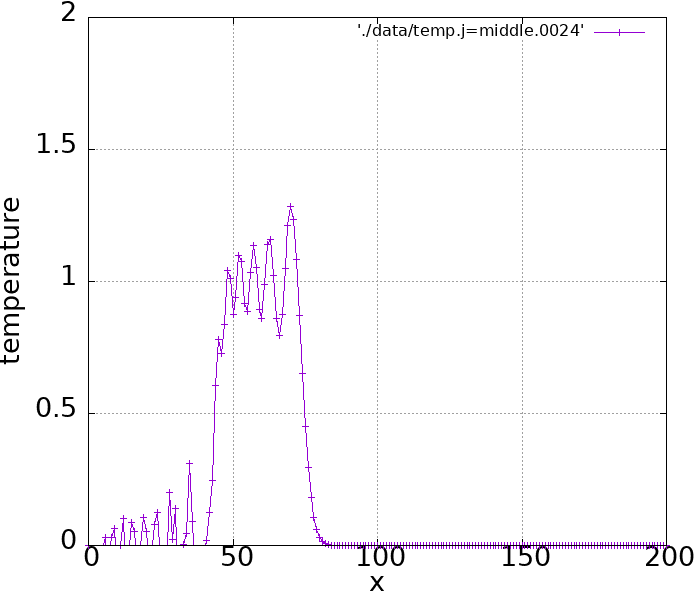
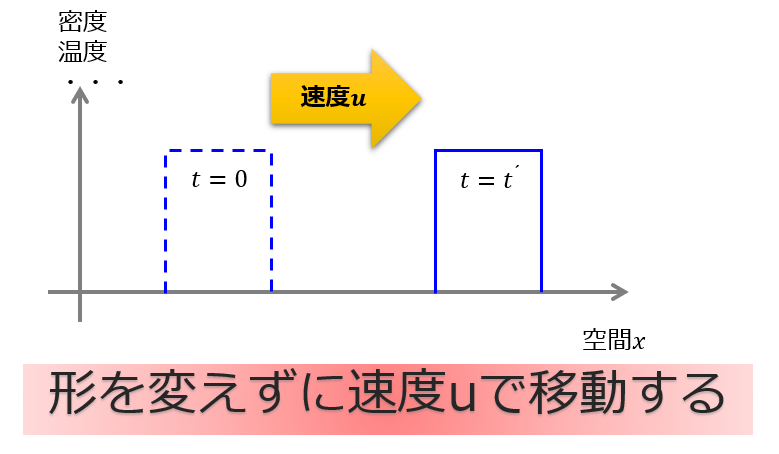
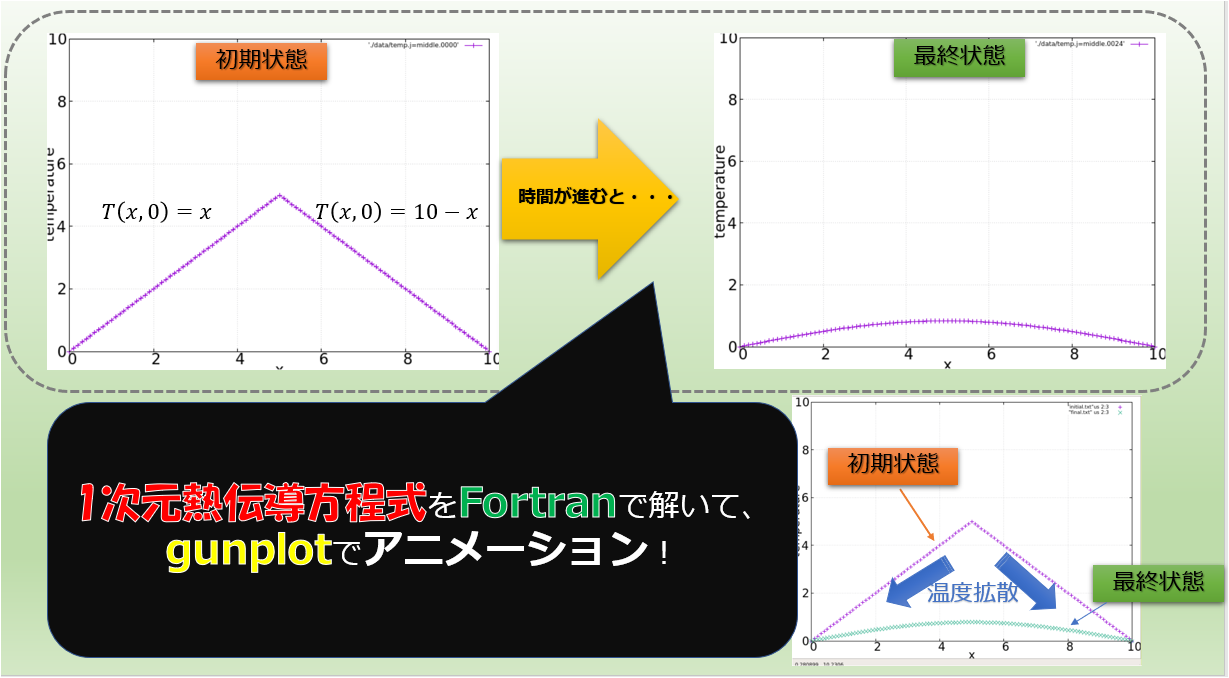
1次元の移流方程式は、下記の絵のように何かの物理量を形を変えずに一定速度\(u\)で運ぶ方程式を意味しています。
横軸は空間\(x\)ですが、縦軸は「密度」や「温度」だったり色々考えることができます。
本記事では、温度\(T\)として扱うことにします。
この移流方程式は、
\begin{align*}\frac{D }{D t}=\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}\tag{2}\end{align*}
とすることで、物質微分を表していることがわかります。
つまり、流れ(流速\(u\))に沿ってどのように物理量が運ばれるかを表している偏微分方程式です。
(1)式を、
\begin{align*}\frac{D T(x,t)}{D t}=0\tag{3}\end{align*}
と表現することもできるので、「なるほど、温度分布が流れに沿って形を変えずに運ばれるのかー」っていうのが見えてくるわけです。
もっと実用的な偏微分方程式の中でこのような移流方程式が出てくるのは、流体の基礎方程式ですかね(‘ω’)
例えば、1次元移流方程式を密度の方程式と考えるならば、
\begin{align*}\frac{D \rho(x,t)}{D t}=0\end{align*}
となります。
これは、「流れに沿って密度が変化しない」・・・・つまり、流体の非圧縮性仮定というなります。
1次元の移流方程式の一般解
1次元の移流方程式は解析解が存在します。
解析解がどのような形になっているかを知っていることで、この後数値計算したときの結果の正しさを評価することができます。
1次元の移流方程式の一般解はとっても簡単です。
以下が(1)式の一般解となります。
もし、速度\(u\)が正なら
\begin{align*}T(x,t)=f(x-ut)\tag{4}\end{align*}
速度\(u\)で右へ進む解
もし、速度\(u\)が負なら
\begin{align*}T(x,t)=g(x+ut)\tag{5}\end{align*}
速度\(u\)で左へ進む解
今回は、速度\(u>0\)としているので(4)式の形が1次元の移流方程式の解であります。
本当かな?と思ったら(4)式を(1)式に代入してみよう
(4)式を(1)式に代入して左辺が0になることを確認してみます。
\begin{align*}\frac{\partial T}{\partial (x-ut)}(-u)+u\frac{\partial T}{\partial (x-ut)}=0\tag{6}\end{align*}
やっぱり0になりましたね(^^)/
1次元の移流方程式をFortranで解く
1次元の移流方程式の厳密解がどのような振る舞いをするのかを理解しました。
1次元の移流方程式:「物理量の分布(形)を変えずに速度\(u\)で運ぶ」
これをFortranを使って数値計算をしてみたいと思います(^^)/
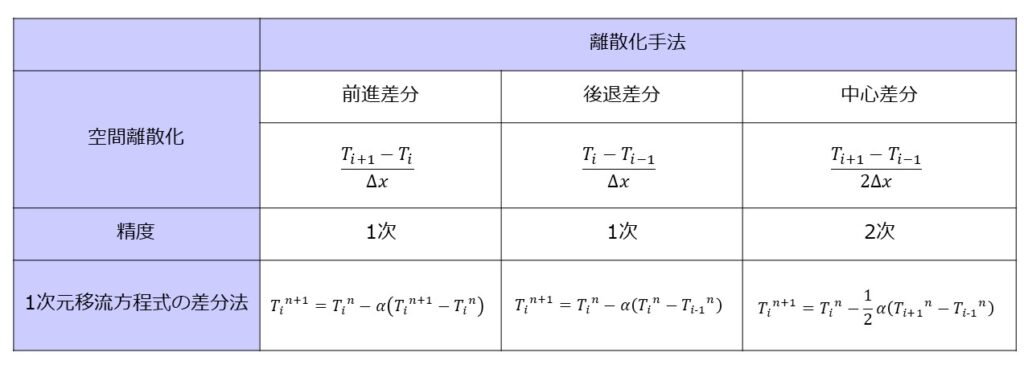
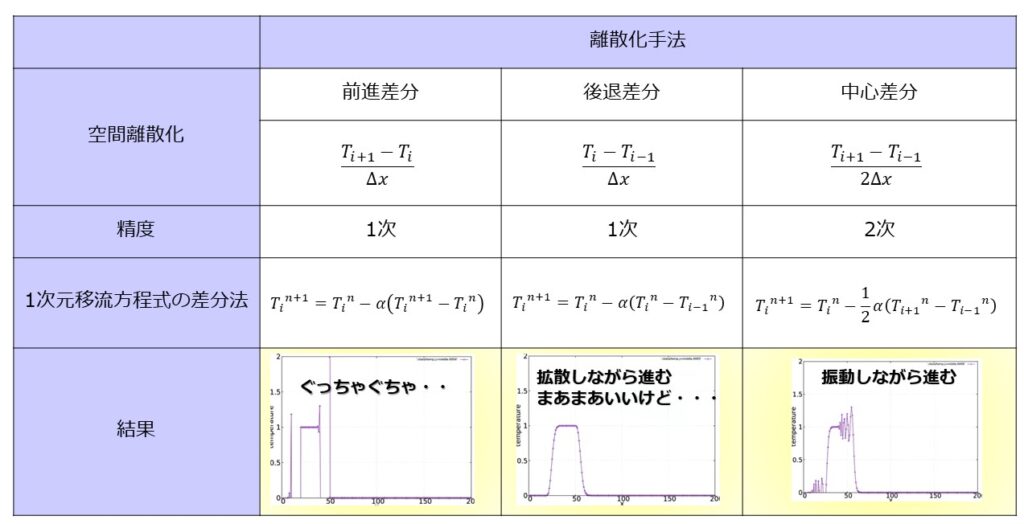
実施する数値計算の空間差分は以下の3パターンです。
プログラムの全体は以下です。(例:前進差分)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
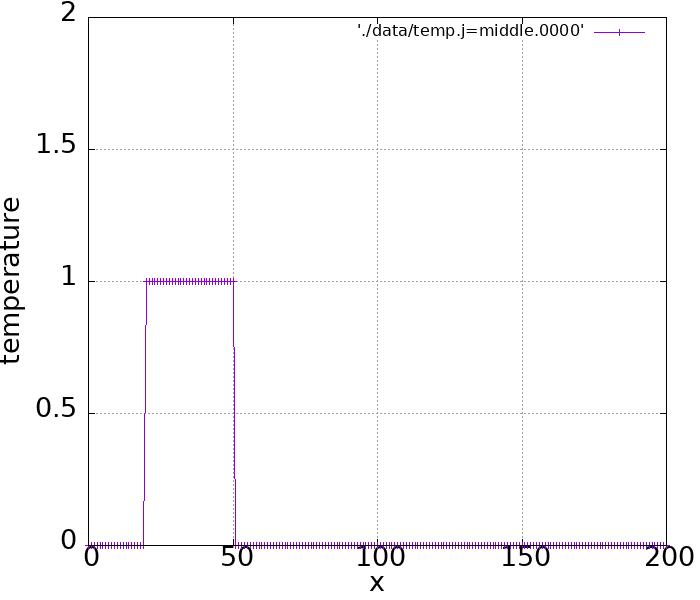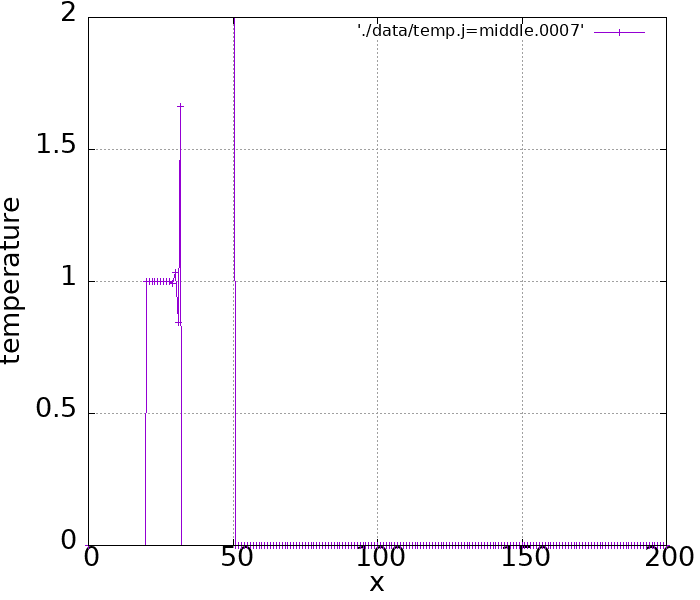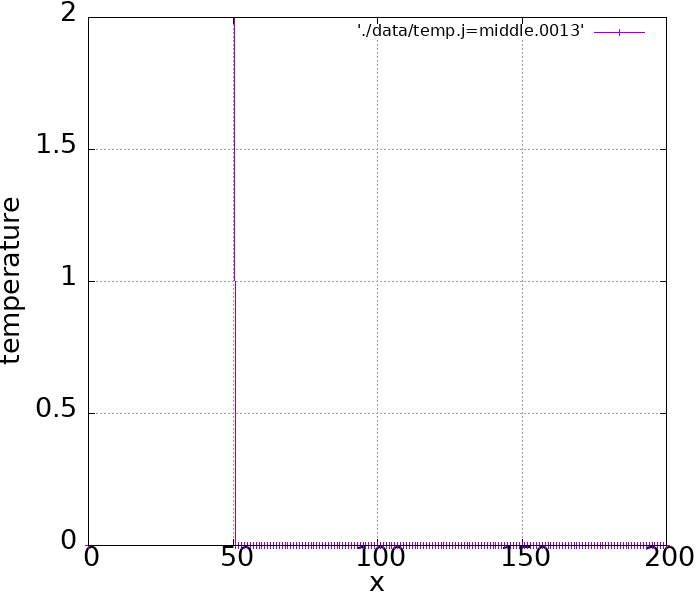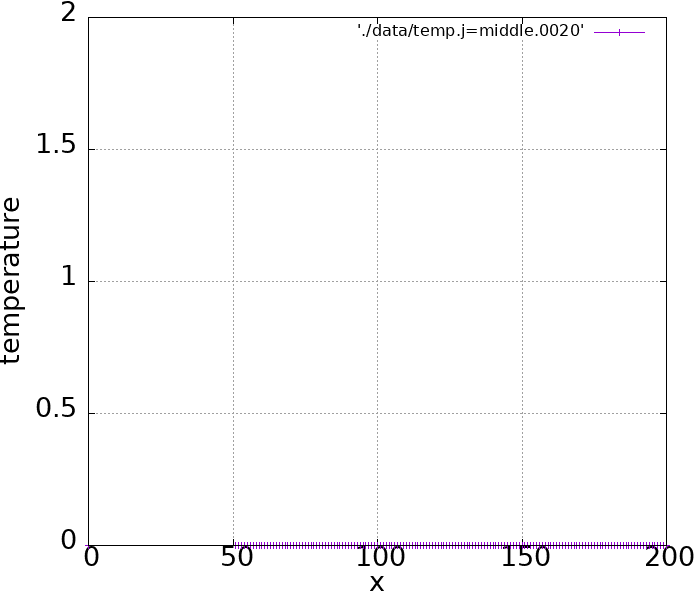
module constants implicit none integer::i,nt integer, parameter :: imax = 200,ntmax = 250 real(8):: T(0:imax),xmax,x,u,dx,dt,cfl integer,parameter :: SP = kind(1.0) integer,parameter :: DP = selected_real_kind(2*precision(1.0_SP)) end module constants module print use constants implicit none contains subroutine print__profile(f) real(DP), dimension(0:imax), intent(in) :: f integer :: counter = 0 character(len=*), parameter :: base = "./data/temp.j=middle." character(len=4) :: serial_num character(len=40) filename write(serial_num,'(i4.4)') counter write(filename,"(a,i5.5,a)") base//serial_num open(10,file=filename) do i = 0 , imax write(10,*) i*dx, f(i) end do close(10) counter = counter + 1 end subroutine print__profile end module print program thermal_explicit use constants use print implicit none u=1 dt = 0.1 xmax = 200 dx = xmax/imax cfl=u*dt/dx open(10,file="initial.txt") open(11,file="final.txt") !initial state do i = 0, imax x = dx*i if (i>=20 .and. i<=50) then T(i) = 1 else T(i) =0 endif write(10,*) i,x,T(i) enddo call print__profile(T(:)) !Time step do nt = 1, ntmax do i = 1, imax-1 T(i) = T(i) -cfl*(T(i+1)-T(i)) end do if (mod(nt,10)==0) call print__profile(T(:)) write(*,*)nt end do !Final state do i = 0, imax x = dx*i write(11,*) i,x,T(i) end do end program thermal_explicit |
もし、後退差分や中心差分で試したい場合は、以下の行を変更するだけです。
グラフのアニメーションはgnuplotを使っています。
実行方法は以下の記事に書いてありますし、本記事の最後にも書いてあります。
前進差分

\begin{align*}\frac{T^{n+1}_{i}-T^{n}_{i}}{\Delta t}+u\frac{T^{n}_{i+1}-T^{n}_{i}}{\Delta x}=0\end{align*}
なので、\(\alpha=\frac{u\Delta t}{\Delta x}>0\)と置くと、
\begin{align*}T^{n+1}_{i}=T^{n}_{i}-\alpha\bigg(T^{n}_{i+1}-T^{n}_{i}\bigg)\tag{7}\end{align*}
となり、(7)式を数値計算で解くことになります。
これをもう少し式変形変形すると、
\begin{align*}T^{n+1}_{i}=(1+\alpha)T^{n}_{i}-\alpha T^{n}_{i+1}\tag{8}\end{align*}
これを数値計算で解くと、以下のようにある位置\(i\)では\(n\)ステップ目の値\(T^{n}_{i}\)が正の値であったとしても、\(n+1\)ステップ目の値\(T^{n+1}_{i}\)は負の値を取ることになります。
そして、\(T^{n+1}_{i}\)(負の値)を使って次のステップ\(T^{n+2}_{i}\)を求めるので、より大きく負の値に振り切れたり、場合によっては正の値をとったり・・・・・振動するという変な数値解が得られることが予想されます。
つまり、全然安定に解けていないということです。
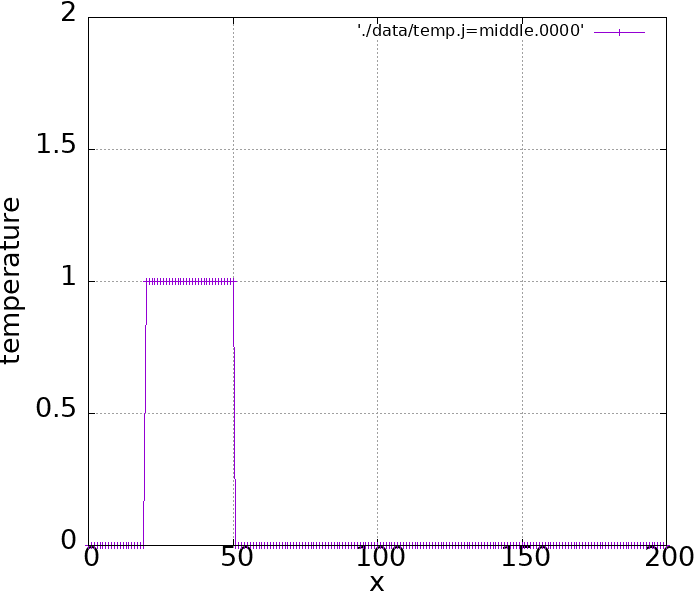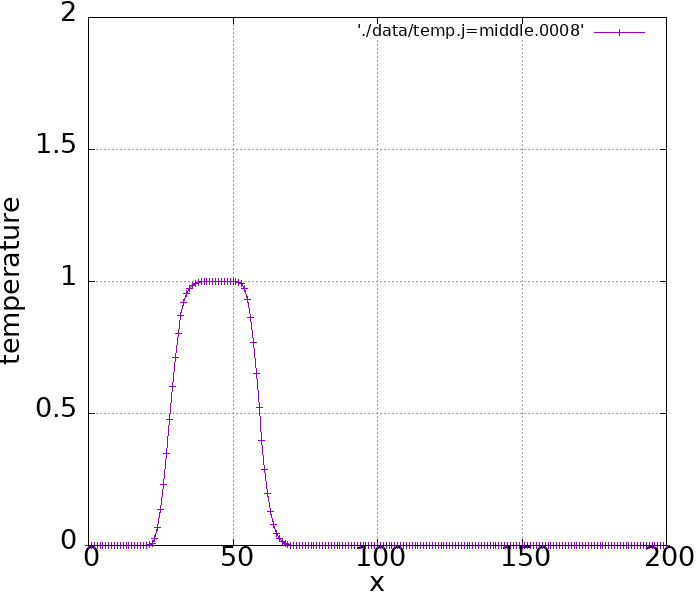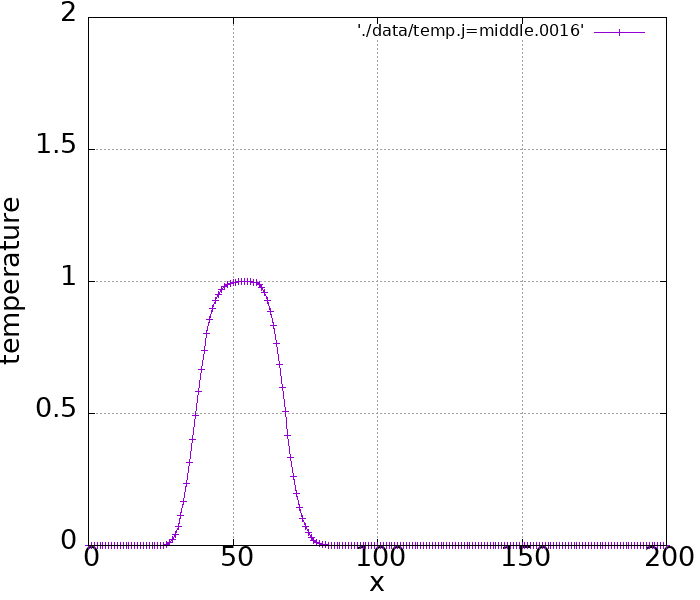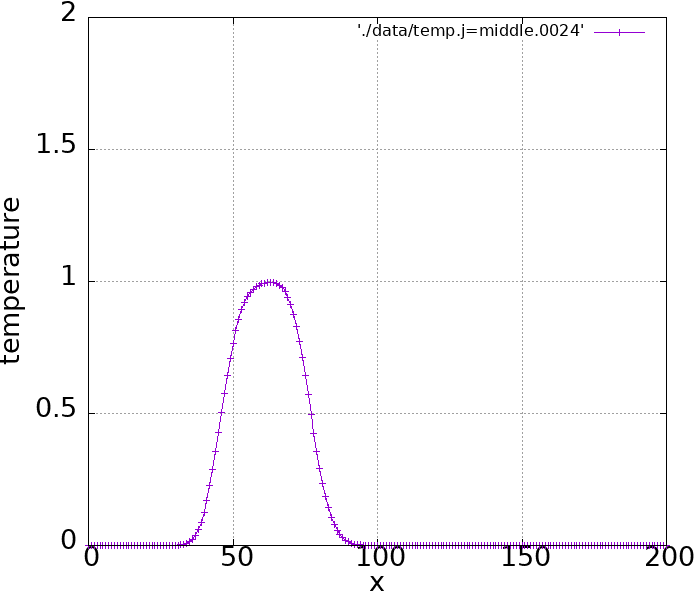
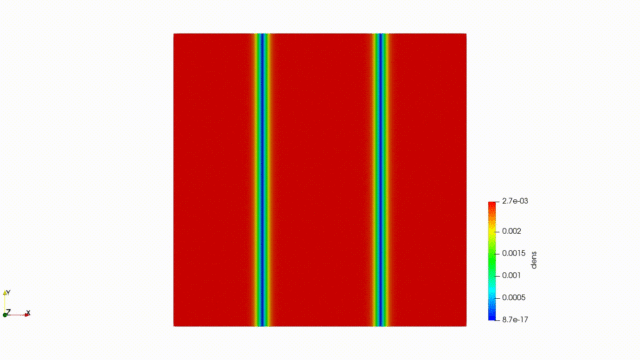
実際シミュレーションしてみるとこのような結果になります。
ぐっちゃぐちゃになってしまいました。
後退差分
つぎは後退差分でやってみましょう。

\begin{align*}\frac{T^{n+1}_{i}-T^{n}_{i}}{\Delta t}+u\frac{T^{n}_{i}-T^{n}_{i-1}}{\Delta x}=0\end{align*}
なので、\(\alpha=\frac{u\Delta t}{\Delta x}>0\)と置くと、
\begin{align*}T^{n+1}_{i}=T^{n}_{i}-\alpha\bigg(T^{n}_{i}-T^{n}_{i-1}\bigg)\tag{9}\end{align*}
となり、(9)式を数値計算で解くことになります。
これをもう少し式変形変形すると、
\begin{align*}T^{n+1}_{i}=(1-\alpha)T^{n}_{i}+\alpha T^{n}_{i}\tag{10}\end{align*}
となります。
これは、\(\alpha=\frac{u\Delta t}{\Delta x}<1\)としておけば、(10)式の右辺は必ず正の値を取っているので前進差分のような変な振動は起こらなさそうであることがわかります。
実際シミュレーションしてみるとこのような結果になります。
前進差分のような変な振動はなくなりましたが、形を変えずに速度\(u\)で移動するという数値計算結果にはなっていないようです。
これは、(11)式のように
\begin{align*}T^{n+1}_{i}=(1-\alpha)T^{n}_{i}+\alpha T^{n}_{i}\tag{11}\end{align*}
\((1-\alpha)T^{n}_{i}+\alpha T^{n}_{i}\)の部分が、\(i+1\)と\(i\)の割合で\(T^{n+1}_{i}\)を求めているため、角の部分がならされてしまうために起こっていると考えられます。
空間の離散化をもっと細かくすれば改善されるかもしれませんが、計算時間がかかることになりますし、空間の刻みを細かくしただけでは根本的な解決には至らないと思われるので別の数値解法が必要であるかもしれません。
中心差分
次は中心差分で解いてみましょう。
\begin{align*}\frac{T^{n+1}_{i}-T^{n}_{i}}{\Delta t}+u\frac{T^{n}_{i+1}-T^{n}_{i-1}}{2\Delta x}=0\end{align*}
なので、\(\alpha=\frac{u\Delta t}{\Delta x}>0\)と置くと、
\begin{align*}T^{n+1}_{i}=T^{n}_{i}-\frac{1}{2}\alpha\bigg(T^{n}_{i+1}-T^{n}_{i-1}\bigg)\tag{12}\end{align*}
となり、(12)式を数値計算で解くことになります。
これをもう少し式変形変形すると、
\begin{align*}T^{n+1}_{i}=-\frac{\alpha}{2}T^{n}_{i+1}+T^{n}_{i}+\frac{\alpha}{2}T^{n}_{i-1}\tag{13}\end{align*}
となります。
また右辺に負の項が存在することになります。
よって、数値解は振動するような振る舞いをすることが予想されます。
実際シミュレーションしてみるとこのような結果になります。

前進差分はぐっちゃぐちゃになりましたが、中心差分での結果は振動しながら右へ進んでいっているのがわかります。
まとめ
1次元の移流方程式を、
で解いてみました。
結果は以下のような感じです。
 後退差分での結果が一番良い結果ということになりました。
後退差分での結果が一番良い結果ということになりました。
これは速度の空間微分を流れの風上側を使って解くため、風上差分と呼ばれる差分法です。
速度\(u\)の値が正の値を取っていたので、「後退差分の結果がまとも」という結果になりましたが、
速度の値が負の値を取っている場合は「前進差分の結果がまとも」ということになります。
流れの向きを考えて差分法を考えないといけないという良い教訓になりました。
しかし、必ず流れが一方向だけという現象はめったにないので、どの方向から流れあったとしても安定的に解いてくれる数値解法を考える方が賢明かと思います。
空間の2次精度である中心差分よりも、1次精度の後退差分の方が比較的良い結果を得られているのは面白いです。
空間の2次精度とはテーラー展開の何次の項まで残すかに依るものですが、とにかく高次の項まで残せば良いというものではなく、解くべき方程式の特徴を掴んで数値計算することが大事であるということを教えてくれる結果となりました。
Fortranソースコードのzipファイルと実行の方法
本記事で紹介した計算結果は、下記よりzipファイルを入手して解凍することで再現できます。
そして、以下のようにコマンドを打てばFortranが実行され、gnuplotでのアニメーションを確認することができます。
|
|
gfortran 1D_iryu_1Eq.f90 ./a.out gfortran movie_script.f90 ./a.out >movie gnuplot movie |