こんにちは(@t_kun_kamakiri)
流体解析と聞くと、「数式が難しそう」「専門家しかできない」といった印象を持つ方も多いかもしれません。
この記事では、無料で使えるオープンソースツールである SALOME と OpenFOAM を使い、配管合流部の流れを実際に計算・可視化するまでの流れを、できるだけやさしく解説していきます。
- OpenFOAMを触ってみたいけれど、何から始めればいいのかわからない
- まずは一つ、最後まで計算を回してみたい
そんな方が、最初の一歩を踏み出すための記事になることを目指しています。
salome 9.15.0
OpenFOAM v2412
SALOMEのインストール
salomeのダウンロードはこちらから行います。
zipファイルでダウンロードして適当なフォルダで解凍すると使用することができます。
解凍が済んだらrun_salome.batをダブルクリックするとsalomeが起動します。

OpenFOAMのインストール
OpenFOAMの使用環境はWSL2(WindowsでのLinux環境)を想定しています。
SALOMEでメッシュ作成
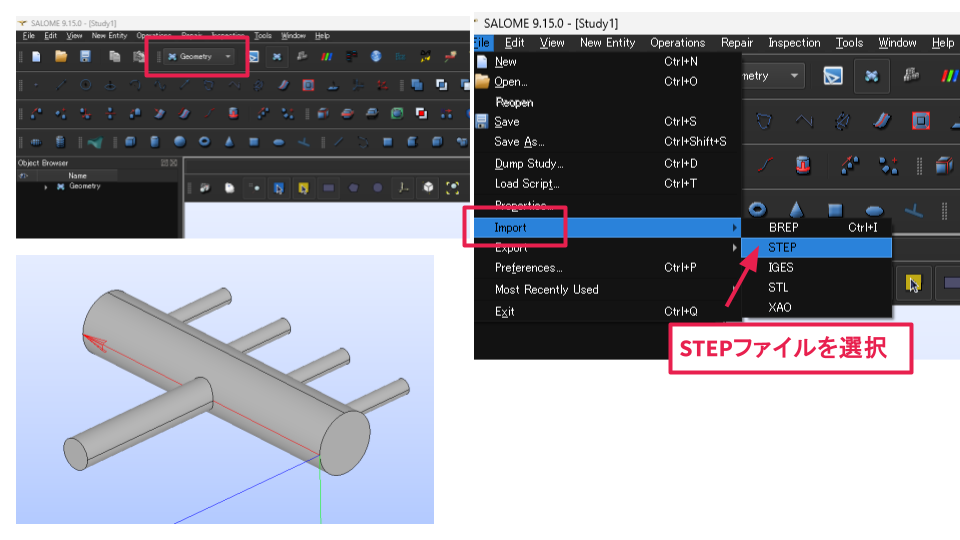
上部のモジュール選択で Geometry を選びます(画像の「Geometry」が赤枠のところ)。
- File → Import → STEP
- STEPファイルを選択して読み込み
読み込み後、Object Browser(左側)に Solid などの形状が表示されます。
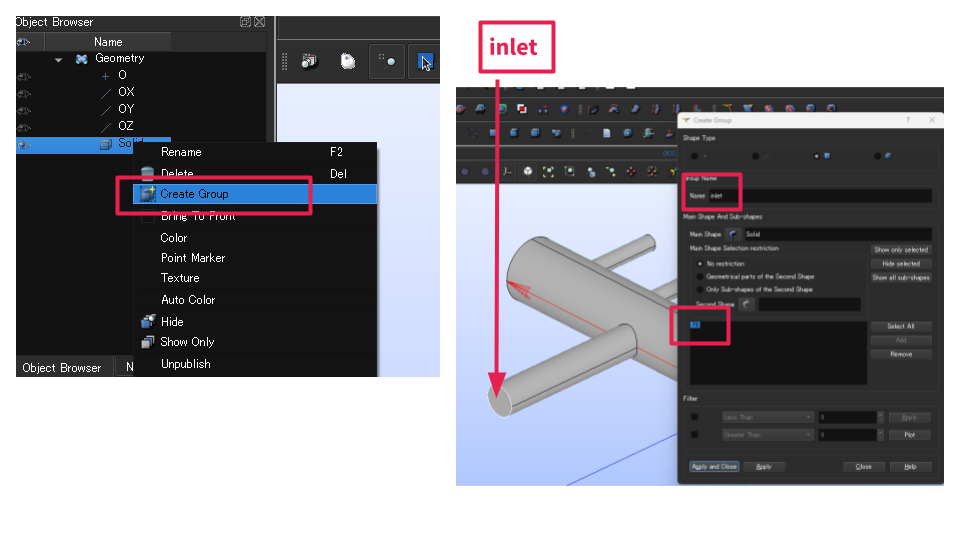
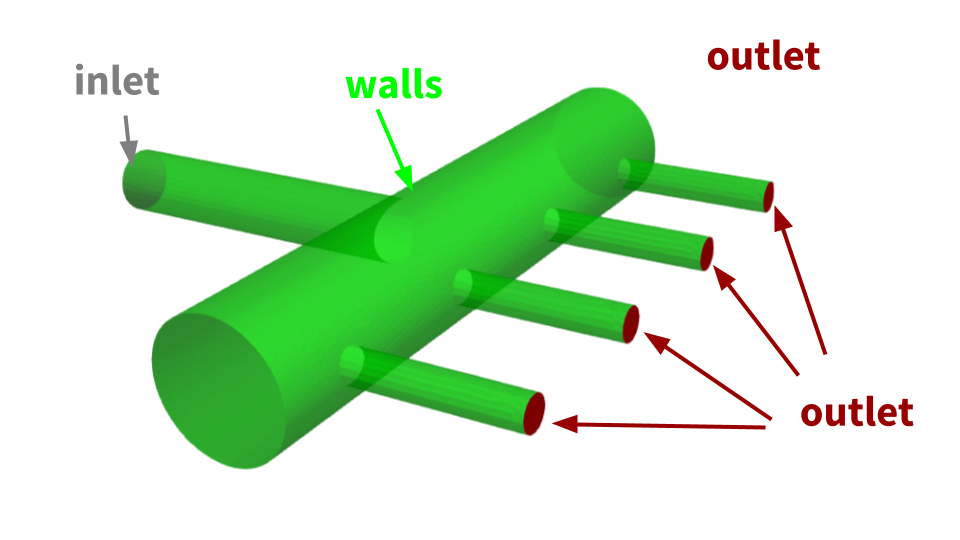
続いて、境界を「Group」として作ります(inlet / outlet / walls)
OpenFOAMなどに渡すときは、ここで作る Group名が境界名 になります。
(ここが一番大事)
inlet グループ作成
- Object Browserで Solid を右クリック
- Create Group を選択
- ダイアログで
- Name:
inlet - 選択対象(Face/Surface)を「面」にする(通常、作るのは面グループ)
- Name:
- 画面上で 入口面 をクリックして選択 → Add(もしくはApply)
→ inletグループ完成
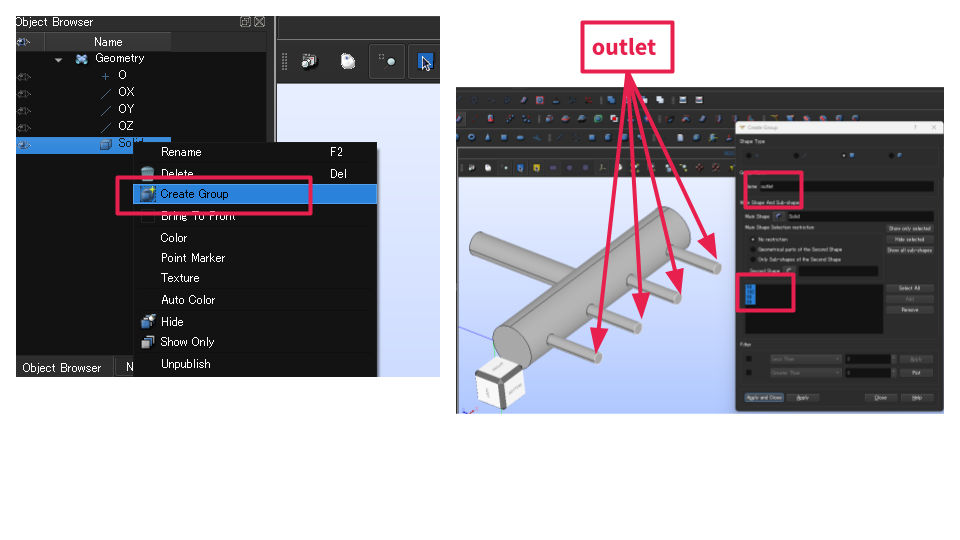
3-2) outlet グループ作成(複数面ある場合)
同様に:
- Solid右クリック → Create Group
- Name:
outlet - 出口の面を 必要な数だけ選んで Add
(画像では複数の枝管の出口面が全部outletになってます)
3-3) walls グループ作成(それ以外全部)
- Solid右クリック → Create Group
- Name:
walls - inlet/outlet以外の面をまとめて walls にする
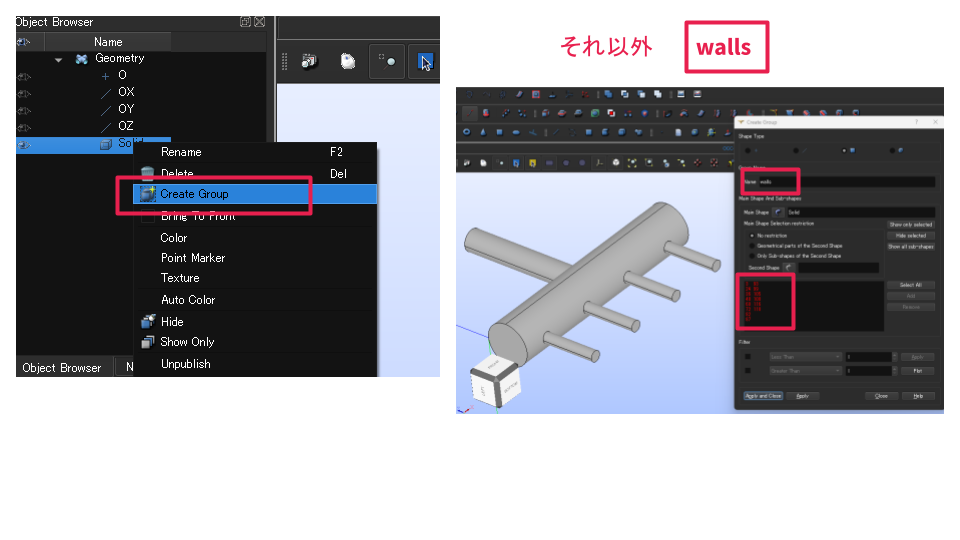
続いてメッシュ作成に移ります。
上部のモジュール選択で Mesh に変更します(画像のMesh赤枠)。
メニューから
- Mesh → Create Mesh
すると「Edit mesh」画面が出ます。
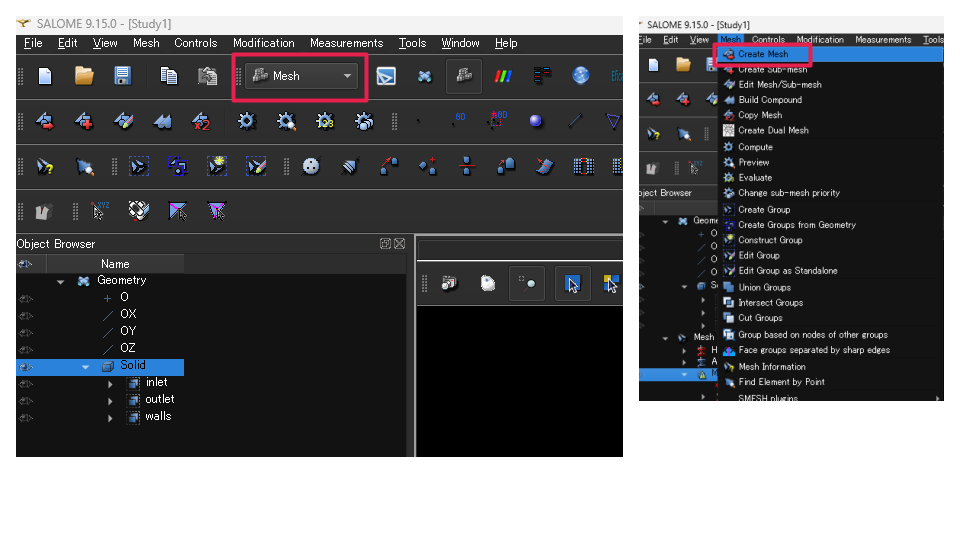
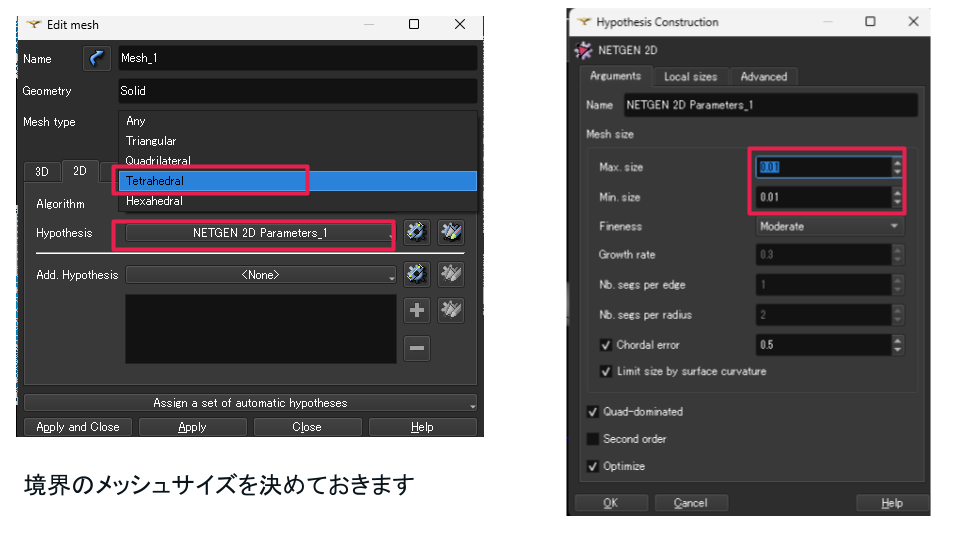
まずは表面メッシュサイズを作成します。
Mesh typeはAnyでも良いですが、変なメッシュができてしまいOpenFOAMでの変換が上手くいかなくなるので、Tetrahedralにしました。
メッシュサイズはMax 0.01、Min 0.01とします。
Object Browserで Mesh_1 を右クリックしてComputeします。
成功すると、メッシュが表示され、要素数などの結果ウィンドウが出ます(画像のメッシュ統計の画面)。
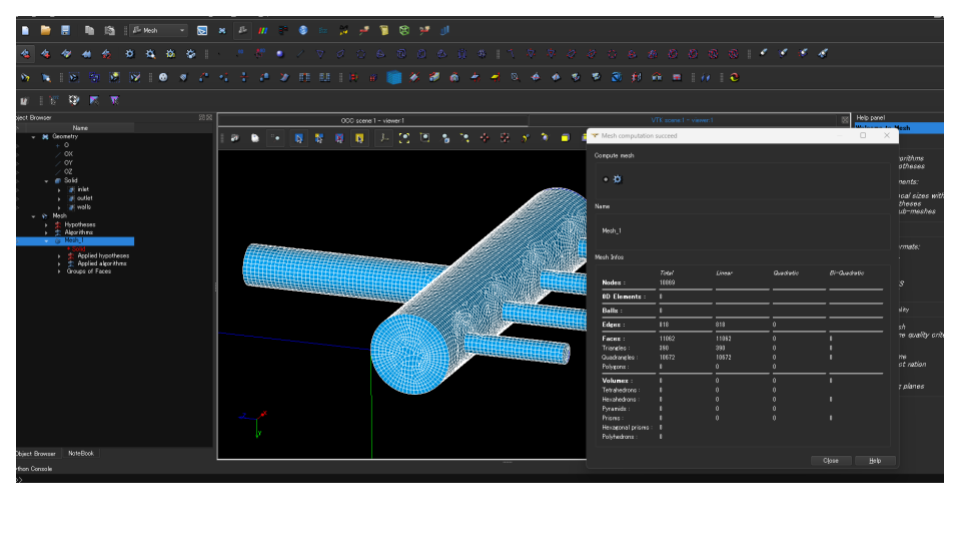
まだ表面のメッシュが作成されただけなので、3D体積メッシュ(Tetrahedral)+NETGENを選び内部領域のメッシュを作成します。
「Edit mesh」画面でだいたい以下の設定にします(画像の通り)
- Algorithm(3D):Tetrahedral(テトラ)
- Hypothesis:NETGEN 2D Parameters(境界サイズ用)や NETGEN 3D(体積用)が見えるはず
※SALOMEの構成によって表示順が少し違うことがありますが、基本は「NETGEN」でOKです。
境界層(Viscous Layers)を walls にだけ追加
ここが「境界層メッシュ」の設定です。
Edit mesh 画面で
- Add Hypothesis → Viscous Layers を追加
(または Hypothesis の横のアイコンから)
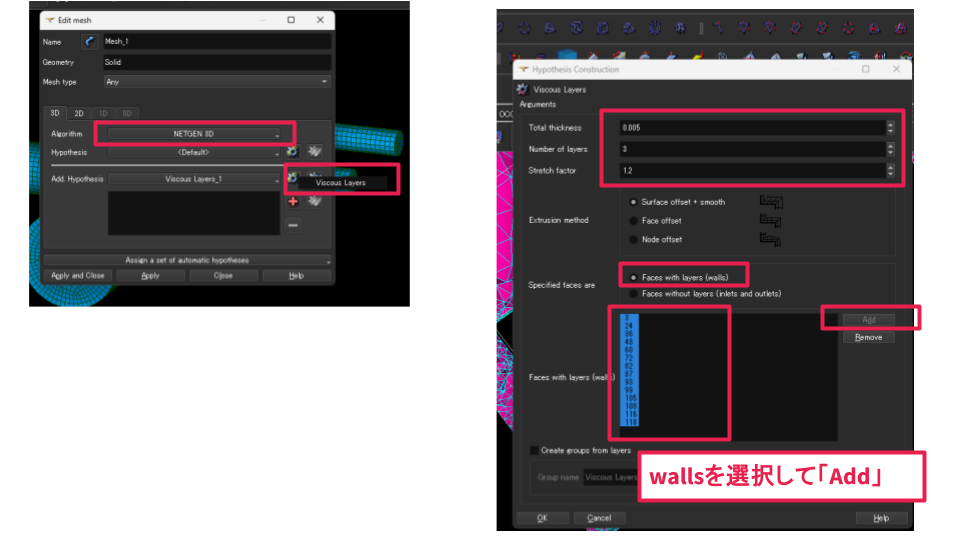
Viscous Layers の画面で主に触るのは:
- Total thickness:境界層の総厚み
- Number of layers:層数
- Stretch factor:層の成長率(外側に向かって厚くする倍率)
- walls を指定して Add
- Faces with layers (walls) を選ぶ
- リストから walls グループ を選んで Add
(画像の「wallsを選択して[Add]」のところ)
重要:inlet/outlet には境界層を付けないのが一般的です。
walls だけに付けるのが基本です。
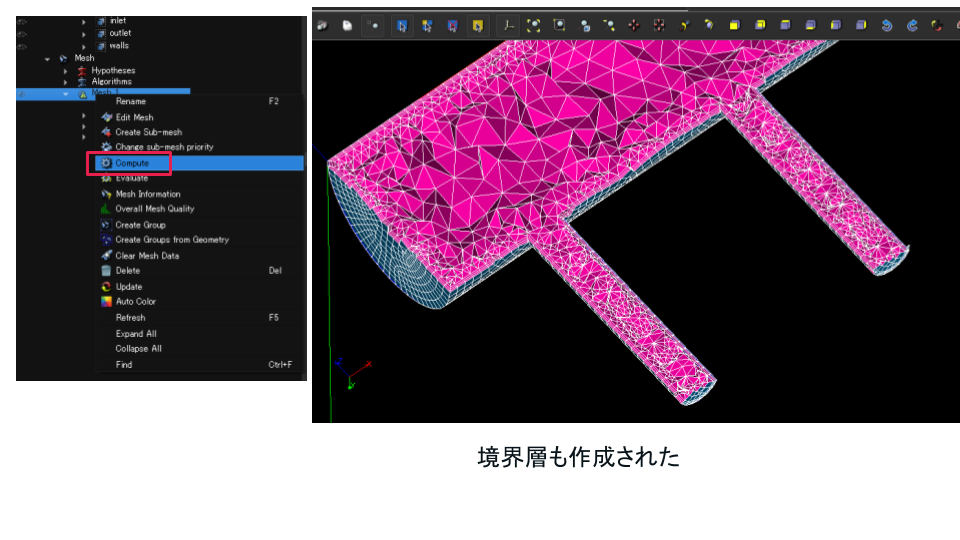
Viscous Layers 設定後に再度「Mesh_1 右クリック → Compute」します。
境界付近に層状の要素ができているのが確認できます(画像の「境界層も作成された」)。
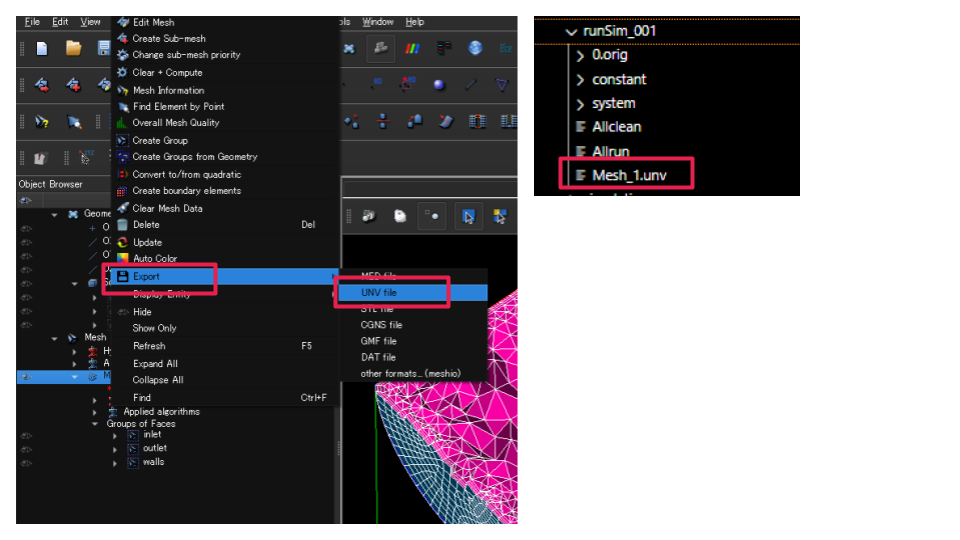
最後に書き出し。
- Mesh_1 を右クリック → Export → UNV file
- 例:
Mesh_1.unvとして保存
保存先フォルダに Mesh_1.unv が作成されます(画像右側のファイルツリー)。
OpenFOAMの計算設定
ここからはsalomeで作成したメッシュ情報からOpenFOAMの設定を行います。
まずはsalomeからOpenFOAMへのメッシュ変換にあたってダミーのOpenFOAMファイルケースが必要なので、チュートリアルから作業フォルダにコピーします。
|
1 |
cp -r $FOAM_TUTORIALS/incompressible/simpleFoam/pipeCyclic/* . |
$FOAM_TUTORIALS = /usr/lib/openfoam/openfoam2412/tutorials
コピーするチュートリアルは計算対象と近いモデルを持ってくる方があとあと設定などが類似しているので楽です。
以下のコマンドでsalomeで作成したメッシュをOpenFOAM形式へ変換します。
|
1 |
ideasUnvToFoam Mesh_1.unv |
以下のように既にsalomeで設定したパッチ名がOpenFOAMの境界面として割り当てられています。
|
1 2 3 4 5 6 7 8 9 10 11 |
Sorting boundary faces according to group (patch) 0: inlet is patch 1: outlet is patch 2: walls is patch Constructing mesh with non-default patches of size: inlet 284 outlet 344 walls 21624 End |
constant/polyMesh/bounaryを確認して、変更が必要な個所は変更を行います。
ここでは、境界名wallsは壁条件としたいので「type wall;」に変更します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
3 ( inlet { type patch; nFaces 284; startFace 306414; } outlet { type patch; nFaces 344; startFace 306698; } walls { type wall; nFaces 21624; startFace 307042; } ) |
ParaViewで確認しておきましょう。
ParaViewでの確認は以下のコマンドで空ファイルを作成し、それを読み込むことでモデルの表示がされます。
|
1 |
touch post.foam |
問題なさそうでしたらOpenFOAMの設定に進みます。
今回は変更した箇所だけを示します。
境界条件の設定(層流のみの場合)
0/U
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
dimensions [0 1 -1 0 0 0 0]; internalField uniform (0 0 -1); boundaryField { inlet { type fixedValue; value uniform (0 0 -1); } outlet { type zeroGradient; } walls { type noSlip; } } |
0/p
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { inlet { type zeroGradient; } outlet { type fixedValue; value uniform 0; } walls { type zeroGradient; } } |
層流条件で計算させる場合はここまでが必須になります。
乱流初期条件に用いる ($k$) と ($\epsilon$) の求め方
今回コピーしたチュートリアルは乱流モデルが使用されています。
constant/turbulenceProperties
|
1 2 3 4 5 6 7 8 9 10 |
simulationType RAS; RAS { RASModel realizableKE; turbulence on; printCoeffs on; } |
OpenFOAM で RANS 乱流モデル(例:($k$)-($\epsilon$) モデル)を用いる場合,
計算開始時に 乱流運動エネルギー ($k$) と 散逸率 ($\epsilon$) の初期値を与える必要があります。
ここでは、乱流強度と代表長さから求める一般的な方法を整理します。
乱流運動エネルギー (k)
乱流運動エネルギー (k) は,乱流強度 (I) と代表流速 (U) を用いて次式で定義されます。
今回用いた条件は以下の通りです。
これを代入すると,
となります。
散逸率 (\epsilon)
散逸率 ($\varepsilon$) は、乱流モデル定数 ($C_\mu$)、乱流運動エネルギー ($k$)、および代表長さ ($L$) を用いて次式で与えられます。
よって、
となります。
境界条件の設定(乱流モデルの場合)
0/k
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0.00375; boundaryField { #includeEtc "caseDicts/setConstraintTypes" inlet { type turbulentIntensityKineticEnergyInlet; intensity 0.05; // 5% turbulent intensity value $internalField; } outlet { type zeroGradient; } walls { type kqRWallFunction; value uniform 0; } } |
0/epsilon
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
dimensions [0 2 -3 0 0 0 0]; internalField uniform 0.125; boundaryField { #includeEtc "caseDicts/setConstraintTypes" inlet { type turbulentMixingLengthDissipationRateInlet; mixingLength 0.5; // 0.5m - half channel height value $internalField; } outlet { type zeroGradient; } walls { type epsilonWallFunction; value uniform 0; } } |
0/nut
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
dimensions [0 2 -1 0 0 0 0]; internalField uniform 1e-05; boundaryField { inlet { type calculated; value uniform 1e-05; } outlet { type calculated; value uniform 1e-05; } walls { type nutkWallFunction; value uniform 0; } } |
0/nuTilda
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
boundaryField { inlet { type fixedValue; value uniform 1e-05; } outlet { type zeroGradient; } walls { type fixedValue; value uniform 0; } } |
結果

まとめ
今回はsalomeからメッシュ作成を行い、OpenFOAMで流体解析を行うまでの流れを解説しました。
salomeを使ったメッシュ作成はこちらの記事もご参考ください。
バックステップ流れ解説記事(単相流)
- 【第1回バックステップ流れ】SalomeのShaperを使ってモデル作成をしてみた。
- 【第2回バックステップ流れ(動画あり)】Salomeでメッシュ作成してみた。2次元のバックステップ流れ。
- 【第3回バックステップ流れ】OpenFOAMで流体解析!層流モデルと乱流モデル(k-ωSST)で計算。