どうも(^^)/
最近は、ハミルトンの正準方程式を導出するのに色々なやり方を試しています。
ラグランジュ方程式を導出するのに色々なやり方があったように、それと等価なハミルトンの正準方程式も色々なやり方があると思うのですよね。
本記事の内容
最小作用の原理からハミルトンの正準方程式を導出する。
ハミルトンの正準方程式:
ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)に対して
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}
\cdot\cdot\cdot (1)\end{align*}
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}
\cdot\cdot\cdot (2)\end{align*}
それでは、まずは最小作用の原理の復習からやっていきましょう(^^)/
復習:最小作用の原理
簡単に「さらっ」っと復習します(^^)/
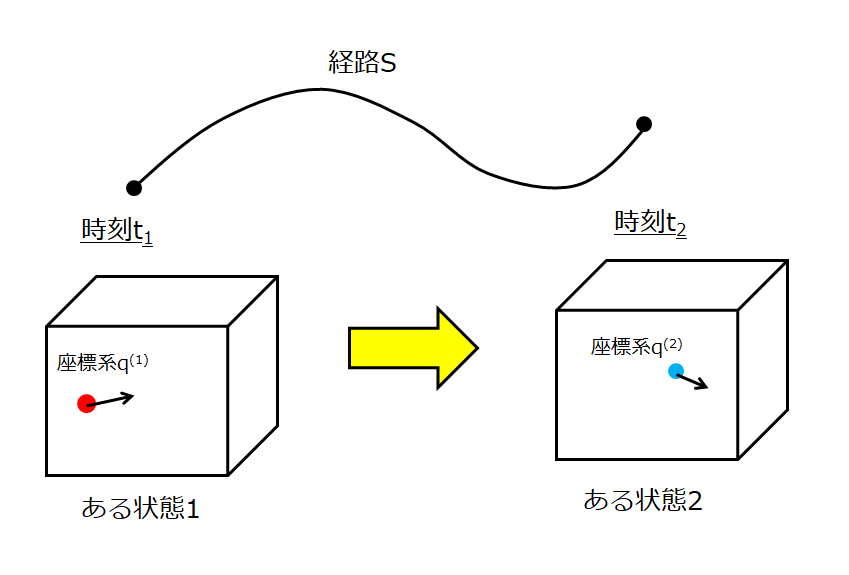
ある時刻における<<力学的状態>>は、一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)で決まります。
その状態を一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を変数として、ラグランジアン\(L\)として関数と置くのでした。
そして最小作用の原理を考えるにあたって、下記のようにある状態1からある状態2にいく経路というものをイメージします。

そうすると、”状態” 経路みたいなものは、
\begin{align*} S=\int_{t_{1}}^{t_{2}}L(\{q_{i}\},\{\dot{q}_{i}\},t)dt\end{align*}
となりますね。
これを作用といいます。
それで「一般座標\(q_{i}\)と一般速度\(\dot{q}_{i}\)を変数とするラグランジアン\(L\)によって色々変わるのですが、<<力学的な状態>>というのは作用Sが最小(停留点)を取っているときである」・・・・・このことを最小作用の原理と言います。
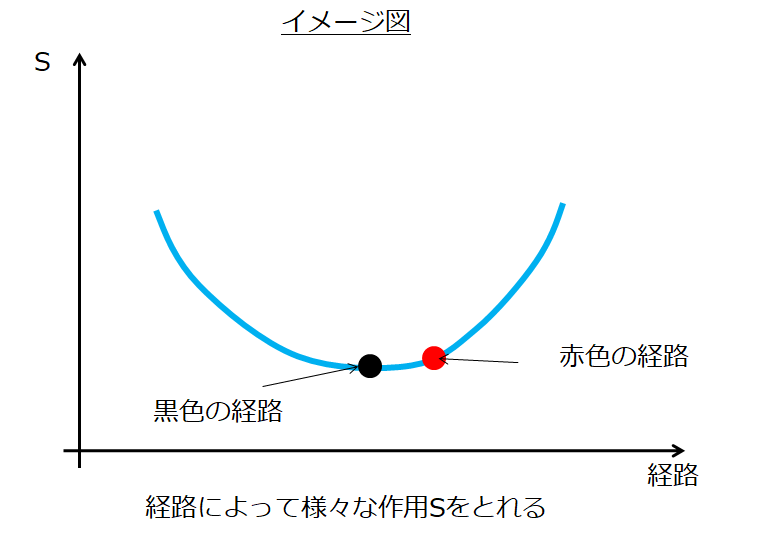
イメージは↓です。

すると、\(\delta q_{i}(t)\)のようなわずかなずれ(変分)を考えます。
ただ端は固定されているものとして、\(\delta q_{i}(t_{1})=\delta q_{i}(t_{2})=0\)です。
最小作用の原理は、
\begin{align*}\delta S=\int_{t_{1}}^{t_{2}}L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\},t)dt-\int_{t_{1}}^{t_{2}}L(\{q_{i}\},\{\dot{q}_{i}\},t)dt\end{align*}
とおくと、作用\(S\)は上の絵の●のところで停留点をとっているのですから、
\(\delta S=0\)ですよね。
すなわち
\begin{align*}\int_{t_{1}}^{t_{2}}\big(L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\},t)-L(\{q_{i}\},\{\dot{q}_{i}\},t)\big)dt=0\cdot\cdot\cdot (3)\end{align*}
と、このように書けます。
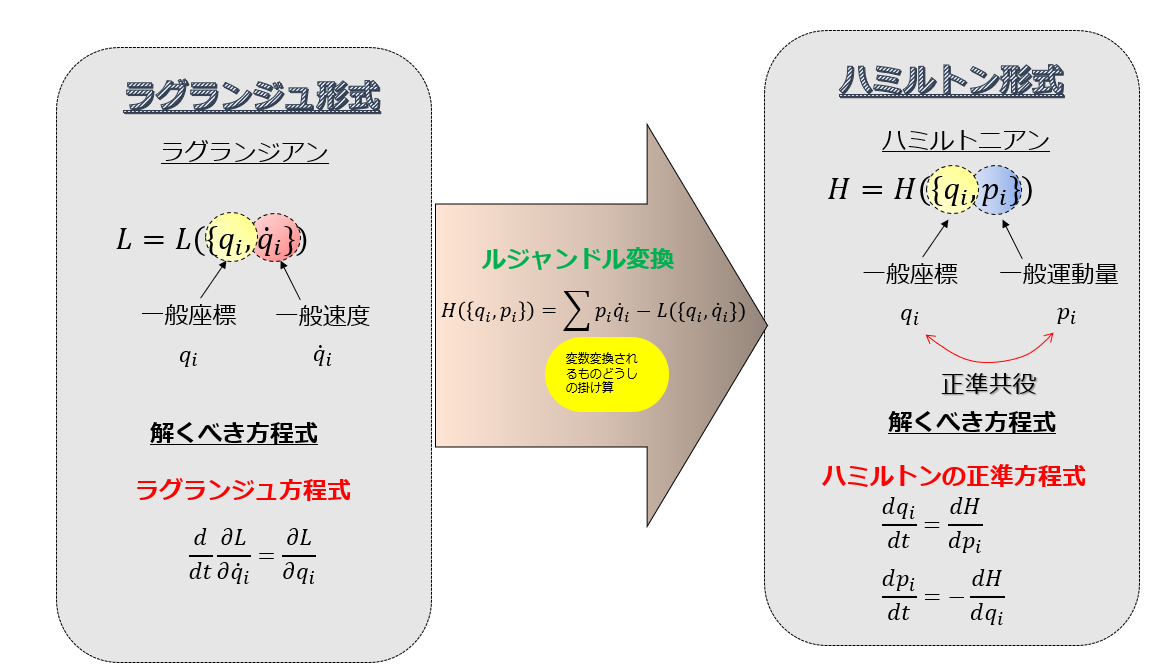
最小作用の原理の使ってハミルトンの正準方程式を導出する手続きは、(3)式を使って、
\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\end{align*}
により、ラグランジアン\(L\)からハミルトニアン\(H\)にすることに他なりません。
それでは地道に計算していくだけです(^^)/
(3)式を使って\(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\)により、ラグランジアン\(L\)からハミルトニアン\(H\)にする
さて、地道にゴリゴリ計算していきます。
\begin{align*}\int_{t_{1}}^{t_{2}}\big(L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\},t)-L(\{q_{i}\},\{\dot{q}_{i}\},t)\big)dt=0\cdot\cdot\cdot (3)\end{align*}
(3)式の積分される関数は、
\begin{align*}\delta L=L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\})-L(q_{i},\dot{q}_{i})\cdot\cdot\cdot (4)\end{align*}
と、書いておきます。
※\(t\)は邪魔なので省略しておきます。ある時刻における<<力学的な状態>>はどのような式に従うのかを見たいので、\(t\)に陽に依存しないとして計算します。
時刻によって運動方程式やら変わらないですよねって感じです(笑)
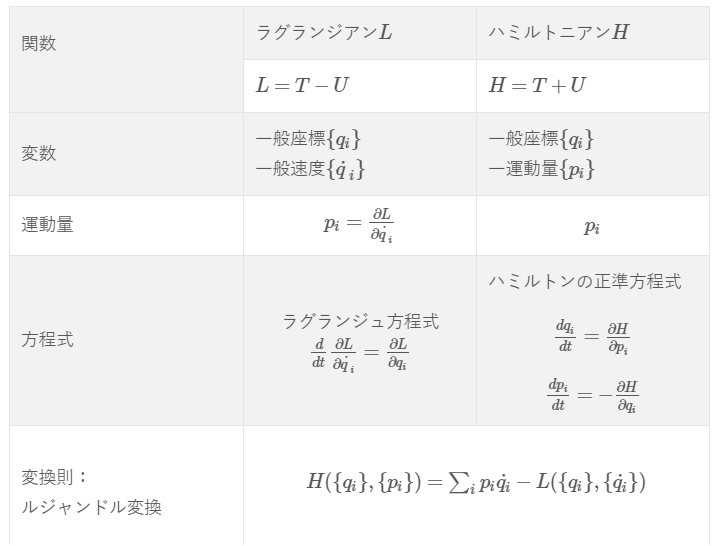
ルジャンドル変換の\(H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\)より、
\begin{align*}L(\{q_{i}\},\{\dot{q_{i}}\})=\sum_{i}p_{i}\dot{q_{i}}-H(\{q_{i}\},\{p_{i}\})\end{align*}
として(4)式に代入していきます。
※ルジャンドル変換は↓こちらを参照ください。
\begin{align*}\delta L=L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\})-L(q_{i},\dot{q}_{i})\end{align*}
\begin{align*}=\big(\sum_{i}(p_{i}+\delta p_{i})(\dot{q}_{i}+\delta \dot{q}_{i})-H(\{q_{i}+\delta{q_{i}}\},\{p_{i}+\delta p_{i}\})\big)\end{align*}
\begin{align*}-\big(\sum_{i}p_{i}\dot{q_{i}}-H(\{q_{i}\},\{p_{i}\})\big)\cdot\cdot\cdot (5)\end{align*}
ちょっと煩雑になってきたのでひとつひとつ計算しましょう。
(第一項)ー(第三項)
\begin{align*}=\sum_{i}(p_{i}\dot{q}_{i}+p_{i}\delta \dot{q}_{i}+\dot{q}\delta p_{i}+\delta p_{i}\delta \dot{q})-\sum_{i}p_{i}\dot{q}_{i}\end{align*}
\begin{align*}=\sum_{i}(p_{i}\delta \dot{q}_{i}+\dot{q}_{i}\delta p_{i})\end{align*}
※ここでは、\(\delta \dot{q}_{i},\delta p_{i}\)に対する2次以上は無視しました。
(第二項)ー(第四項)
\begin{align*}=-\sum_{i}\big(\frac{\partial H}{\partial q_{i}}\delta q_{i}+\frac{\partial H}{\partial p_{i}}\delta p_{i}\big)\end{align*}
計算が終わりましたので、上の結果より(5)式が、
\begin{align*}\delta L=\sum_{i}(p_{i}\delta \dot{q}_{i}+\dot{q}_{i}\delta p_{i})-\sum_{i}\big(\frac{\partial H}{\partial q_{i}}\delta q_{i}+\frac{\partial H}{\partial p_{i}}\delta p_{i}\big)\cdot\cdot\cdot (6)\end{align*}
となりました。
そしてこの(6)式を、(3)式に代入しましょう。
\begin{align*}\int_{t_{1}}^{t_{2}}\bigg(\sum_{i}(p_{i}\delta \dot{q}_{i}+\dot{q}_{i}\delta p_{i})-\sum_{i}\big(\frac{\partial H}{\partial q_{i}}\delta q_{i}+\frac{\partial H}{\partial p_{i}}\delta p_{i}\big)\bigg)dt=0\end{align*}
↓Σと∫を入れ替えます。
\begin{align*}\sum_{i}\int_{t_{1}}^{t_{2}}\bigg((p_{i}\delta \dot{q}_{i}+\dot{q}_{i}\delta p_{i})-\big(\frac{\partial H}{\partial q_{i}}\delta q_{i}+\frac{\partial H}{\partial p_{i}}\delta p_{i}\big)\bigg)dt=0\cdot\cdot\cdot (7)\end{align*}
いいところまで来ました♪
(7)式の第一項に対して部分積分してやります。
と、その前に・・・・・
\begin{align*}\delta \dot{q}_{i}=\delta \frac{dq_{i}}{dt}=\frac{d \delta q_{i}}{dt}\end{align*}
としておきます。
これを使うと、
\begin{align*}\int_{t_{1}}^{t_{2}}(p_{i}\delta \dot{q}_{i})dt=\int_{t_{1}}^{t_{2}}(p_{i}\frac{d}{dt}\delta q_{i})dt\end{align*}
\begin{align*}=\left [ p_{i}\delta q_{i} \right ]_{t_{1}}^{t_{2}}-\int_{t_{1}}^{t_{2}}(\dot{p}_{i}\delta q_{i})dt\end{align*}
\begin{align*}=-\int_{t_{1}}^{t_{2}}(\dot{p}_{i}\delta q_{i})dt\end{align*}
\begin{align*}\delta q_{i}(t_{1})=\delta q_{i}(t_{2})=0\end{align*}
なので最後の式で第一項が消えました。
これを使うと、(7)の第一項に使うと
\begin{align*}\sum_{i}\int_{t_{1}}^{t_{2}}\bigg((-\dot{p}_{i}\delta q_{i}+\dot{q}_{i}\delta p_{i})-\big(\frac{\partial H}{\partial q_{i}}\delta q_{i}+\frac{\partial H}{\partial p_{i}}\delta p_{i}\big)\bigg)dt=0\end{align*}
⇔
\begin{align*}\sum_{i}\int_{t_{1}}^{t_{2}}\bigg((-\dot{p}_{i}-\frac{\partial H}{\partial q_{i}})\delta q_{i}+(\dot{q}_{i}-\frac{\partial H}{\partial p_{i}})\delta p_{i})\bigg)dt=0\cdot\cdot\cdot (8)\end{align*}
この(8)式が、任意の\(\delta q_{i}\)と\(\delta p_{i}\)に対して成立するためには、
\begin{align*}-\dot{p}_{i}-\frac{\partial H}{\partial q_{i}}=0\end{align*}
\begin{align*}\dot{q}_{i}-\frac{\partial H}{\partial p_{i}}=0\end{align*}
ということですね。
すなわち、
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (9)\end{align*}
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (9)\end{align*}
とこうなります。
お!!
思っていた通りハミルトンの正準方程式が出てきましたね!(^^)!
まとめ
最小作用の原理からハミルトンの正準方程式を導出しました。
やったことは、
\begin{align*}\int_{t_{1}}^{t_{2}}\big(L(\{q_{i}+\delta{q_{i}}\},\{\dot{q}_{i}+\delta{\dot{q}_{i}}\},t)-L(\{q_{i}\},\{\dot{q}_{i}\},t)\big)dt=0\cdot\cdot\cdot (3)\end{align*}
に対して、
ラグランジュ\(L\)からハミルトニアン\(H\)への変換
\begin{align*}H(\{q_{i}\},\{p_{i}\})=\sum_{i}p_{i}\dot{q_{i}}-L(\{q_{i}\},\{\dot{q_{i}}\})\end{align*}
を(3)式に代入して、ゴリゴリ式変形をしてハミルトンの正準方程式を導出しました!(^^)!
ハミルトンの正準方程式
ハミルトニアン\(H(\{q_{i}\},\{p_{i}\})\)に対して
\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (10)\end{align*}
\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (9)\end{align*}
※(9)式は、符号を忘れないように気を付けましょう。