リウヴィリ（Liouville）の定理｜宇宙に入ったカマキリ

ようやくリウヴィリの定理を説明するところまで来ました。

ところでリウヴィリの定理は解析力学でも出てくる内容ですし、統計力学でも出てくるでしょう。

場合によっては、量子力学でも出てきますし、類似性を考えると非圧縮性の流体と物理的な意味は全く同じであります。

どうして解析力学や統計力学や量子力学でリウヴィリの定理が出てくるのかと言いますと、位相空間（座標と運動量）で力学的な状態を考えるからです。

いきなりリウヴィリの定理のお話を始めてしまいましたが、リウヴィリの定理の内容を下記に記載しておきましょう。

リウヴィリの定理
位相空間内の微小領域内の代表点がハミルトンの正準方程式に従うとき、その領域内の体積は変化しない。

始めて聞く人にはピンとこない内容でしょう(笑)

具体例は後にしましょう(笑)

具体例を考えた方がイメージが付きやすい場合が多いですが、具体例を考えるのは記事を書くこちらの労力も使ってしまいます(‘_’)

むしろ数学的な手続きを先にやって、「ほら、なるでしょう！！」ってやってしまってから、じっくり具体例とリウヴィリの定理の意味を考えていきたいと考えています。

リウヴィリの定理の概要
1. 代表点が時間発展しても位相空間内での面積（体積）は変わらない。
2. 代表点を正準変換したと解釈することもできる
\(det(J)=1\)の証明
まとめ
参考図書

リウヴィリの定理の概要

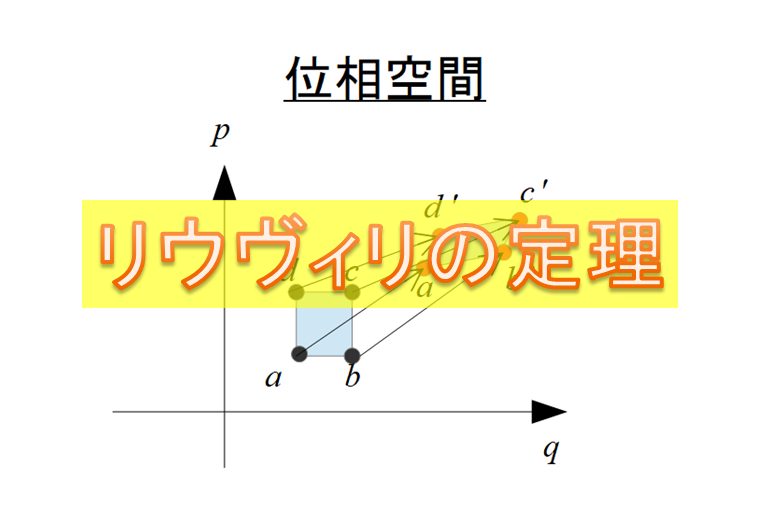
リウヴィリの定理は絵で書くと下記のようになります。

ここでは簡単に考えるために、運動の方向は\(q\)のみ（一次元）として考えます。

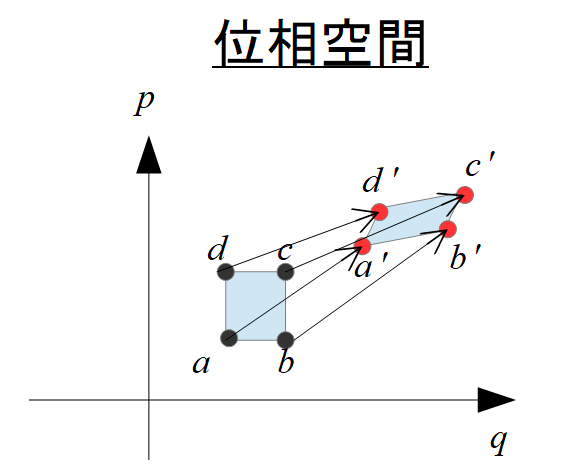
位相空間内に\(a,b,c,d\)の状態点が時刻\(t\)の時に与えられています。

この時の面積は、

面積：\(S\)

とします。

さらに、時刻\(t+\delta t\)で状態点が位相空間内を\({a}’,{b}’,{c}’,{d}’,\)と移動したとします。

その時の面積を、

面積：\({S}’\)

とします。

リウヴィリの定理に従うならば、\(S={S}’\)であると言っているのです。

ここで2通りの解釈ができるでしょう。

代表点が時間発展しても位相空間内での面積（体積）は変わらない。

まずひとつ目がこれです。

初期状態として、代表点\(a,b,c,d\)があったとします。

それを時間とともにずっと追跡するのです。

これを、流体の分野では物質粒子と言います。

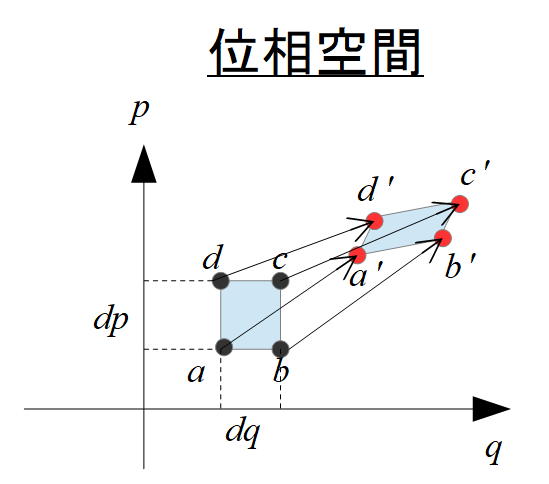
各代表点の座標は、

\begin{align*}a(q,p)\end{align*}

\begin{align*}b(q+\delta q,p)\end{align*}

\begin{align*}c(q+\delta q,p+\delta p)\end{align*}

\begin{align*}d(q,p+\delta p)\end{align*}

となります。

それが、時刻\(t+\delta t\)の時には、

\begin{align*}{a}'(Q(q,p),P(q,p))\end{align*}

\begin{align*}{b}'(Q(q+\delta q,p),P(q+\delta q,p))\end{align*}

\begin{align*}{c}'(Q(q+\delta q,p+\delta p),P(q+\delta q,p+\delta p))\end{align*}

\begin{align*}{d}'(Q(q,p+\delta p),P(q,p+\delta p))\end{align*}

となります。

これはどう考えているのかと言いますと、例えば\(a\)から\({a}’\)へ代表点が位相空間内で移動したときに、元々の代表点\((q,p)\)から移動して新しい代表点\((Q,P)\)に移動したと解釈します。

さらに代表点\((Q,P)\)はもともとの代表点\((q,p)\)に依存しているので、それが変数となっています。

ですので、時刻\(\delta t\)の間に

代表点\(a(q,p)\)

から

代表点\({a}'(Q(q,p),P(q,p))\)

に変化したとして、上記のように書きます。

時間とともに位相空間内を流れる代表点で作る面積（体積）が変わらないというリウヴィリの定理を\(S={S}’\)（数密度）と、これは非圧縮性の流体と全く同じになります。

上記の説明のように代表点を流体の物質粒子ととらえて時間について考えても良いのですが、時刻\(t\)を同じにしたまま各代表点を正準変換したと解釈することもできるでしょう。

それが以下の説明です。

代表点を正準変換したと解釈することもできる

時刻\(t\)を同じにしたまま各代表点を正準変換したと解釈します。

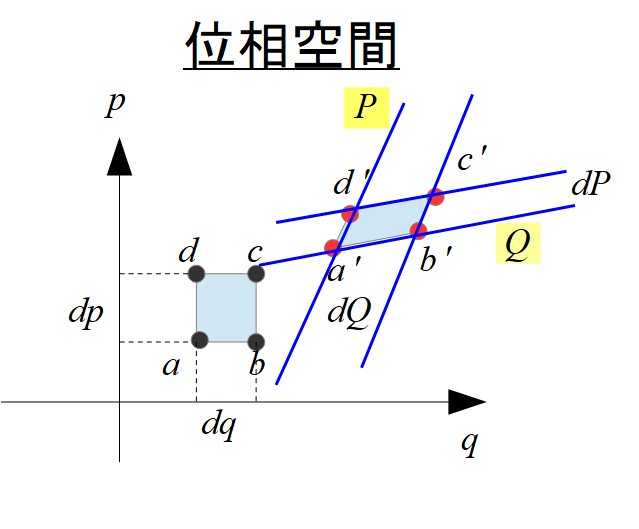
なので位相空間内で座標軸を書いてみると、↑こんな感じです。

新たに\(Q\)と\(P\)という変数に対する座標軸を作ってみました。

ここからようやくリウヴィリの定理の証明が始まります(笑)

たいした証明ではありません。

代表点\(Q,P\)は、元の変数\(q,p\)に依存しているので、

\begin{align*}Q=Q(q,p)\cdot\cdot\cdot (1)\end{align*}

\begin{align*}P=P(q,p)\cdot\cdot\cdot (2)\end{align*}

\({S}’\)は微小領域の\(dQ,dP\)で足し合わせると考えると、

\begin{align*}{S}’=\int dQdP\cdot\cdot\cdot (3)\end{align*}

となります。

そこで、\(dQ,dP\)の全微分、

\begin{align*}dQ=\frac{\partial Q}{\partial q}dq+\frac{\partial Q}{\partial p}dp\cdot\cdot\cdot (4)\end{align*}

\begin{align*}dP=\frac{\partial P}{\partial q}dq+\frac{\partial P}{\partial p}dp\cdot\cdot\cdot (5)\end{align*}

なので、これを行列式の形で書きます。

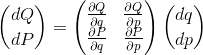
ここで\(dQdP\)は、

\begin{align*}dQdP=det|J|dqdp\cdot\cdot\cdot (6)\end{align*}

となります。

ここで、\(J\)はヤコビアン行列と言います。

それで、⑥を求めるのにこの\(J\)の行列式を計算すれば良いということになりますね。

2行2列の行列式はとても簡単で、対角線上にある式の掛け算の差を求めればよいのです。

\begin{align*}det(J)=|\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p}-\frac{\partial Q}{\partial p}\frac{\partial P}{\partial q}|\end{align*}

↑これを計算します。

その前に目標を確認しておきましょう。

リウヴィリの定理に依ると、位相空間内で、四角形\(a,b,c,d\)が作る面積\(S\)

\begin{align*}S=\int dqdp\cdot\cdot\cdot (7)\end{align*}

と、\({S}’\)が作る面積が変わらない・・・

すなわち、

\begin{align*}\int dqdp=\int dQdP\cdot\cdot\cdot (8)\end{align*}

を証明したいのです。

⑥式を見ると、

\(det(J)=1\)であることを証明すれば良いのです。

↑これが目標です。

\(det(J)=1\)の証明

\begin{align*}det(J)=|\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p}-\frac{\partial Q}{\partial p}\frac{\partial P}{\partial q}|\cdot\cdot\cdot (9)\end{align*}

ただ普通に計算して、これが１になってくれそうにありません。

もう一度リウヴィリの定理を思い出しましょう。

リウヴィリの定理
位相空間内の微小領域内の代表点がハミルトンの正準方程式に従うとき、その領域内の体積は変化しない。

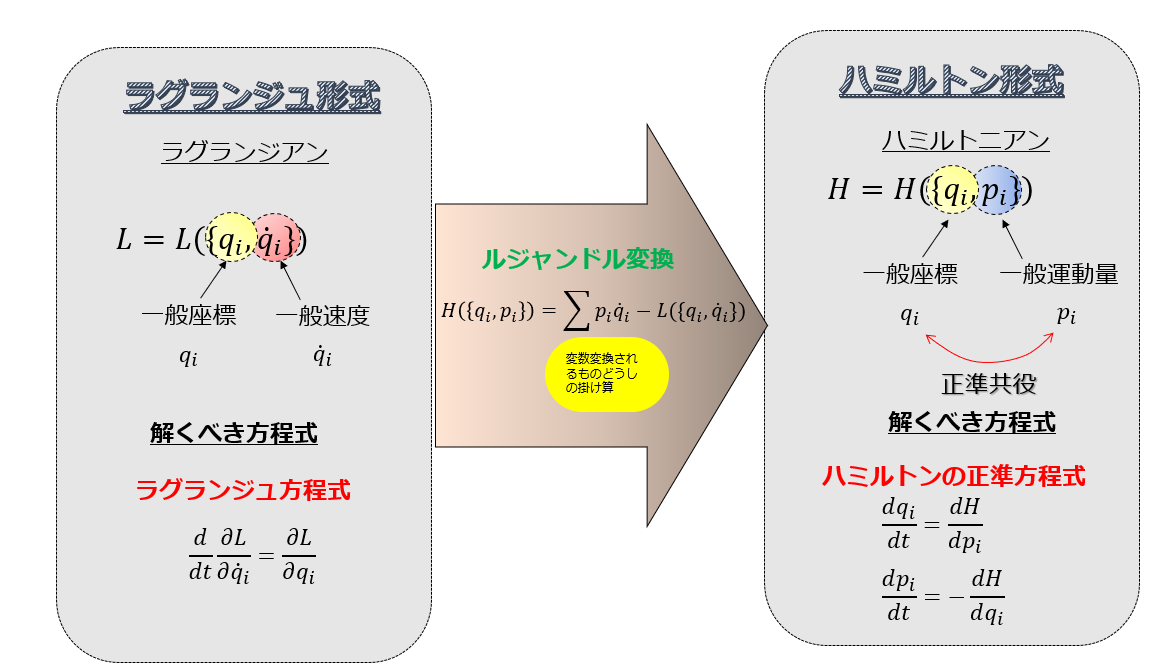
どうやらハミルトンの正準方程式を使えば良さそうです。

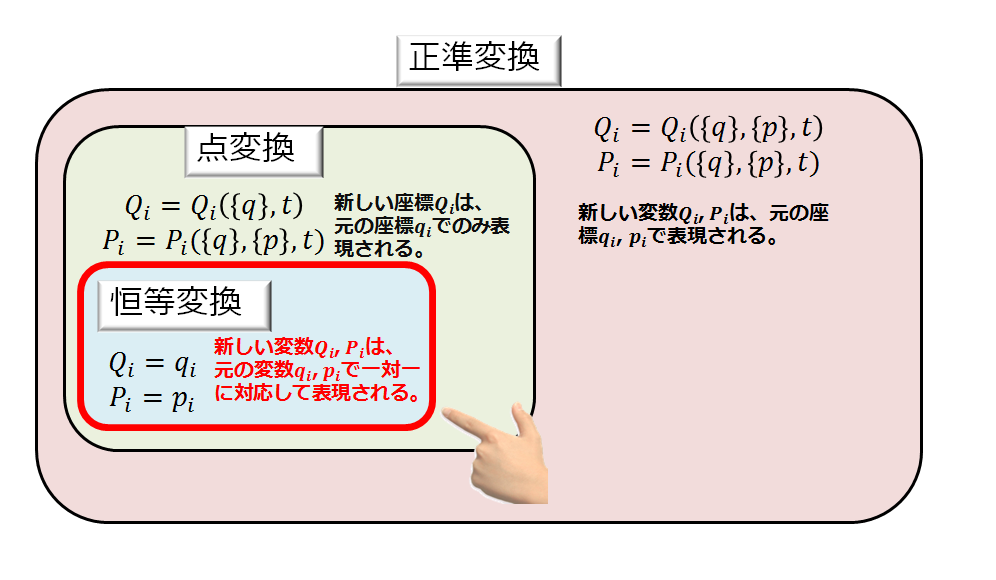
そういえば、⑨式の正準変換による変数\((q,p)\)と\((Q,P)\)の関係はちょうど前回の記事で書いていたのです!(^^)!

そのために↑この記事を書いたのです(笑)

この記事の内容に従うと、

\begin{align*}\big(\frac{\partial p_{i}}{\partial Q_{i}}\big)_{q_{i}}=-\big(\frac{\partial P_{i}}{\partial q_{i}}\big)_{Q_{i}}\cdot\cdot\cdot (10)\end{align*}

\begin{align*}\big(\frac{\partial p_{i}}{\partial P_{i}}\big)_{q_{i}}=\big(\frac{\partial Q_{i}}{\partial q_{i}}\big)_{P_{i}}\cdot\cdot\cdot (11)\end{align*}

\begin{align*}\big(\frac{\partial q_{i}}{\partial P_{i}}\big)_{p_{i}}=-\big(\frac{\partial Q_{i}}{\partial p_{i}}\big)_{P_{i}}\cdot\cdot\cdot (12)\end{align*}

\begin{align*}\big(\frac{\partial q_{i}}{\partial Q_{i}}\big)_{p_{i}}=\big(\frac{\partial P_{i}}{\partial p_{i}}\big)_{Q_{i}}\cdot\cdot\cdot (13)\end{align*}

が成り立ちます。

もちろん、これを導出する際にハミルトンの正準方程式が従うように\((q,p)\)から\((Q,P)\)へ変数変換したのですから、上記の関係式を使うことはハミルトンの正準方程式用いていることと等価であると言えましょう。

なので、上式を使ってしまいましょう(^^)/

※自由度は１なので、添え字の\(i\)はここでは特に関係はありません。

\begin{align*}det(J)=|\frac{\partial Q}{\partial q}\frac{\partial P}{\partial p}-\frac{\partial Q}{\partial p}\frac{\partial P}{\partial q}|\cdot\cdot\cdot (9)\end{align*}

について、

第一項は(13)式を、第二項は(10)を使うと、

\begin{align*}det(J)=|\frac{\partial Q}{\partial q}\frac{\partial q}{\partial Q}+\frac{\partial Q}{\partial p}\frac{\partial p}{\partial Q}|\cdot\cdot\cdot (14)\end{align*}

すると、右辺は、

\(q,p\)を変数とする関数\(Q\)に対する\(Q\)の微分であるので、

\begin{align*}|\frac{\partial Q}{\partial q}\frac{\partial q}{\partial Q}+\frac{\partial Q}{\partial p}\frac{\partial p}{\partial Q}|=|\frac{\partial Q(q,p)}{\partial Q}|=1\end{align*}

と、このように1になります。

つまり！！

\(det(J)=1\)であることを証明できました(^^)

ということになります。

これにて、リウヴィリの定理が証明できたのです。