本記事の目標
- 理想気体の状態方程式の式と条件
- 混合状態の理想気体の状態方程式
- ファンデルワールスの状態方程式(おまけ)
状態方程式ってどのように書くかご存知でしょうか?
1種類の気体だったらご存知ですよね(^^)
理想気体の状態方程式ですね。
僕はあえていつも理想気体と”理想”を付け加えています。
本記事は、混合ガスや理想気体の状態方程式が成り立たない場合の方程式もまとめようと思います!(^^)!
理想気体の状態方程式の式と条件
理想気体の状態方程式はよくご存じでしょうかね。
理想気体の状態方程式
\begin{align*}PV=nRT\end{align*}気体定数:\(R[J/K mol]\)
温度:\(T[K]\)
圧力:\(P[Pa]\)
モル数:\(n[mol]\)
容量:\(V[m^3]\)
条件
- 分子間力を無視できるほど希薄or分子間力を感じないほど高温(常温でも十分気体にとっては高温です)
- 分子の大きさを無視できるほど希薄(つまり気体)
なので液体などに理想気体の状態方程式は使えないですね。
これは1種類の気体に対しての状態方程式です。
複数の気体が混合している場合はどうなのでしょうか?
混合状態の理想気体の状態方程式
あまり混合状態での理想気体の状態方程式を見かけないので、まとめておきます。
混合状態とは、気体の種類が複数ある場合です。
例えば、「水素」「酸素」「二酸化炭素」・・・・など。
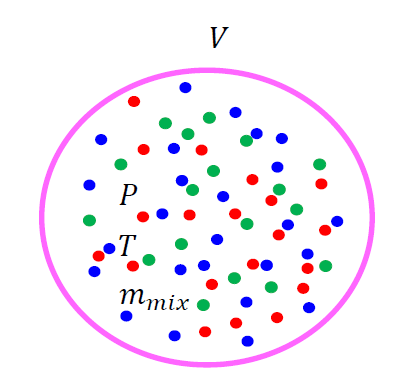
それぞれについて気体の状態方程式を立てます。
●気体:\(P_{1}V=\frac{m_{1}}{M_{1}}RT\)・・・(1)
●気体:\(P_{2}V=\frac{m_{2}}{M_{2}}RT\)・・・(2)
・
・
・
●気体:\(P_{n}V=\frac{m_{n}}{M_{n}}RT\)・・・(n)
気体定数:\(R[J/K mol]\)
温度:\(T[K]\)
圧力:\(P[Pa]\)
分子量:\(M[kg/mol]\)
容量:\(V[m^3]\)
単位に注意ですよ。特に気体定数。
(1)+(2)+・・・・+(n)をします。
ドルトンの分圧の法則(全圧力はそれぞれの気体分子が与える圧力の合計)より、
圧力については、\(P=P_{1}+P_{2}+・・・+P_{n}\)となりますので、
⇔
気体定数については、\(\tilde{R}_{i}=\frac{R}{M_{i}}\)とおいた。
※各気体の気体定数:\(\tilde{R}_{i}[J/K kg]\) 単位に注意
ここで、混合気体の気体定数を導入します。
これは各気体定数\(\tilde{R}_{i}\)に質量分率\(\chi_{i}\)をかけて足し合わせたものになっています。
(4)式を用いると(3)式より、混合状態の理想気体の状態方程式が求まります。
混合状態の理想気体の状態方程式
\begin{align*}PV=m_{mix}\tilde{R}_{mix}T\cdot\cdot\cdot (5)\end{align*}もしくは、
\begin{align*}P=\rho_{mix}\tilde{R}_{mix}T\cdot\cdot\cdot (5)\end{align*}※\(\rho_{mix}=\frac{m_{mix}}{V}\)
※各気体の気体定数:\(\tilde{R}_{i}[J/K kg]\) 単位に注意
\begin{align*}\tilde{R}_{mix}=\sum_{i}\frac{m_{i}}{m_{mix}}\tilde{R}_{i}(=\sum_{i}\chi_{i}\tilde{R}_{i})\cdot\cdot\cdot (4)\end{align*}\begin{align*}m_{mix}=\sum_{i}m_{i}\end{align*}
ファンデルワールスの状態方程式
理想気体の状態方程式で課している条件が成り立たないような状況下では、理想気体の状態方程式を補正する必要があります。
補正するのは以下の2つです。
- 分子の大きさを考慮
- 分子間力を考慮
分子の大きさを考慮
理想気体の状態方程式
これは分子を大きさのない質点だと考えていたので、実際は分子の容量は\(b\)あるのだよってことを加えればよいので、
分子間力を考慮
分子間力が働く場合は、どうなるのでしょうか?
理想気体の場合は、壁に与える力が圧力\(P\)として書かれていたのですが、分子間力で分子同士が引き合っていると、実際の圧力\({P}’\)は理想気体の圧力\(P\)より減りそうですよね。
どれくらい減るのか?
分子の単位体積当たりの数\(\frac{n}{V}\)の分だけ比例して減りそうですね。
数と言っても、本当の数は「\(n\)×アボガドロ数」ですがアボガドロ数は定数として考えているので無視しますね。
さらに、分子間力は相手があっての分子間力なので、\(\frac{n}{V}\)に比例するのではなくて、\(\frac{n}{V}\times \frac{n}{V}=\big(\frac{n}{V}\big)^2\)という形で比例することになります。
比例定数を\(a\)とおくと、実際の圧力は、
{P}’=P-a \big(\frac{n}{V}\big)^2\end{align*}
と、こうなります。
よって、ファンデルワールスの状態方程式は、理想気体の状態方程式から補正されて、
ファンデルワールスの状態方程式
\begin{align*}\big({P}’+\frac{a n^2}{V^2}\big)\big(V-nb \big)=RT\end{align*}⇔
\begin{align*}{P}’=\frac{RT}{V-nb}-\frac{a n^2}{V^2}\cdot\cdot\cdot (7)\end{align*}
まとめ
理想気体の状態方程式
\begin{align*}PV=nRT\end{align*}気体定数:\(R[J/K mol]\)
温度:\(T[K]\)
圧力:\(P[Pa]\)
モル数:\(n[mol]\)
容量:\(V[m^3]\)条件
- 分子間力を無視できるほど希薄or分子間力を感じないほど高温(常温でも十分気体にとっては高温です)
- 分子の大きさを無視できるほど希薄(つまり気体)
混合状態の理想気体の状態方程式
\begin{align*}PV=m_{mix}\tilde{R}_{mix}T\cdot\cdot\cdot (5)\end{align*}もしくは、
\begin{align*}P=\rho_{mix}\tilde{R}_{mix}T\cdot\cdot\cdot (5)\end{align*}※\(\rho_{mix}=\frac{m_{mix}}{V}\)
※各気体の気体定数:\(\tilde{R}_{i}[J/K kg]\) 単位に注意
\begin{align*}\tilde{R}_{mix}=\sum_{i}\frac{m_{i}}{m_{mix}}\tilde{R}_{i}(=\sum_{i}\chi_{i}\tilde{R}_{i})\cdot\cdot\cdot (4)\end{align*}\begin{align*}m_{mix}=\sum_{i}m_{i}\end{align*}
ファンデルワールスの状態方程式
\begin{align*}\big({P}’+\frac{a n^2}{V^2}\big)\big(V-nb \big)=RT\end{align*}⇔
\begin{align*}{P}’=\frac{RT}{V-nb}-\frac{a n^2}{V^2}\cdot\cdot\cdot (7)\end{align*}