こんにちは(@t_kun_kamakiri)
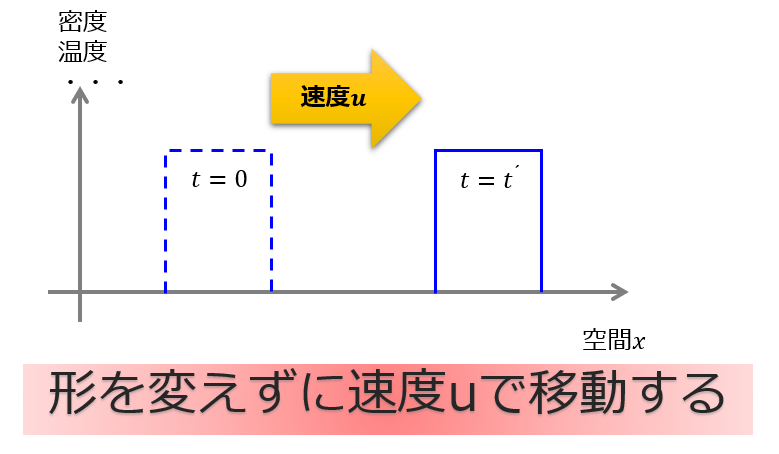
今回はOpenFOAMを使って移流方程式を解きたいと思います。その際に離散化スキームをどのように選択すると解の振る舞いが変わってくるのかを見ていきます。
前回の記事では移流方程式をの移流項を中心差分と風上差分で計算した結果を見ました。
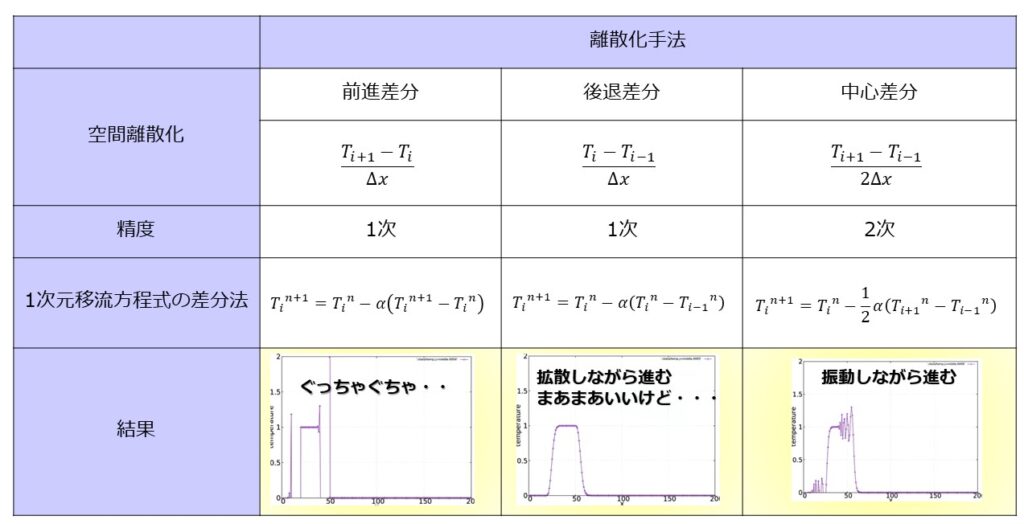
中心差分は解が振動してぐちゃぐちゃになり、風上差分は解が拡散しながら右に進行する解の振る舞いをしました。
風上差分で拡散するやつ#移流方程式 pic.twitter.com/xFUtG5nKWR
— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) February 1, 2023
色々なスキームを試しますが理論的な解説はここではしません。「スキームを変えると解の振る舞いがどう変わるのか」を知ってもらえればと思います。
勉強会でも「スキームがわからない」という質問もたまに聞くため、ナビエストークス方程式のような難しい方程式からせず、まずは今回のような簡単な移流方程式から体験すれば良いのではないかと思います。
スキームを手で変えていくのは面倒なのでPythonを使って自動実行しますので、その辺も参考になればと思います。
- OpenFOAMの移流方程式を使って色々なスキームでの解の振る舞いを見る。
- 計算の実行はPythonで自動化する
以前にも移流方程式を差分法を使ってFortranで解いたことがありますが、移流方程式は式が簡単で解析解があるにも関わらず数値的に解こうとすると、不安定だったり拡散してしまったり難しい問題があります。
このように、流体の第二項の対流項$u\frac{\partial T}{\partial x}$の微分の離散化方法によっては、数値解が異なることがあります。異なると言っても、通常は流体のナビエストークスには流体粘性ので不連続解を分散させて解が振動しないようにしますし、不連続な解が出ることも稀なのでどのような離散化手法をとってもあまり解が変わりません。
ただ、衝撃波が出ると速度や圧力の不連続解が生じ、さらに粘性項より対流項が大きくなるので上記に近い方程式になります。
離散化スキームを以下のようにざっくり分けて特徴をまとめておきます。
upwind_difference.pdf (xrea.com)
- 1次精度:風上差分(upwind)→こちらは安定だが解が拡散してしまう
- 2次精度:中心差分、QUICK→こちらは不連続解をシャープにとらえようとするが、数値振動が起こりやすい
- TVDスキーム:minmod、vanLeer、vanAlbada、superBeeが有名。
色々な種類がありますが、不連続部分で振動を抑えるようにしながら、解はシャープにとらえようとするいい感じのスキーム
離散化スキームの種類はむちゃくちゃありますので、まずはこれくらいざっくりわけて特徴を理解しておくとよいでしょう。
- 対流項の発散スキームの比較
こちらはOpenFOAMの離散化スキームの比較として一番参考になる記事でしょう。 - Divergence scheme example
公式サイトにも離散化スキームに対する検討がされています。メッシュと離散化スキームの選択次第で結果がずいぶんと変わるのがわかるでしょう。 - OpenFOAM6.2 Numerical schemes
- OpenFOAM Basic Training
- 第1回オープンCAE講習会 OpenFOAM初中級講習B
- upwind_difference.pdf (xrea.com)
こちらのpdfはスキームについてよくまとめられています。
- OpenFOAMの移流方程式を使って離散化スキームの基礎的な内容を理解したい方
- OpenFOAMのチュートリアルから独自に検証するケースファイルを作りたい方
離散化スキームについて勉強したい方の参考になれば幸いです。
OpenFOAM-v2012(WSL2)
Python3.8.10(jupyter lab)
モデルの入手
移流方程式のモデルは前回の記事で作成しましたのでそちらをご参考ください。
サンプルモデルも用意したのでご利用ください。
- 【OpenFOAM】移流方程式で離散化スキームの勉強をする
- モデル入手[追記]※最終モデルをgithubにアップしました。
フォルダ構成
フォルダ構成は以下のようになっています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
├── main.py ├── orgCase │ ├── 0 │ │ ├── T │ │ └── U │ ├── Allrun │ ├── constant │ │ ├── polyMesh │ │ │ ├── boundary │ │ │ ├── faces │ │ │ ├── neighbour │ │ │ ├── owner │ │ │ └── points │ │ └── transportProperties │ ├── post.foam │ └── system │ ├── blockMeshDict │ ├── controlDict │ ├── fvSchemes │ ├── fvSolution │ ├── sampleDict │ └── setFieldsDict ├── resultDir └── schemeTest |
- orgCase:元のケースファイル
- schemeTest:スキームの一覧
- Allrun:計算実行スクリプト
- main.py:計算の自動実行スクリプト
ひとつずつ解説していきます。
orgCase:元のケースファイル
こちらはスキームを変えて実行するための元になるケースファイルです。
これをコピーしてスキームを変えていくというのを行います。
scalarTransportFoamは以下の偏微分方程式を解く非定常のソルバーです。
\frac{\partial T}{\partial t}+\nabla\cdot(\boldsymbol{u}T)-\nabla\cdot (D_{T}\nabla T)=\boldsymbol{S}_{T}\tag{1}
\end{align*}
本記事では(1)を少し簡単にするために、
- 生成項を0:$\boldsymbol{S}_{T}=0$
- 拡散項を0:$D_{T}=0$
- 流速は一定:$\boldsymbol{u}=(0.1, 0, 0)$
と設定するようにします。
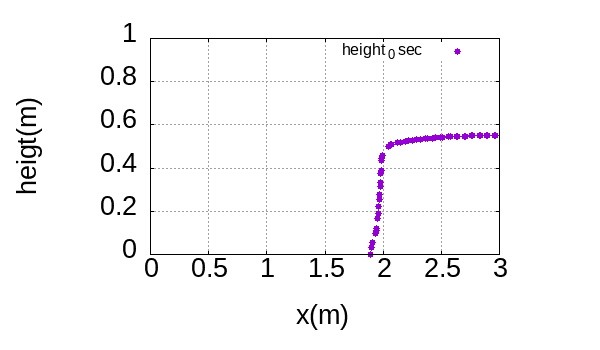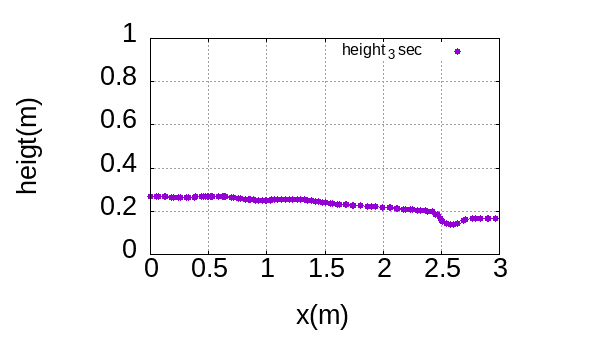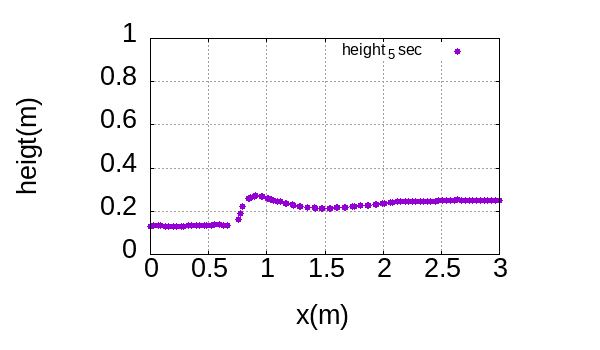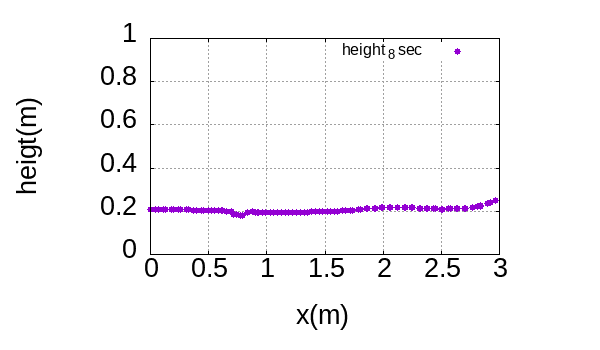
初期状態は以下のようになっています。
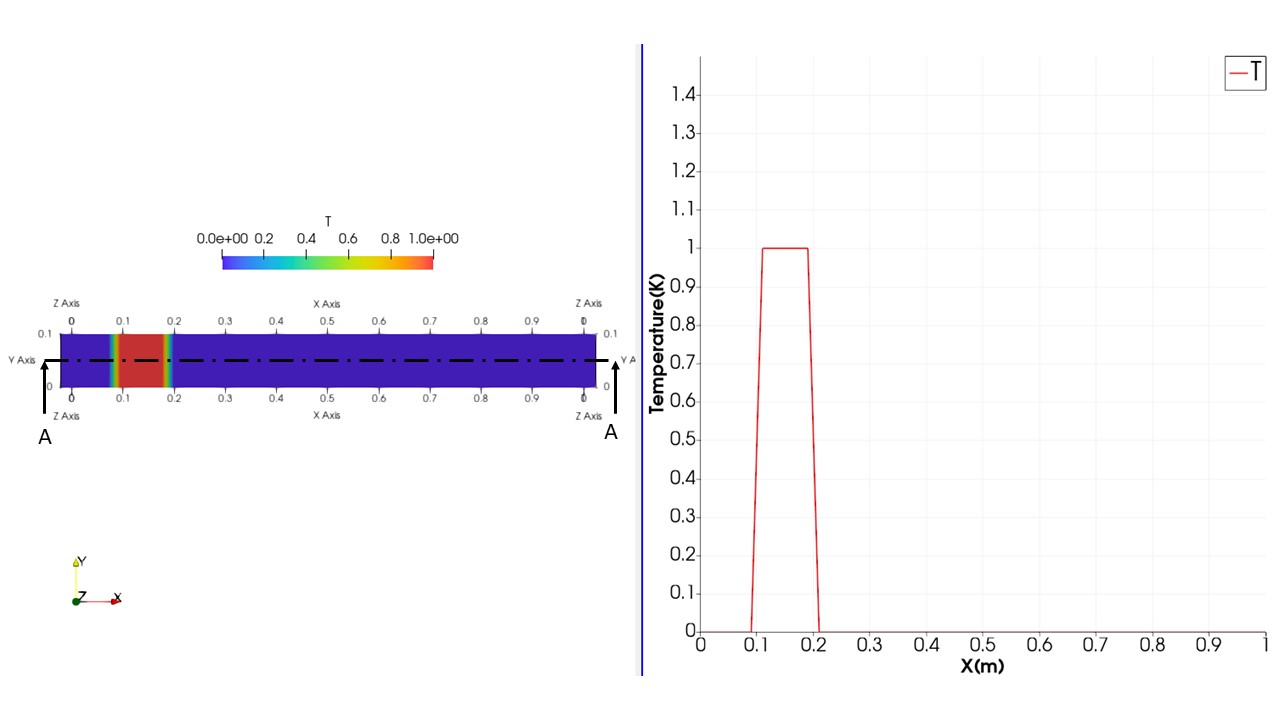
schemeTest:スキームの一覧
schemeTestというファイルにスキームの一覧を記載します。
schemeTest
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
linear upwind linearUpwind grad(T) QUICK limitedLinear 0.2 limitedLinear 1.0 vanLeer midPoint Minmod MUSCL LUST grad(T) SFCD SuperBee UMIST |
これをケースファイルの「system/fvSchemes」の「divSchemes」を変えていきます。
system/fvSchemes
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: v2012 | | \\ / A nd | Website: www.openfoam.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvSchemes; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // ddtSchemes { default Euler; } gradSchemes { default Gauss linear; } //ここを変える divSchemes { default none; div(phi,T) Gauss upwind grad(T); } laplacianSchemes { default none; laplacian(DT,T) Gauss linear corrected; } interpolationSchemes { default linear; } snGradSchemes { default corrected; } // ************************************************************************* // |
Allrun:計算実行スクリプト
計算を実行するためのスクリプトを作成します。
Allrun
|
1 2 3 4 5 6 7 |
#!/bin/sh cd "${0%/*}" || exit # Run from this directory . ${WM_PROJECT_DIR:?}/bin/tools/RunFunctions # Tutorial run functions #------------------------------------------------------------------------------ runApplication $(getApplication) #------------------------------------------------------------------------------ |
OpenFOAMが用意しているスクリプトの「RunFunctions」には便利な関数が用意されているので利用すると良いでしょう。
例えば、「runApplication $(getApplication)」と書くと計算させたソルバを実行しながらlogファイルも作成してくれます。
main.py:計算の自動実行スクリプト
計算実行のパラメータスタディを行う前にまずはやりたいことを整理した方が良いでしょう。
構成を考える
- スキームの一覧ファイルを作成
- baseをコピーする
- スキームを入れ替える
- Allrunスクリプトを実行する(postProcess)
- グラフにまとめる
- 全部のグラフを2列ずつにしてまとめる
jupyter labでデバッグしながら数でまとめられるものはまとめてしまい、mainのプログラの記述を少なくするようにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 |
from pathlib import Path import shutil import subprocess import numpy as np from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile import matplotlib.pyplot as plt import os # スキームファイルを読み込む def open_SchemeList(): with open('./schemeTest') as f: scheme_list = [s.strip() for s in f.readlines()] return scheme_list # baseをコピーする def clone_file(orgCase, resultDir): "orgCaseをresultDirに重複しないようにコピー" baseName = Path(orgCase).name addName = None if addName!=None: baseName += f'_{addName}' Path(resultDir).mkdir(exist_ok=True, parents=True) n=0 newCase = Path(resultDir) / f'{baseName}_{n}' while newCase.is_dir(): n += 1 newCase = Path(resultDir) / f'{baseName}_{n}' shutil.copytree(orgCase, newCase) return newCase # スキームを入れ替える def new_parameter(newScheme, newCase): fileScheme = ParsedParameterFile(newCase / 'system/fvSchemes') fileScheme.content['divSchemes'] fileScheme.content['divSchemes']['div(phi,T)'] = f'Gauss {newScheme}' fileScheme.writeFile() # Allrunスクリプトを実行する(postProcess) def Allrun(newCase): "Allrunを実行" out_run = subprocess.check_output(['./Allrun'], cwd=newCase) return out_run.decode() # グラフにする def graph(scheme, newCase, resultDir): time_list = os.listdir(Path(newCase) / f'postProcessing/samples') plt.figure() for time in time_list[::7]: temp_data = np.loadtxt(Path(newCase) / f'postProcessing/samples/{time}/x_T_T.xy').T plt.plot(temp_data[0], temp_data[1],label=f'time = {time}') plt.legend() plt.grid() plt.yticks(np.arange(-0.5,2,0.25)) plt.xlabel("X(m)", fontsize=12) plt.ylabel("Temperature(K)", fontsize=12) plt.title(f"Temperature Advection Equation({scheme})", fontsize=16) # 画像賦存用データのフォルダ作成 result_graph_dir = Path(resultDir)/'savefig' if(os.path.isdir(result_graph_dir) == False): os.mkdir(result_graph_dir) # グラフを保存 plt.savefig(f'{result_graph_dir}/{scheme}.png') plt.close() # 全部のグラフを2列ずつにしてまとめる def Allgraph_png(scheme_list): fig = plt.figure(figsize = (12,24)) for i, scheme in enumerate(scheme_list): #グラフを表示する領域を,figオブジェクトとして作成. col = len(scheme_list)//2 + 1 ax1 = fig.add_subplot(col,2,i+1) time_list = os.listdir(f'./resultDir/orgCase_{i}/postProcessing/samples') for time in time_list[::7]: temp_data = np.loadtxt(f'./resultDir/orgCase_{i}/postProcessing/samples/{time}/x_T_T.xy').T ax1.plot(temp_data[0], temp_data[1],label=f'time = {time}') ax1.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=8) plt.subplots_adjust(wspace=0.8, hspace=0.8) ax1.grid() ax1.set_yticks(np.arange(-0.5,2,0.25)) ax1.set_xlabel("X(m)", fontsize=12) ax1.set_ylabel("Temperature(K)", fontsize=12) ax1.set_title(f"Temperature Advection Equation({scheme})", fontsize=12) # グラフを保存 fig.savefig('./graph_Allschemes.png') plt.close() #================== main ======================== orgCase = 'orgCase' resultDir = 'resultDir' # スキームのリスト scheme_list = open_SchemeList() print(f'スキームの数 : {len(scheme_list)}') # 計算実行 for i, scheme in enumerate(scheme_list): print(f'{i+1} ======== {scheme} =========') newCase = clone_file(orgCase, resultDir) # 関数を実行する new_parameter(scheme, newCase) # スキームを入れ替える Allrun(newCase) # 計算を実行 graph(scheme, newCase, resultDir) # グラフ化 # 全てのグラフをまとめる Allgraph_png(scheme_list) |
結果はスキームごとに分けて「resultDir/savefig」に画像を作成し保存、全てのスキームでの結果を「graph_AllShemes.png」に画像を作成し保存しています。
pythonを実行します。
|
1 |
python3 main.py |
以下のように計算が進みます。
|
1 2 3 4 5 6 7 8 9 |
スキームの数 : 14 1 ======== linear ========= 2 ======== upwind ========= 3 ======== linearUpwind grad(T) ========= 4 ======== QUICK ========= 5 ======== limitedLinear 0.2 ========= 6 ======== limitedLinear 1.0 ========= 7 ======== vanLeer ========= (以下省略) |
※WSLでplt.figure()などグラフ表示でエラーが出る場合は「export DISPLAY:=1.0」とするとエラーがなくなります。
結果を確認
結果は「resultDir/savefig」に画像として保存するようにしています。
例えばスキーム「linear(中心差分)」の結果は以下のようになります。
ぐちゃぐちゃですね。
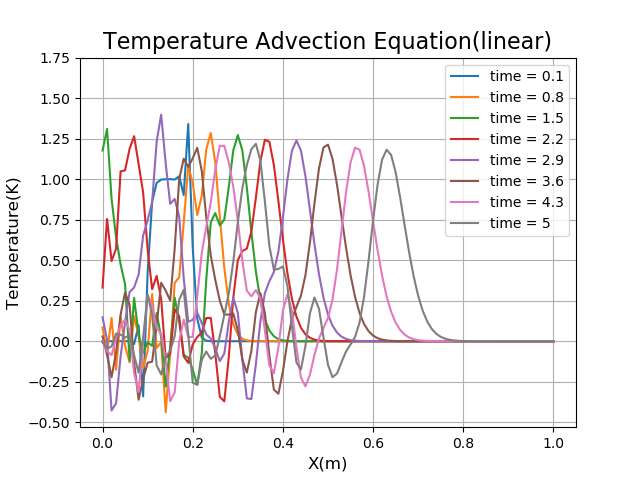
例えばスキーム「upwind(風上差分)」の結果は以下のようになります。
安定していますが、拡散しています。
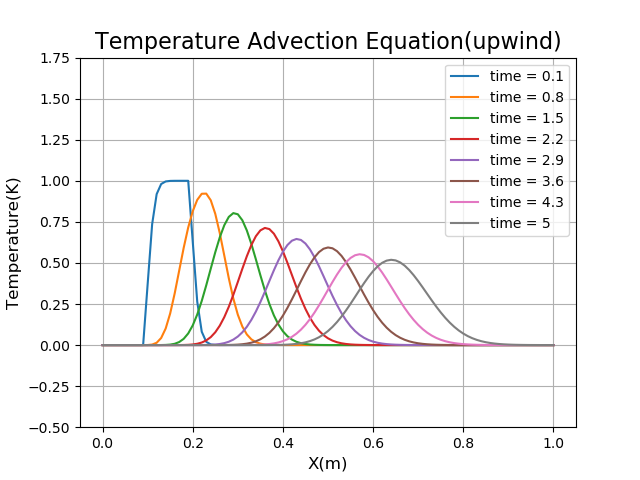
全てのスキームをまとめたものが「graph_AllShemes.png」です。
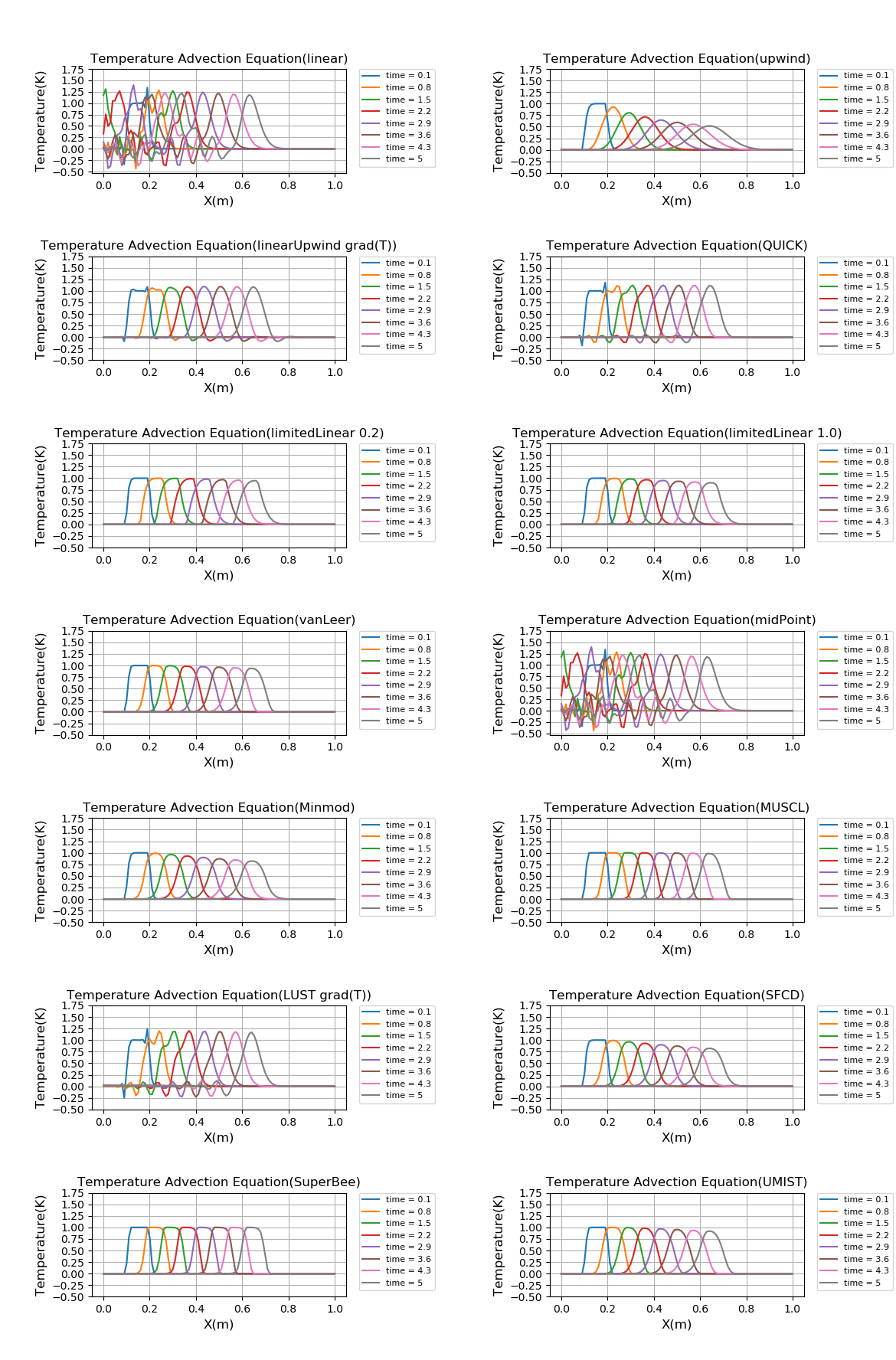
スキームは有名で実装が容易なものから聞いたことないものまで色々あります。
例えば以下のツイートのようなスキームは勉強不足で初めて聞きました💦
移流方程式みたいな簡単なやつでもどういうスキームならどういう結果になるのかあまり確認したことなく確認している。
TVDスキームのSuperBee?
これが拡散しにくい? pic.twitter.com/0ZqJPXs2jg— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) February 15, 2023
まとめ
スキームは試して結果を眺めてみないとわからないので、本記事のような簡単な移流方程式で色々と試してみました。
計算時間まではまとることをしていませんが、スキームによって計算時間に差が出るみたいなのでそちらも比較しても良いかもしれません。
Pythonの自動スクリプトなども参考になれば幸いです。
参考書
有限体積法の勉強にはこの本で間違いないです。
対流項目が中心差分で安定しないことを理論的に評価しておりとても参考になります。
有限体積法の詳しい解説として英語ですが以下の書籍を挙げておきます。
OpenFOAMに沿った解説もされているのでOpenFOAMを勉強する人にとっては有用です。
OpenFOAMの基本的な設定を学ぶことができる書籍として以下の参考書がお勧めです。
本書はESI版ではなくFoundation版でありOpenFOAMv2.xで書かれたやや古い内容です。その点に注意してESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
OpenFOAM全般の設定などまとめられた書籍として以下のものがあります。
こちらもFoundation版なので、ESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
こちらのオープンCAE学会から技術書典にOpenFOAMでメッシュ作成【PDF版】が出ています。難しい内容ではありますが、OpenFOAMのメッシュに関する内容が1000円で学べます。