こんにちは（@t_kun_kamakiri）
本記事はOpenFOAMでの粒子追跡の備忘録です。
自分で理解したことや試したことをまとめていきます。
前回の記事では「icoUncoupledKinematicParcelFoamを使って粒子追跡の解析」をとりあえず試しに使ってみました。
- icoUncoupledKinematicParcelFoamを使って粒子追跡の解析
- 流体は一定の速度、粒子は球体形状とし流体の力を受けて運動する様子をシミュレーション
- 質点の運動理論とOpenFOAMの結果を比較する
球体にはたらく重力と抗力による質点の運動とOpenFOAMのicoUncoupledKinematicParcelFoamを使って得られた粒子の運動を比較を行うことでOpenFOAMの中身を理解しようという試みです。OpenFOAMの結果は厳密には壁との摩擦もありますし質点ではないので、質点と考えた場合の運動とずれが生じます。
OpenFOAMv2012(EDI版)
WSL2
粒子の設定
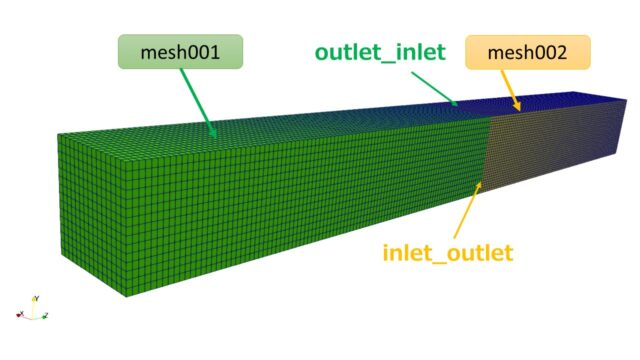
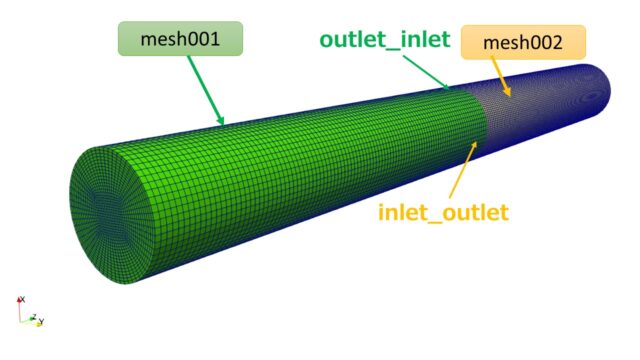
モデル作成は前回の記事で解説を行っています。
粒子の設定は「constant/kinematicCloudProperties」で行います。
constant/kinematicCloudProperties
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 | solution { active true; coupled false; transient yes; cellValueSourceCorrection off; maxCo 0.3; sourceTerms { schemes { } } interpolationSchemes { rho cell; U cellPoint; mu cell; } integrationSchemes { U Euler; } } constantProperties { rho0 964; youngsModulus 6e8; poissonsRatio 0.35; } subModels { particleForces { sphereDrag; gravity; } injectionModels { model1 { type manualInjection; massTotal 0; parcelBasisType fixed; nParticle 1; SOI 0; positionsFile "kinematicCloudPositions"; U0 ( 0 0 0 ); sizeDistribution { type fixedValue; fixedValueDistribution { value 0.01; } } } } dispersionModel none; patchInteractionModel standardWallInteraction;//none; //patchInteractionModel localInteraction; localInteractionCoeffs { } surfaceFilmModel none; stochasticCollisionModel none; collisionModel pairCollision; pairCollisionCoeffs { // Maximum possible particle diameter expected at any time maxInteractionDistance 0.006; writeReferredParticleCloud no; pairModel pairSpringSliderDashpot; pairSpringSliderDashpotCoeffs { useEquivalentSize no; alpha 0.12; b 1.5; mu 1.0; cohesionEnergyDensity 0; collisionResolutionSteps 12; }; wallModel wallLocalSpringSliderDashpot; wallLocalSpringSliderDashpotCoeffs { useEquivalentSize no; collisionResolutionSteps 12; walls { youngsModulus 1e10; poissonsRatio 0.23; alpha 0.12; b 1.5; mu 1.0; cohesionEnergyDensity 0; } }; } standardWallInteractionCoeffs { type rebound; e 1; mu 0; } } cloudFunctions {} |
前回の記事での設定を以下に変えました。
1 2 3 4 5 6 7 8 | patchInteractionModel standardWallInteraction; standardWallInteractionCoeffs { type rebound; e 1; mu 0; } |
これで壁との反発係数が1になったのかな？
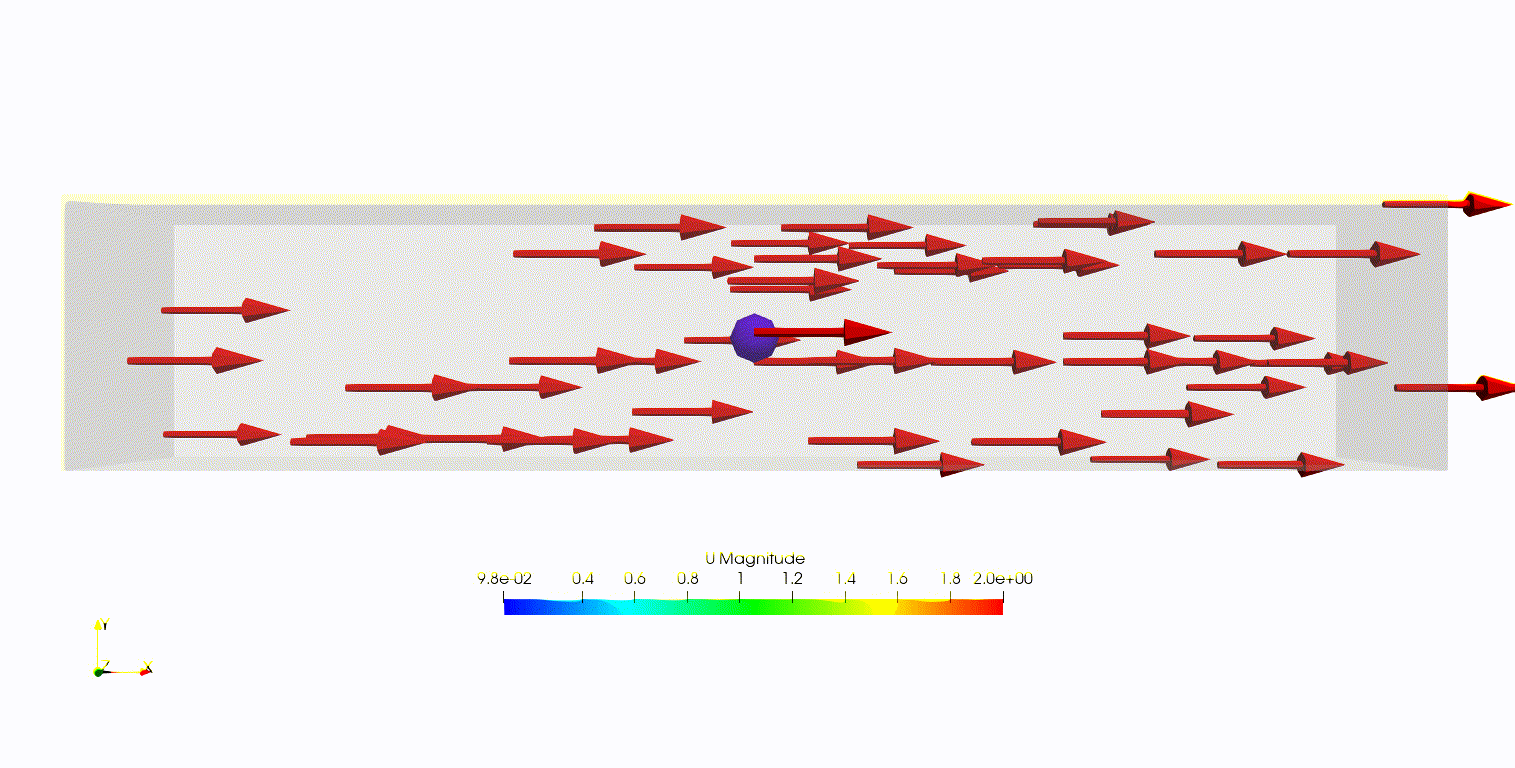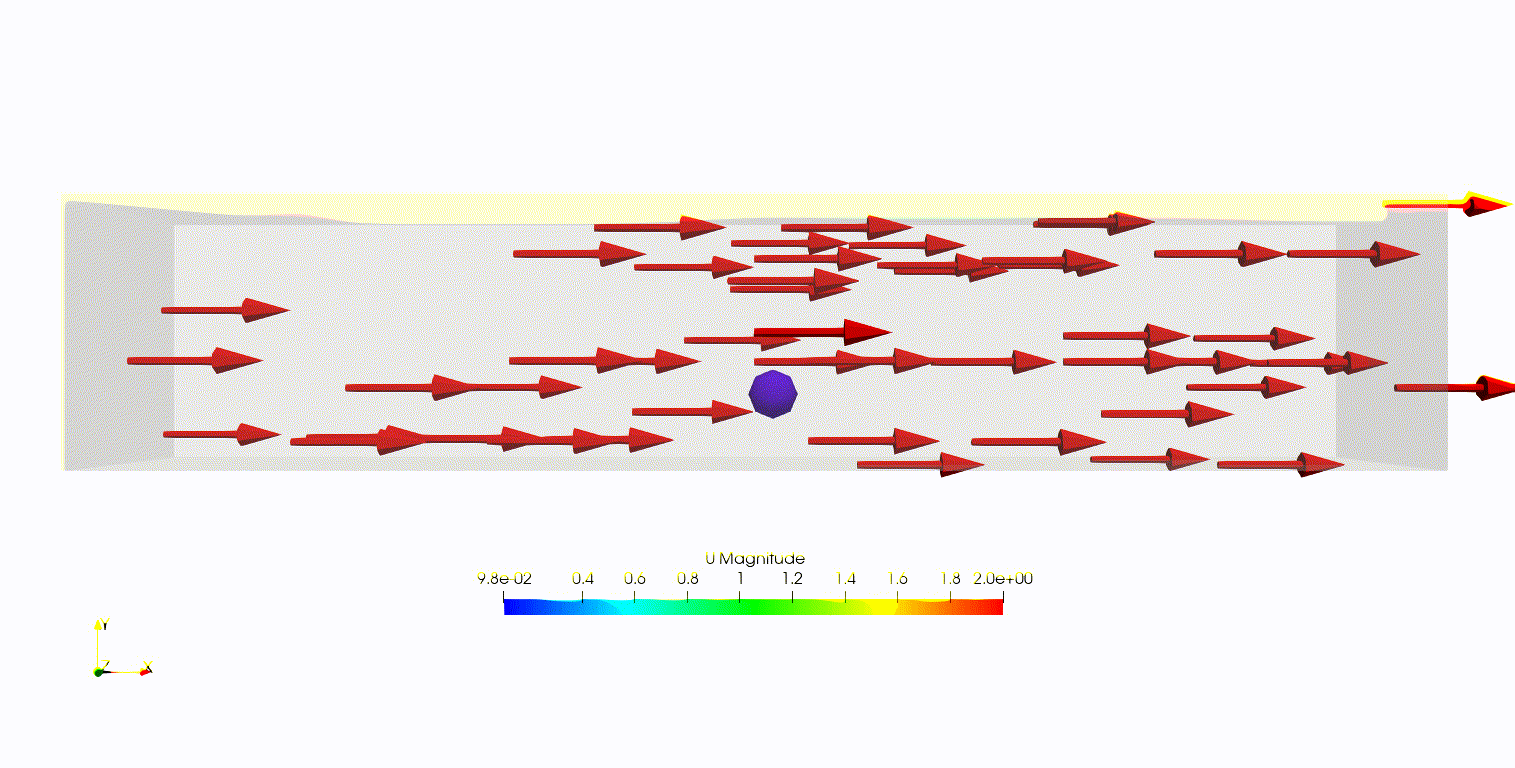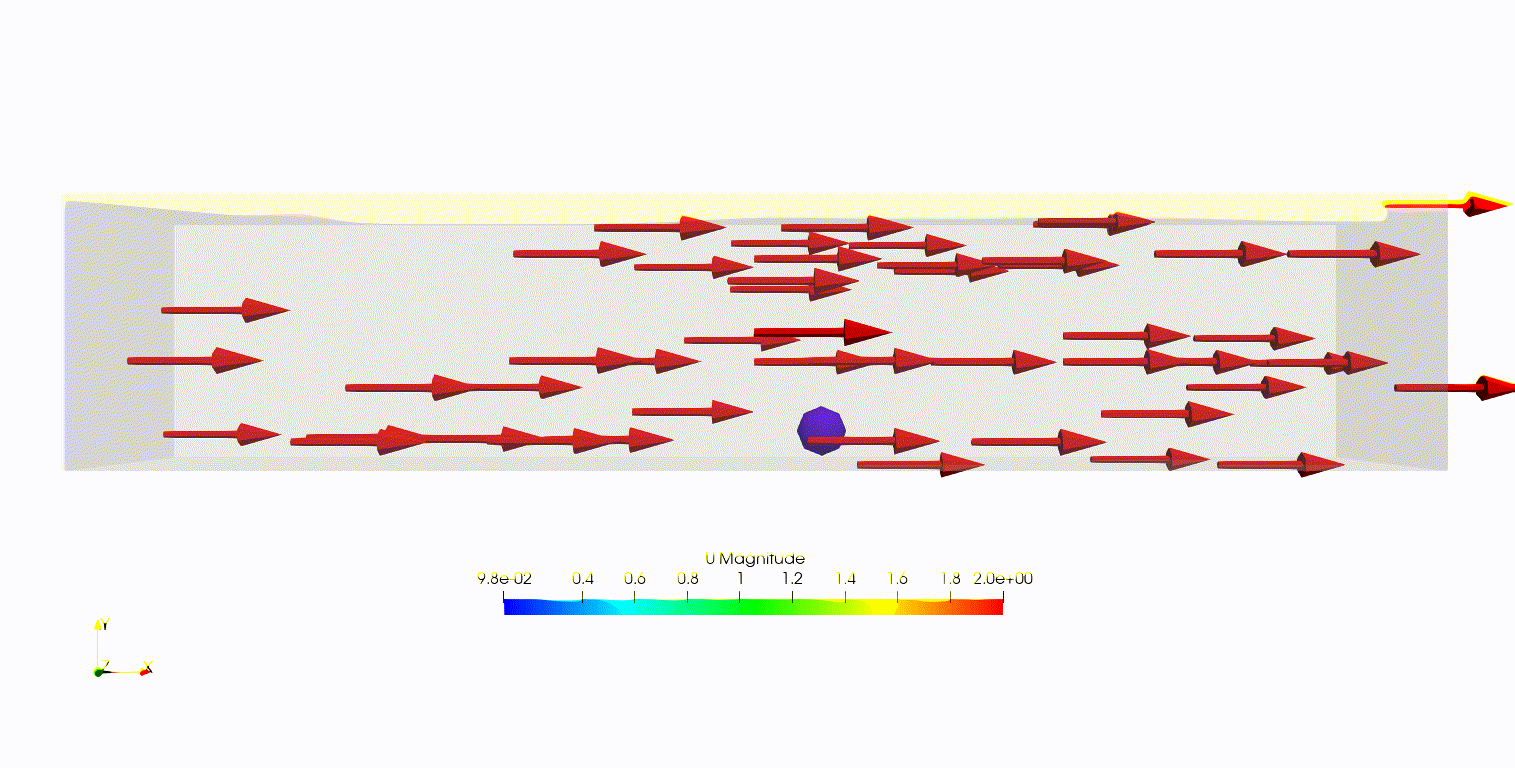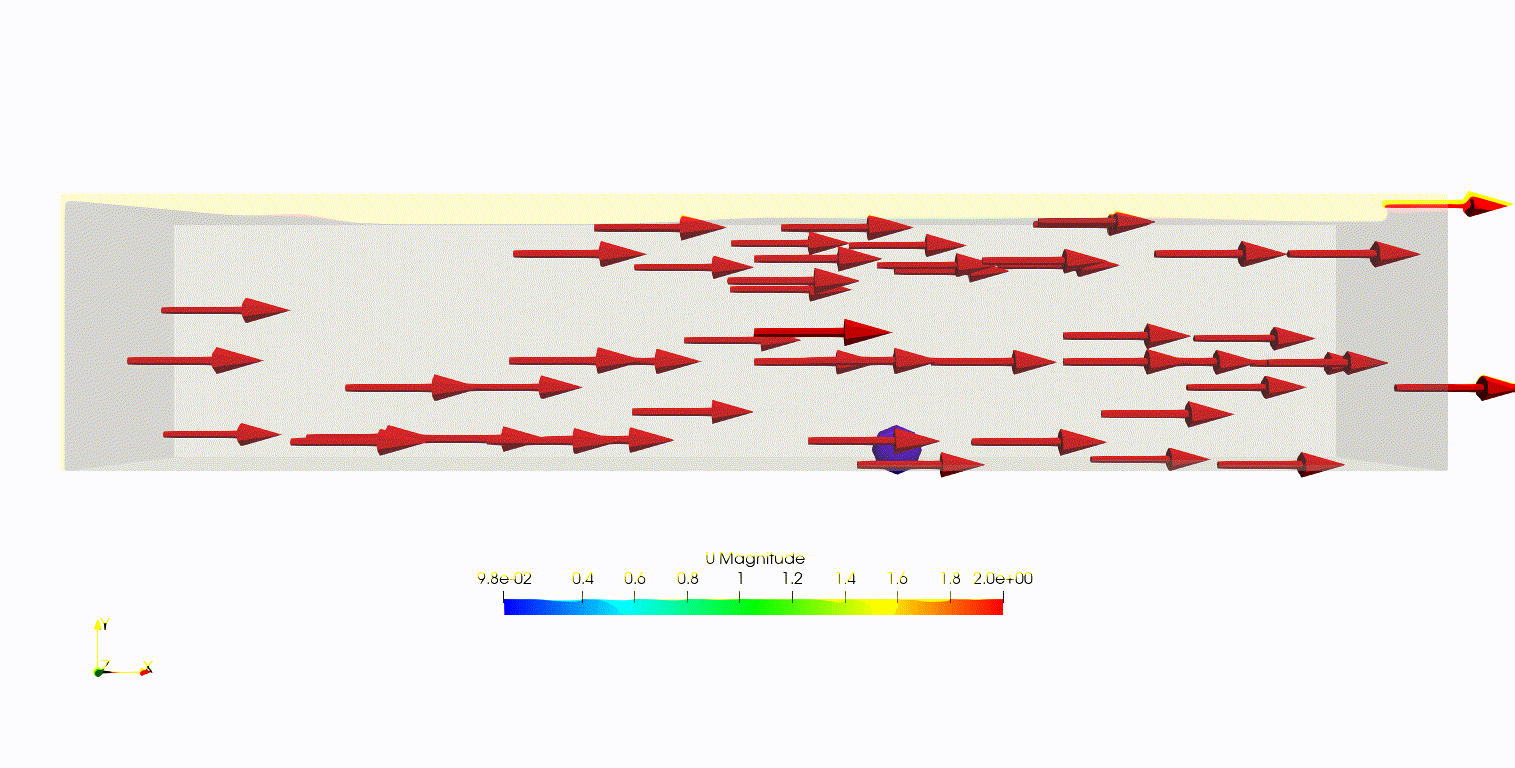
理論式
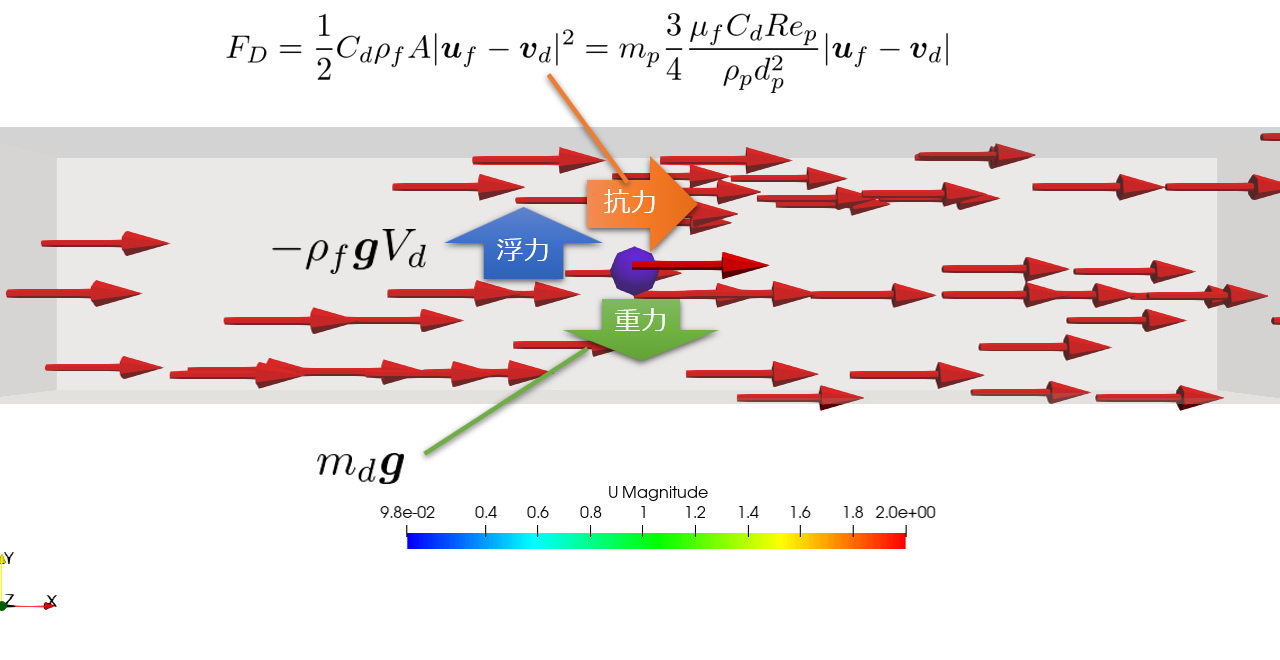
粒子には以下の力がはたらきます。
- 抗力
- 重力
- 浮力
- 地面との反発力
- 地面との摩擦力
※揚力は今回はシミュレーションに入れていません。
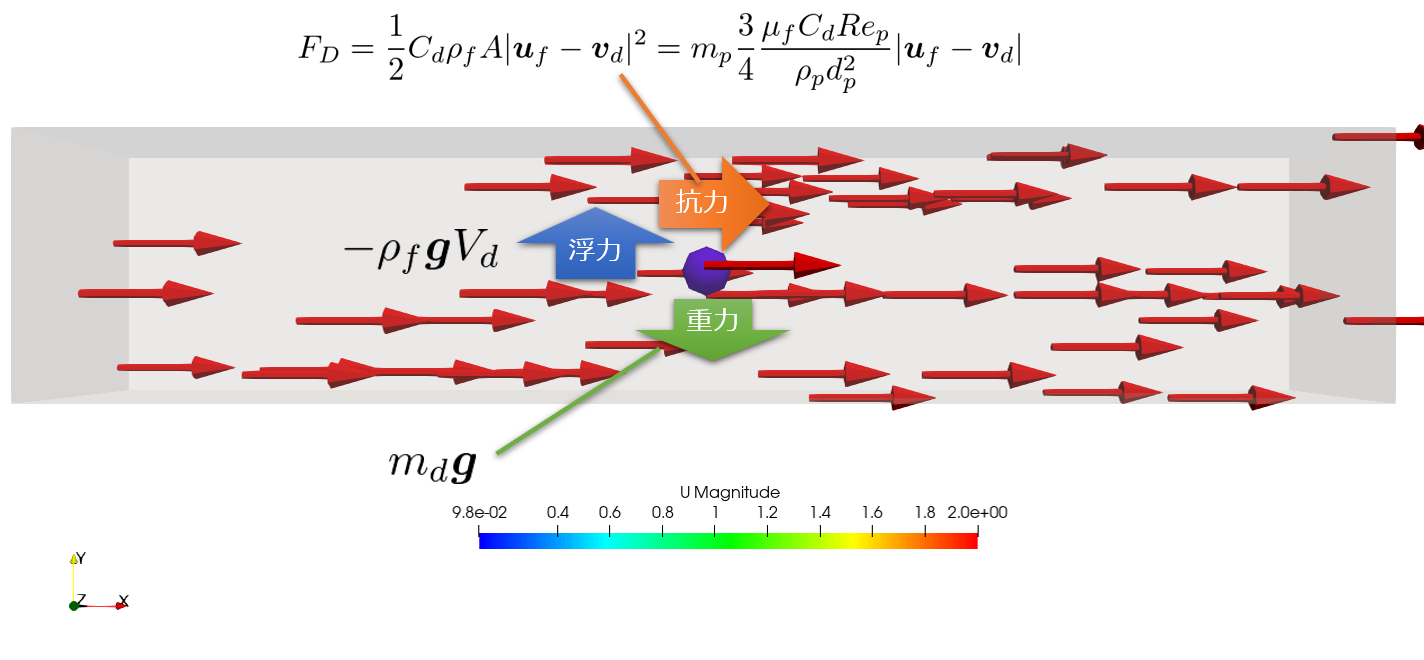
抗力について
\boldsymbol{F_{D}}&=\frac{1}{2}C_{d}\rho_{f}A|\boldsymbol{u}_{f}-\boldsymbol{v}_{d}|^2\\
&=m_{p}\frac{3}{4}\frac{\mu_{f}C_{d}Re_{p}}{\rho_{p}d_{p}^2}|\boldsymbol{u}_{f}-\boldsymbol{v}_{d}|\tag{1}
\end{align*}
- $\mu_{f}=1e^{-05}$ : 流体の粘性係数
- $\boldsymbol{u}_{f}$：流体の速度
- $\boldsymbol{v}_{d}$：粒子の速度
- $d_{p}=10$[mm] $=0.01$[m]
- $\rho_{d} = 964$[kg/m3] : 粒子の密度
- $Re_{p}=\frac{|\boldsymbol{u}-\boldsymbol{v}|d_{p}}{\mu_{f}/\rho}$ : レイノルズ数
- $F_{D}=\frac{1}{2}C_{d}\rho_{f}A|\boldsymbol{u}_{f}-\boldsymbol{v}_{d}|^2=m_{p}\frac{3}{4}\frac{\mu_{f}C_{d}Re_{p}}{\rho_{p}d_{p}^2}|\boldsymbol{u}_{f}-\boldsymbol{v}_{d}|$：抗力
- $A=\pi\big(\frac{d_{p}}{2}\big)^2$
SphereDragForce.C
1 2 3 4 5 6 7 8 9 10 11 | template<class CloudType> Foam::scalar Foam::SphereDragForce<CloudType>::CdRe(const scalar Re) const { // (AOB:Eq. 35) if (Re > 1000.0) { return 0.424*Re; } return 24.0*(1.0 + (1.0/6.0)*pow(Re, 2.0/3.0)); } |
球体の抗力はレイノルズ数と関係性があります。
※以下は以前にOpenFOAMで比較したものです。
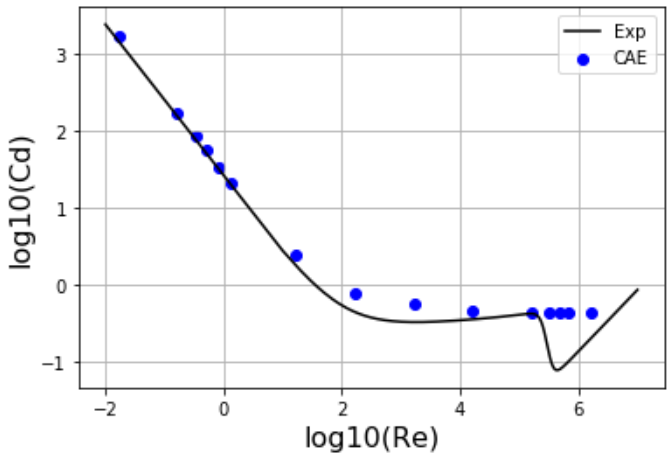
レイノルズ数は$R_{e}=1000$で場合分けしています。
抗力は以下の理論式で記述しています。
C_{d}=\left\{\begin{matrix}
\frac{24}{Re}\big(1.0 + \frac{1}{6}Re^{2/3}\big)&(Re\leq 1000)\\
0.424 &(Re>1000)
\end{matrix}\right.\tag{2}
\end{align*}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | template<class CloudType> Foam::forceSuSp Foam::SphereDragForce<CloudType>::calcCoupled ( const typename CloudType::parcelType& p, const typename CloudType::parcelType::trackingData& td, const scalar dt, const scalar mass, const scalar Re, const scalar muc ) const { // (AOB:Eq. 34) return forceSuSp(Zero, mass*0.75*muc*CdRe(Re)/(p.rho()*sqr(p.d()))); } |
重力と浮力について
\boldsymbol{F_{g}}&=m_{d}\boldsymbol{g}-\rho_{f}\boldsymbol{g}V_{d}\\
&=m_{d}\boldsymbol{g}\bigg(1-\frac{\rho_{f}}{\rho_{d}}\bigg)\tag{3}
\end{align*}
重力と浮力はひとつにまとめることができます。
GravityForce.C
1 2 3 4 5 6 | template<class CloudType> Foam::GravityForce<CloudType>::GravityForce(const GravityForce& gf) : ParticleForce<CloudType>(gf), g_(gf.g_) {} |
重力を定義し、
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | template<class CloudType> Foam::forceSuSp Foam::GravityForce<CloudType>::calcNonCoupled ( const typename CloudType::parcelType& p, const typename CloudType::parcelType::trackingData& td, const scalar dt, const scalar mass, const scalar Re, const scalar muc ) const { forceSuSp value(Zero); value.Su() = mass*g_*(1.0 - td.rhoc()/p.rho()); return value; } |
地面との反発力については以下StandardWallInteraction.Cで確認すれば良いですが難しそうだったので理解するのは保留にしました。
OpenFOAMと理論式を比較
- $y$方向は重力と浮力
- $x$方向は抗力
$y$方向について（重力と浮力）
$y$方向は重力（+浮力）と地面と反発した際の反発係数を適当に調整して以下のように記述できます。
y=-\frac{1}{2}g(t-t_n)^2+e^{n}v_{y}(t-t_n)+h\tag{4}
\end{align*}
理論式でe=0.83にするとそれっぽくなりました。
$x$方向について（抗力）
$x$方向はレイノルズ数が$Re=2000$くらいなので抗力係数が$C_{d}=0.424$として良いでしょう。
また、流体速度が$u=2$[m/s]で粒子の速度は1秒までの計算で$v=0~0.1$の間なので、レイノルズ数はほぼ流体速度の一定値$u=2$[m/s]で決まると言ってよいでしょう。
ゆえに抗力も定数になるので、運動方程式から以下のように$x$方向の式が立ちます。
x = \frac{1}{2}\frac{F_D}{m}t^2+x_{0}\tag{5}
\end{align*}
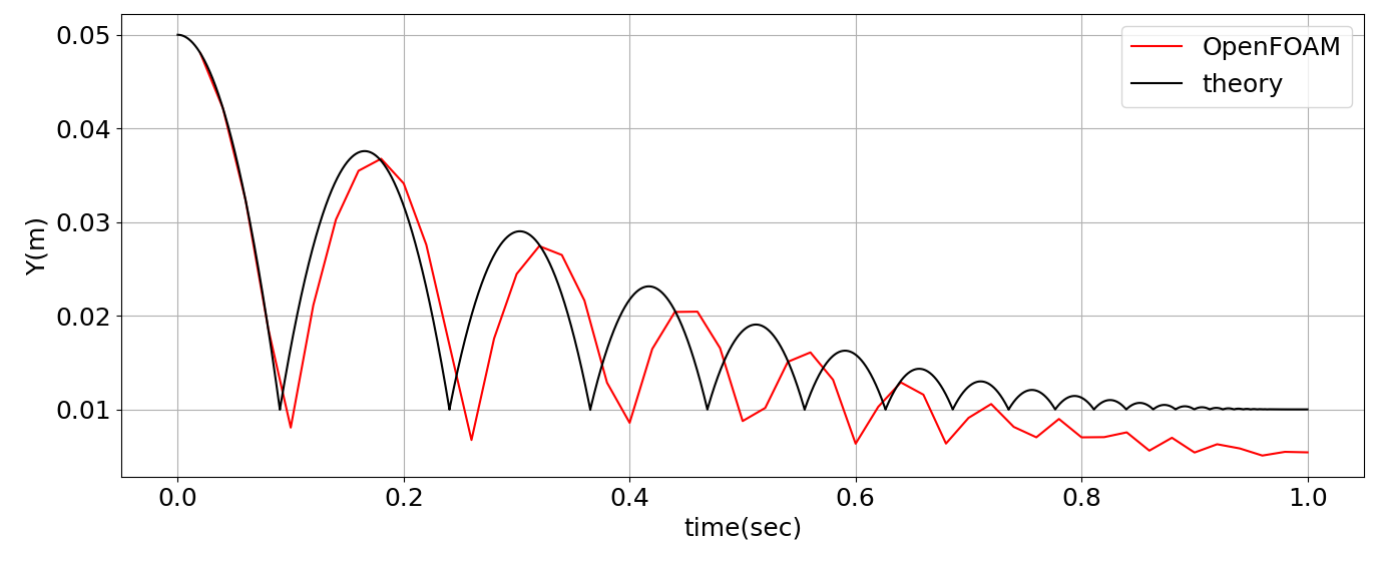
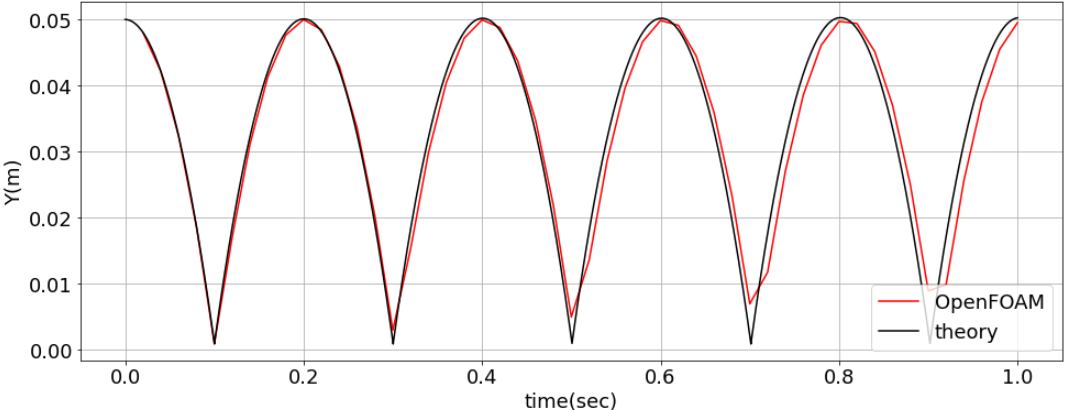
地面と接するまでは一致していますが、やはり地面と接触して以降は徐々にずれてきます。これは理論式が地面との摩擦力を考慮していないからだろう？と考えていますが・・・・自分の理解が進んだらアップデートします。
モデルを修正
地面との反発係数が正しいのかを再度確認するために、流体からの抗力の設定を無くし重力のみの設定に変更します。
また地面との衝突は「 patchInteractionModel standardWallInteraction;」を効かすために「collisionModel none;」としておきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | subModels { particleForces { //sphereDrag; gravity; } (省略) collisionModel none;//pairCollision; patchInteractionModel standardWallInteraction;//none; standardWallInteractionCoeffs { type rebound; e 1; mu 0; } } |
これで地面との反発係数が１になる計算ができたようです。
ただし地面との距離が球体の直径に応じて反発していると思ったのですがどうも関係ないようです・・・詳細はソースコードStandardWallInteraction.Cを確認すれば良いかもしれません。軽く確認したところ粒子の直径に応じて地面との接触を感知しているようには見えませんでした。あくまで粒子は質点として跳ね返り位置を決めているのか？だとすると粒子の跳ね返り位置はメッシュサイズに依存する気がします。
ちなみに粒子の直径を変えても粒子の座標の軌跡は変わりませんでした。
あとは浮力の影響かもしれません。OpenFOAMでgravityを設定すると$\boldsymbol{F_{g}}=m_{d}\boldsymbol{g}-\rho_{f}\boldsymbol{g}V_{d}=m_{d}\boldsymbol{g}\bigg(1-\frac{\rho_{f}}{\rho_{d}}\bigg)$のように重力と浮力一緒にして計算しているようです。
あと気になるのは、OpenFOAMの結果は跳ね返り位置がだんだん高くなっています。出力した座標値を拾っているからなんでしょうか。
理論計算は「ymin = 0.001」で地面から跳ね返るという計算にして重ねてみました。
まとめ
本記事はicoUncoupledKinematicParcelFoamソルバを使った粒子追跡について解説しました。
球体にはたらく重力と抗力による質点の運動とOpenFOAMのicoUncoupledKinematicParcelFoamを使って得られた粒子の運動を比較してみましたが、自分の理解が足りていないので一致しませんでしたが、OpenFOAMの結果は厳密には壁との摩擦もありますし質点ではないので、質点と考えた場合の運動とずれが生じます。
シミュレーションだけしていては、内部でどのような計算が行われているかユーザはわからないのですが、本記事のような基本的な理解からはじめると少しずつ理解していきます。
理解が進んだらアップデートしたいですね。
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍が無い中唯一わかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
OpenFOAMコードの辞書的な扱いとしては以下の参考書が大変役に立ちます。
本記事ではESI版のOpenFOAMを使っているため本書のFoundation版で対応していない部分がありますが、その辺を考慮しても持っていて損はないでしょう。
Follow @t_kun_kamakiri