【熱伝導とは？】熱伝導方程式の導出

（@t_kun_kamakiri）

製品開発をしていると熱に関する問題に出くわすことが多いですよね。

当ブログでは伝熱工学の基礎的内容を以下のシリーズに分けて解説を行います。

伝熱工学の基礎

トップページ

今回は熱伝導について図を用いながらわかりやすく解説をします。
以下の内容について解説を行います。

フーリエの法則：温度差による熱移動の基礎的な法則
熱伝導方程式：温度分布の時間変化と空間変化の偏微分方程式

今回導くのは熱伝導方程式です。

熱伝導方程式

\begin{align*}
\frac{\partial T}{\partial t}=\alpha\bigg(\nabla^2 T+\frac{\dot{s}}{k}\bigg)
\end{align*}

前回の内容と被る部分もありますが、復習のつもりで読んでください。

こんな人にお勧め

工学系の学生
製造業に勤める技術者
技術士を目指している技術者

フーリエの法則
熱伝導方程式
熱伝導方程式の導出
まとめ
おすすめ参考書

フーリエの法則

熱伝導に関係する式には、単位面積・単位時間当たりの熱移動と単位長さあたりの温度差を熱伝導率という比例係数で結んだフーリエの法則があります。

フーリエの法則

\begin{align*}
\dot{q}=-k\frac{dT}{dx}\tag{1}
\end{align*}

熱伝導率：$k[W/m K]$

詳しくは前回の記事をご参考ください。

熱伝導方程式

(2)のフーリエの法則$\dot{q}=-k\frac{dT}{dx}$は温度勾配から熱伝導率という物体特有の係数を用いて熱流束を定義するものです。
フーリエの法則は空間的変化は表現できても時間的変化は考慮していない定常的な熱伝導の式です。

温度の空間変化に加えて時間的変化を考えるためには、時間微分の項を含んだ方程式を考える必要があります。
それが熱伝導方程式です。

熱伝導方程式

\begin{align*}
\frac{\partial T}{\partial t}=\frac{k}{c\rho}\bigg(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}+\frac{\partial^2 T}{\partial z^2}+\frac{\dot{s}}{k}\bigg)\tag{2}
\end{align*}

熱伝導率：$k[W/m K]$
熱容量：$c[J/kg K]$
密度：$\rho [kg/m^3]$

じゃっかんイカツイ感じの方程式ですが、導出方法と各項の意味を後ほど詳しく解説します。
補足になりますが、参考書では以下のように1次元で考えて、

\begin{align*}
\frac{\partial T}{\partial t}=\frac{k}{c\rho}\bigg(\frac{\partial^2 T}{\partial x^2}+\frac{\dot{s}}{k}\bigg)\tag{3}
\end{align*}

としている場合もあります。

また、熱源の項を0として

\begin{align*}
\frac{\partial T}{\partial t}=\frac{k}{c\rho}\frac{\partial^2 T}{\partial x^2}\tag{4}
\end{align*}

と書かれていることもあります。

さらに、$\alpha = \frac{k}{c\rho}$と置いて、

\begin{align*}
\frac{\partial T}{\partial t}=\alpha\frac{\partial^2 T}{\partial x^2}\tag{5}
\end{align*}

と書かれる場合もあります。
ここで$\alpha = \frac{k}{c\rho}[m^2/s]$を温度拡散係数と呼んで温度の広がりやすさの量を定義します。
(5)は1次元の熱伝導方程式と呼ばれるものですが、方程式の形は拡散方程式と同じなので、熱拡散方程式とも呼ばれます。

熱伝導方程式の導出

熱伝導方程式の導出には、以下のような考え方を導入します。

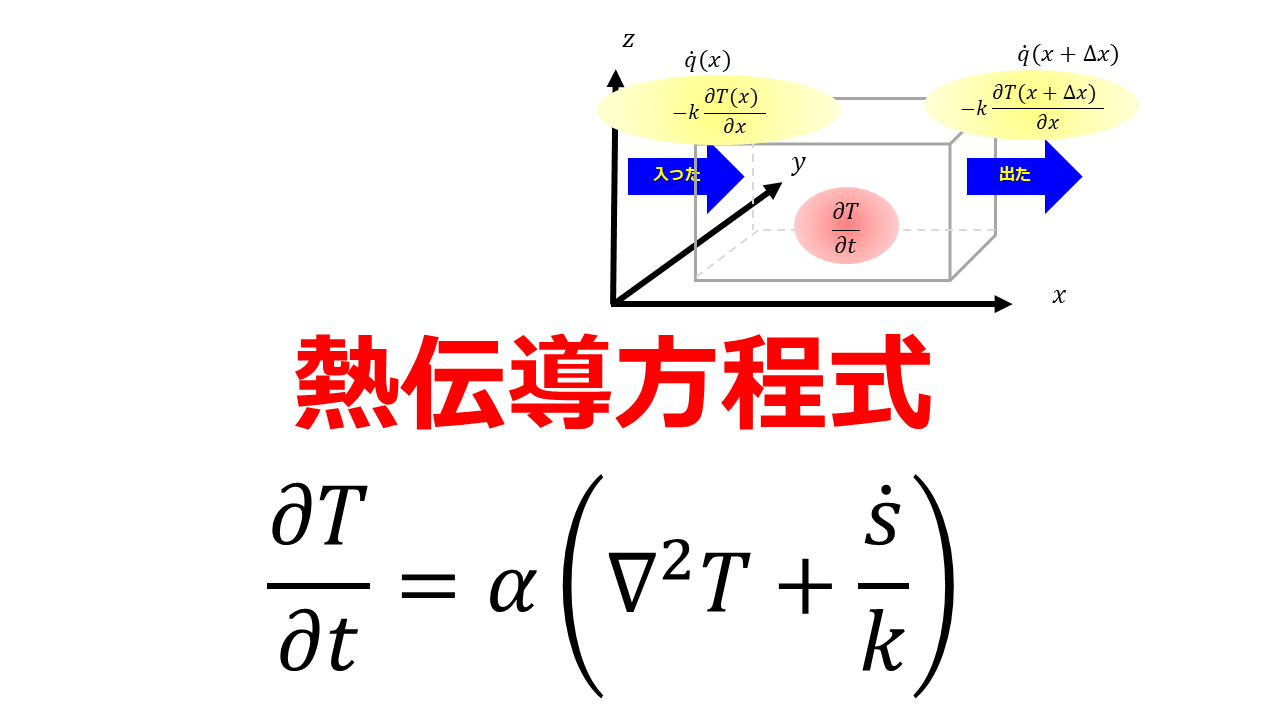
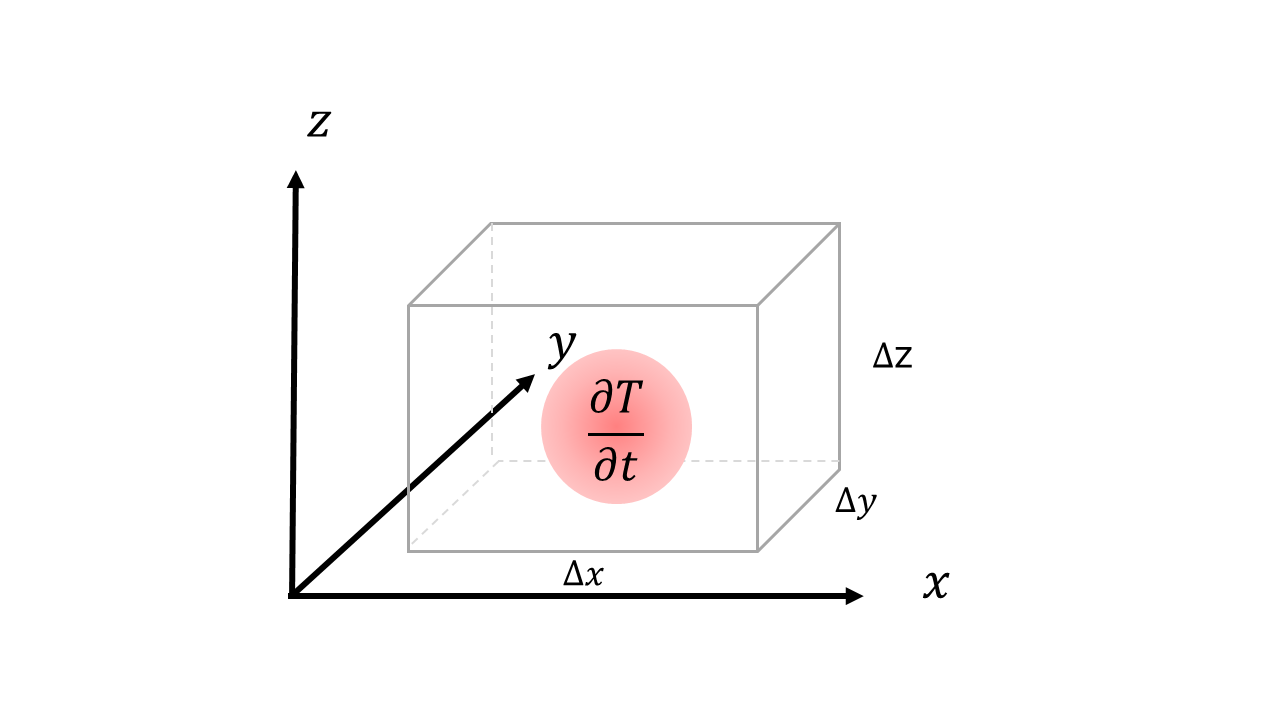
以下のような微小体積$\Delta x\Delta y\Delta z$について考えます。

体積内で時間的変化した熱量 = 空間的に出入りした正味の熱量 + 体積内の発熱量

言葉で説明すると「箱の中で1秒間あたりに変化した熱量は、1秒間に箱から出入りした熱量と発熱量に等しい」ということになります。

体積内で時間的変化した熱量

式はあくまで熱量（エネルギー）で計算しないといけないので、物体の比熱$c$[J/kg K]を使って単位時間あたりに変化した熱量を計算します。
入ってきた熱量を正になるため、時間変化量としては正となります。

\begin{align*}
\underset{質量 m}{\rho \Delta x\Delta y\Delta z}\times\underset{比熱 }{c}\times\underset{単位時間当たりの\\温度変化}{\frac{\Delta T}{\Delta t}}
\end{align*}

$\Delta T$と書くと温度差を意味しますが、極限を取って$\frac{\partial T}{\partial t}$と考えても良いです。

\begin{align*}
\rho c\frac{\partial T}{\partial t}\Delta x\Delta y\Delta z\tag{6}
\end{align*}

空間的に出入りした正味の熱量

出入りした熱量はフーリエの法則より求めます。
簡単に考えるために$x$方向のみの熱量の出入りを考えます。

まずは右側の面と左の面の位置、温度、熱量を確認します。
※熱量$\dot{Q}$とは、単位時間での熱量変化（移動）

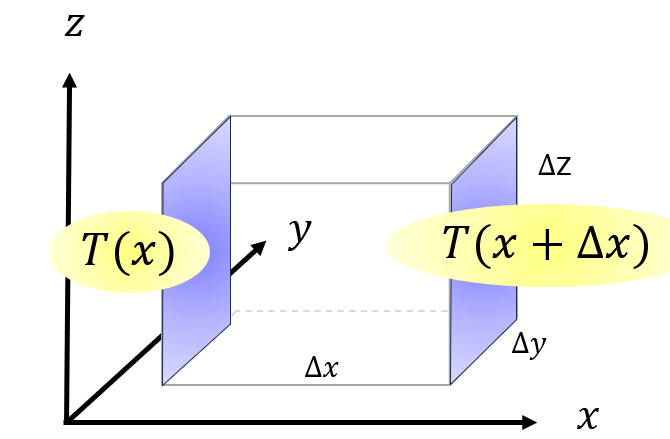
右の面：位置$\Delta x + x$での温度は$T(\Delta x + x)$、熱量は$\dot{Q}(\Delta x + x)$
左の面：位置$x$での温度は$T(x)$、熱流束は$\dot{Q}(x)$

入ってくる熱量を正の値、出ていく熱量を負の値とします。
熱量の移動はフーリエの法則を使うと、

右の面は熱が出ていくので$-\dot{Q}(\Delta x + x)\underset{フーリエ\\の法則}{=}-\big(-k\frac{\partial T(\Delta x + x)}{\partial x}\big)\Delta y\Delta z$、左の面は熱が入ってくるので$-\dot{Q}(x)\underset{フーリエ\\の法則}{=}-\big(-k\frac{\partial T(x)}{\partial x}\big)\Delta y\Delta z$となります。

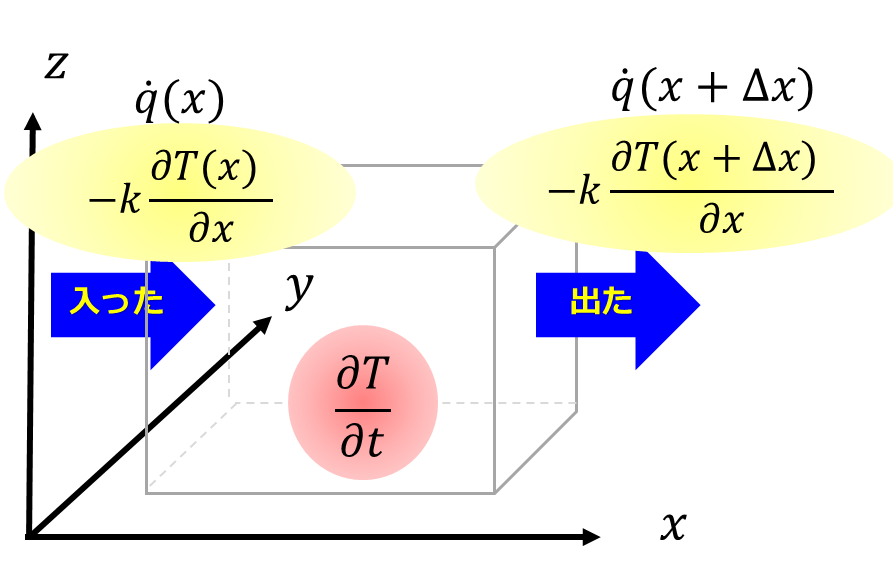
※面の面積が$\Delta y\Delta z$であるのをお忘れなく・・・

熱量だけ取り出して考えると、

\begin{align*}
-\dot{Q}(\Delta x + x)+\dot{Q}(x)=-\frac{\partial \dot{Q}}{\partial x}\Delta x
\end{align*}

となりますので、

\begin{align*}
-\frac{\partial }{\partial x}\bigg(-k\frac{\partial T}{\partial x}\bigg)\Delta x\Delta y\Delta z\tag{7}
\end{align*}

体積内の発熱量

発熱量は単位時間あたりに増加した量なので、以下のように書きます。

\begin{align*}
\dot{s}\Delta x\Delta y\Delta z\tag{8}
\end{align*}

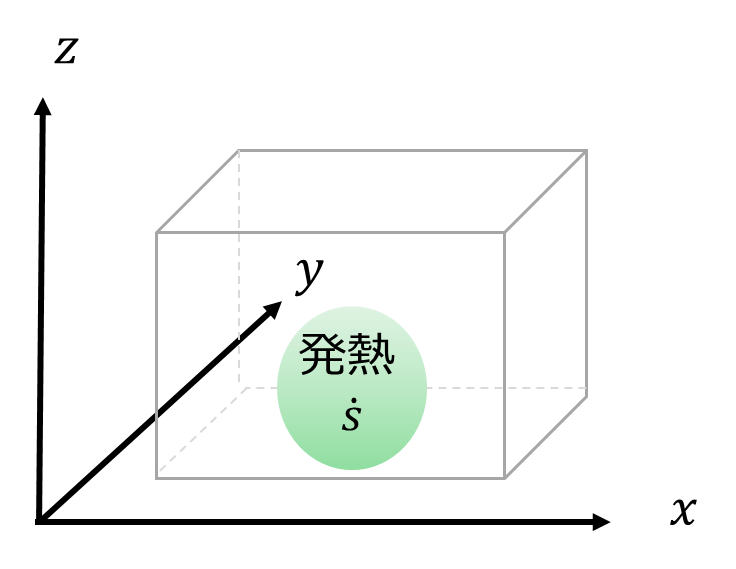
適当にストーブ見ないなものを想像すれば良いでしょう。

これら(6)=(7)+(8)となります。
両辺$\Delta x\Delta y\Delta z$で割ると単位体積当たりの式となります。

\begin{align*}
\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\bigg(k\frac{\partial T}{\partial x}\bigg)+\dot{s}\tag{9}
\end{align*}

これが熱伝導方程式です。

$y,z$方向も考えると、

\begin{align*}
\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\bigg(k\frac{\partial T}{\partial x}\bigg)+\frac{\partial }{\partial x}\bigg(k\frac{\partial T}{\partial x}\bigg)+\frac{\partial }{\partial y}\bigg(k\frac{\partial T}{\partial z}\bigg)+\dot{s}\tag{9}
\end{align*}

熱伝導率$k$は物質によって変わるものです。
加えて温度によっても変わるもので、定数ではなく温度分布がある以上は$k(T(x))=k(x)$のように空間変化するので、微分の外には出すことができません。

ですが、温度変化がそれほど大きくない場合の問題を考える場合は、熱伝導率を一定としても良い近似になります。

\begin{align*}
\rho c\frac{\partial T}{\partial t}=k\bigg(\frac{\partial^2 T}{\partial^2 x}+\frac{\partial^2 T}{\partial^2 y}+\frac{\partial^2 T}{\partial^2 z}\bigg)+\dot{s}\tag{10}
\end{align*}

この形の式を熱伝導方程式と呼ぶこともあります。