こんにちは(@t_kun_kamakiri)
本日は「計算力学技術者試験の熱流体2級」で出てくる内積と外積の解説をします。
内積と外積はベクトル解析などに出てきますが、流体力学のナビエストークス方程式を扱う際には非常によく使うわれます。
理系学部の初学年の解析学で習うですが、社会人になって必ずしも皆が習っているわけではありませんので、これから計算力学技術者の熱流体を勉強する方を対象に問題を通して理解をしていければと思います。
- 計算力学技術者試験の熱流体2級を勉強している方
- ベクトル解析は大学で習ったけど忘れてしまったのでサクッと復習したい方
※微分や偏微分などは理解している方を対象にしています。
では、問題です。
解答はまとめに記載しています。
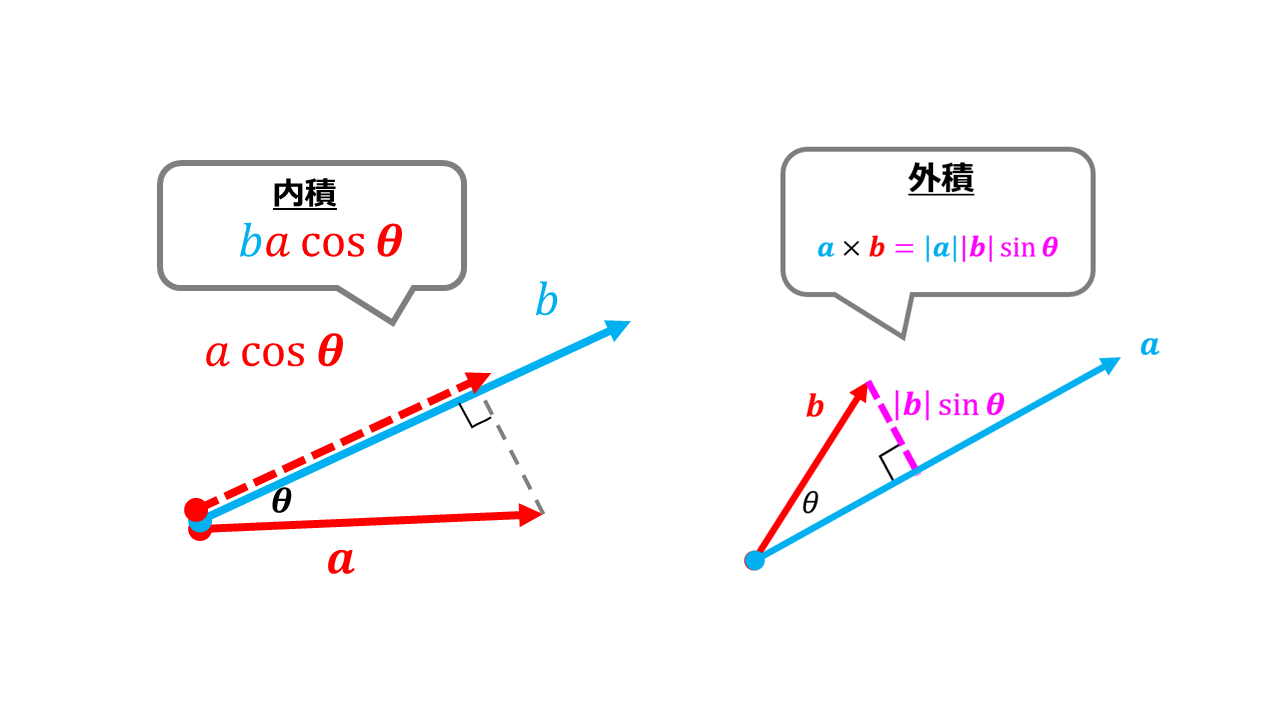
内積とは
内積についてはこちらの記事に詳しく書いておりますのでご確認ください。
高校数学で習うベクトルの表記は文字の頭に「$\rightarrow$(矢印)」を付けて$\vec{u}=(u_{x},u_{y},u_{z})$と表記しますが、大学では多くの場合ベクトル表記は太文字$\boldsymbol{u}=(u_{x},u_{y},u_{z})$で表されます。
ですので、太文字を見るとベクトル(もしくはテンソル)だと思ってください。
内積の計算はどうなるのかというと、任意の2つのベクトルの成分が$\boldsymbol{u}=(u_{x},u_{y},u_{z})$と$\boldsymbol{v}=(v_{x},v_{y},v_{z})$であるとき、
\boldsymbol{u}\cdot \boldsymbol{v}=u_{x}v_{x}+u_{y}v_{y}+u_{z}v_{z}\tag{1}
\end{align*}
となります。
各成分で掛け算を行い、その和を計算することで内積が計算できます。
以下のように「$\cdot$(ドット)」を使わずに横ベクトル$\boldsymbol{u}^\top=\begin{pmatrix}
u_{x}&u_{y}&u_{z}
\end{pmatrix}$と縦ベクトル$\boldsymbol{v}=\begin{pmatrix}
v_{x}\\ v_{y} \\v_{z}
\end{pmatrix}$を使って以下のように書いている場合もあります。
\boldsymbol{u}\cdot \boldsymbol{v}=\boldsymbol{u}^\top \boldsymbol{v}=\begin{pmatrix}
u_{x} &u_{y}&u_{z}
\end{pmatrix}\begin{pmatrix}
v_{x}\\ v_{y} \\v_{z}
\end{pmatrix}=u_{x}v_{x}+u_{y}v_{y}+u_{z}v_{z}\tag{2}
\end{align*}
ベクトルの内積計算の定義を覚えつつ以下のことも合わせて覚えておくことが大事です。
高校の数学でもベクトルの内積計算は出てくるため、内積については抵抗が少ないと思います。ベクトルの内積を忘れている方も、この内積の計算の定義を覚えることがまず第一歩です。
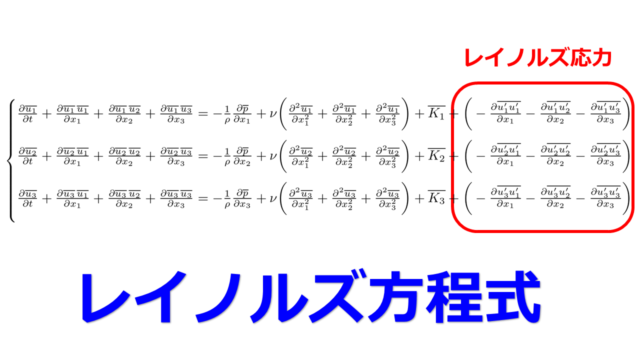
ちなみに内積計算は流体の発散$\nabla\cdot\boldsymbol{u}$の計算でも使われます。
\boldsymbol{\nabla}\cdot\boldsymbol{u}=\frac{\partial u_{x}}{\partial x}+\frac{\partial u_{y}}{\partial y}+\frac{\partial u_{z}}{\partial z}
\end{align*}
ナブラ演算子$\nabla = (\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})$も成分こそ偏微分の演算がありますが、内積の定義は同じ方法が使えるので渦度計算が出てきても慌てることはありません。
外積とは
外積計算は内積計算と違ってちょっと厄介だなと感じている人が多いかと思います。
下記の記事に外積に関する詳しい解説をしていますのでご参考ください。
こちらの記事では、外積計算の方法について4つの方法を紹介しています。
まずはどれかひとつの方法をマスターすることをお勧めします。
僕が外積計算をするときは、「1.べクトルの要素をクロスさせて計算」という方法でほとんど済ませています。
具体的な計算をするときは3次元計算までなので1番の方法だけ覚えておけばよいかと思いますが、もっとスマートに記述したい場合や変数が多くなった場合には「3.エディントンンのイプシロン$\varepsilon_{ijk}$を使う」という方法が良いです。
が・・・・慣れないと扱いづらいです。材料力学や流体力学、相対性理論などではしばしば出てくるので今のうちに慣れておくのもよいでしょうね。
本記事では「ベクトルの要素をクロスさせて計算」のみ紹介します。
2つのベクトルの成分をクロスしてもうひとつの成分に書くという方法です。
絵を使って説明した方がわかりやすいので↓こちらを見てください。
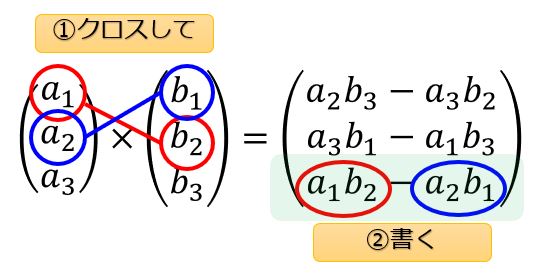
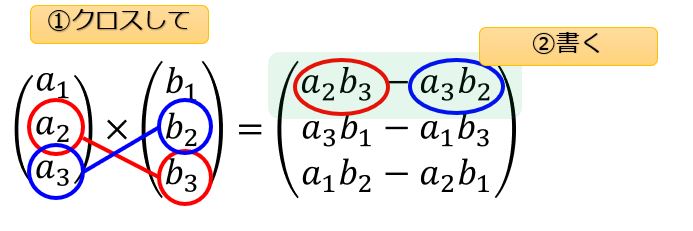
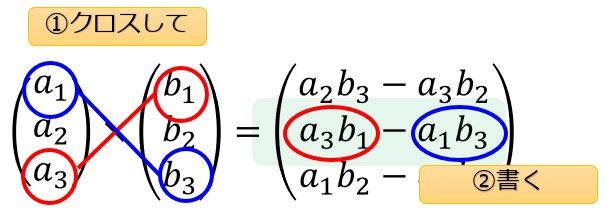
まとめると、
\boldsymbol{a}\times\boldsymbol{b}=\begin{pmatrix}
a_{2}b_{3}-a_{3}b_{2}\\\
a_{3}b_{1}-a_{1}b_{3}\\\
a_{1}b_{2}-a_{2}b_{1}
\end{pmatrix}
\end{align*}
となります。
任意の2つのベクトルの成分が$\boldsymbol{u}=(u_{x},u_{y},u_{z})$と$(\boldsymbol{v}=(v_{x},v_{y},v_{z})$であるとき、
\boldsymbol{u}\times\boldsymbol{v}=\begin{pmatrix}
u_{y}v_{z}-u_{z}v_{y}\\\
u_{z}v_{x}-u_{x}v_{z}\\\
u_{x}v_{y}-u_{y}v_{x}
\end{pmatrix}\tag{3}
\end{align*}
となります。
内積と違うところは色々ありますが、以下のような簡単な計算結果ですら違いますので要注意です。
ちなみに、外積は渦度$\boldsymbol{\omega}=\boldsymbol{\nabla}\times\boldsymbol{v}$の計算をする際に出てきます。
\boldsymbol{\nabla}\times\boldsymbol{u}&=
\begin{pmatrix}
\frac{\partial}{\partial x}\\
\frac{\partial}{\partial y}\\
\frac{\partial}{\partial z}
\end{pmatrix}\times
\begin{pmatrix}
u_{x}\\
u_{y}\\
u_{z}\\
\end{pmatrix}\\
&=\begin{pmatrix}
\frac{\partial u_{z}}{\partial y}-\frac{\partial u_{y}}{\partial z}\\
\frac{\partial u_{x}}{\partial z}-\frac{\partial u_{z}}{\partial x}\\
\frac{\partial u_{y}}{\partial x}-\frac{\partial u_{x}}{\partial y}
\end{pmatrix}
\end{align*}
ナブラ演算子$\nabla = (\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})$も成分こそ偏微分の演算がありますが、外積の定義は同じ方法が使えるので渦度計算が出てきても慌てることはありません。
まとめ
計算の結果はノートにまとめます。
再度、内積と外積の計算方法を押えておきましょう。
内積の計算
\boldsymbol{u}\cdot \boldsymbol{v}=\boldsymbol{u}^\top \boldsymbol{v}=\begin{pmatrix}
u_{x} &u_{y}&u_{z}
\end{pmatrix}\begin{pmatrix}
v_{x}\\ v_{y} \\v_{z}
\end{pmatrix}=u_{x}v_{x}+u_{y}v_{y}+u_{z}v_{z}\tag{2}
\end{align*}
外積の計算
\boldsymbol{u}\times\boldsymbol{v}=\begin{pmatrix}
u_{y}v_{z}-u_{z}v_{y}\\\
u_{z}v_{x}-u_{x}v_{z}\\\
u_{x}v_{y}-u_{y}v_{x}
\end{pmatrix}\tag{3}
\end{align*}
計算力学技術者のための問題アプリ
計算力学技術者熱流体2級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
お勧めの参考書
ベクトル解析は以下の参考書で学ぶのがお勧めです。