【粒子追跡ソルバで粒子径を正規分布に！】OpenFOAMのMPPICFoam粒子追跡の設定

前回の記事ではOpenFOAMの粒子追跡の設定について解説しました。

チュートリアルの確認

今回はMPPICFoamを例に粒子径分布の設定を確認します。

粒子間相互作用をマクロで近似するMPPIC法。
・packing model
・collisional damping models
・collisional isotropy model
・blended acceleration model
これらがOpenFOAMに実装されていると。https://t.co/3Q7GgWQiM4

— カマキリ🐲計算力学頑張る (@t_kun_kamakiri) July 14, 2023

MPPICFoamは粒子間相互作用をマクロで近似する手法で通常の粒子間衝突の計算よりは高速です。
チュートリアルを作業フォルダにコピーします。

cp -r /usr/lib/openfoam/openfoam2412/tutorials/lagrangian/MPPICFoam/Goldschmidt .

1	cp -r /usr/lib/openfoam/openfoam2412/tutorials/lagrangian/MPPICFoam/Goldschmidt .

$FOAM_TUTORIALS = /usr/lib/openfoam/openfoam2412

OpenFOAMの粒子追跡はMPPICFoam以外にも以下のソルバがあります。

ソルバ名	主な用途・特徴
`DPMFoam`	単相流体中の粒子の運動を解く（Discrete Phase Model）
`MPPICFoam`	多数粒子の相互作用を扱う連続体近似粒子法（MP-PIC 法）
`MPPICDyMFoam`	MPPICFoamに移動メッシュ（Dynamic Mesh）を加えたバージョン
`coalChemistryFoam`	石炭燃焼と粒子の化学反応を扱うソルバ
`icoUncoupledKinematicParcelFoam`	非圧縮流体中の運動粒子（運動の影響を流体に与えない）の解法
`icoUncoupledKinematicParcelDyMFoam`	上記に動的メッシュ（DyM）機能を追加
`kinematicParcelFoam`	運動粒子と流体との双方向連成を含むモデル
`uncoupledKinematicParcelDyMFoam`	粒子運動は流体に影響を与えない＋動的メッシュ
`reactingParcelFoam`	粒子が化学反応・蒸発するモデル（例えば液滴燃焼）
`reactingHeterogenousParcelFoam`	表面反応などの異種反応を含む粒子の化学反応モデル
`simpleReactingParcelFoam`	簡易モデルによる粒子反応（例えば簡略化した燃焼モデル）
`sprayFoam`	スプレー（粒子の噴霧）と蒸発・反応などを考慮した燃焼モデル

粒子に関係するファイルを確認します。

まずは粒子の初期配置の設定を確認します。

constant/kinematicCloudPositions

FoamFile
{
    version     2.0;
    format      ascii;
    class       vectorField;
    object      kinematicCloudPositions;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

(
(-0.0060 -0.0735 0.0015)
(-0.0030 -0.0735 0.0015)
(0.0000 -0.0735 0.0015)
(0.0030 -0.0735 0.0015)
...（省略)...
)

FoamFile

{

version 2.0;

format ascii;

class vectorField;

object kinematicCloudPositions;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

(

(-0.0060 -0.0735 0.0015)

(-0.0030 -0.0735 0.0015)

(0.0000 -0.0735 0.0015)

(0.0030 -0.0735 0.0015)

...（省略)...

)

上記の設定を以下のファイルで設定します。

constant/kinematicCloudProperties

...（省略)...
subModels
{
    particleForces
    {
        PlessisMasliyahDrag
        {
            alphac alpha.air;
        }
        gravity;
    }

    injectionModels
    {
        model1
        {
            type            manualInjection;
            massTotal       0;
            parcelBasisType fixed;
            nParticle       1;
            SOI             0;
            positionsFile   "kinematicCloudPositions";
            U0              (0 0 0);
            sizeDistribution
            {
                type        fixedValue;
                fixedValueDistribution
                {
                    value   0.0025;
                }
            }
        }
    }
...（省略)...

...（省略)...

subModels

{

particleForces

{

PlessisMasliyahDrag

{

alphac alpha.air;

}

gravity;

}

injectionModels

{

model1

{

type manualInjection;

massTotal 0;

parcelBasisType fixed;

nParticle 1;

SOI 0;

positionsFile "kinematicCloudPositions";

U0 (0 0 0);

sizeDistribution

{

type fixedValue;

fixedValueDistribution

{

value 0.0025;

}

...（省略)...

粒子径分布はsizeDistributionのtype fixedValue;の部分で設定しています。
チュートリアルのデフォルトでは一定値0.0025[m]の粒子径が設定されています。

ちなみにpositionsFile "kinematicCloudPositions"; で先ほどの粒子の初期配置の設定ファイルを指定しています。

チュートリアルの計算を実行し、粒子径分布を確認してみましょう。

blockMesh # メッシュ作成
MPPICFoam # 計算実行

1 2	blockMesh # メッシュ作成 MPPICFoam # 計算実行

計算結果は以下のようになります。

ちなみに粒子径の分布各時刻で出力されており、例えば0.01/lagrangian/kinematicCloud/dを確認すると以下のように書かれています。

24750{0.0025}

1	24750{0.0025}

これは全ての粒子直径が0.0025 [m]となっているという意味です。

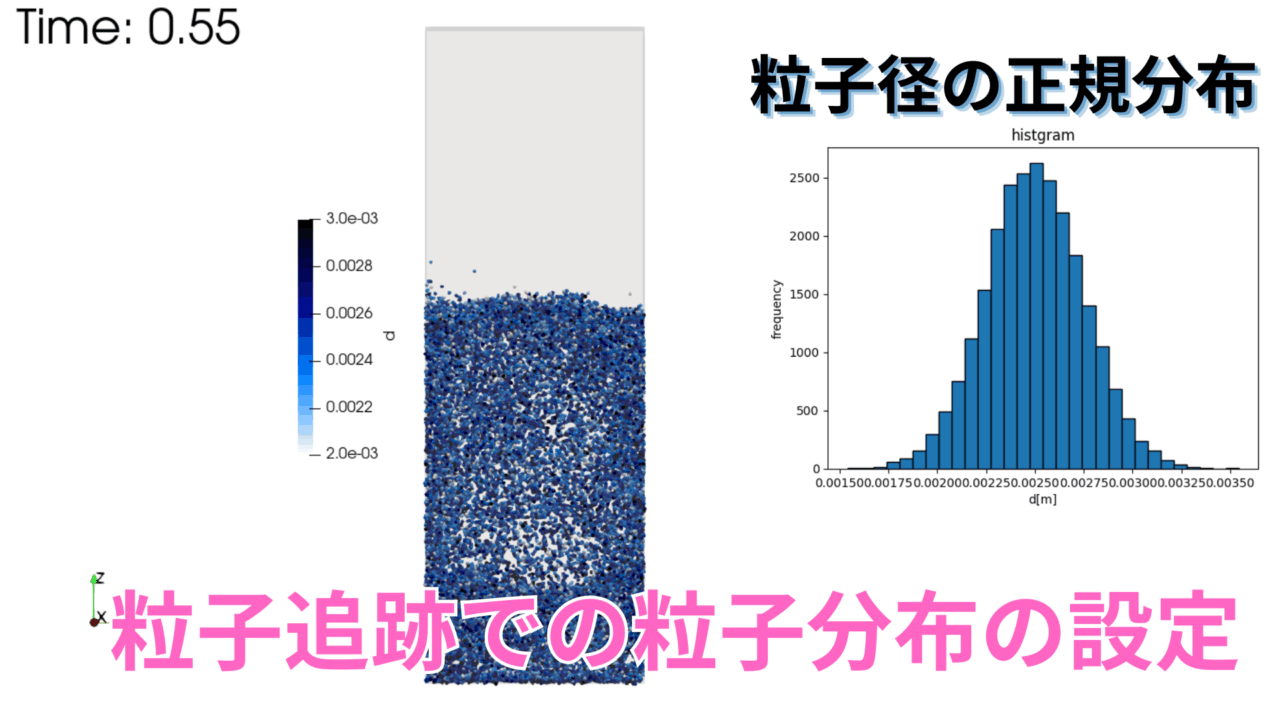
粒子径がすべての粒子で同じなので、粒子径のコンタの色は同じ色になっています。

いろいろな粒子直径分布

粒子直径の設定はこちらに書かれております。

クラス名	分布の種類	数式（PDFなど）	説明
`binned`	離散分布	—（個別のサイズと確率ペア）	(サイズ, 確率)の離散データからサンプリング
`exponential`	両側切断指数分布	$f(x) = \frac{\lambda e^{-\lambda x}}{e^{-\lambda x_{\min}} – e^{-\lambda x_{\max}}} \quad (x_{\min} \le x \le x_{\max})$	切断付きの指数分布
`fixedValue`	定値	—	単一サイズの粒子
`general`	任意分布（PDF/CDF）	—	任意の関数形で与えた分布 (補間で定義)
`massRosinRammler`	質量補正Rosin-Rammler	$f(x) = \frac{n}{x} \left( \frac{x}{x_0} \right)^n \exp\left( -\left( \frac{x}{x_0} \right)^n \right) $（補正あり）	固定質量パーセルに対応した補正付き分布
`multiNormal`	正規分布の混合	$f(x) = \sum_{i=1}^k w_i \cdot \frac{1}{\sqrt{2\pi \sigma_i^2}} \exp\left(-\frac{(x – \mu_i)^2}{2\sigma_i^2} \right)$	複数の正規分布の加重和
`normal`	両側切断正規分布	※ $$z = \frac{x – \mu}{\sigma}$$	切断正規分布、正規化あり
`RosinRammler`	両側切断Rosin-Rammler	$\frac{n}{x} \left( \frac{x}{x_0} \right)^n \exp\left( -\left( \frac{x}{x_0} \right)^n \right) \quad (x_{\min} \le x \le x_{\max}) $$	粒子サイズ分布で一般的な関数
`uniform`	両側切断一様分布	$f(x) = \frac{1}{x_{\max} – x_{\min}} \quad (x_{\min} \le x \le x_{\max})$	等確率の単純な分布

粒子径分布が正規分布に従う場合

平均値：$\mu=0.00025$
標準偏差：$\sigma=0.00025$
最大・最小：0.001、0.005

\begin{align*}
f(x) = \frac{1}{\sigma \sqrt{2\pi}} \cdot \frac{\exp\left(-\frac{(x – \mu)^2}{2\sigma^2} \right)}{\Phi(z_{\max}) – \Phi(z_{\min})} \quad (x_{\min} \le x \le x_{\max})
\end{align*}

constant/kinematicCloudProperties

subModels
{
    particleForces
    {
        PlessisMasliyahDrag
        {
            alphac alpha.air;
        }
        gravity;
    }

    injectionModels
    {
        model1
        {
            type            manualInjection;
            massTotal       0;
            parcelBasisType fixed;
            nParticle       1;
            SOI             0;
            positionsFile   "kinematicCloudPositions";
            U0              (0 0 0);
            sizeDistribution
            {
                // type        fixedValue;
                // fixedValueDistribution
                // {
                //     value   0.0025;
                // }
                type        normal;
                normalDistribution
                {
                    expectation        0.0025; //mu
                    variance     0.00025; //sigma
                    minValue  0.001;
                    maxValue  0.005;
                }
            }
        }
    }

subModels

{

particleForces

{

PlessisMasliyahDrag

{

alphac alpha.air;

}

gravity;

}

injectionModels

{

model1

{

type manualInjection;

massTotal 0;

parcelBasisType fixed;

nParticle 1;

SOI 0;

positionsFile "kinematicCloudPositions";

U0 (0 0 0);

sizeDistribution

{

// type fixedValue;

// fixedValueDistribution

// {

// value 0.0025;

// }

type normal;

normalDistribution

{

expectation 0.0025; //mu

variance 0.00025; //sigma

minValue 0.001;

maxValue 0.005;

}

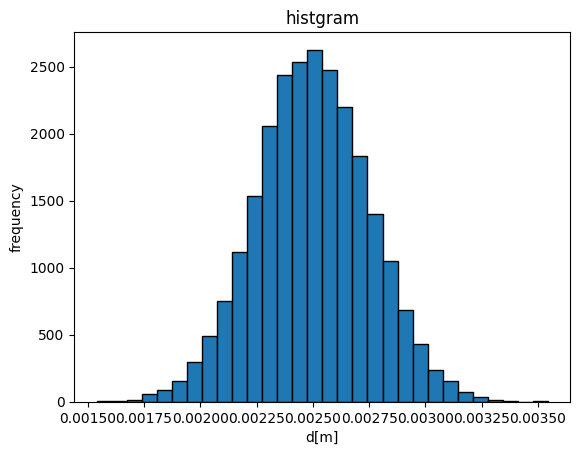
再度計算すると粒子径分布のコンタの色が変わります。

粒子径の分布各時刻で出力されており、例えば0.01/lagrangian/kinematicCloud/dを確認すると以下のように書かれています。

24750
(
0.00266857
0.00278219
0.00269801
...(省略)...
)

24750

(

0.00266857

0.00278219

0.00269801

...(省略)...

)

こちらをPythonスクリプトでヒストグラムにしますと以下のような正規分布に近い形になります。

うまく粒子径分布の設定ができていますね。

参考までにヒストグラムにした際に使用したプログラムを書いておきます。

import numpy as np
import matplotlib.pyplot as plt

# ファイルパスを定義
file_path = '0.01/lagrangian/kinematicCloud/d'

# ファイルを読み込む
with open(file_path, 'r') as file:
    lines = file.readlines()

# スカラー値の開始位置を特定（ヘッダー部分をスキップ）
start_index = lines.index('(\n') + 1

# スカラー値を抽出
scalar_values = []
for line in lines[start_index:]:
    stripped_line = line.strip()
    # 行が空でなく、終了を示す括弧でなく、数値に変換可能な場合、値を追加
    try:
        scalar_values.append(float(stripped_line))
    except ValueError:
        # 数値に変換できない場合はスキップ
        continue

# NumPy配列に変換
scalar_values = np.array(scalar_values)
# ヒストグラムを作成
plt.hist(scalar_values, bins=30, edgecolor='black')
plt.title('histgram')
plt.xlabel('d[m]')
plt.ylabel('frequency')

# プロットを表示
plt.show()