本日は、ルジャンドル変換を勉強したのでまとめてみました(^^)/
このルジャンドル変換は数学的にもっと奥が深いような気がしますが、現時点の自分が理解した範囲で記述しようと思います。
まずはルジャンドル変換の意味と、その応用例を示しましょう。
ルジャンドル変換を絵でイメージ
ルジャンドル変換(数学者:アドリアン=マリ・ルジャンドル)
凸解析において、関数の変数を変えるために用いられる変換『下に凸な関数 f(x) は (x, f(x)) の点の集合によって表現できるが、
”傾き”と”y切片”の値で指定される接線の集合によっても表現できる』ということに基いています。
「関数の変数を変える」というのを式で書くと、
\(g(p)=min(px-f(x))\)
※\(p=\frac{df(x)}{dx}\)ルジャンドル変換は\(f(x)\)から別の関数\(g(p)\)を作り出す手続き。
言葉で言われてもよくわかりません(笑)
上述の表現を絵で書いてみます。
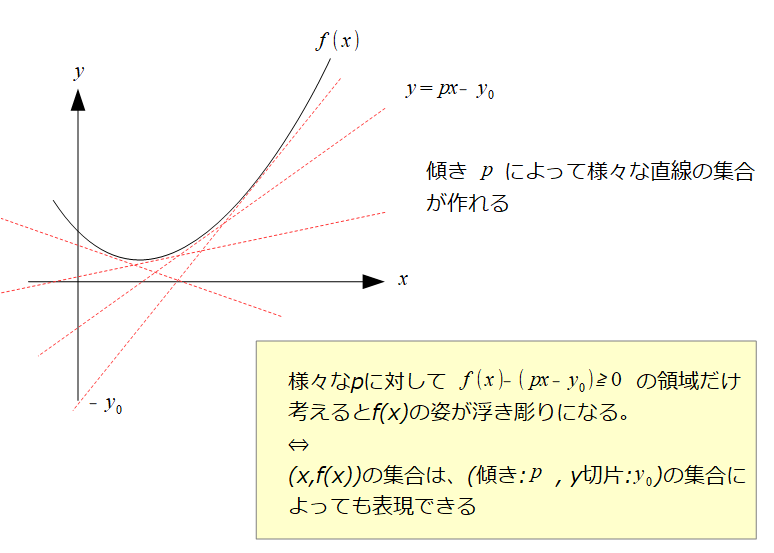
様々な\(p\)と書いていますが、\(x\)を動かして\(f(x)\)の接線になるように\(p\)を選ぶことにします。
ここで、y切片の\(y_{0}\)は傾き\(p\)の値によって変化するので、\(p\)の関数と見て\(y_{0}=g(p)\)と置きます。
すると、\((x,f(x))\)の集合を\(y=px-g(p)\)で表現できそうです。
\((x,f(x))\)の集合について特に、
- 『様々な\(p\)により、\(f(x))\)の接線となる\(p\)とは\(min(f(x)-(px-g(p))=0\)と表現できます』
↓そうなるような - 『\((x,p)\)の組み合わせ』
なら\((x,f(x))\)の集合を表現できていますね。
ひとつひとつ絵で書いてみましょう。
『様々な\(p\)により、\(f(x))\)の接線となる\(p\)とは\(min(f(x)-(px-g(p))=0\)と表現できます』
これを絵で書きます。
単に\(y=px-y_{0}\)ならこのように適当に、接線と言わず直線を引けます。
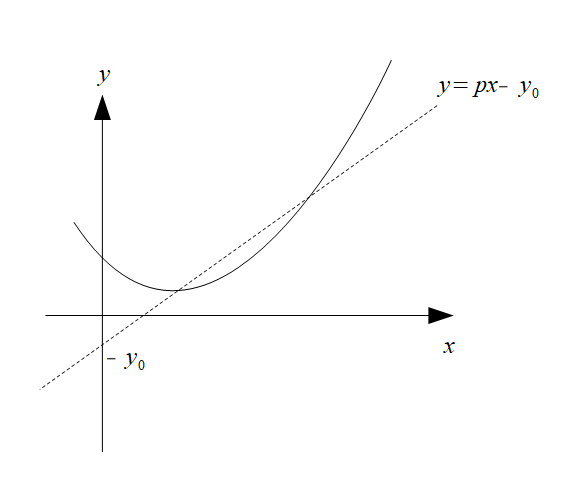
色々\(x\)を動かしていったときに、\(f(x)\)とこの直線の\(y\)座標との差が最小になるように\(p\)を決めます。
それが式で表現すると、\(min(f(x)-(px-g(p))=0\)となります。
それを絵で表現すると下記のように青の距離\(f(x)-(px-y_{0})\)などではなく、赤丸●の部分(距離が0、すなわち接線にしたとき)を示しています。
この時直線は赤色のように\(f(x)\)の接線になっています。

これによって決められた\(y_{0}\)が\(y_{0}=g(p)\)となります。
\(min(f(x)-(px-g(p))=0\)は、\(g(p)=min((px-f(x)\)と見ることもできます。
すなわち、ルジャンドル変換は\(f(x)\)から別の関数\(g(p)\)を作り出す手続きであると見れます。
『\((x,p)\)の組み合わせなら\((x,f(x))\)の集合』
これを絵で書くと、赤丸●の部分だけの集合で\((x,f(x))\)が表現できていることがわかります。
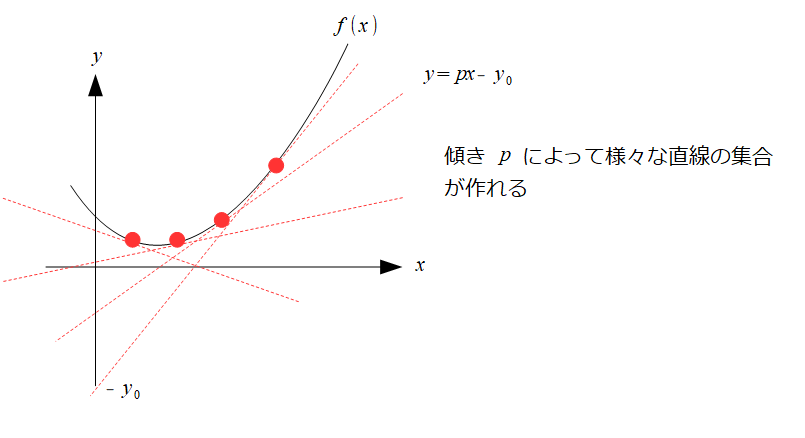
ルジャンドル変換
\(g(p)=min(px-f(x))\)
※\(p=\frac{df(x)}{dx}\)ルジャンドル変換は\(f(x)\)から別の関数\(g(p)\)を作り出す手続き。
これは特に\((x,f(x))\)を、変数\(p\)として\((p,g(p))\)と見ることができる(と解釈しています(笑))。
※\(p=\frac{df(x)}{dx}\)や\(y_{0}\)の符号はどちらでも良いような気がします(自信なし・・・)。
絵では\(p\)も\(y_{0}\)も正の値っぽく書きましたが、別に絵の書き方によっては負の値に見えててもいいわけですよね。
ルジャンドル変換の利用例
ルジャンドル変換は、数学的な手続きのみならず物理でもよく出没します。
というわけで、いくつか例を挙げてみたいと思います(^^)/
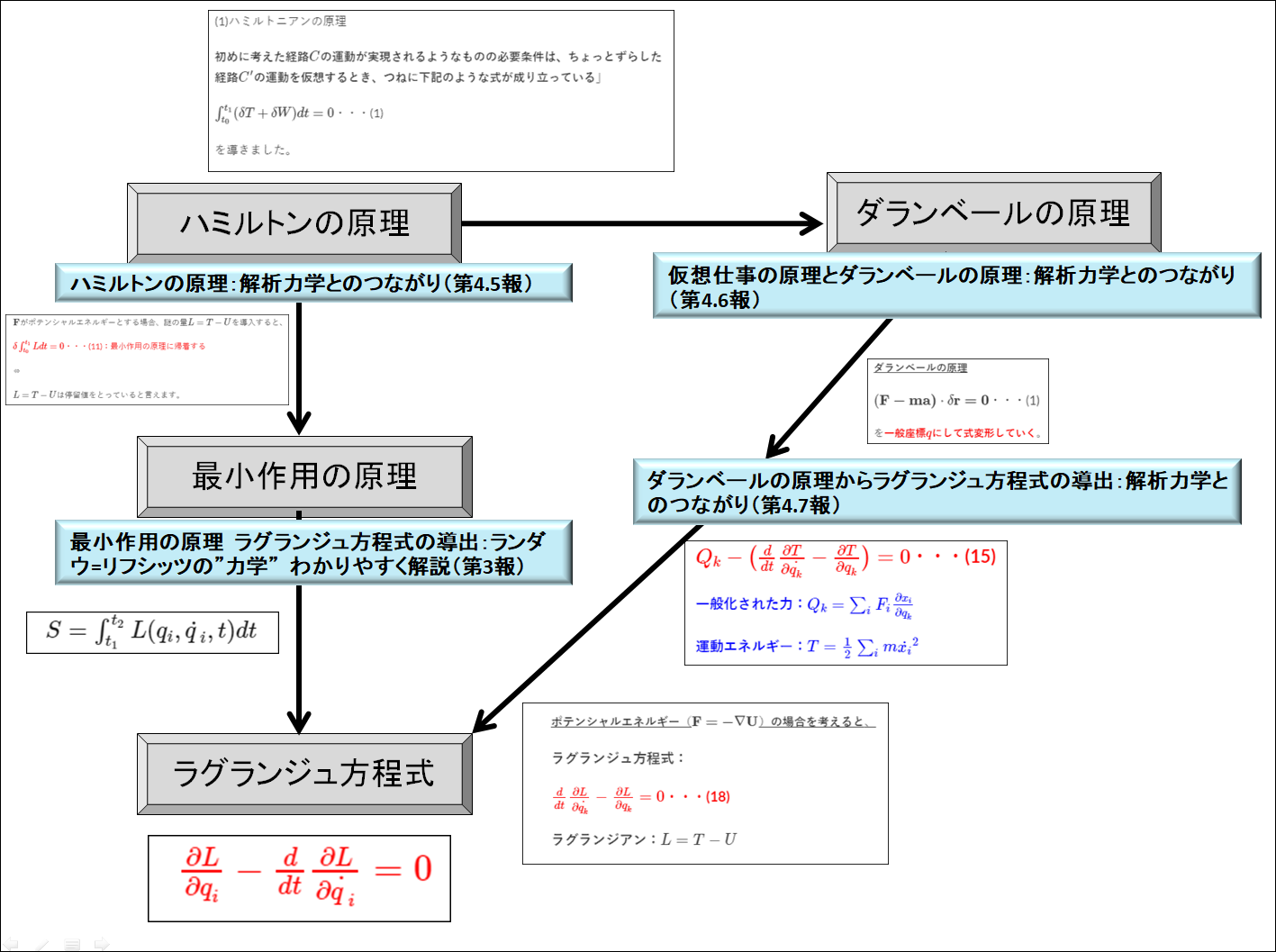
解析力学
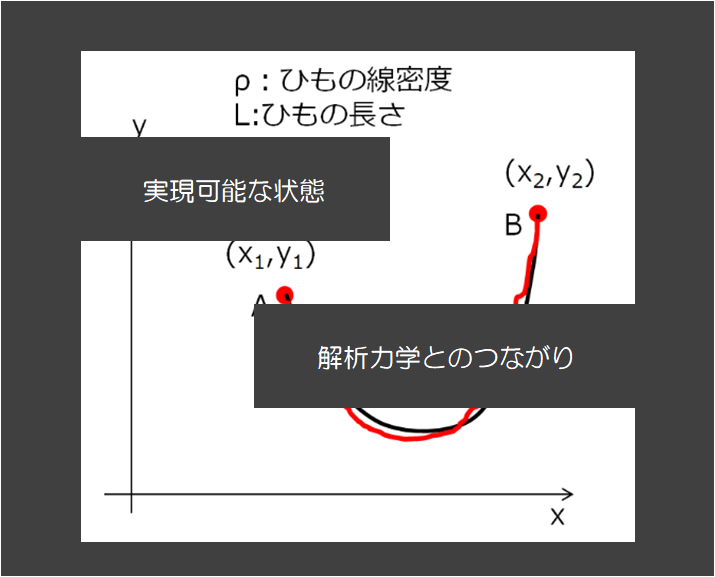
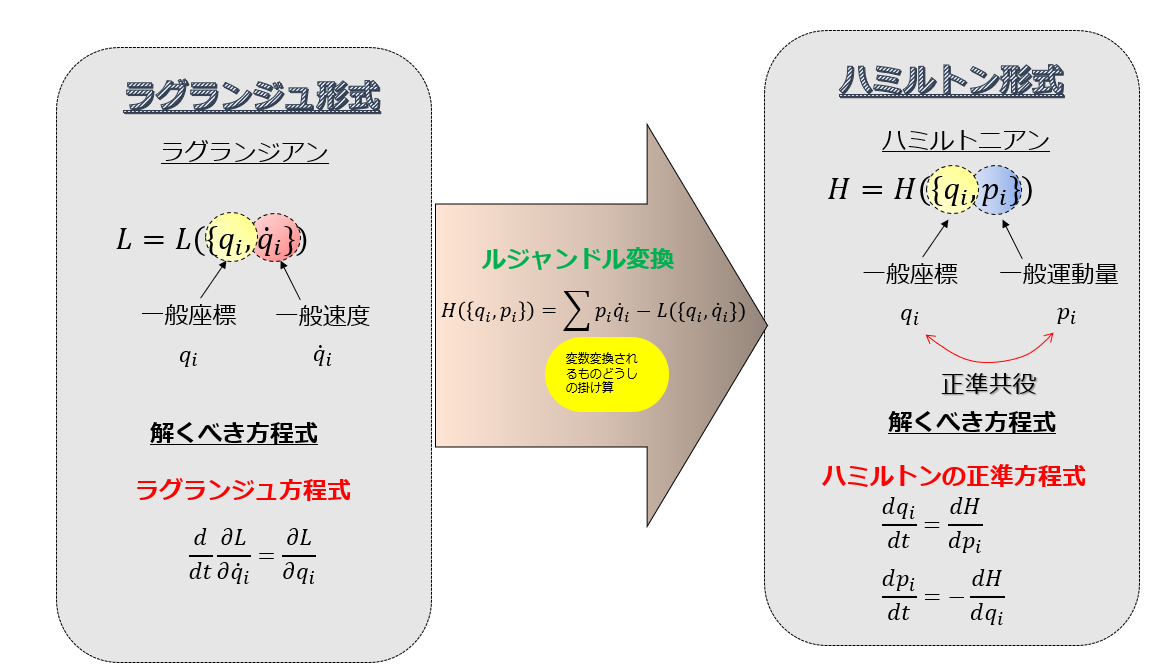
系の力学的状態は、一般座標と一般速度\((q,\dot{q})\)で記述することが唯一の方法ではなく、一般座標と一般運動量\((q,p)\)で表現することの方が良い場合が多い。
すなわち、ラグランジアン\(L(q,\dot{q})\)からハミルトニアン\(H(q,p)\)に変換するときにルジャンドル変換を使います。
ラグランジアンからハミルトニアンへ
運動量は\(p=\frac{\partial L} {\partial \dot{q}}\)でしたね。
熱力学
以下の熱力学的関数を変換する際にルジャンドル変換が使われます。
内部エネルギー:\(U(S, V, N)\)
エンタルピー :\(H(S, p, N)\)
ヘルムホルツの自由エネルギー :\(F(T, V, N)\):
ギブスの自由エネルギー\(G(T, p, N)\)
\(V\):体積
\(P\):圧力
\(S\):エントロピー
\(T\):温度
内部エネルギーからエンタルピー
\(U(S,V)=H(S,P)-PV\)
or
\(H(S,P)=U(S,V)+PV\)
等圧条件下にある系で、吸熱すると内部のエネルギーと外部にする仕事を考えた熱力学の関数がエンタルピー\(H\)です。
内部エネルギーからヘルムホルトの自由エネルギーへ
\(F(T,V)=U(S,V)-TS\)
化学変化を含めた熱力学的系の等温過程において、系の最大仕事(潜在的な仕事能力)、自発的変化の方向、平衡条件などを表す指標となります。
温度が決定している状態で、系の平衡状態を決めるのは、内部エネルギー\(U\)が最小だけでは情報が足らず、エントロピー\(S\)(乱雑さ)も考慮して系の状態が決定される熱力学の関数がヘルムホルツの自由エネルギー\(F\)です。
例えば、温度が高い場合は式を見てお分かりのように、\(TS\)があるのでエントロピー\(S\)を大きくした方がヘルムホルツの自由エネルギー\(F\)は最小の方向に向かいますね。
だから、高温化では状態はランダム(激しく運動する)な方向に系が状態を取りたがるというような理解の仕方ができます。
ヘルムホルトの自由エネルギーからギブスの自由エネルギーへ
\(G(T,P)=F(T,V)+PV\)
等温等圧過程(容積が変化を考慮)の自由エネルギーを考えたい場合に威力を発揮する熱力学の関数がギブスの自由エネルギー\(G\)です。
まとめ
ルジャンドル変換
\(g(p)=min(px-f(x))\)
※\(p=\frac{df(x)}{dx}\)ルジャンドル変換は\(f(x)\)から別の関数\(g(p)\)を作り出す手続き。
これを使って、解析力学や熱力学でよく見かける関数の変換の例を挙げてみました(^^)/
次回
ルジャンドル変換をまた考えるのですが、もう少し対称性が見える形の議論ができると嬉しいかなと考えています。
解析力学のハミルトンの正準方程式ですね。
そういえば、熱力学でも似たような関係式がありましたね。
いつか勉強のために記事にまとめたいですね(^^)
完全な余談
\(\dot{q}\)を書くとき、texでは「\dot{q}」とこのように書くのですよね。
さっさと変数を\(p\)に変えてくれたら、texでものすごく書きやすくなります(笑)






















分かりやすくて直感的な理解を有り難うございます。
コメントありがとうございます。
ブログはじめたて当初の勉強ログの内容でしたので、間違いあるかもしれません。
その際はご連絡いただけますと幸いです。