どうも(^^)/
点変換を解析力学で勉強した母関数を用いて表現したいと思います。
本記事は、「ランダウ=リフシッツの”力学”」のP.183の注釈についての内容です。

点変換による説明は↓こちらの記事にまとめました。
結論から言います。
点変換による母関数の表記は、下記のように、
\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}f_{i}(\{q\},t)P_{i}\end{align*}
と書けます。
はい、以上です・・・・・
と言ってしまえばそれまでですが、少し中身を見ていきましょう(^^)/
点変換とは
点変換とは何でしょうか。これも前回の記事に書きましたが少々復習します。
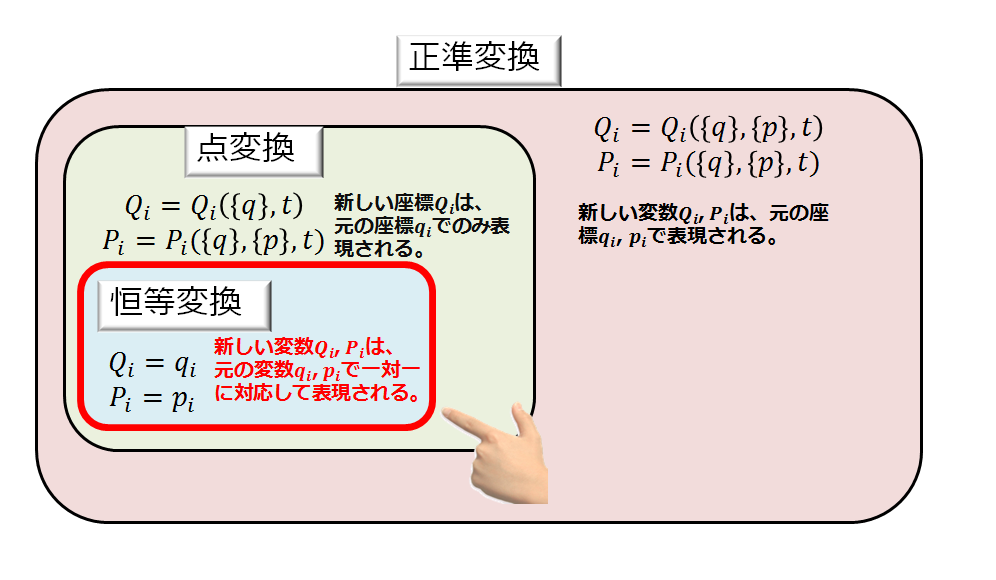
一般座標\({q}\)(自由度\(f\))に対して、別の座標\({Q}\)(自由度\(f\))に変換するとき、
・・・
と、座標変換に対して元の座標と新しい別の座標が一対一に対応している変換のことを点変換と言います。
その逆も言えます。
座標変換に対して元の座標と新しい別の座標が一対一に対応しているので、下記のようにも書けます。
・・・
これは何も珍しい話ではないです。
座標の表し方はデカルト座標(\(x,y,z\))のみではなかったはずです。
例えば、極座標表示で下記のようにすることもできます。

このとき、
と書けます。
これを変数がわかるように書くと、
これは逆に、(1)(2)(3)式を式変形すると、
とできます。
もっと一般的に書いたらどうなるのかと言いますと、
と書けるのです。
これは元の座標の変数を使って、新しい座標の変数を作ったことになります。
時間を陽に含んでいるとしても良いので、
とできます。
母関数のまとめ
上記のように点変換が何かを見ましたが、それを母関数で表現したいと思います。
その前に、母関数を求めてどういう手順で、問題を取り扱うのかの手順を書いておきましょう。
母関数は、元の変数\({q}\)と\(p\)から、別の新しい変数\(Q\)と\(P\)に変換したときに、ハミルトンの正準方程式の形を保ったまま変換するための橋渡しになる関数になります。
※ハミルトンの正準方程式の形を保ちつつ、元の変数\(\{q\}\)と\(\{p\}\)から一組選び、新しい変数\(\{Q\}\)と\(\{P\}\)に変換する変換のことを正準変換と言います。
そこで、母関数は変数として元の変数\(\{q\}\)と\(\{p\}\)から一組選び、新しい変数\(\{Q\}\)と\(\{P\}\)から一組選ぶ方法の合計4パターンの変数の選び方があるのです。
それを一覧にまとめると下記のようになります。
母関数 |
母関数の変換 |
元の変数 |
新しい変数 |
ハミルトニアン | ||
| \(q_{i}\) | \(p_{i}\) | \(Q_{i}\) | \(P_{i}\) | \({H}’\) | ||
|
\(W_{1}\) 変数 \(\{q\}\), \(\{Q\}\) |
\(W_{1}\) | \(\frac{\partial W_{1}}{\partial q_{i}}\) | \(-\frac{\partial W_{1}}{\partial Q_{i}}\) | \(H+\frac{\partial W_{1}}{\partial t}\) | ||
|
\(W_{2}\) 変数 \(\{q\}\), \(\{P\}\) |
\(W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\) \(W_{2}=W_{1}+\sum_{i}P_{i}Q_{i}\) |
\(\frac{\partial W_{2}}{\partial q_{i}}\) | \(\frac{\partial W_{2}}{\partial P_{i}}\) | \(H+\frac{\partial W_{2}}{\partial t}\) | ||
|
\(W_{3}\) 変数 \(\{p\}\), \(\{P\}\) |
\(W_{3}=W_{2}-\sum_{i}p_{i}q_{i}\) \(W_{3}=W_{1}+\sum_{i}P_{i}Q_{i}-\sum_{i}p_{i}q_{i}\) |
\(-\frac{\partial W_{3}}{\partial p_{i}}\) | \(\frac{\partial W_{3}}{\partial P_{i}}\) | \(H+\frac{\partial W_{3}}{\partial t}\) | ||
|
\(W_{4}\) 変数 \(\{p\}\), \(\{Q\}\) |
\(W_{4}=W_{3}-\sum_{i}P_{i}Q_{i}\) \(W_{4}=W_{1}-\sum_{i}p_{i}q_{i}\) |
\(-\frac{\partial W_{4}}{\partial p_{i}}\) | \(-\frac{\partial W_{4}}{\partial Q_{i}}\) | \(H+\frac{\partial W_{4}}{\partial t}\) | ||
※正準変換後のハミルトニアン\({H}’\)は変数をどれを使っても(母関数をどれを使っても)変わりません。
詳しくはこちらの記事をお読みください。
証明は省きますが、これは数学的にはルジャンドル変換を施せば簡単に変換できます(地味ですが、一度やってみると良いでしょう)
そして仮に、変数として\(q\)と\(Q\)を選んだとして、問題を取り扱う際の手順は下記の流れになります。
(1)\(W_{1}(\{q\},\{Q\},t)\)が与えらると、
↓
(2)元の変数「\(\{q\}\),\(\{p\}\)」と
新しい変数「\(\{Q\}\)と\(\{P\}\)」との関係を与え、
※上の表から母関数を与えれば、「\(\{q\}\),\(\{p\}\)」や「\(\{Q\}\)と\(\{P\}\)」の関係式を知ることができる。↓
(3)新しいハミルトニアン\({H}’\)を与える
↓
(4)さらに、ハミルトニアン\({H}’\)から⑪⑫式によって、運動方程式を与える
↓
(5)その運動方程式を解けば、新しい変数「\(\{Q\}\)と\(\{P\}\)」の時刻変化がわかる
このようにして、母関数を与えられると問題が解けるということになります。
それでは、点変換に対して、母関数を用いて表現してみましょう。
点変換を母関数で表現してみる
点変換による母関数の表現は、
です。
※変数は\(\{q\},\{P\}\)なので、上の表と同じ表記で母関数を\(W_{2}\)としておきます。
つぎに、上の手順の(2)で、
により、\(Q_{i}\)と\(p_{i}\)が求まります。
では、計算を進めてみましょう。
(7)式は簡単にできます
(7)式より、
※和の添え字は\(j\)としておきました。
※\(i\)以外の微分はすべて0となり、消えます。
このようにして、(1)(2)(3)のような形の、新しい座標\(Q_{i}\)は元の座標\(q_{i}\)だけで表現することができました。
このように表記できる変換のことを点変換と言います。
つまり、点変換の母関数は、
\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}f_{i}(\{q\},t)P_{i}\end{align*}
と表現できることが示せました。
一応、\(P_{i}\)についてもやっておきましょう。
(8)式を計算する
※和の添え字は\(j\)に変えておきます。
(9)式より、
であるので、(10)式は、
結局、\(Q_{j}\)に対する偏微分しかかからないので、
となりました。
まとめ
点変換の意味
一般座標\({q}\)(自由度\(f\))に対して、別の座標\({Q}\)(自由度\(f\))に変換するとき、\begin{align*}Q_{1}=Q_{1}(\{q\},t)\end{align*}\begin{align*}Q_{2}=Q_{2}(\{q\},t)\end{align*}・・・
\begin{align*}Q_{f}=Q_{f}(\{q\},t)\end{align*}と、座標変換に対して元の座標と新しい別の座標が一対一に対応している変換のことを点変換と言います。
点変換に対する母関数の表現
\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}f_{i}(\{q\},t)P_{i}\end{align*}
点変換による母関数W_{2}による\(Q_{i}\)と\(p_{i}\)の関係式
\begin{align*}Q_{i}=f_{i}(\{q\},t)\cdot\cdot\cdot (9)\end{align*}
\begin{align*}p_{i}=\sum_{j}\frac{\partial Q_{j}}{\partial q_{i}}P_{j}\cdot\cdot\cdot (12)\end{align*}
補足
\begin{align*}Q_{i}=f_{i}(\{q\},t)\cdot\cdot\cdot (9)\end{align*}
\begin{align*}p_{i}=\sum_{j}\frac{\partial Q_{j}}{\partial q_{i}}P_{j}\cdot\cdot\cdot (12)\end{align*}
と一応、点変換による母関数W_{2}による\(Q_{i}\)と\(p_{i}\)の関係式は得ることができたのですが、できれば新しい座標同士の関係式を得たいと思う場合が、多いかと思われます。
つまり、\(Q_{i}\)が(9)式で求まるのであれば、\(P_{i}\)の関係式がほしいですよね。
その場合の変換式は、簡単に導くことができますので、紹介だけしておきましょう(^^)/
\(P_{i}\)の関係式がほしい
まず、(11)式に両辺\(\frac{\partial q_{i}}{\partial Q_{k}}\)を掛けて、\(i\)で和をとります。
つまり、
ところで、(13)式の右辺ですが、
と書くことができます。
※\(Q_{j}\)は変数としては、\(q\)しかありません。
※\(Q_{j}\)と\(Q_{k}\)は互いに独立なので、\(j=k\)の時だけ1になり、\(j\neq j\)の時は0になります。
(14)式を(13)式に代入しましょう。
そうすると、
右辺の和は、\(j=k\)の時しか残らないので、\(P\)については、
\(P_{j}=\sum_{i}\frac{\partial q_{i}}{\partial Q_{j}}p_{i}\)
となります。
添え字自体は本質ではないので、(9)式と添え字をそろえる為に\(i\)と\(j\)入れ替えておきましょう。
よって、
点変換による「新しい座標」と「新しい運動量」の関係式は、
\begin{align*}Q_{i}=f_{i}(\{q\},t)\cdot\cdot\cdot (9)\end{align*}
\begin{align*}P_{i}=\sum_{j}\frac{\partial q_{j}}{\partial Q_{i}}p_{j}\cdot\cdot\cdot (16)\end{align*}
と、このようになりました。