どうも(^^)/
前回は点変換についての記事を書いていきました。
↓こちらをご参考ください。
本記事では恒等変換というのを紹介したいと思います。
恒等変換を簡単に言うと、読んで字のごとく変換後も自分自身になるような変換のことを指します。
恒等変換とは
恒等変換のイメージは下記のような感じです。
正準変換が一般的な解析力学の枠組みの中での変数変換だとすると、点変換は正準変換の一部であり、恒等変換は点変換の一部であります。
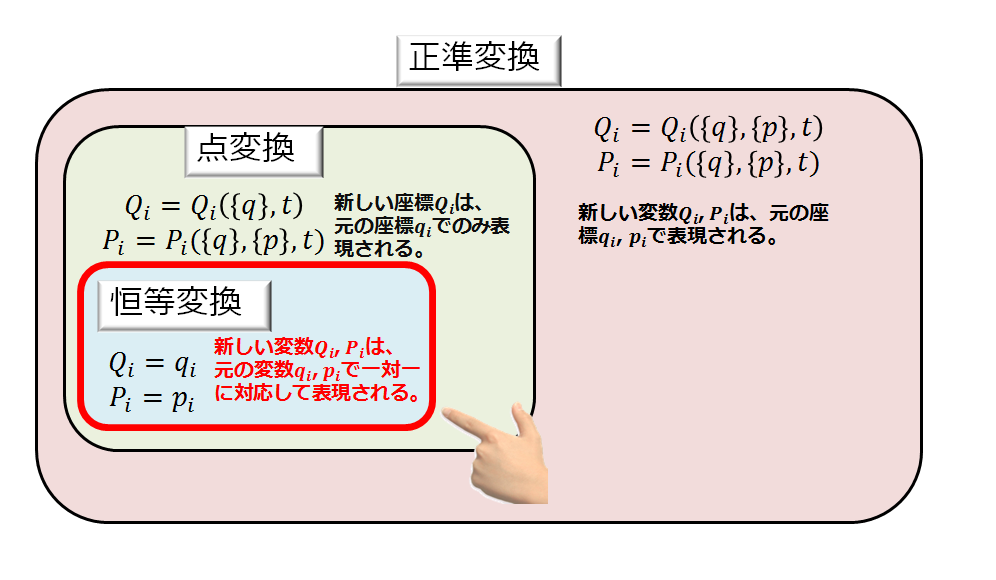
恒等変換は、上記の図のように、新しい変数\(Q_{i}\),\(P_{i}\)は元の変数\(q_{i}\),\(p_{i}\)で書けるような変換のことを言います。
つまり、恒等変換とは正準変換した後の新しい変数\(Q_{i}\),\(P_{i}\)は、
となるような変換であることを意味しています。
恒等変換の母関数の表記
恒等変換が点変換の一部であるということがわかれば、点変換の結果から恒等変換の結果を導くのが賢い方法ではないかと思いますので、まず点変換の母関数の表記を下記に記します。
※点変換:母関数による表記(第18.6報)をご参考にどうぞ。
点変換による母関数の表記は、下記のように、
\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}f_{i}(\{q\},t)P_{i}\cdot\cdot\cdot (3)\end{align*}
と書けます。点変換による「新しい座標」と「新しい運動量」の関係式
\begin{align*}Q_{i}=f_{i}(\{q\},t)\cdot\cdot\cdot (4)\end{align*}
\begin{align*}P_{i}=\sum_{j}\frac{\partial q_{j}}{\partial Q_{i}}p_{j}\cdot\cdot\cdot (5)\end{align*}
(1)式と(4)式を見比べると、恒等変換の表記にするためには、
とすれば良いことがわかります。
このときに、(5)式も計算しましょう。
和の部分が、\(i=j\)のみ残りその他は0になるので、
↑(2)式に帰着しました。
ということは、
母関数
\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}q_{i}P_{i}\cdot\cdot\cdot (7)\end{align*}点変換による「新しい座標」と「新しい運動量」の関係式
\begin{align*}Q_{i}=q_{i}\cdot\cdot\cdot (1)\end{align*}
\begin{align*}P_{i}=p_{i}\cdot\cdot\cdot (2)\end{align*}これの変換を恒等変換と呼びます。
恒等変換の意味
という変換を受けるということは、
(元の座標\(q_{i}\)、元の運動量\(p_{i}\))→(新しいの座標\(Q_{i}\)、新しいの運動量\(P_{i}\))
と変換されたことを意味しています。
これは、単純に「正準変数(\(q_{i},p_{i}\))が、微小時間に新たな正準変数(\(Q_{i},P_{i}\))になりながら位相空間を(ハミルトンの正準方程式を満足しながら)移動している」という見方ができます。
それを説明するために下記のような、位相空間(「座標-運動量」空間)で描くと・・・・・
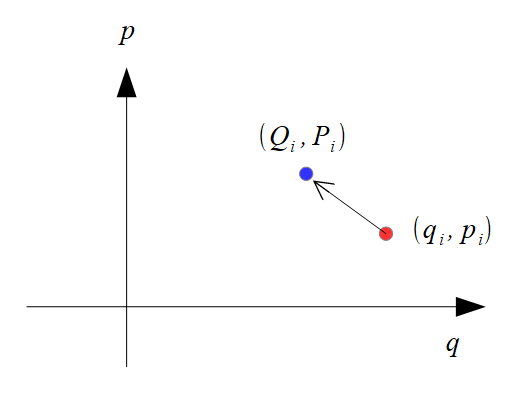
こんな感じでしょうか。
もちろん、(\(q_{i}\),\(p_{i}\))から(\(Q_{i}\),\(P_{i}\))への変換は正準変換なのですから、元の(座標、運動量)に対してもハミルトンの正準方程式を満足し、新しい(座標、運動量)についてもハミルトンの正準方程式を満足します。
※ここで、\(W_{2}\)は母関数で、
特に、母関数\(W_{2}\)が時間に陽に依存しないのであれば、(12)式は、
となるので、
ハミルトニアンを一定、すなわち「エネルギーを保存させながら位相空間上を●から●に点を移動している(状態を変化させている)」というように解釈することができます。
位相空間における状態点の変化も、時間による正準変換であると解釈することができるということですね(^^)
まとめ
恒等変換
”正準変換した後の新しい変数\(Q_{i}\),\(P_{i}\)”は、
\begin{align*}Q_{i}=q_{i}\cdot\cdot\cdot (1)\end{align*}
\begin{align*}P_{i}=p_{i}\cdot\cdot\cdot (2)\end{align*}のような変換を恒等変換と呼びます。
恒等変換は、「正準変数(\(q_{i},p_{i}\))が、微小時間に新たな正準変数(\(Q_{i},P_{i}\))になりながら位相空間を(ハミルトンの正準方程式を満足しながら)移動している」という見方ができます。