どうも(^^)/
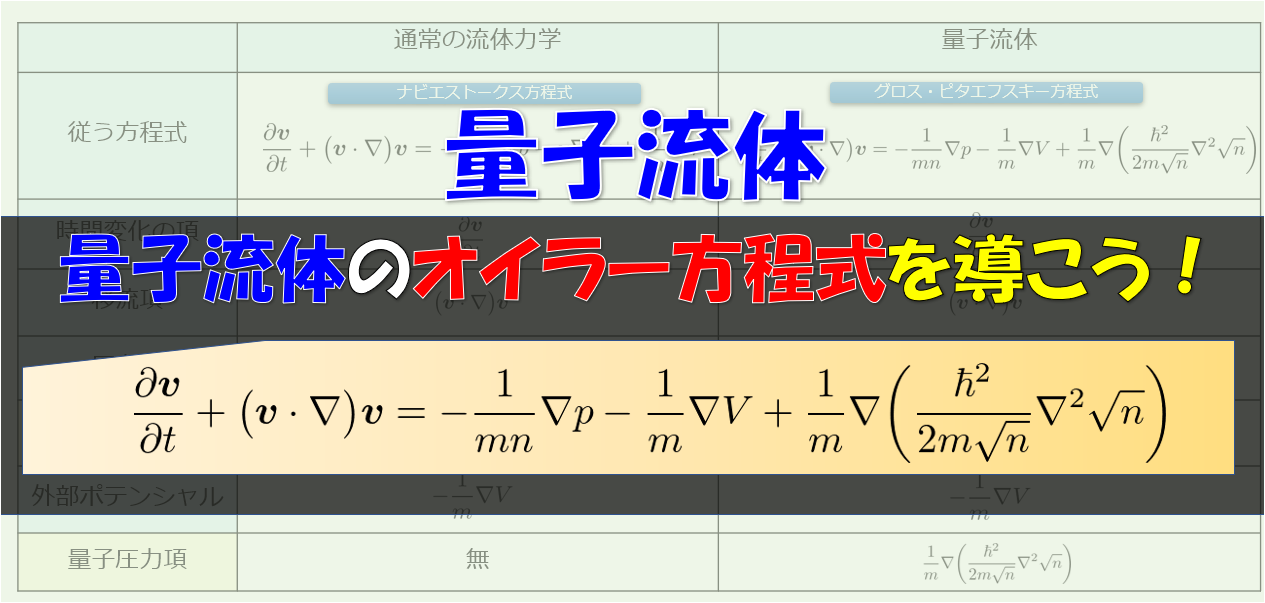
本記事では、量子力学的効果によって出現する量子流体が従う方程式であるグロス・ピタエフスキー方程式(非線形シュレディンガー方程式)から、流体力学でよく見られるような連続の式を導きたいと思います。
結論を先に示しておきます。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
連続の式
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0\tag{2}
\end{align*}
(1)式はともかく、(2)式は流体力学の「連続の式」ととてもよく似ているでしょ!!
(2)式の「連続の式」を(1)式のGP方程式から導出します。
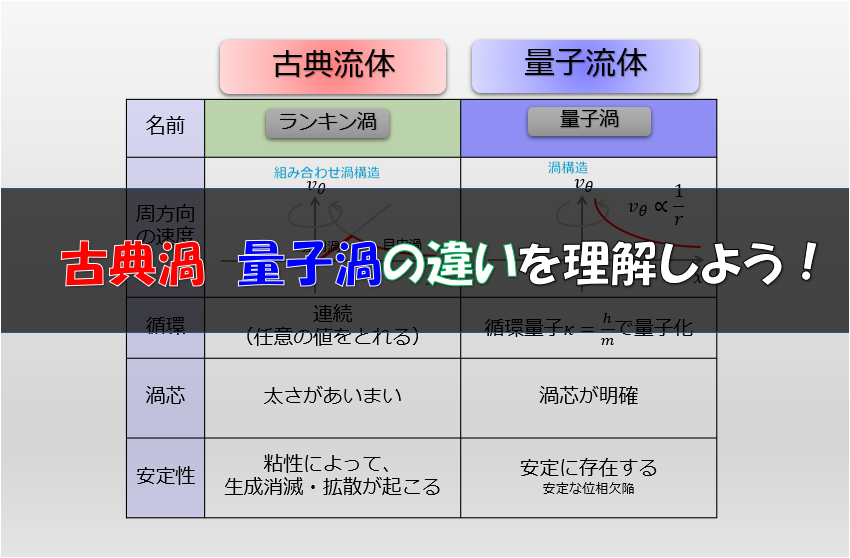
量子流体が(1)式のGP方程式に従うと言っても・・・”流体”と名を付けている以上はやはり通常の流体力学との類似性などが気になりますよね。
その類似性のひとつが、量子流体も連続の式が成り立つということです。
参考書
ボ-ズ・アインシュタイン凝縮 /吉岡書店/クリストファ-・ペシィック
前回の記事の復習
まずは前回の記事の復習をさらっとしたいと思います。
大多数のボース粒子が非常に小さい温度の場合に、量子力学的効果によって出現する流体は量子流体と呼ばれています。
量子流体は、低温状態で出現するボース・アインシュタイ凝縮によるものです。

ボース・アインシュタイ凝縮によって、最低エネルギー準位に大多数の粒子が落ち込むことにより、大多数の粒子を1つの波動関数(秩序変数)\(\psi(\boldsymbol{r})\)で記述でき、以下の方程式に従います。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
ただし、グロス・ピタエフスキー方程式は以下の状況を仮定していることに注意。
- ボース・アインシュタイ凝縮を起こしているので、大多数の粒子の状態をまとめて1つの波動関数\(\psi\)と書く。
- ボース・アインシュタイ凝縮を起こした大多数の粒子を捕獲ポテンシャルで捕獲する。
捕獲ポテンシャル:(\(V_{ext}=\frac{m\omega^2\boldsymbol{r}^2}{2}\)) - 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
Gross-Pitaevskii方程式から「連続の式」を導く
さて、GP方程式から連続の式を導いていきたいと思います。
出発点は、もちろんGP方程式です。
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{3}
\end{align*}
※変数\(\boldsymbol{r},t)\)があると、式変形が煩雑に見えますので、\(\psi(\boldsymbol{r},t)=\psi\)と表記することにします。
↓こんな感じです。
i\hbar\frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi+V_{ex}\psi(\boldsymbol{r},t)+g|\psi|^2\psi\tag{4}
\end{align*}
変数を書かないだけでだいぶすっきりとした見た目になったところで・・・・
では、連続の式を導いてみましょう!!
まずは、(4)式の複素共役の式を用意します。
-i\hbar\frac{\partial \psi^{*}}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi^{*}+V_{ex}\psi^{*}+g|\psi|^2\psi^{*}\tag{5}
\end{align*}
そして、(4)×\(\psi^{*}\)-(5)×\(\psi\)を計算して整理します。
煩雑なので、左辺と右辺を別々で計算してみましょうかね。
左辺
=i\hbar\frac{\partial \psi}{\partial t}\psi^{*}+i\hbar\frac{\partial \psi^{*}}{\partial t}\psi
=i\hbar\frac{\partial \psi\psi^{*}}{\partial t}=i\hbar\frac{\partial |\psi|^2}{\partial t}
\end{align*}
右辺
&=\bigg(-\frac{\hbar^2}{2m}\big(\nabla^2\psi\big)\psi^{*}+V_{ex}\psi\psi^{*}+g|\psi|^2\psi\psi^{*}\bigg)
-\bigg(-\frac{\hbar^2}{2m}\big(\nabla^2\psi^{*}\big)\psi+V_{ex}\psi^{*}\psi+g|\psi|^2\psi^{*}\psi\bigg)\\
&=-\frac{\hbar^2}{2m}\big(\psi^{*}\nabla^2\psi-\psi\nabla^2\psi^{*}\big)\\
&=-\frac{\hbar^2}{2m}\nabla\cdot\big(\psi^{*}\nabla\psi-\psi\nabla\psi^{*}\big)
\end{align*}
最後の式変形は、各自で試してみましょう(^^)/
というわけで、(左辺)=(右辺)とすることで、完成です。
\frac{\partial |\psi|^2}{\partial t}+\frac{\hbar}{2mi}\nabla\cdot\big(\psi^{*}\nabla\psi-\psi\nabla\psi^{*}\big)=0\tag{6}
\end{align*}
※量子力学をすでに学んだことがある人にとっては、別段目新しい式変形に見えないことでしょう。
(左辺)が単位時間当たりの\(|\psi|^2\)の変化ということになりますね。
\(|\psi|^2\)が低温状態の多体粒子で何を意味していたかというと、粒子数密度\(n=|\psi|^2\)を表しているのでした。
前の記事を読んでいない方は、↓こちらをどうぞ。
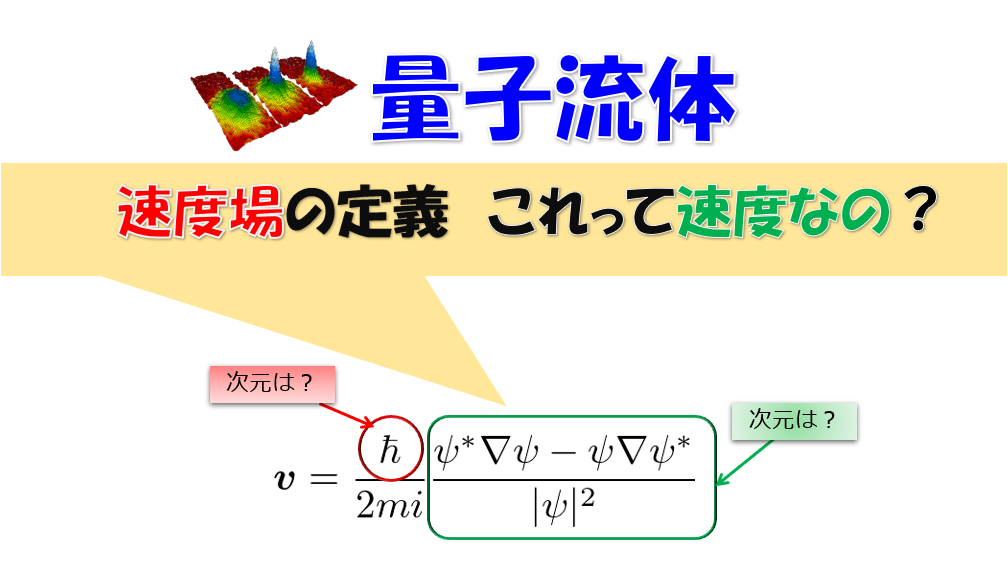
速度場を定義する
さて、ここで速度というのを定義してみます。
(左辺)が単位時間当たりの粒子数密度\(n=|\psi|^2\)の変化を表しているであれば、その他の項はそれをもたらした原因というふうに解釈できます。
速度場の定義
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\tag{7}
\end{align*}
※もちろん、\(\boldsymbol{v}=\boldsymbol{v}(\boldsymbol(r),t)\)です。
とこのように定義します。
そうすると、粒子数密度を\(n=|\psi|^2\)と置くことにより、
連続の式
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0\tag{8}
\end{align*}
連続の式が導くことができました。
これが量子流体が従う連続の式ということになります。
本当に、(7)式が速度場とおいても良いのかと疑問に思われるかもしれませんが、少なくとも速度場というからには(7)式が速度の次元を持っているということを確認できれば、(7)式は速度場と考えても良いでしょう。
各自で(7)式の次元を確認してみると良いでしょう。
速度場は位相の勾配で記述できる
大多数の粒子を秩序変数\(\psi\)で記述できるということを前回の記事で示しました。
そこで、\(\psi\)をより一般的な複素数関数で以下のように書けるとします。
\psi=\sqrt{n}e^{i\theta}\tag{8}
\end{align*}
一般的な複素関数を絶対値の大きさの部分と位相の部分に分けて書いただけですが、それぞれに意味があります。
- \(\sqrt{n}\)は粒子数密度に関係した量:$(n=|\psi|^2)$
- \(\theta\)は速度場に関係した量←本項の内容
先ほど、(7)式で速度場を定義できたのですから、
(7)式に(8)式を代入して、速度場がどのように記述されるのかを見ておきましょう。
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\tag{8}
\end{align*}
を丁寧に計算していきます。
\nabla \psi=\big(\sqrt{n}\big)e^{i\theta}+\sqrt{n}i\big(\nabla\theta\big)e^{i\theta}
\end{align*}
\nabla \psi^{*}=\big(\sqrt{n}\big)e^{-i\theta}-\sqrt{n}i\big(\nabla\theta\big)e^{-i\theta}
\end{align*}
となるので、
&\psi^{*}\nabla\psi-\psi\nabla\psi^{*}\\
&=\bigg(\big(\sqrt{n}\big)e^{i\theta}+\sqrt{n}i\big(\nabla\theta\big)e^{i\theta}\bigg)\sqrt{n}e^{i\theta}-\bigg(\big(\sqrt{n}\big)e^{-i\theta}-\sqrt{n}i\big(\nabla\theta\big)e^{-i\theta}\bigg)\sqrt{n}e^{-i\theta}\\
&=2ni\nabla\theta
\end{align*}
ですので、速度場は、
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{2ni}{n}\nabla\theta=\frac{\hbar}{m}\nabla\theta\tag{9}
\end{align*}
となりました(^^)/
量子流体での速度場は通常の流体よりもかなり制限が厳しい?
速度場が位相の勾配
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{10}
\end{align*}
で記述できるということを示しましたが、これはかなり厳しい制限があるということになります。なぜなら、(10)式の両辺にナブラ演算子\(\nabla\)の外積を作用させて、渦度\(\boldsymbol{\omega}=\nabla\times \boldsymbol{v}\)を作ろうとすると、
\boldsymbol{\omega}=\nabla\times \boldsymbol{v}=\frac{\hbar}{m}\nabla\times\nabla\theta=0\tag{11}
\end{align*}
となります。
これは、\(\theta\)が微分可能な関数であれば常に渦度\(\boldsymbol{\omega}\)は0、つまり渦無し流れになるということを意味しています。
通常の流体であれば、粘性によって渦度は0であったしても、渦度が突然出現するなんてことがあるのですが、量子流体の場合はそれがないと言っているのです・・・・
が、しかし、\(\theta\)が微分可能な関数でなくて、特異な点が合った場合はどうなるのでしょうか?
それは、(11)式が成り立つ保証はなくなるので、渦度が必ず0というわけではなく、渦度が出現する可能性があるということになります。
※これは、量子流体で出現する量子渦を示唆しています
まとめ
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
から、凝縮体の波動関数(秩序変数)を\(\psi=\sqrt{n}e^{i\theta}\)とおき、速度場を、
速度場
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{10}
\end{align*}
と定義することにより、以下のような連続の式を導出することができました。
連続の式
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0\tag{8}
\end{align*}
わかりやすい論文も見つけたので、↓こちらもどうぞ
The Gross-Pitaevskii Equation and Bose-Einstein condensates