こんにちは(@t_kun_kamakiri)。
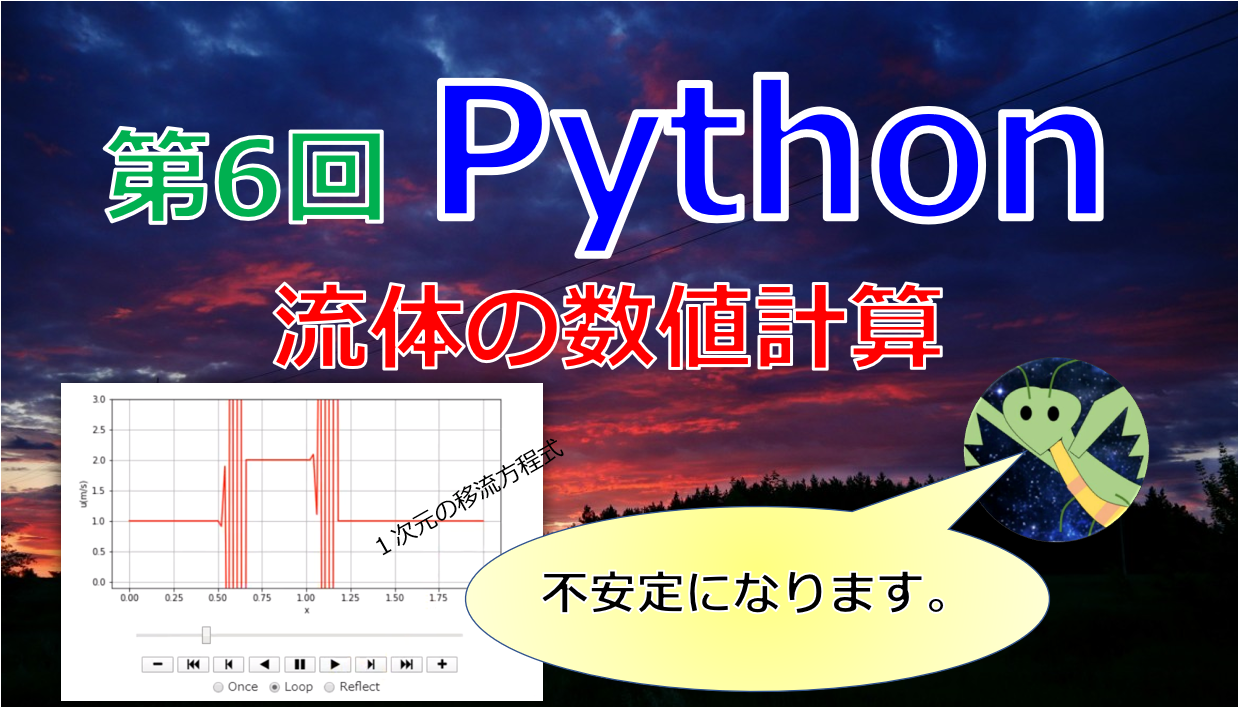
今回は、Pythonを使って「１次元の移流方程式」のクーラン条件のお話をします。
クーラン条件は数値的安定性とも関係があるので、必ず学んでおいた方が良いですね。
本記事では、わざと数値的に不安定な状態での数値計算もやりますので、解の振る舞いがどのようになるのかを確認しながら見ていただければと思います。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
☟前回の記事がまだの人はこちらから
移流方程式における安定性条件（クーラン条件）を考える。
前回作成した全体のコード：１次元移流方程式
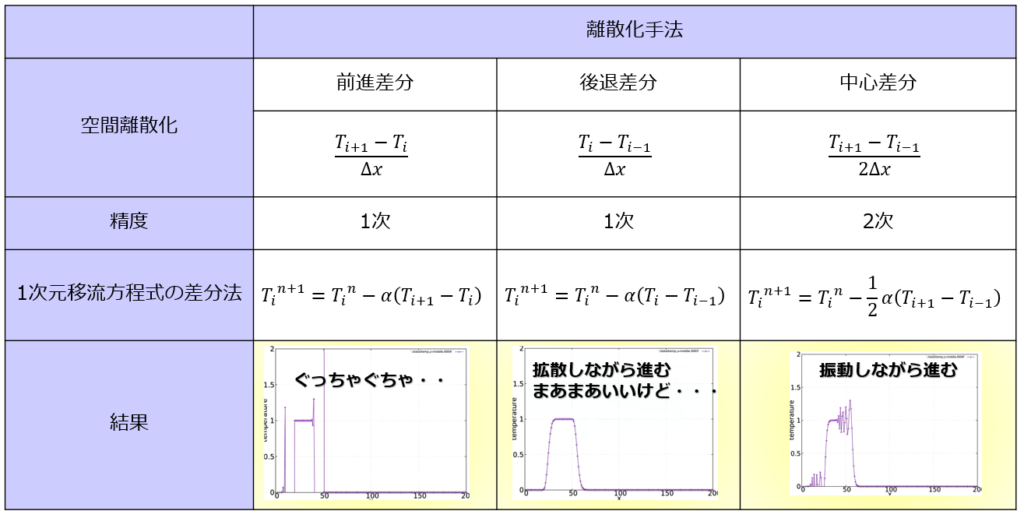
前回は、１次元移流方程式を後退差分で解くプログラムをPythonで書きました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML nx = 41 dx = 2 / (nx-1) nt = 25 c = 1 dt = .025 x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) plt.grid() plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) rc('animation', html='jshtml') plt.close() anim |
解いている方程式は、
１次元移流方程式の離散化（後退差分）
u^{n+1}_{i}=u^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(u^{n}_{i}-u^{n}_{i-1}\big)\tag{1}
\end{align*}
です。
数値的安定性
(１)式を離散化して、時々刻々と変動する数値解を安定的求めるには、計算を進めるにあたって数値的な誤差が増大しないことが条件になります。
移流方程式には厳密解が存在するので、厳密解をとして\(\tilde{u}^{n}_{i}\)、数値解を\({u}^{n}_{i}\)とします。
そうすると、厳密解と数値解には誤差があるので誤差を\(\tilde{\epsilon}^{n}_{i}\)と置いておきしょう。
u^{n}_{i}=\tilde{u}^{n}_{i}+\tilde{\epsilon}^{n}_{i}\tag{2}
\end{align*}
(2)式を(１)式に代入します。
\tilde{u}^{n+1}_{i}+\tilde{\epsilon}^{n+1}_{i}&=\tilde{u}^{n}_{i}+\tilde{\epsilon}^{n}_{i}\\
&-\frac{c\Delta t}{\Delta x}\big(\tilde{u}^{n}_{i}-\tilde{u}^{n}_{i-1}\big)\\
&-\frac{c\Delta t}{\Delta x}\big(\tilde{\epsilon}^{n}_{i}-\tilde{\epsilon}^{n}_{i-1}\big)\tag{3}
\end{align*}
じゃっかんごちゃごちゃしてしまいましたが、\(\tilde{u}^{n}_{i}\)は厳密解なのですからそもそも、
\tilde{u}^{n+1}_{i}=\tilde{u}^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(\tilde{u}^{n}_{i}-\tilde{u}^{n}_{i-1}\big)
\end{align*}
を満たしています。
移流方程式が線形な方程式であるため、線形解である\(u^{n}_{i}=\tilde{u}^{n}_{i}+\tilde{\epsilon}^{n}_{i}\)のうちの右辺のどちらも移流方程式を満たすという事です。
今、考えるべきは以下の式です。
\tilde{\epsilon}^{n+1}_{i}=\tilde{\epsilon}^{n}_{i}-\frac{c\Delta t}{\Delta x}\big(\tilde{\epsilon}^{n}_{i}-\tilde{\epsilon}^{n}_{i-1}\big)\tag{4}
\end{align*}
(4)式は厳密解というよりは、そもそも誤差なので\(\tilde{\epsilon}^{n}_{i}=0\)の予定ですが、(4)式がある以上はこの式に従ってもらいながら発散されるととても困ることになります・・・・
この誤差\(\tilde{\epsilon}^{n}_{i}\)が時間とともに増大するかどうかを考えて、増大するような数値解法だと解が不安定になるというわけです。
例えば、以下のようにまとめると数値的安定性条件が出てきそうなのがわかります。
\tilde{\epsilon}^{n+1}_{i}=\bigg(1-\frac{c\Delta t}{\Delta x}\bigg)\tilde{\epsilon}^{n}_{i}+\tilde{\epsilon}^{n}_{i-1}\tag{4-1}
\end{align*}
この式を見たときに、
1-\frac{c\Delta t}{\Delta x}\geq 0
\end{align*}
じゃないと、解が安定しないのではないかというのが予想できます。
なぜなら、(4-1)式の左辺は「n+1ステップ」の「格子点i」での誤差に対して、右辺は「nステップ」の「格子点iとi-1」の誤差です。
あるステップのときのある場所ではマイナスの値をとったりプラスの値を取ったりして解が不連続になりやすいと予想できます。
そうすると、不連続点の位置での微分は値が発散するということになるので（今は離散化しているのでせいぜい大きな値をとるくらい）、解が不安定になりやすい・・・・とちょっぴり予想できます。
フォン・ノイマンのフーリエ解析法
今回使う方法は、「フォン・ノイマンのフーリエ解析法」と呼ばれるものです。
名前だけで圧倒されそうな解法ですが、ポイントは以下となります。
【ポイント】
- 関数を波に分解→フーリエ変換（or フーリエ級数展開）
- 時間が経つと波の振幅が大きくなる（大きくなると不安定）
フーリエ変換の簡単なお話をしておきましょう(^^)/
関数を波に分解→フーリエ変換（or フーリエ級数展開）
フーリエ変換は下記のようにある関数\(f(x)\)を、\(\sin\)波や\(\cos\)波や正弦波\(e^{ikx}\)などの様々な異なる波数の波に分解して波の空間（波数空間）に変換する方法のことです。
どんな関数も異なる波数の\(\sin\)波の和で書いてやるのです。↓こんな感じです。
※以下の場合は周期関数\(f(x)\)に関して、例を挙げています。
こうやって考えると、「おや？\(\sin2\pi x\)(周期１)の波が1個か・・・・\(\sin10\pi x\)(周期１/10)の波が10個か・・・」と、波のくせに数えれるという恩恵を受けることができます。
- 「1個、10個、3個」とか書いたものがフーリエ変換（or フーリエ級数展開）した後の関数（波数空間での関数）のこと
- 「1個、10個、3個」は各波数の波の振幅
と考えることができます。
- 結局複雑な波形でも、ある波数を持つ波の重み付けによる重ね合わせで表現できるのです。
つまり、数値的に不安定な解とはこういうことです。
誤差\(\tilde{\epsilon}^{n}_{i}\)をフーリエ級数展開して、ある波数の波が増大する可能性があるのかどうかを調べることで、解の安定性条件が導くことができます。
フーリエ変換について学びたい方は☟こちらからどうぞ！
時間が経つと波の振幅が大きくなる（大きくなると不安定）
誤差\(\tilde{\epsilon}^{n}_{i}\)、時刻\(n\)ステップと格子点\(i\)で以下のようにフーリエ級数展開を行います。
\tilde{\epsilon}^{n}_{i}=\sum A^{n}_{k}e^{Ik(i\Delta x)}\tag{5}
\end{align*}
これは、波数\(k\)の波\(e^{Ik(i\Delta x)}\)が\(A^{n}_{k}\)で重み付けされた形になっています。
※虚数は、格子点の\(i\)と紛らわしいので「虚数\(I\)」と表記しました。
これを(4)式に代入します。
(４)式は線形な方程式なので(5)式の和のほとんどは書かなくてもよくなります。
A^{n+1}_{k}=A^{n}_{k}-\alpha\bigg(A^{n}_{k}-A^{n}_{k}e^{-Ik(i\Delta x)}\bigg)\tag{6}
\end{align*}
※\(\alpha=\frac{c\Delta t}{\Delta x}\)と置いています。
これを今、以下のようにまとめます。
g& = \frac{A^{n+1}_{k}}{A^{n}_{k}}\\
& =1-\alpha\bigg(1-e^{-Ik(i\Delta x)}\bigg)\\
& = 1-2\alpha\sin^2\frac{\phi}{2}-I\alpha\sin\phi\\
& = x+yI
\end{align*}
※実部と虚部に分けました。
※\(\phi=Ik\Delta x\)と置きました。
だから、
|g|=\bigg(4\sin^2\frac{\phi}{2}\big(\alpha-\frac{1}{2}\big)-\sin^2\frac{\phi}{2}+1\bigg)\tag{7}
\end{align*}
となります。
ちょっとわかりにくいので絵でイメージすると以下のようになります。
\(g = \frac{A^{n+1}_{k}}{A^{n}_{k}}\)が１より大きいという事は、ある波数\(k\)の重みがどんどん増大してやがて数値的には無視できないくらいの誤差になるということを意味しています。
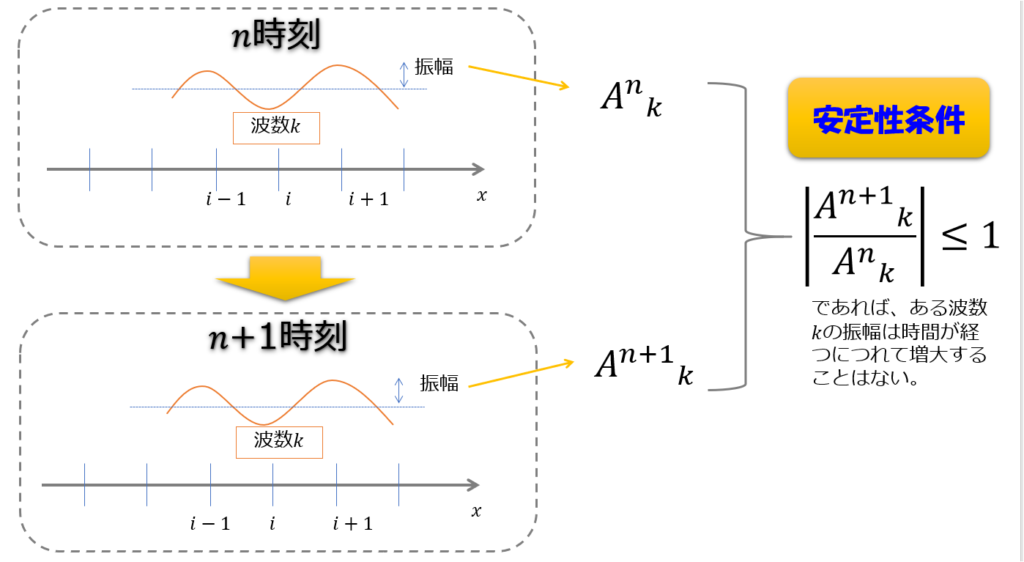
つまり、「n+1ステップでの波数\(k\)の重み」と「nステップでの波数\(k\)の重み」\(g = \frac{A^{n+1}_{k}}{A^{n}_{k}}\)を考えたときに、
\left\{\begin{matrix}
g\leq 1\,\,\,\,(安定)\\
g> 1\,\,\,\,(不安定)
\end{matrix}\right.
\end{align*}
という判別ができます。
じゃー、変数\(\alpha\)として\(g\)のグラフを描いて\(g\leq 1\)となる条件を導けばよいという事になります。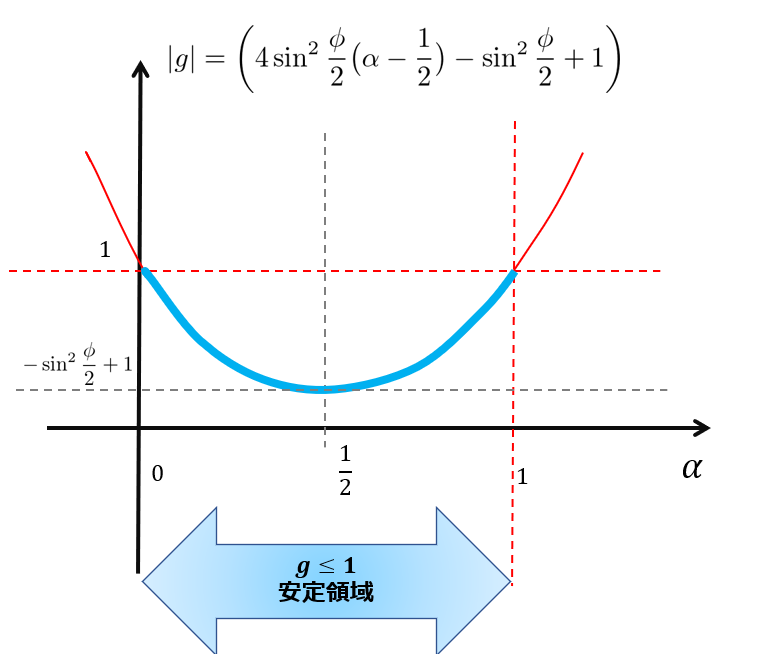
２次関数のグラフを描いて安定領域を探せば、
0\leq \alpha \leq 1
\end{align*}
すなわち、
0\leq \frac{c\Delta t}{\Delta x}\leq 1\tag{8}
\end{align*}
となります。
(８)式を満たせば、\(|g|\leq 1\)を満たしますね。
先に予想していたような結果を得ることができました。
ちなみに(８)式をクーラン条件といいますので覚えておきましょう(^^)/
\(\alpha=\frac{c\Delta t}{\Delta x}\)をクーラン数といいます。
では、クーラン数の値を変えてシミュレーションをしてみましょう。
クーラン数を「\(\alpha=\)0.5、1、1.5」と変えてシミュレーション
以下の３パターンで解析をします。
| \(\alpha\) | 解の振る舞い |
| 0.5 | ？ |
| 1.0 | ？ |
| 1.5 | ？ |
Pythonコードを書きます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | import numpy as np import matplotlib.pyplot as plt from matplotlib import animation, rc from IPython.display import HTML nx = 101 dx = 2 / (nx-1) nt = 25 c = 1 alpha = 1.0 dt = alpha * (dx/c) print('dx=',dx) print('dt=',dt) x = np.linspace(0,2,nx) un = [] u = np.ones(nx) u[int(.5 / dx):int(1 / dx + 1)] = 2 fig = plt.figure(figsize=(8,4)) ims=[] for n in range(nt): un = u.copy() if (nt%1==0): im = plt.plot(x,u, "r") ims.append(im) for i in range(1, nx): u[i] = un[i] - c * dt / dx * (un[i] - un[i-1]) plt.grid() plt.ylim([-0.5,3]) plt.xlabel("x") plt.ylabel("u(m/s)") anim = animation.ArtistAnimation(fig, ims) rc('animation', html='jshtml') anim |
ここから\(\alpha\)の値を変えて、アニメーションを見てみます。
\(\alpha =0.5\)
この条件は、クーラン条件からすると安定的に解ける条件のはずですがどうなるでしょうか。
☟動画を見てください。
解が安定はしていますが、「+x方向に進みながら波形の形が変わっている」という結果でした。
\(\alpha =1.0\)
続いて・・・
この条件は、クーラン条件からすると安定的に解ける条件のはずですがどうなるでしょうか。
☟動画を見てください。
おや(/・ω・)/
安定的に解けてるし、「+x方向に形を変えずに進んでいる・・・」！
\(\alpha =1.5\)
これはどうでしょうか？
この条件は、クーラン条件からすると不安定な解の振る舞いをする条件のはずですがどうなるでしょうか。
☟動画を見てください。
動画を見ると、みごとにめちゃくちゃな解の振る舞いをしてしまいました！！
結果まとめ
| \(\alpha\) | 解の振る舞い |
| 0.5 | 安定 形が変わって進む |
| 1.0 | 安定 形が変わらず |
| 1.5 | 不安定 見てられない |
\left\{\begin{matrix}
g\leq 1\,\,\,\,(安定)\\
g> 1\,\,\,\,(不安定)
\end{matrix}\right.
\end{align*}
の条件と一致している数値計算の結果ですね。
まとめ
本記事の内容は「\(\alpha>0\)かつ後退差分をした際」の安定条件が、
0\leq \frac{c\Delta t}{\Delta x}\leq 1\tag{8}
\end{align*}
となることを示しました。
(８)式をクーラン条件といいます。
ここで注意しておきたいのは、本記事の内容は「\(\alpha>0\)かつ後退差分をした際」の安定条件についてですが、
\(\alpha<0\)である場合に関しては、後退差分ではいかなる条件も不安定な解の振る舞いをします。
もし、\(\alpha<0\)の条件で数値計算を行うのであれば前進差分で解く方が安定性が良いです。
それは以下の記事でもまとめていますので、良ければ参考にしてください。
コード自体はFortranを使用していますが、コードは無視して動画を見るだけでも勉強になると思います。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
（本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません）
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと！！って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学１年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値計算を勉強したい方
それをいかに誤差が少なく、安定的に解くかがカギになっており、数値的解法は多く提案されています。
Follow @t_kun_kamakiri