【ガリレイの相対性原理】解析力学で考える。

どうも(^^)/

前回の内容では最小作用の原理からラグランジュ方程式の導出を行ったのでした。

前回の記事がまだお読みでない方は是非お読みください。

本記事の内容は以下となっております。

本記事の内容では、とても簡単なお話しかしません。

内容は基本的に、「ランダウ＝リフシッツの”力学”」の内容になりますが、可能な限り補足をしていきたいと思います。

力学 (増訂第3版) ランダウ=リフシッツ理論物理学教程

エリ・ランダウ, イェ・エム・リフシッツ

3,860円(04/27 14:44時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

解析力学を学ぶにあたってお勧めの参考書を記事の後半に紹介しておきます。

ガリレイの相対性原理

「ガリレイの相対性原理」という名前は、どこかで聞いたことがあるかもしれません。

さらっと言ってしまうのであれば、

めちゃめちゃ回りくどい言い方だな～って思いませんかね。

確かに地球の座標系に対して、ニュートンの第二法則\(m\boldsymbol{a}=\boldsymbol{f}\)が成り立っているとしていますが、

その地球の座標系は本当に慣性系でしょうか？

慣性系かどうかはわかりませんが、結果として慣性の法則が成立している系だとしたら・・・というのがやはりニュアンスで含めた方が良いと思ったのです。

とは言え、ガリレイの相対性原理はとても簡単です。

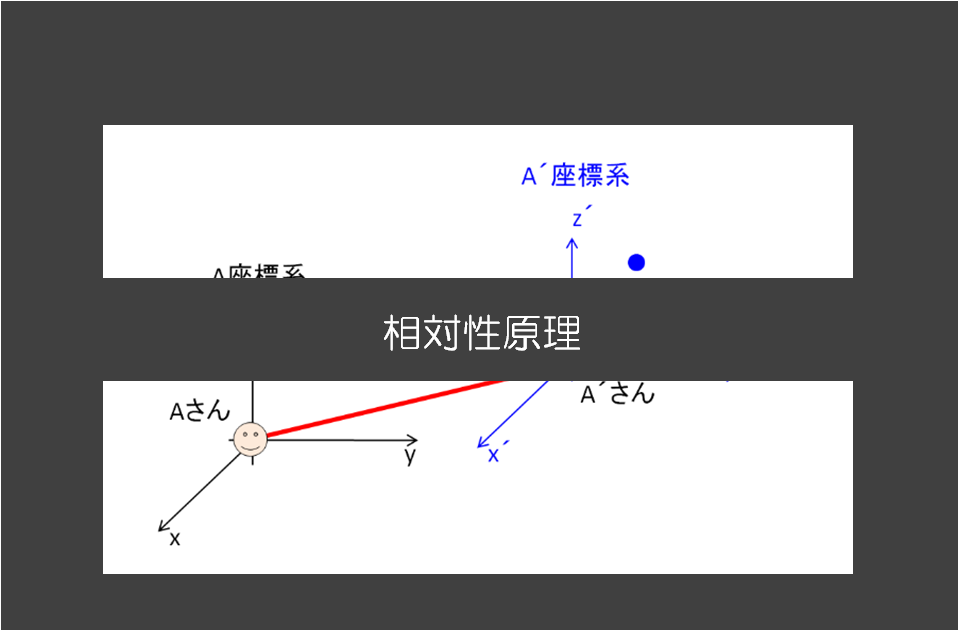
以下の絵ですぐにわかります。

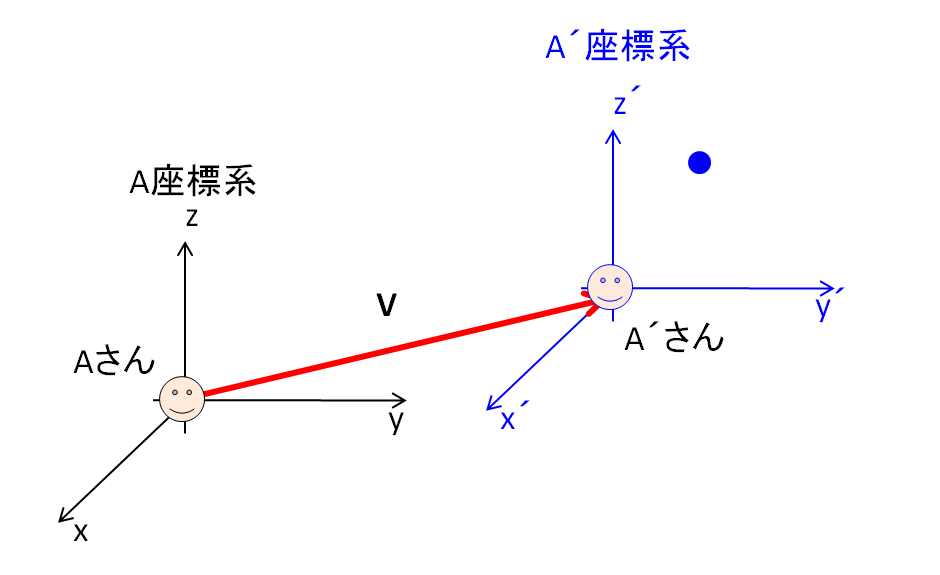
「\(A\)さんの慣性座標系」と「\(A\)さんの慣性座標系に対して\(\bf{V}\)で動いている\({A}’\)さんの座標系」を考えます。

本当にそうなのか、さくっと見てみましょう！！(^^)/

\(A\)さんの座標系での運動方程式

即答でこちらですね!(^^)!

※\(\boldsymbol{f}\)は絵の●に働く力（何でも良いでしょう）

\({A}’\)さんの座標系での運動方程式

\({A}’\)さんの座標系から見ると、質点の座標は

と、このようになりますね。

そうすると(2)を(1)に代入すると、\(\boldsymbol{V}\)は時間に対しては一定なので、

となります。

「おー！！(1)式と(3)式の形（物理法則）が座標系によらないじゃないかー！」

というのがガリレイの相対性原理と言うのです。

そして、(2)式の変換に対して物理法則の変更がないことを、「ガリレイ変換に対して不変」と言います。

めちゃくちゃ基礎で大変恐縮です(笑)
ただ、ランダウ＝リフシッツの”力学”ではもう少しこのへんをごちゃごちゃ言っておりますね(笑)

(2)式の変換は本当にそうか？

(2)式の座標変換をさらっと流しましたが、果たして座標変換に対して(2)式はそうなでしょうか？

重要な仮定が入っておりますね。

それは、

「時間というものが座標によらず絶対的なものであるということ」です。

なので本当は(2)式に加えて、

としなければなりません。

しかし・・・・

相対性理論を学んだ方であれば、時間は絶対的なものではないということを知っていることと思います。

詳細は延べませんが、光の速度に近い速度で動く座標系に対しては、>>ローレンツ変換が成り立っているとしています。
ご興味があるかたは、電磁気学でとても有名な「マクスウェル方程式」に対してガリレイ変換をしてみてください。
全然違う形になります(笑)
つまり、マクスウェル方程式に対して「ガリレイ変換は不変でない」という結論になります。

相対性理論の範疇では、座標系によって空間は伸び縮みしますし、時間は遅くなったりもします。
なので、「適当な基準系をとると、運動法則は違った形をとり複雑になる」と色々とランダウさんは文面で言っておられますね。

相対性理論とは違いますが、上記の文面に対しては、
例えば下記のように、電車が加速度\(a_{1}\)で動き始めている状況を考えてイメージすることができます。
電車内と電車の外での「つり革の運動方程式」を考えるのです。

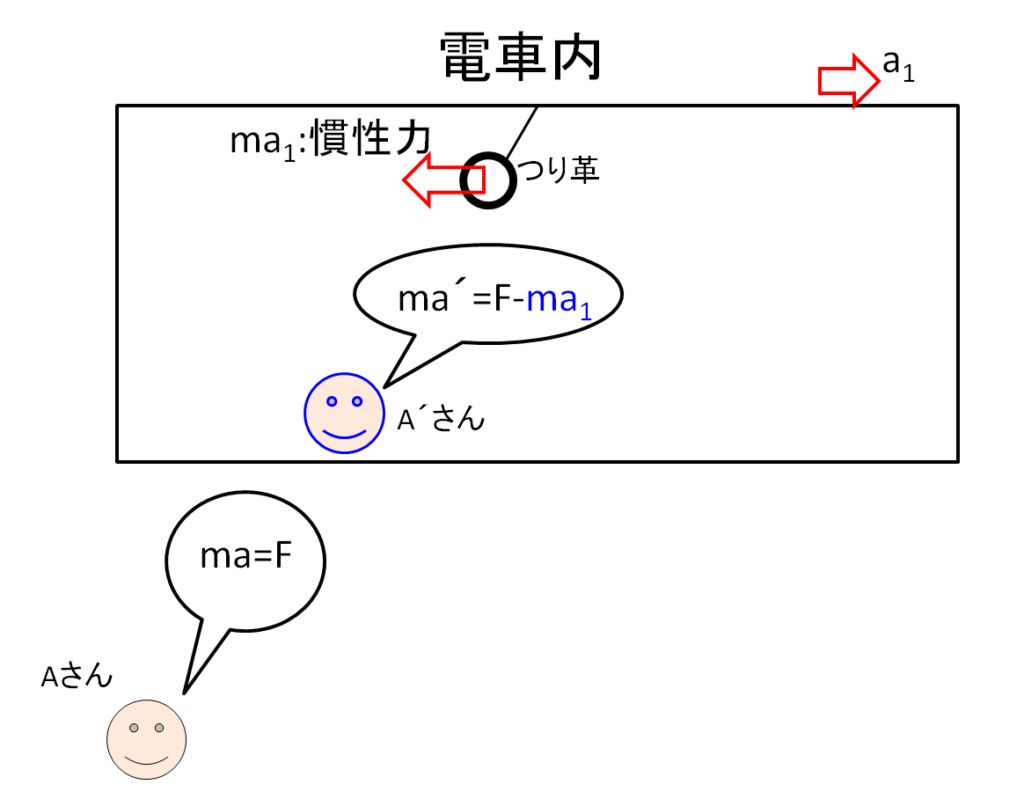
電車外にいる\(A\)さんにとってつり革を見れば相変わらず運動方程式は

だと言うでしょう。

しかし、

電車内にいる、\({A}’\)さんが見ればつり革は”力を加えられていない”のに電車とは逆方向に動き出すのです。
高校物理を習った方は、これを慣性力と言うことをご存知かと思います。

\({A}’\)さんから見れば運動方程式は、

と言うでしょう。

あら不思議(笑)

\(A\)さんから見た運動方程式と違う形になっちゃったよ。。。

と、こうなるのですが、
「この電車内での座標系を慣性系としたならば、その座標系に対して一定速度で動いている座標系に対しては運動方程式の記述は変わらないだろうね」

ということが言えますね（たぶん）。

だからどの座標系を基準にとるかが非常に重要になります。

この辺の議論は相対性理論と絡めないとなかなか説明しづらいところです。

ラグランジアン\(L\)は速度\(\dot{q}^2\)のみに依存？

慣性系のお話をしたら、次のようなことが言えるはずです。

ラグランジアン\(L(q,\dot{q},t)\)は一般座標\(q\)、一般速度\(\dot{q}\)、時間\(t\)を変数としていましたが、

自由に運動している質点を考えた場合、慣性系においては空間・時間が一様、つまり

っていうことであれば、ラグランジアン\(L(q,\dot{q},t)\)は、座標と時間に対してあらわに変数として含まないはずです。

なので、ラグランジアン\(L(\dot{q})\)のように、一般速度\(\dot{q}\)のみの関数のはずです。

さらに、空間が等方的であるということは向きがないのです。

ランダウさんは、「空間が等方的である！！だからラグランジアン\(L\)は、速度\(\dot{q}\)は絶対値\(\dot{q}^2\)のはずだ！」みたいな感じで言っておられますな。。。

まあ、それでも良いと思われます。

僕が偉そうに言っても仕方ないことですが、ラグランジアン\(L\)が少なくとも\(\dot{q}^2\)みたいな形でないといけないことは、

最小作用の原理でもイメージができます。

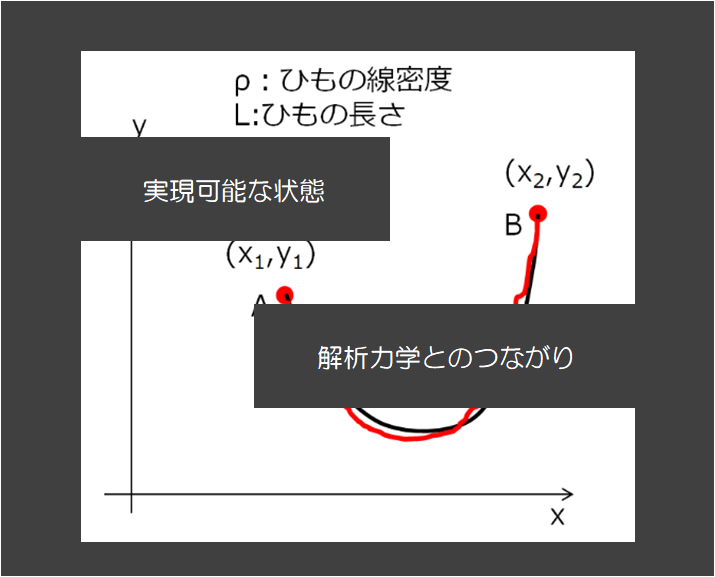
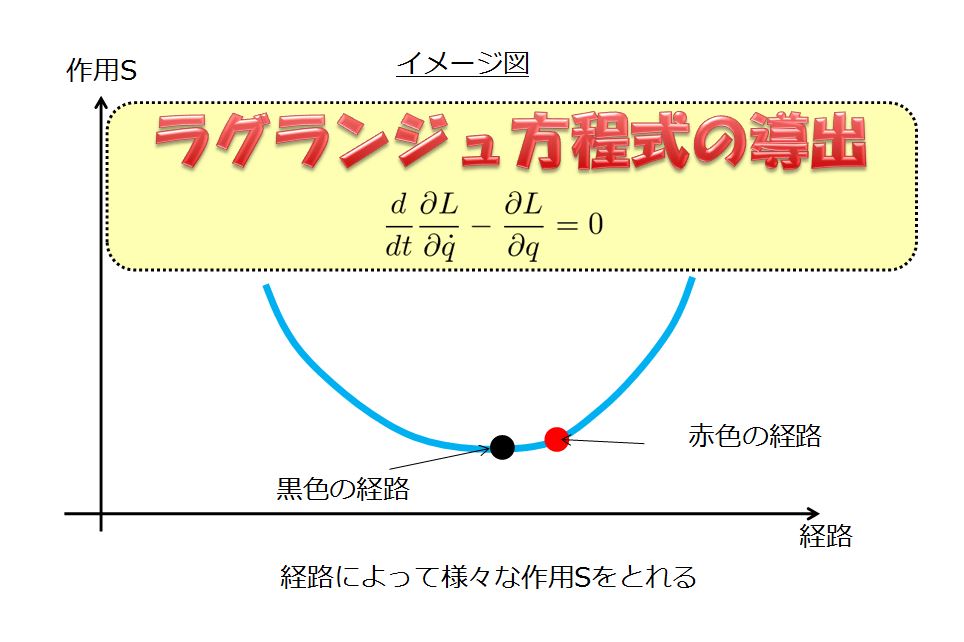
下記の絵を思い出しましょう。

お読みでない方は、こちらをどうぞ♪

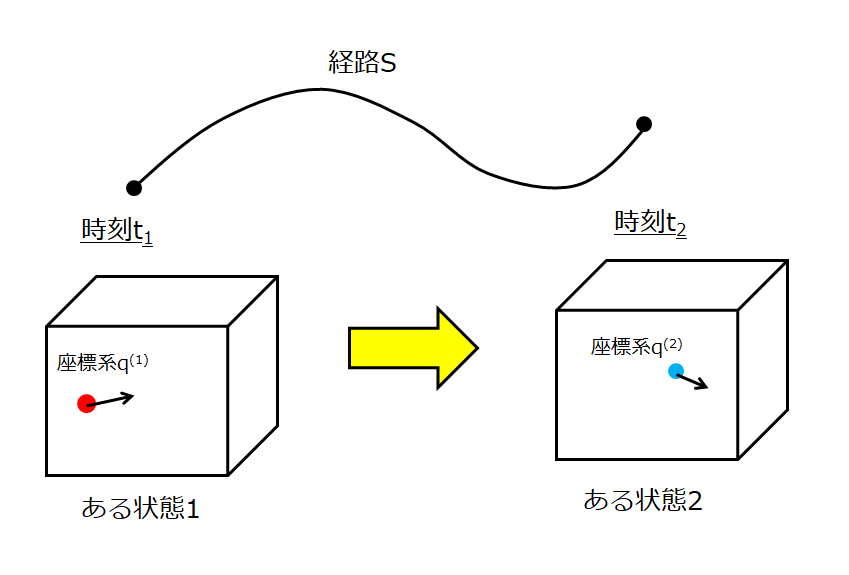
上の絵のようにあ、”状態”　経路みたいなものを考えるのでしたね。

それを式で書くならば、

\begin{align*}S=\int_{t_{1}}^{t_{2}}L(q,\dot{q},t)dt\)

とこのようになり、実現可能な状態というのは作用\(S\)を最小にした状態であり、そこからラグランジュ方程式を導いたのでした。

「最小にする」というキーワードがとても重要です。

\begin{align*}L=\dot{q}\end{align*}

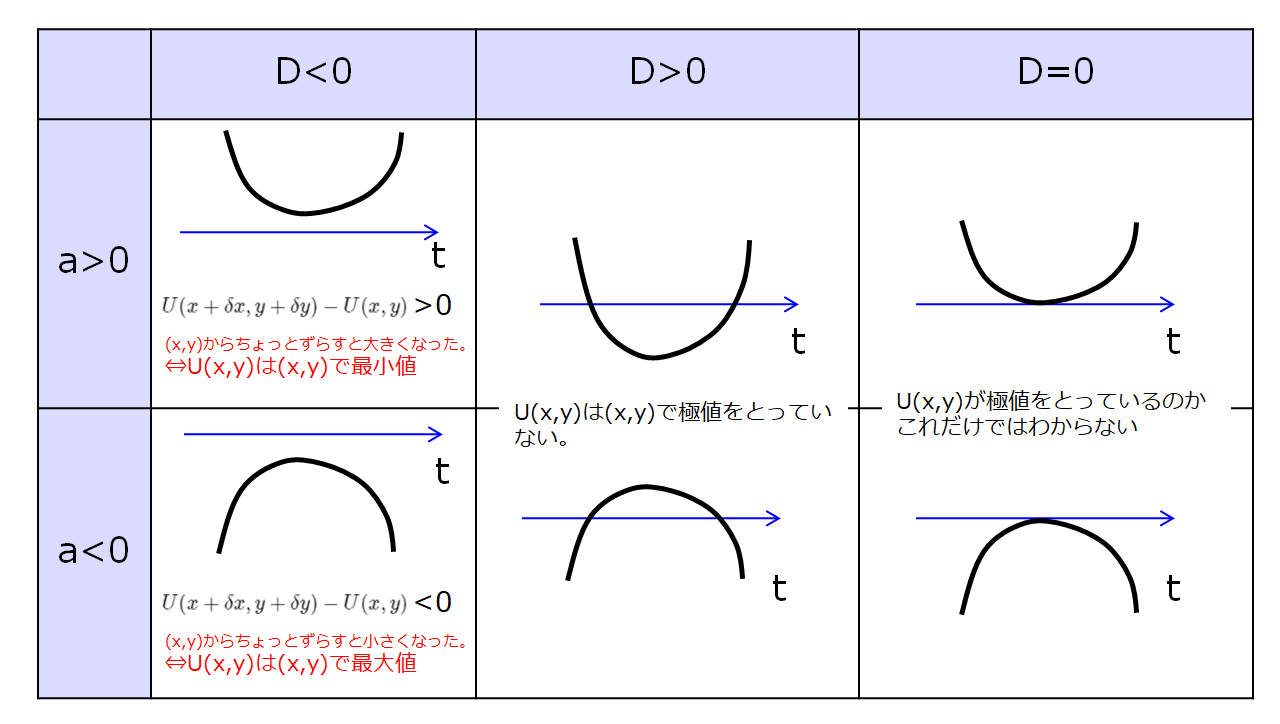
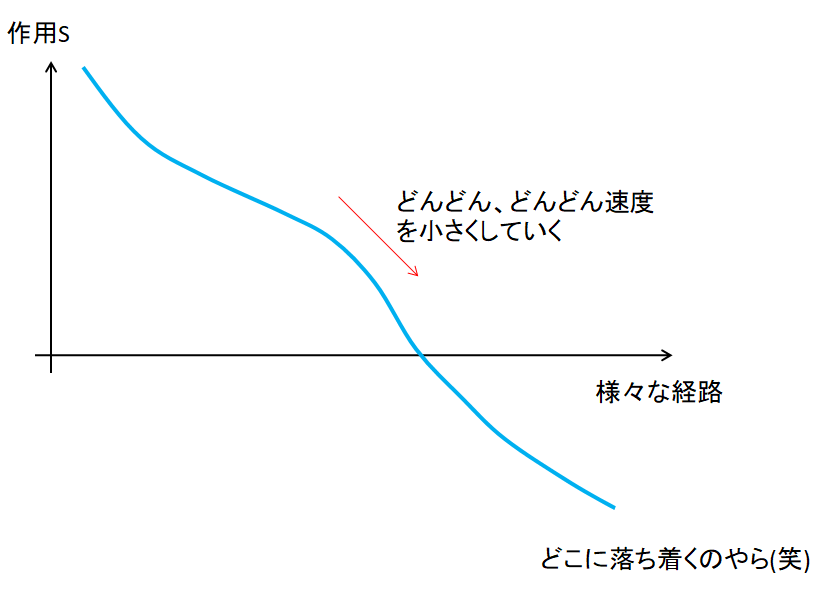
みたいな形だとどうなりますかね。

\begin{align*}S=\int_{t_{1}}^{t_{2}}L(\dot{q})dt=\int_{t_{1}}^{t_{2}}\dot{q}dt\end{align*}

これじゃー、

「え、ラッキー♪\(\dot{q}\)がマイナスだったらどんどんSの値小さくできるじゃないか～♪」

と言って、状態が定まりません(笑)

↓こんな感じです(笑)

イメージ図

 

なので、ラグランジアン\(L(\dot{q})\)は、少なくとも速度に対しては\(\dot{q}^2\)の”ような”形でないといけない。

あくまで、”ような”なんですよね～。

\begin{align*}\dot{q}^4\)、\(\dot{q}^6\)、\(\dot{q}^8\)・・・でもいいんじゃない？

ってなります(笑)

正直、この辺はわかりません。

ここの上手い説明を思いついたら紹介したいです・・・

今のところフワッとしたままですが、ラグランジアン\(L\)は\(L(\dot{q}^2)\)と思って、先に進んだ方が賢明かもしれません(笑)

まとめ

ガリレイの相対性原理について説明致しました～(^^)/

「ランダウ＝リフシッツの”力学”」をお持ちである方はお気づきだろうと思いますが、本記事の説明は「P.5とP.6の数行」の説明です(笑)

たった1ページしか進んでおりません！！！！(笑)

ごちゃごちゃランダウさんが説明しているので、ちゃんと説明したらこんなに長い記事になってしまったのです。

これゆえ、「いきなりランダウ=リフシッツの”力学”読んだら物理で絶望する説（第1報）」の結論になるのです(´・ω・`)

圧倒的に色々なバックグラウンドがない読めません！！

要所要所でわけがわからないことをランダウさんが語っておられますのでね(笑)

やはり難易度の高い文献は、1ページ30分かけて読むことはよくあるということです。

さらっと読むのは、それは「読んだだけ！！」ってことになりかねませんので、

僕はゆーーーーっくり読んでおります(笑)

※もう少ししたら、「正準方程式」まですっ飛びます！！

次回

次回は、
ランダウ＝リフシッツの”力学”P.7の

「§4.自由な質点のラグランジアン」

でも読んでみたいと思います(^^)/

ラグランジアン\(L=\sum_{a}\frac{m_{a}v_{a}^2}{2}\)という形が出てきていますね。

なんか、漠然としていたラグランジアン\(L\)が具体的な形で出てきています♪

参考図書

いくつかおすすめの解析力学の参考書を挙げておきます。

ランダウ力学

力学 (増訂第3版) ランダウ=リフシッツ理論物理学教程

エリ・ランダウ, イェ・エム・リフシッツ

3,860円(04/27 14:44時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

下記のような小教程もあります。

 

力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)

L.D.ランダウ, E.M.リフシッツ

1,650円(04/27 18:21時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

 

解析力学：マセマキャンパスゼミ

 

解析力学キャンパス・ゼミ 改訂3

馬場 敬之

4,480円(04/27 18:21時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。

解析力学ⅠⅡ：朝倉物理学大系

 

解析力学1 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,160円(04/27 18:21時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

解析力学2 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,380円(04/27 16:08時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。

詳解 力学演習

詳解力学演習

2,750円(04/27 13:41時点)

Amazon楽天市場Yahoo

Amazonの情報を掲載しています

こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。

ツイート