こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事は前回の続きとなります。
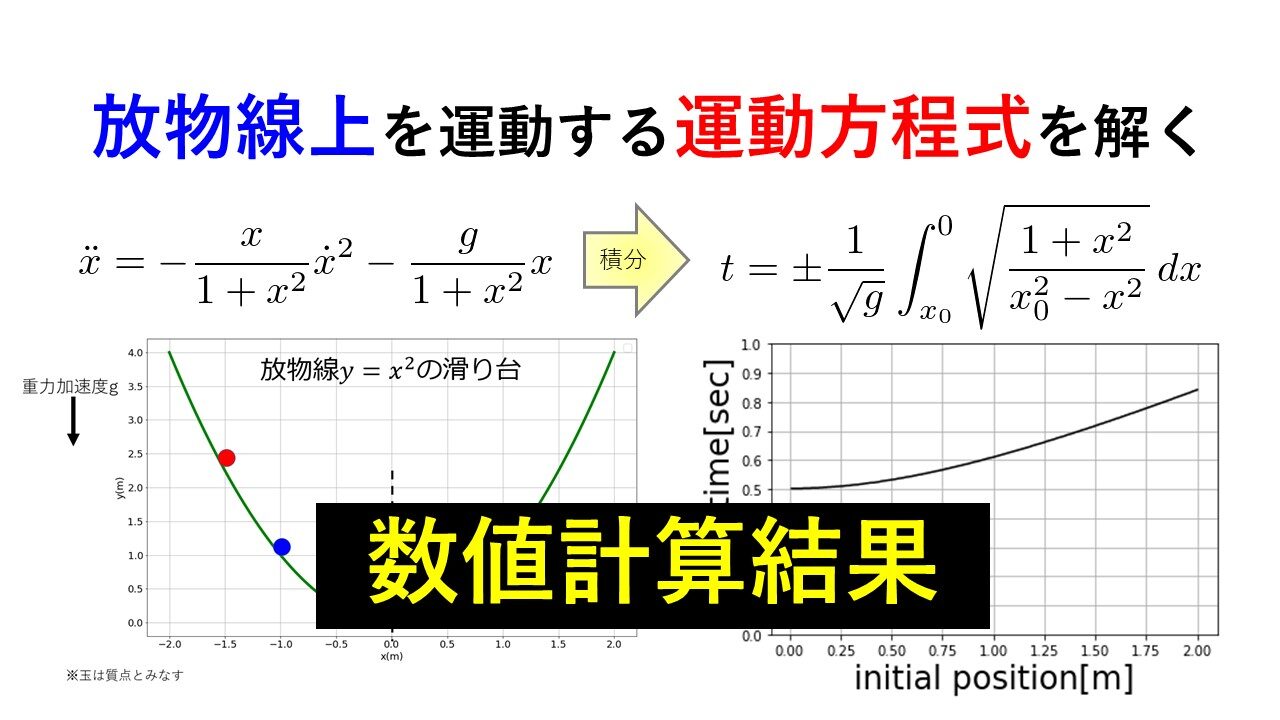
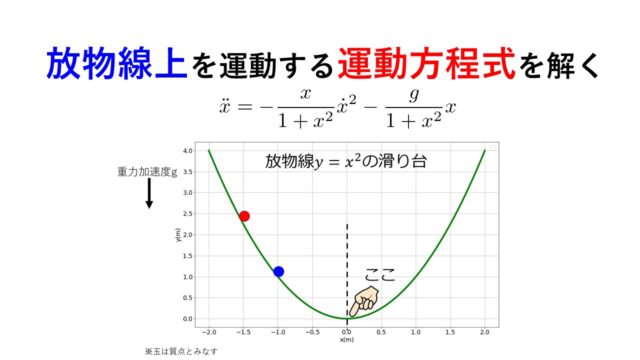
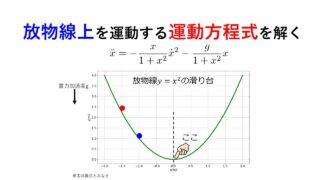
前回は以下のお題を出し、放物線上を運動する球の運動方程式を導出しました。
内容をさらっと振り返っておきましょう。
2つの球を初期の高さを変えて同時に静かに離すと、どちらが先に最下端に到達するか?
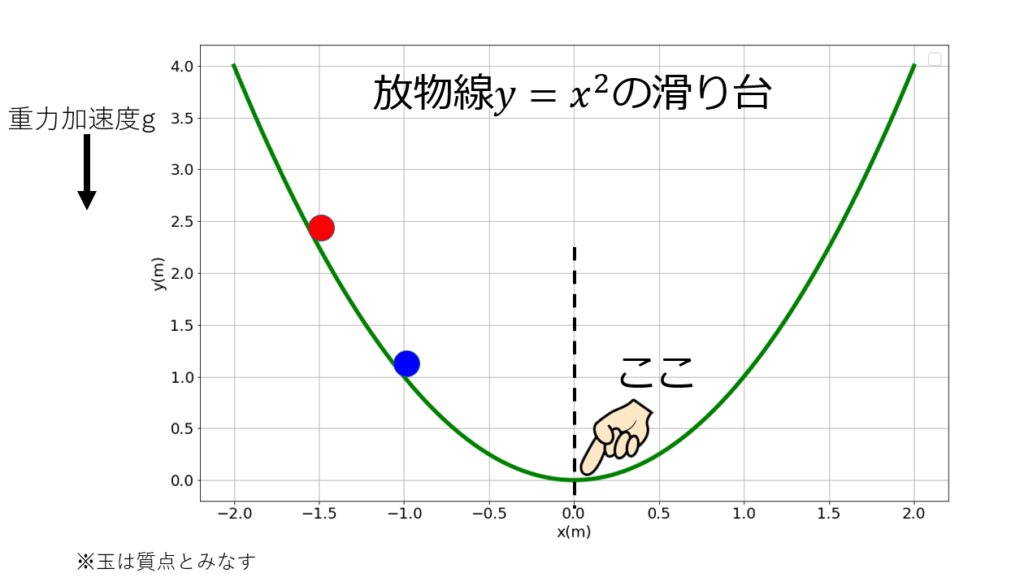
- 球は質点とみなす
- 空気抵抗は考えない
- 摩擦もなし
- 放物線$y=\frac{1}{2}x^2$上を運動
運動方程式は以下となりました。
\ddot{x}=-\frac{x}{1+x^2}\dot{x}^2-\frac{g}{1+x^2}x\tag{1}\end{align*}
これを$[x_{0},x]$まで積分すると、
t=\pm\frac{1}{\sqrt{g}}\int^{x}_{x_{0}} \sqrt{\frac{1+x^2}{x_{0}^2-x^2}}\, dx\tag{2}
\end{align*}
右辺の積分の結果は第2種楕円関数$E(x|k^2)$を使うことで以下
t=\pm\frac{1}{\sqrt{g}}E\bigg(\sin^{-1}\big(\frac{x}{x_{0}}\big)|-x_{0}^2\bigg)\tag{3}
\end{align*}
前回のおさらいはここまでです。
本記事では数値計算を使って放物線上に束縛された質点の運動方程式を数値計算で解きます。
- (1)の運動方程式を数値計算で解く
- (2)の運動方程式の解を積分して数値的に解く
数値計算のプログラミング言語はPythonを用います。
当ブログではPythonの基礎文法や数値解析の記事をそろえていますので参考にしてください。
(1)の運動方程式を数値計算で解く
放物線上を運動する質点の運動方程式がわかっているので、数値計算で求めてやれば解の振る舞いを知ることができますね。
運動方程式をおさらいしておきます。
\ddot{x}=-\frac{x}{1+x^2}\dot{x}^2-\frac{g}{1+x^2}x\tag{1}\end{align*}
積分は4次のルンゲクッタを使います。
初期位置$x_{0}=1.0[m]$テスト計算
試しに初期位置$x_{0}=1.0[m]$として計算してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
import numpy as np import matplotlib.pyplot as plt """ 4次のルンゲ-クッタ法による1次元ニュートン方程式の解法 The fourth-order Runge-Kutta method for the 1D Newton's equation # 例: 放物線上を運動する球 (harmonic oscilation) """ ########################## ##### パラメータ設定 ##### ########################## g = 9.81 t0 = 0.0 t1 = 20 N = 1000 del_t = (t1-t0)/N # time grid ########################## ##### 初期状態設定 ##### ########################## # initial condition x0 = 1.0 v0 = 0.0 x, v = x0, v0 ########################## ##### 運動方程式 ##### ########################## def f(x, v, t): return -x/(x**2+1)*v**2-g/(x**2 +1)*x tpoints = np.arange(t0, t1, del_t) xpoints = [] vpoints = [] ########################## ##### 4次ルンゲクッタ ##### ########################## for t in tpoints: xpoints.append(x) vpoints.append(v) k1v =f(x, v, t)*del_t k1x = v * del_t k2v = f(x+k1x/2, v+k1v/2, t+del_t/2 )*del_t k2x =(v+k1v/2)*del_t k3v =f (x+k2x/2, v+k2v/2, t+del_t/2 )*del_t k3x =(v+k2v/2 ) *del_t k4v = f(x+k3x, v+k3v, t+del_t )*del_t k4x = (v+k3v )*del_t v += (k1v + 2 * k2v + 2* k3v + k4v)/6 x += (k1x + 2 * k2x + 2* k3x + k4x)/6 ########################## ##### グラフ化 ##### ########################## plt.plot (tpoints, xpoints, label='4th order Runge-Kutta', color='black') plt.xlabel("t", fontsize=24) plt.ylabel("x(t)", fontsize=24) plt.grid() |
【結果】
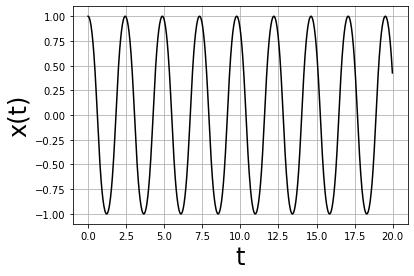
$x$方向を行ったり来たりしている結果ですね。
放物線上を運動するので正しい結果に見えます。
初期位置から最下端の時刻の関係
では、今度は初期位置と最下端の時刻の関係をグラフ化します。
最下端までにかかる時間なので積分区間は$[x_{0},0]$までとなります。
t_{bottom}=\pm\frac{1}{\sqrt{g}}\int^{0}_{x_{0}} \sqrt{\frac{1+x^2}{x_{0}^2-x^2}}\, dx\tag{2}
\end{align*}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
import numpy as np import matplotlib.pyplot as plt """ 4次のルンゲ-クッタ法による1次元ニュートン方程式の解法 The fourth-order Runge-Kutta method for the 1D Newton's equation # 例: 放物線上を運動する球 (harmonic oscilation) """ ########################## ##### パラメータ設定 ##### ########################## g = 9.81 t0 = 0.0 t1 = 10 N = 10000 del_t = (t1-t0)/N # time grid ########################## ##### 初期状態設定 ##### ########################## # initial condition x0_list = np.arange(0.01,2.01,0.01) v0 = 0.0 ########################## ##### 運動方程式 ##### ########################## def f(x, v, t): return -x/(x**2+1)*v**2-g/(x**2 +1)*x ########################## ##### 4次ルンゲクッタ ##### ########################## def RK4(x0): x, v = x0, v0 tpoints = np.arange(t0, t1, del_t) xpoints = [] vpoints = [] for t in tpoints: xpoints.append(x) vpoints.append(v) k1v =f(x, v, t)*del_t k1x = v * del_t k2v = f(x+k1x/2, v+k1v/2, t+del_t/2 )*del_t k2x =(v+k1v/2)*del_t k3v =f (x+k2x/2, v+k2v/2, t+del_t/2 )*del_t k3x =(v+k2v/2 ) *del_t k4v = f(x+k3x, v+k3v, t+del_t )*del_t k4x = (v+k3v )*del_t v += (k1v + 2 * k2v + 2* k3v + k4v)/6 x += (k1x + 2 * k2x + 2* k3x + k4x)/6 # numpyに変換 xpoints_np = np.array(xpoints) tpoints_np = np.array(tpoints) return tpoints_np[np.where(xpoints_np<0)[0][0]] # 最下点に来た時刻のリスト height0_time_list = [] # 初期位置から最下点に来た時刻を計算 for x0 in x0_list: height0_time_list.append( RK4(x0)) ########################## ##### グラフ化 ##### ########################## plt.plot (x0_list, height0_time_list, label='4th order Runge-Kutta', color='black') plt.xlabel("initial position[m]", fontsize=24) plt.ylabel("Arrival time[sec]", fontsize=24) plt.grid() plt.yticks(np.arange(0,1.1,0.1)) |
30秒くらい時間がかかります。
【結果】
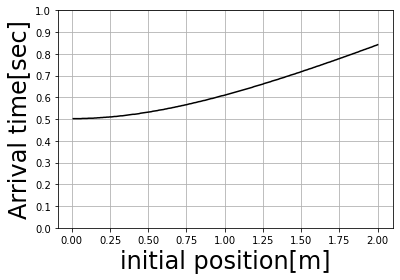
距離を見ると青球と赤球で最下端に来る時間には0.3秒くらいの差しかないことがわかります。
名古屋市科学館で実験すると確かに初期高さが低い球の方が早く下に到達しました。
実際の球は大きさがある球体のため回転の運動方程式も考える必要がありますが、今回の数値計算は質点としてモデル化して考えました。
?
どうなの(・・? pic.twitter.com/tSR1lEr3BM— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) October 18, 2021
(2)の運動方程式の解を積分して数値的に解く
\ddot{x}=-\frac{x}{1+x^2}\dot{x}^2-\frac{g}{1+x^2}x\tag{1}\end{align*}
これを初期位置から最下端までの位置$[x_{0},0]$で積分すると、
t_{bottom}=\pm\frac{1}{\sqrt{g}}\int^{0}_{x_{0}} \sqrt{\frac{1+x^2}{x_{0}^2-x^2}}\, dx\tag{2}
\end{align*}
間違いがなければ一致するはずですね。
(2)の積分にはscipyのライブラリを使用しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import numpy as np import matplotlib.pyplot from scipy import integrate g = 9.81 x = np.arange(0.01, 2.01, 0.01) t = np.arange(0.01, 2.01, 0.01) x0_list = np.arange(0.01,2.01,0.01) # initial state x0 = 1.0 f1 = np.arcsin(x/x0 ) # 理論計算 height0_time_theory = np.array([( 1/(g**0.5)) * integrate.quad(lambda x: np.sqrt((1+x**2)/(x0**2-x**2)), 0, x0)[0] for x0 in x0_list]) ########################## ##### グラフ化 ##### ########################## plt.plot (x0_list, height0_time_list, label='(1)4th order Runge-Kutta', color='black', linewidth=3) plt.plot (x0_list, height0_time_theory, label='(2)theory_integrate', color='red') plt.xlabel("initial position[m]", fontsize=24) plt.ylabel("Arrival time[sec]", fontsize=24) plt.grid() plt.yticks(np.arange(0,1.1,0.1)) plt.legend() |
【結果】
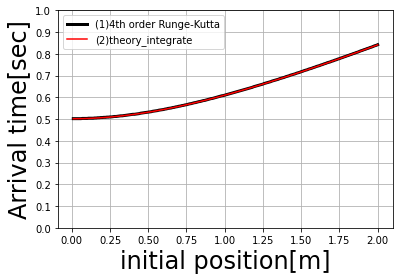
- 赤線:(1)の運動方程式の数値計算
- 黒線:(2)の運動方程式の解を積分した数値計算
重なっているので(2)の積分は間違っていなさそうです。
まとめ
放物線上を運動する質点の運動方程式の振る舞いを数値計算で確認しました。
今回解いた方程式はこちらです。
\ddot{x}=-\frac{x}{1+x^2}\dot{x}^2-\frac{g}{1+x^2}x\tag{1}\end{align*}
これを初期位置から最下端までの位置$[x_{0},0]$で積分すると、
t_{bottom}=\pm\frac{1}{\sqrt{g}}\int^{0}_{x_{0}} \sqrt{\frac{1+x^2}{x_{0}^2-x^2}}\, dx\tag{2}
\end{align*}
(2)をもう少し頑張って積分した結果が以下となることがわかっています。
t=\pm\frac{1}{\sqrt{g}}\sqrt{x_{0}^2-x^2}E\bigg(\sin^{-1}\big(\frac{x}{x_{0}}\big)|-x_{0}^2\bigg)\tag{3}
\end{align*}
右辺の積分の結果は第2種楕円関数$E(x|k^2)$を使えばよく、追々頑張って導出したいと思います(‘ω’)ノ