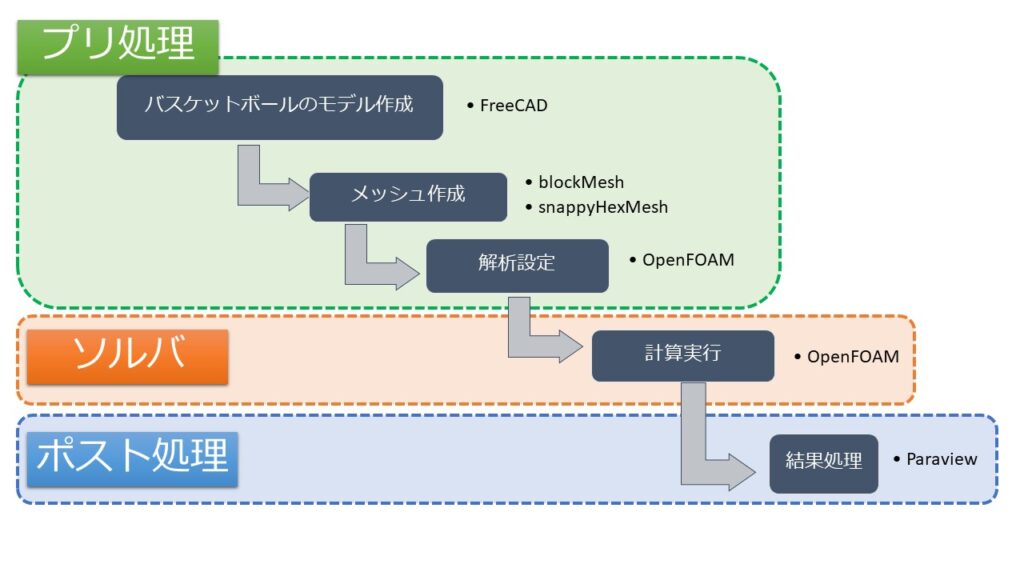
こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
本記事ではOpenFOAMのバスケットボールまわりの流体解析を行う下準備のための記事です。
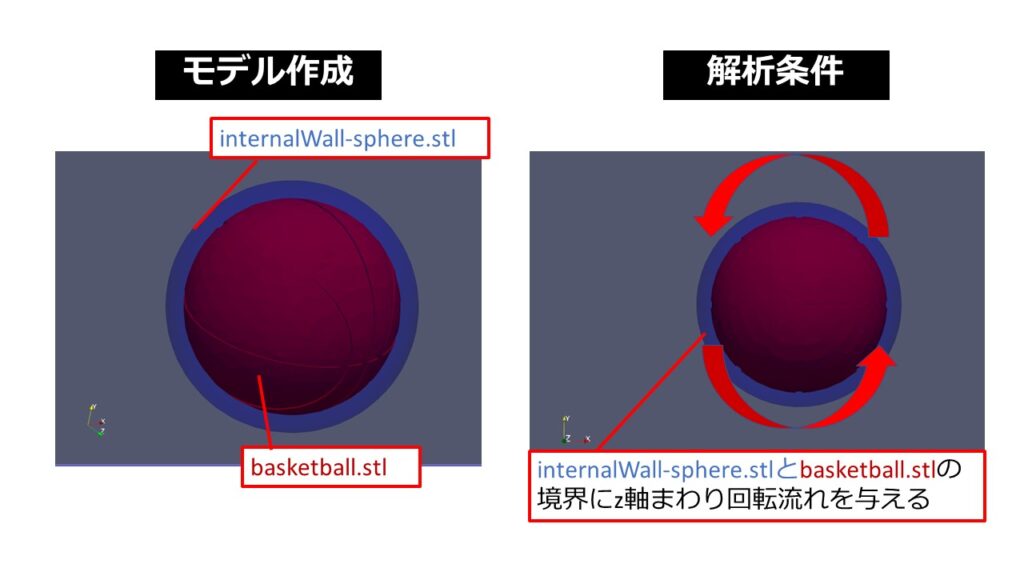
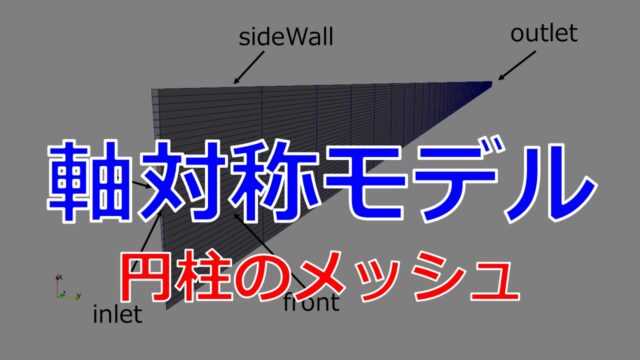
球体まわりのメッシュをinnerとouterに分けて別々で6面体メッシュで生成しました。
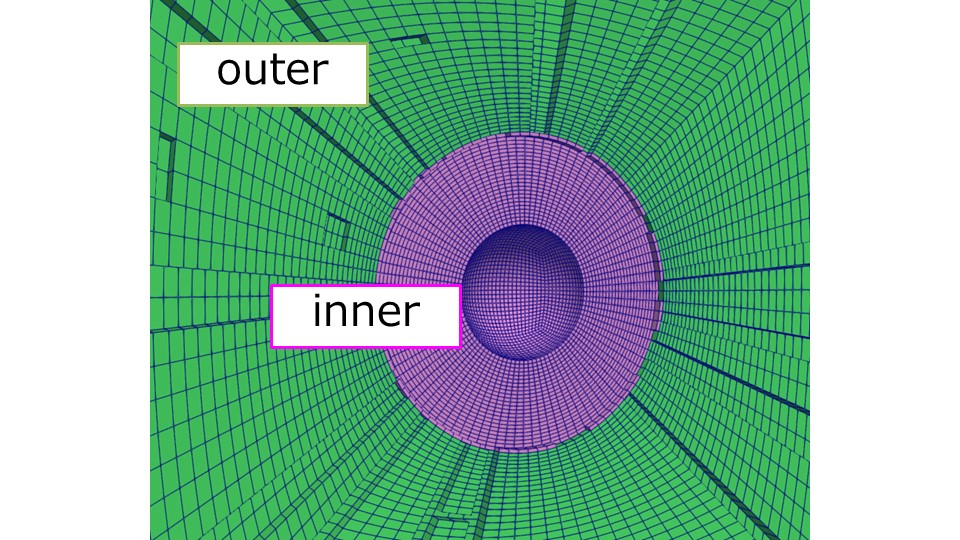
innerとouterをcyclicAMI周期境界でつないで球体まわりの解析を行う
本記事の内容は下記の参考記事のモデル作成です。
【OpenFOAM】ゴルフボールはどう打ったら最もよく飛ぶのか
※モデルを頂きブログ記事での解説のお許しを得たので皆さんに共有いたします。
記事内で「SALOMEを用いて下図のようなメッシュを作成しました。全てヘキサで作成した後にrefineMeshにて一部をポリヘドラに細分化」と書いてありますが、当ブログではゴルフボールではなくバスケットボールまわりのメッシュ作成をします。また、全てblockMeshのみで作成するので記事内の作り方と異なります。
1度試しにsnappyHexMeshでメッシュ生成しましたが、バスケットボールの凹みの部分のメッシュを細かくしないといけなく計算時間がかかるので本記事の内容の通りメッシュを作成しなおすことにしました。
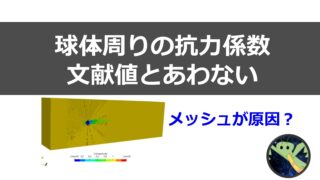
以前した球体でしたときの効力係数0.4より約4倍大きい。
メッシュがだめだな。 https://t.co/gcOkMWjD7j— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) September 2, 2022
バスケットボールはシュートの際に1秒間に2回転ほどしているそうです。
味方にパスをするときはもっと高速で回転していると思いますが、果たして回転させるとどう違うのか考察をしていく心意気です(^^)
モデル作成と勉強しながら、アウトプットのため記事にまとめていきます。最終的にはOpenFOAMを使ってバスケットボールまわりの流れを解析します。
頑張りますよ(‘ω’)ノ
使用環境
- Windows11
- FreeCAD：0.20
- OpenFOAM-v2212 (2006)ESI版
- Paraview：5.11.0
innerとouterを合体させる
別のモデルのメッシュ情報を合体させるためにはmergeMeshesを使います。
まず、現在のフォルダの状態を確認しておきましょう。
|
1 2 |
ls inner outer |
モデル情報は2つあります。
- バスケットボール周辺：inner
- 外部の計算領域：outer
こちらはParaViewで別々モデルを表示させただけですので、メッシュ情報としてはまだ合体していません。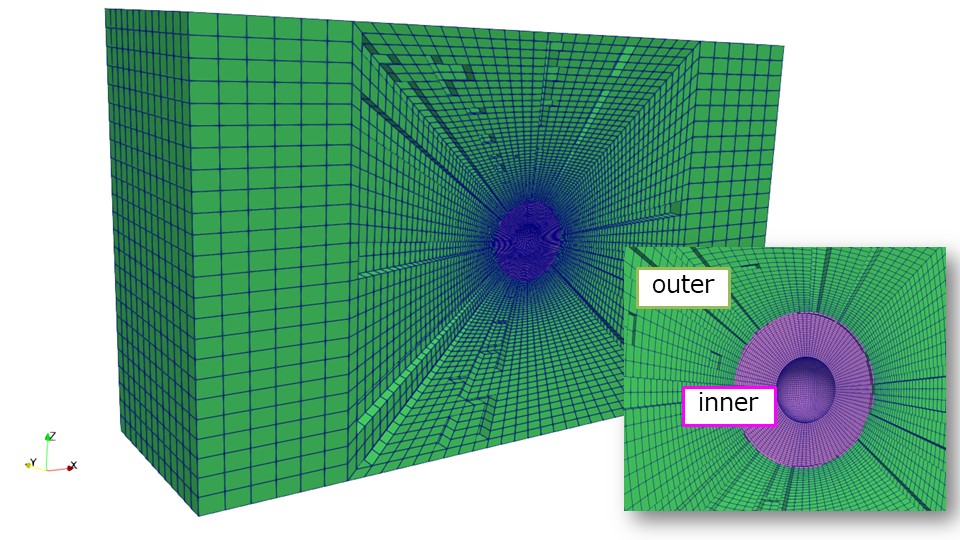
まずはinnerモデルをコピーします。
|
1 |
cp -r inner merge |
これで新たなmergeというモデルができたので、そちらにinnerとouterを合体させたモデルを作成します。
|
1 2 |
ls inner merge outer |
合体するには以下のコマンドを使います。
|
1 |
mergeMeshes -overwrite merge outer |
これによりmerge（元はinnerのモデル）にouterのメッシュが追加されました。
では、mergeでのメッシュ状態をParaViewで確認してみましょう。
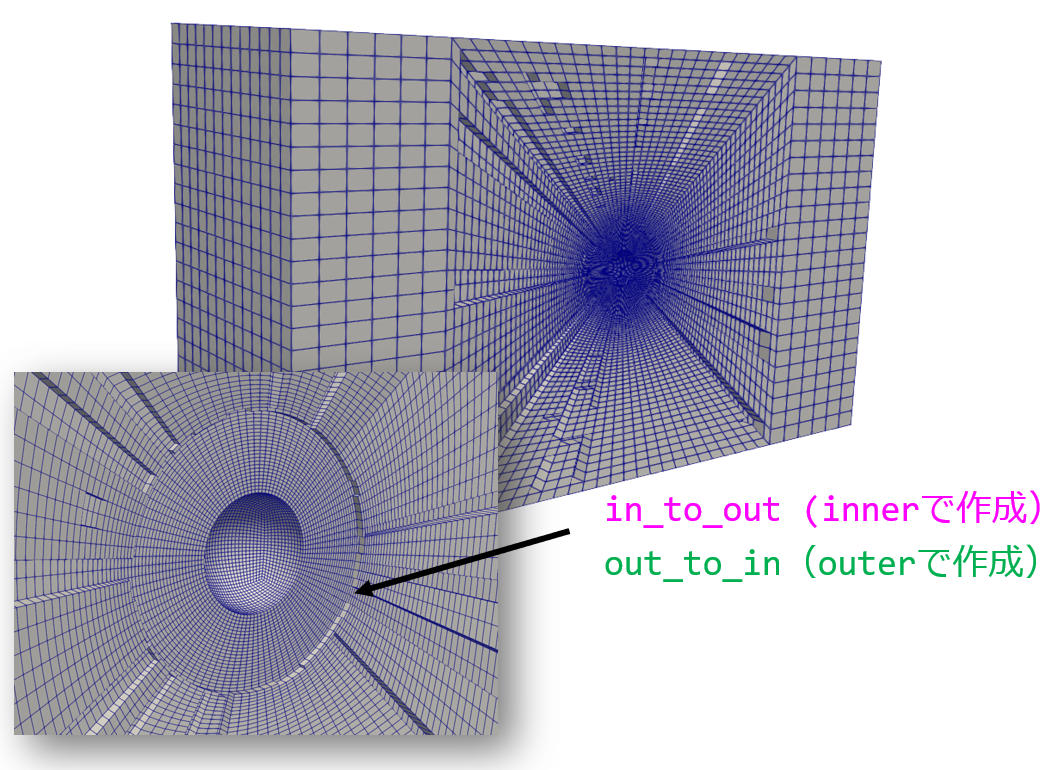
この状態ではin_to_outとout_to_inの境界の節点は結合しておらず別々の境界となっています。この状態で解析をすると球体の空洞のまわりというよりin_to_out（もしくはout_to_in）が壁になってしまう解析になります。
cyclicAMI
異なるメッシュ状態であっても周期境界 (格子の切り方が違う2面をつなぐ Cyclic Arbitrary Mesh Interface (cyclicAMI)タイプ)を課すことで解析することができます。
cyclicAMIの記事は下記にも書きましたのでご参考ください。
先ほど作成したmergeでの状態をコピーします。
|
1 |
cp -r merge cyclicAMI_run |
解析設定はcyclicAMI_runで行うことにします。
やることは以下の2つです。
- constant/polyMesh/boundaryの境界条件を変更
- 境界条件0/U,p,k,omega,nut,alphatの境界条件を変更
constant/polyMesh/boundary（修正前）
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
6 ( in_to_out { type wall; inGroups 1(wall); nFaces 3456; startFace 759744; } ball { type wall; inGroups 1(wall); nFaces 3456; startFace 763200; } out_wall { type patch; nFaces 3456; startFace 766656; } out_to_in { type wall; inGroups 1(wall); nFaces 3456; startFace 770112; } inlet { type wall; inGroups 1(wall); nFaces 576; startFace 773568; } outlet { type wall; inGroups 1(wall); nFaces 576; startFace 774144; } ) |
0/U（修正前）
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
dimensions [0 1 -1 0 0 0 0]; internalField uniform (1.0 0.0 0.0); boundaryField { ball { type fixedValue; value uniform (0 0 0); } inlet { type fixedValue; value uniform (1 0 0); } outlet { type zeroGradient; } out_wall { type slip; } } |
これをchangeDictionaryDictで修正します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
boundary { in_to_out { type cyclicAMI; machTolerance 1e-6; neighbourPatch out_to_in; transform noOrdering; } out_to_in { type cyclicAMI; machTolerance 1e-6; neighbourPatch in_to_out; transform noOrdering; } } U { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } p { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } k { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } omega { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } nuTilda { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } nut { boundaryField { in_to_out { type cyclicAMI; neighbourPatch out_to_in; } out_to_in { type cyclicAMI; neighbourPatch in_to_out; } } } |
もう少し楽な書き方があるかもしれませんが・・・
|
1 |
changeDictionary |
これで「constant/polyMesh/boundary」と「0/U, 0/p, 0/k, 0/omega, 0/nuTilda, 0/nut」の境界条件が変更されます。
これにより境界条件が変わります。
解析実行
では解析実行しましょう。
今回は非圧縮の定常流れ（k-omega SST）使います。
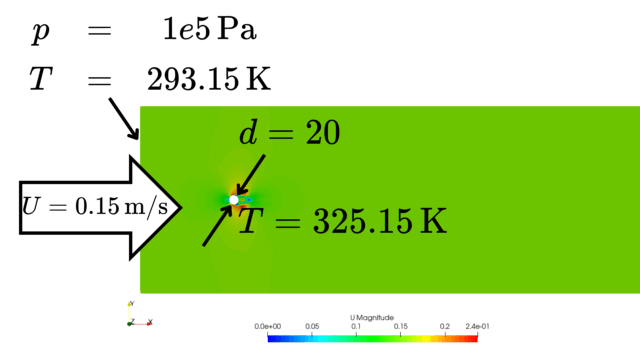
- inlet：流速(1.0, 0, 0) m/s
- 動粘性係数:nu 1.5e-5[m2/s]
system/controlDictには残差、連続の式の誤差、抗力係数を出力する設定を記述します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
application simpleFoam; startFrom startTime; startTime 0; stopAt endTime; endTime 1000; deltaT 1.0; adjustTimeStep no; maxCo 0.9; writeControl timeStep; writeInterval 50; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable yes; functions { forceCoeffs(sphereMeshed) { type forceCoeffs; libs ("libforces.so"); writeControl timeStep; timeInterval 1; log no; patches (ball); rho rhoInf; rhoInf 1; liftDir (0 1 0); dragDir (1 0 0); CofR (0 0 0); pitchAxis (0 0 1); magUInf 1.0; lRef 0.25; Aref 0.05144576; //r_out = 0.128 (radius 128mm) } continuityError1 { type continuityError; libs ( fieldFunctionObjects ); // Mandatory entries (unmodifiable)// Optional entries (runtime modifiable) phi phi; // Optional (inherited) entries writePrecision 8; writeToFile yes; useUserTime yes; region region0; enabled yes; log yes; timeStart 0; timeEnd 6000; executeControl timeStep; executeInterval 1; writeControl timeStep; writeInterval 50; } residuals { type solverInfo; libs ("libutilityFunctionObjects.so"); fields (U p k omega); } //#includeFunc residuals(U,p,k,epsilon); #includeFunc yPlus; #includeFunc CourantNo; } |
今回は半径は128ｍｍ（バスケットボールが125mm）なので投影面積$A=\pi r^2$より計算される値「Aref 0.05144576;」を書きました。
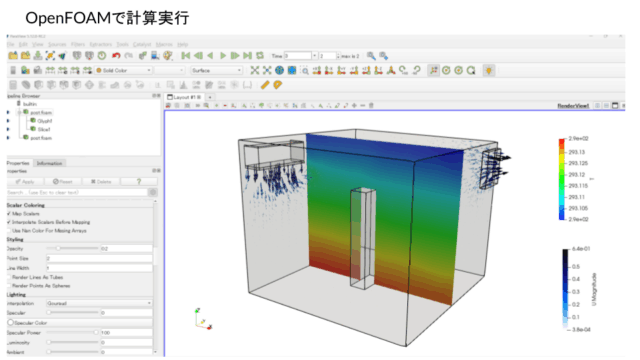
では、計算実行します。
|
1 |
simpleFoam |
計算結果を確認します。
残差と連続の式による誤差は最低確認するようにしましょう。
連続の式の誤差
- sum local : 誤差絶対値の格子体積重み付け平均
- global : 誤差(符号あり)の格子体積重み付け平均
- cumulative : globalの累積
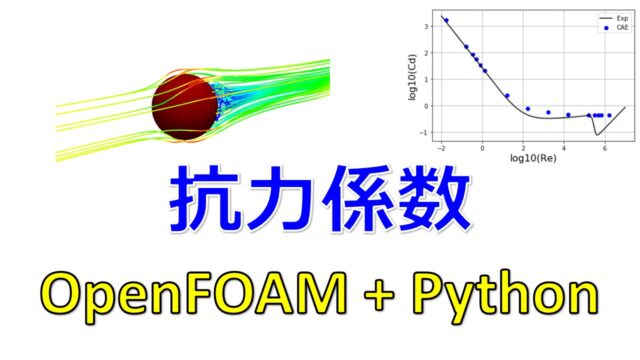
レイノルズ数：$Re=\frac{Ud}{\nu}=\frac{1.0*0.128}{1.5e-5}=8,533$なので乱流状態です。
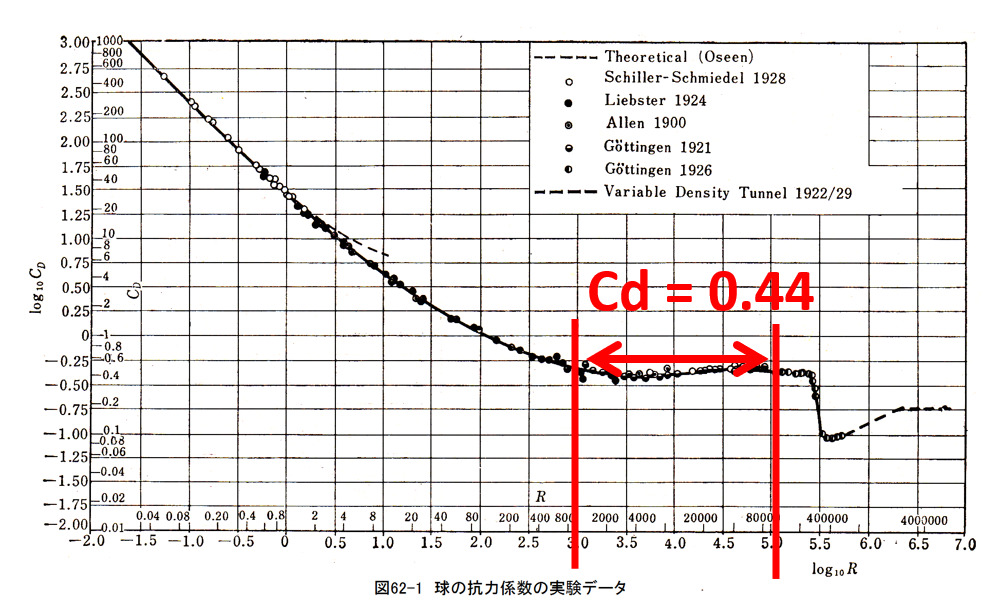
乱流状態だと抗力係数は一定値0.44になるということです。
高いレイノルズ数になるとドラッグクライシスと呼ばれる抗力係数がガクっと下がる領域が出ますが、この領域をCAE解析で再現するには相当なメッシュ数と非定常流れを解かないといけないため、本記事では扱いません（自宅PCのすぺっくではきついです）。
今回計算したモデルで抗力係数を確認してみましょう。
postProcessing/forceCoeffs(sphereMeshed)/0/coefficient.dat
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# Force and moment coefficients # dragDir : (1.000000e+00 0.000000e+00 0.000000e+00) # sideDir : (0.000000e+00 0.000000e+00 -1.000000e+00) # liftDir : (0.000000e+00 1.000000e+00 0.000000e+00) # rollAxis : (1.000000e+00 0.000000e+00 0.000000e+00) # pitchAxis : (0.000000e+00 0.000000e+00 -1.000000e+00) # yawAxis : (0.000000e+00 1.000000e+00 0.000000e+00) # magUInf : 1.000000e+00 # lRef : 2.500000e-01 # Aref : 5.144576e-02 # CofR : (0.000000e+00 0.000000e+00 0.000000e+00) # # Time Cd Cd(f) Cd(r) Cl Cl(f) Cl(r) CmPitch CmRoll CmYaw Cs Cs(f) Cs(r) 1 3.561872e+00 1.780936e+00 1.780936e+00 -9.377739e-05 -4.722456e-05 -4.655283e-05 -3.358673e-07 -4.820535e-10 8.039906e-08 -1.124611e-04 -5.615015e-05 -5.631094e-05 2 2.126920e+00 1.063460e+00 1.063460e+00 2.363863e-02 1.116326e-02 1.247537e-02 -6.560583e-04 3.151787e-09 2.900004e-04 1.721941e-02 8.899706e-03 8.319705e-03 （省略） 498 2.306942e-01 1.153425e-01 1.153517e-01 -2.090815e-02 -1.060853e-02 -1.029963e-02 -1.544501e-04 -4.631907e-06 3.042265e-04 -3.263374e-02 -1.601264e-02 -1.662110e-02 499 2.297875e-01 1.148890e-01 1.148986e-01 -1.939405e-02 -9.858904e-03 -9.535143e-03 -1.618804e-04 -4.795832e-06 3.255164e-04 -2.708027e-02 -1.321462e-02 -1.386565e-02 500 2.288799e-01 1.144350e-01 1.144448e-01 -1.847565e-02 -9.405861e-03 -9.069789e-03 -1.680358e-04 -4.894851e-06 3.423224e-04 -2.304837e-02 -1.118186e-02 -1.186651e-02 3 |
800~1000stepの平均の抗力係数Cd値は0.25です。
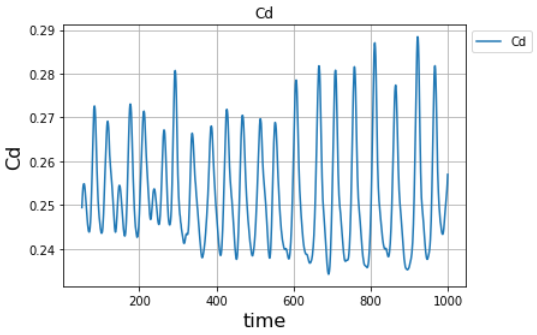
これは球体まわりの抗力係数Cd=0.44と比べると小さい値です。
文献値とCAEの結果が合わなかった原因はまだわかりませんが、以下の要因が考えられます。
- 解析領域の狭さ
- スキームの選択
- 球体周りのメッシュの直交性の悪さ
- cyclicAMIが悪さをしている
- その他計算条件の見直し（乱流モデルなど）
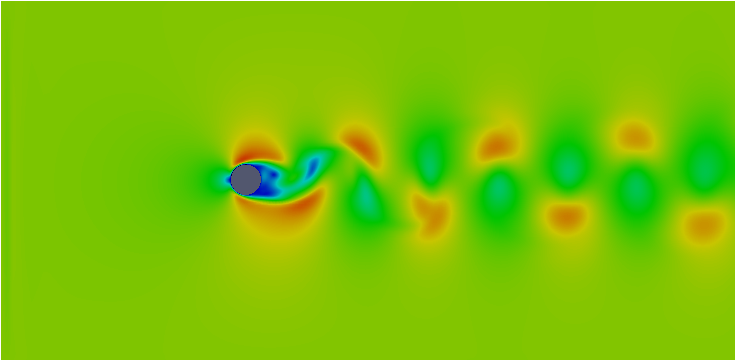
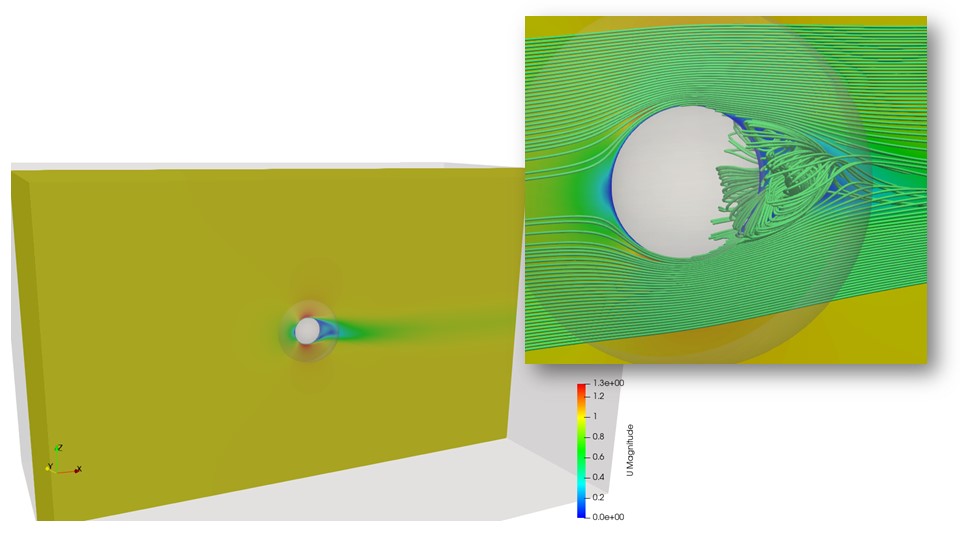
球体周りで渦が発生しています。
球体周り流れの再現性など影響を受けると考えれれる原因をひとつずつ潰していくしかないですね。
改善の余地はまだありそうなので、次の機会にトライしてみます。
まとめ
今回はバスケットボールのまわりの下準備のため球体まわりの流体解析を行いました。
メッシュ生成は前回までの記事でblockMeshで作成し全てのメッシュを6面体メッシュで作りました。
今回行った球体まわりの抗力係数は文献値のCd=0.44になりませんでした。本記事のように抗力係数が正しい値にならなかった場合には解析条件を修正する必要があります。
例えば以下の記事では概ね文献値通りの抗力係数を示してくれます。
こちらと比較して今回の解析条件は何が違うのか調査する必要があります。
次回のアクションとしては、以下の修正を行ったときの結果への影響を検証します。
- 解析領域を広げる
- cyclicAMIをやめる
- 球体周りのメッシュサイズを細かくする
結論「球体周りのメッシュサイズを細かくする」ことで文献値と近くなりました。
おすすめ参考図書
☟こちらは、OpenFOAMの日本語書籍として重宝しているわかりやすい参考書だと思います。
☟こちらもOpenFOMの古いバージョンでの和訳になります。さすがにこちらはバージョンに対する日本語でのケアはしていないので、OpenFOAMに慣れている方は購入しても良いかと思います。僕は「日本語でまとまっている内容」なので少し重宝しています。
☟以下に、もっと初心者向けの同人誌を紹介しておきます。
初心者は「ってか、まずどうやってOpenFOAMをインストールするの？」というところからつまずきがちです。
そんな時は、以下の書籍をおすすめします。
改訂新版 OpenFOAMの歩き方 (技術の泉シリーズ（NextPublishing）)
インストール方法とチュートリアルで流体解析を体験・・・ちょっと高度な解析まで解説があります。著者曰くOpenFOAMのバージョンの追跡を行いながら、書籍をアップデートするようなので安心ですね。
OpenFOAMコードの辞書的な扱いとしては以下の参考書が大変役に立ちます。
本記事ではESI版のOpenFOAMを使っているため本書のFoundation版で対応していない部分がありますが、その辺を考慮しても持っていて損はないでしょう。
今回の記事はこちらの著者の方からモデル提供をいただきモデル作成の解説を行いました。
OpenFOAMでメッシュ作成
Follow @t_kun_kamakiri
