【OpenFOAM】領域ごとに対流項スキームを変えるzoneBlended schemeを試してみた

計算シミュレーションにおける数値安定性の向上は、常に重要な課題となっています。特に対流項をどのように離散化して数値計算を行うかは、解の精度と安定性に影響します。

今回、OpenFOAM v2412で各領域ごとに対流項スキームを柔軟に切り替えるzoneBlended scheme機能が追加されていたので試みました。

本記事の内容

移流方程式$\frac{\partial T(x,t)}{\partial t}+u\frac{\partial T(x,t)}{\partial x}=0$において領域をごとに対流項スキームを変えるブレンドスキームを紹介する

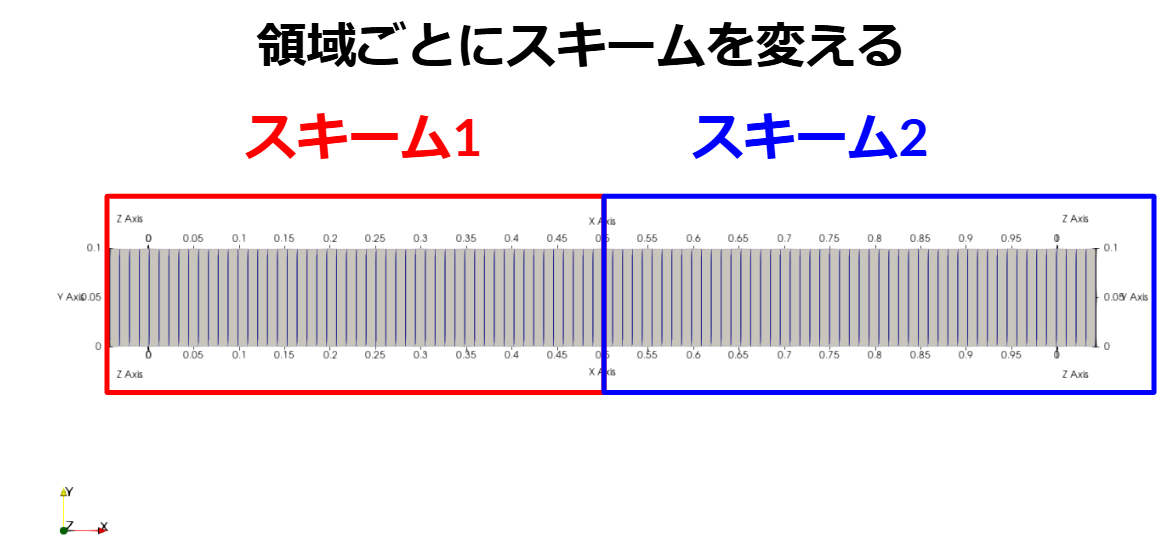
本記事では、以下のように領域ごとに対流項スキームを変えることにします。

あわせて読みたい

対流項の発散スキームの比較
こちらはOpenFOAMの離散化スキームの比較として一番参考になる記事でしょう。
Divergence scheme example
公式サイトにも離散化スキームに対する検討がされています。メッシュと離散化スキームの選択次第で結果がずいぶんと変わるのがわかるでしょう。
OpenFOAM6.2 Numerical schemes
OpenFOAM Basic Training
第1回オープンCAE講習会 OpenFOAM初中級講習B
upwind_difference.pdf (xrea.com)
こちらのpdfはスキームについてよくまとめられています。

OpenFOAM v2412 Ubuntu-22.04(WSL2)

対流項スキームでの結果の違い
1. OpenFOAMで実行
OpenFOAMでスキームの設定
まとめ
計算力学技術者のための問題アプリ
OpenFOAMに関する技術書を販売中！
お勧めの参考書

対流項スキームでの結果の違い

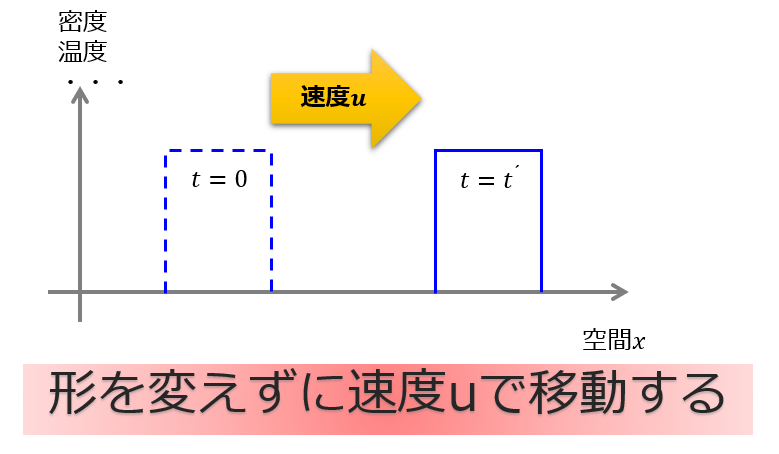
移流方程式は以下のような式にしたがう方程式のことを指します。

１次元の移流方程式

\begin{align*}\frac{\partial T(x,t)}{\partial t}+u\frac{\partial T(x,t)}{\partial x}=0\tag{1}\end{align*}

※$u$：一定速度

1次元の移流方程式は、下記の絵のように何かの物理量を形を変えずに一定速度$u$で運ぶ方程式を意味しています。

横軸は空間$x$ですが、縦軸は「密度」や「温度」だったり色々考えることができます。本記事では、温度$T$として扱うことにします。

OpenFOAMで実行

ソルバはscalarTransportFoamを使用しています。

scalarTransportFoamは以下の偏微分方程式を解く非定常のソルバーです。

\begin{align*}
\frac{\partial T}{\partial t}+\nabla\cdot(\boldsymbol{u}T)-\nabla\cdot (D_{T}\nabla T)=\boldsymbol{S}_{T}\tag{1}
\end{align*}

あわせて読みたい

scalarTransportFoam

本記事では(1)を少し簡単にするために、

生成項を0：$\boldsymbol{S}_{T}=0$
拡散項を0：$D_{T}=0$
流速は一定：$\boldsymbol{u}=(0.1, 0, 0)$

あわせて読みたい

(1)の第二項をどのような離散スキームを選択するかによって以下の時間発展のように結果が異なります。
解がなまってしまうものや振動してしまうものがあります。

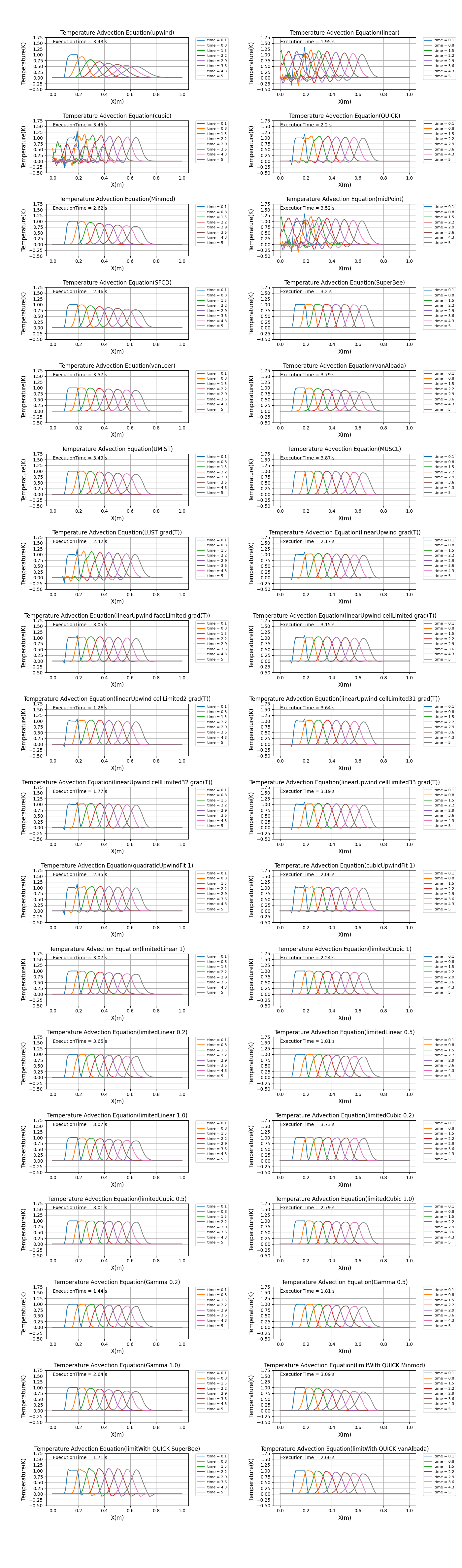
一般的には以下のように考えておいて良いでしょう。

1次精度は安定だが数値拡散（数値粘性）が生じやすい
高次精度は解をシャープにとらえられるが振動が生じやすく不安定になりやすい
TVDは解をシャープにとらえようとしつつ振動が生じないように工夫している

おおよそポイントはこれくらいでしょう。

OpenFOAMでスキームの設定

モデルはgithubにアップしています。

FaceZoneの追加

FaceZoneはsystem/topoSetDictで行います。

system/topoSetDict

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  v2412                                 |
|   \\  /    A nd           | Website:  www.openfoam.com                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    object      topoSetDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

actions
(
    {
        name    linearUpwindFaceSet;
        type    faceSet;
        action  new;
        source  boxToFace;
        box     (0 -100 -100)(0.5 100 100);
    }
    {
        name    linearUpwindCellSet;
        type    cellSet;
        action  new;
        source  boxToCell;
        box     (0 -100 -100)(0.3 100 100);
    }
    {
        name        linearUpwindFaceZone;
        type        faceZoneSet;
        action      new;
        source      setsToFaceZone;
        faceSet     linearUpwindFaceSet;
        cellSet     linearUpwindCellSet;
    }

    {
        name    upwindFaceSet;
        type    faceSet;
        action  new;
        source  boxToFace;
        box     (0.5 -100 -100)(100 100 100);
    }
    {
        name    upwindCellSet;
        type    cellSet;
        action  new;
        source  boxToCell;
        box     (0.3 -100 -100)(100 100 100);
    }
    {
        name    upwindFaceZoneSet;
        type    faceZoneSet;
        action  new;
        source  setsToFaceZone;
        faceSet upwindFaceSet;
        cellSet upwindCellSet;
    }
);


// ************************************************************************* //

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: v2412 |

| \\ / A nd | Website: www.openfoam.com |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class dictionary;

object topoSetDict;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

actions

(

{

name linearUpwindFaceSet;

type faceSet;

action new;

source boxToFace;

box (0 -100 -100)(0.5 100 100);

}

{

name linearUpwindCellSet;

type cellSet;

action new;

source boxToCell;

box (0 -100 -100)(0.3 100 100);

}

{

name linearUpwindFaceZone;

type faceZoneSet;

action new;

source setsToFaceZone;

faceSet linearUpwindFaceSet;

cellSet linearUpwindCellSet;

}

{

name upwindFaceSet;

type faceSet;

action new;

source boxToFace;

box (0.5 -100 -100)(100 100 100);

}

{

name upwindCellSet;

type cellSet;

action new;

source boxToCell;

box (0.3 -100 -100)(100 100 100);

}

{

name upwindFaceZoneSet;

type faceZoneSet;

action new;

source setsToFaceZone;

faceSet upwindFaceSet;

cellSet upwindCellSet;

}

);

// ************************************************************************* //

2つの領域を作成しています。

対流項スキームの変更

FaceZoneはsystem/fvSchemesで行います。
変更箇所だけをしまします。
詳しくはgithubをご確認ください。

system/fvSchemes

divSchemes
{
    // div(phi,T) Gauss upwind grad(T);
    div(phi,T) Gauss zoneBlended
    {
        default         upwind grad(T);
        linearUpwindFaceZone  linearUpwind grad(T);
        upwindFaceZoneSet  upwind;
    };
}

divSchemes

{

// div(phi,T) Gauss upwind grad(T);

div(phi,T) Gauss zoneBlended

{

default upwind grad(T);

linearUpwindFaceZone linearUpwind grad(T);

upwindFaceZoneSet upwind;

};

}

zoneBlendedを使って各領域のスキームは以下としています。

領域1のスキーム1：2次精度線形風上差分（linearUpwind ）
領域2のスキーム2：1次精度風上差分（upwind）

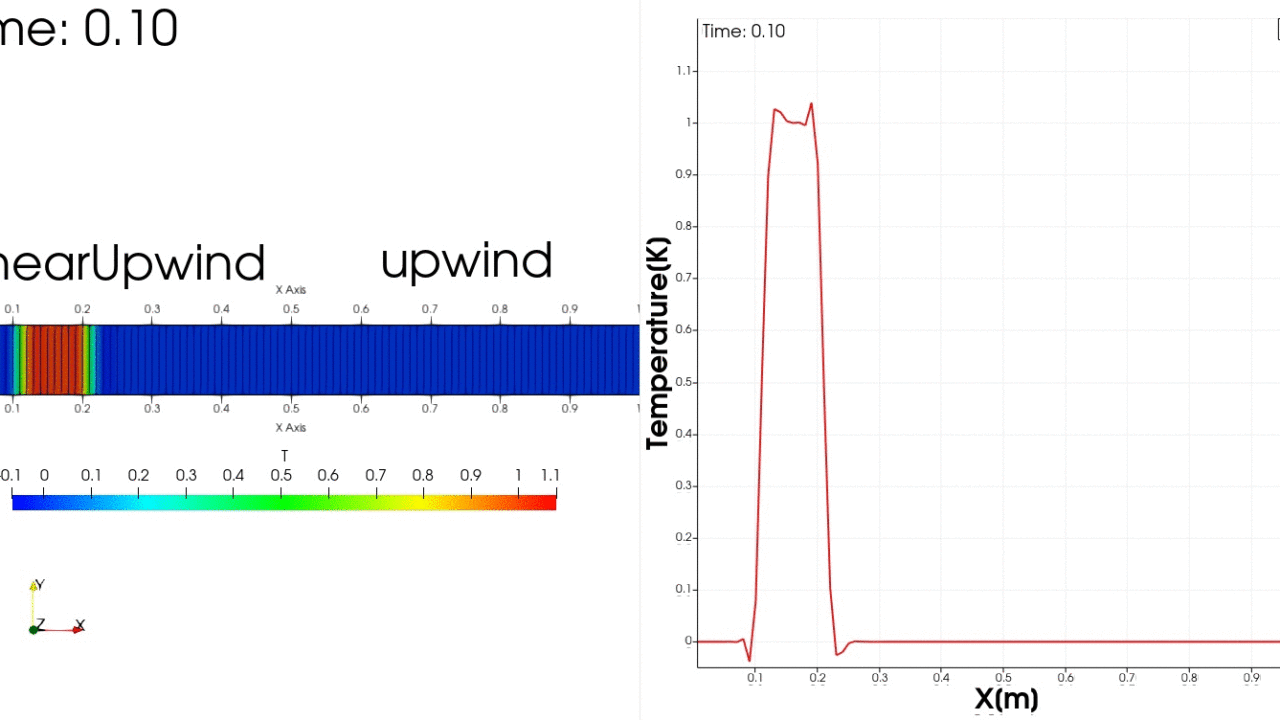
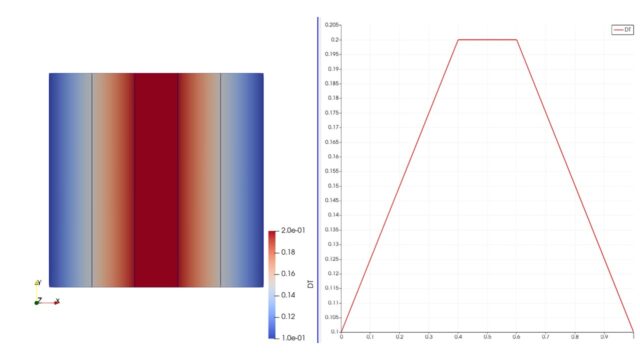
領域1では2次精度風上差分により多少振動する解の挙動が得られ、領域2では解は安定で振動は収まるが数値拡散が生じるという挙動を示すだろうと予測できます。

結果

結果は$0 \leq x <0.5$は解の形は保たれていますが少し振動しています。
$0.5 \leq x \leq 1.0$では振動は収まりますがかなり数値拡散がひどくなっています。

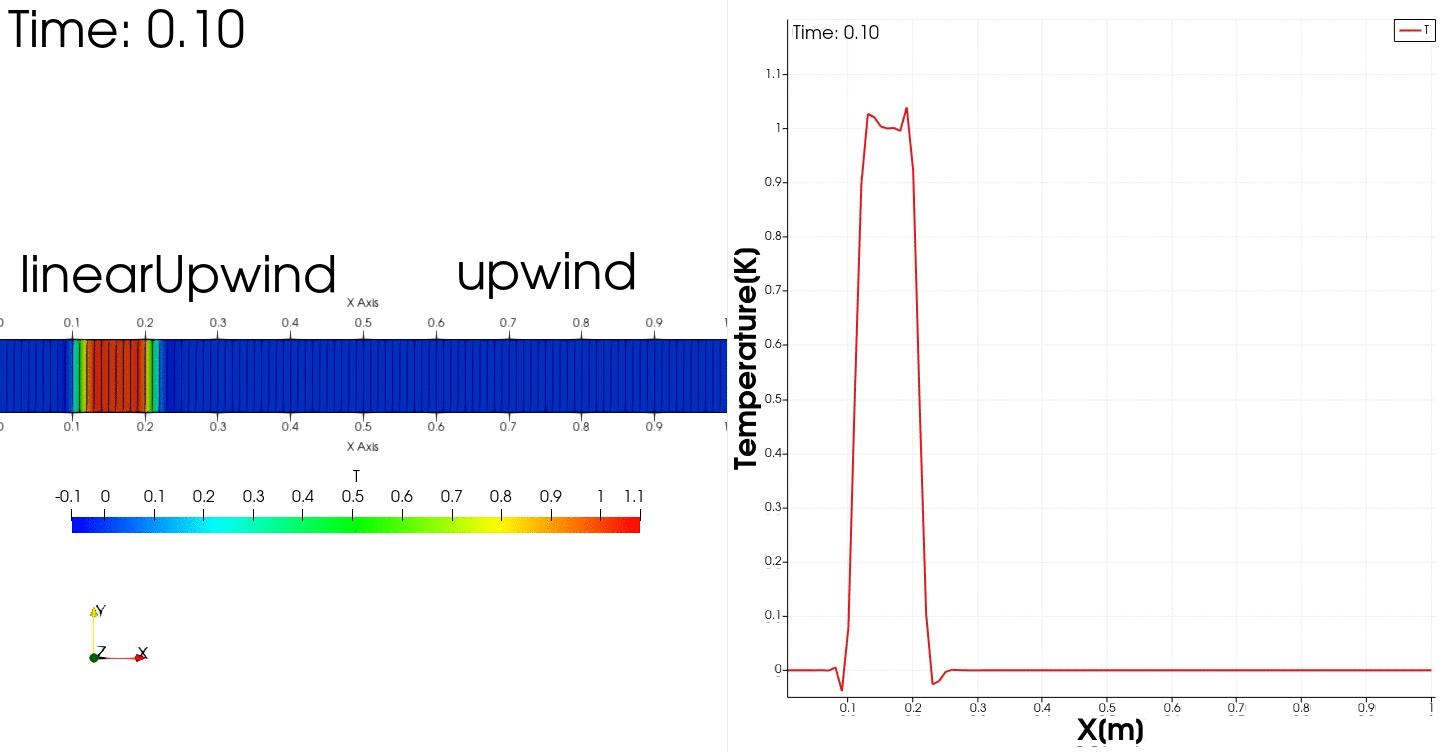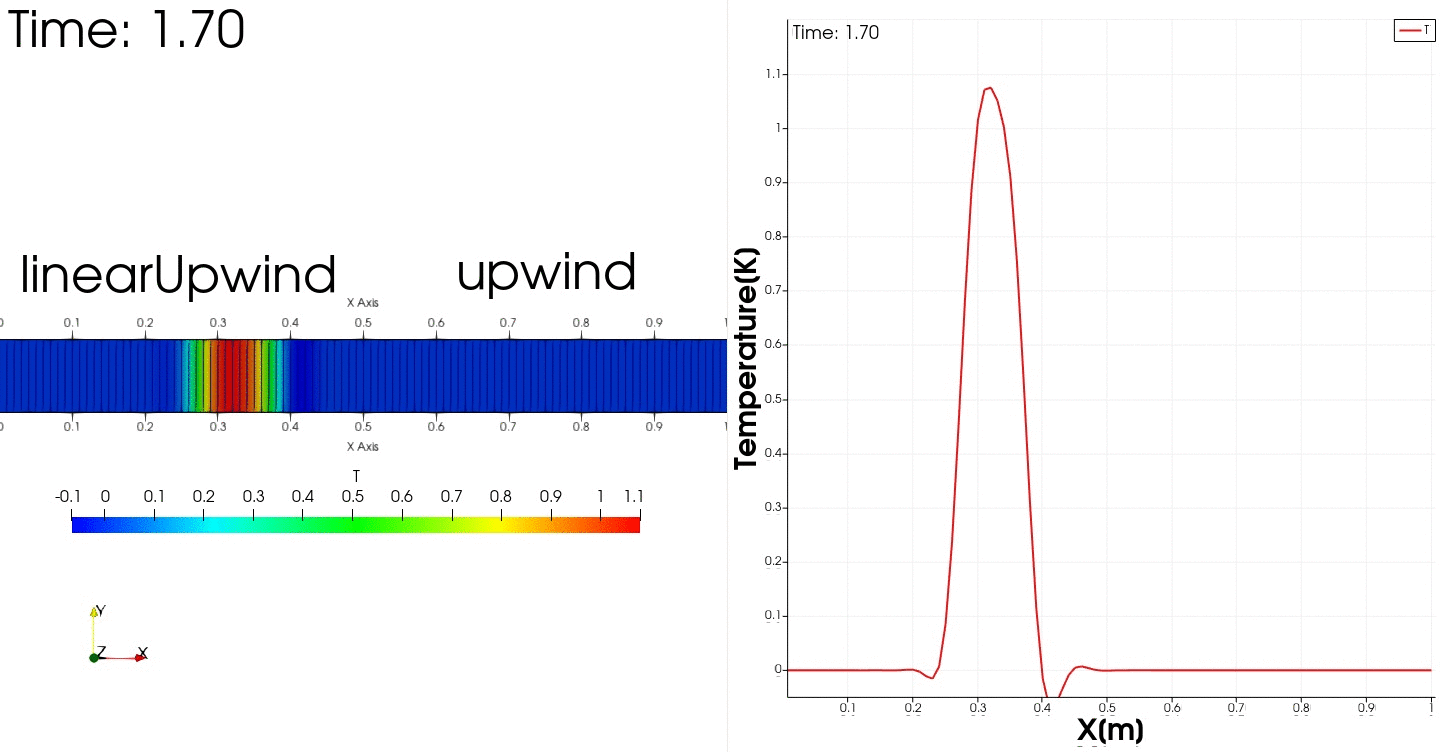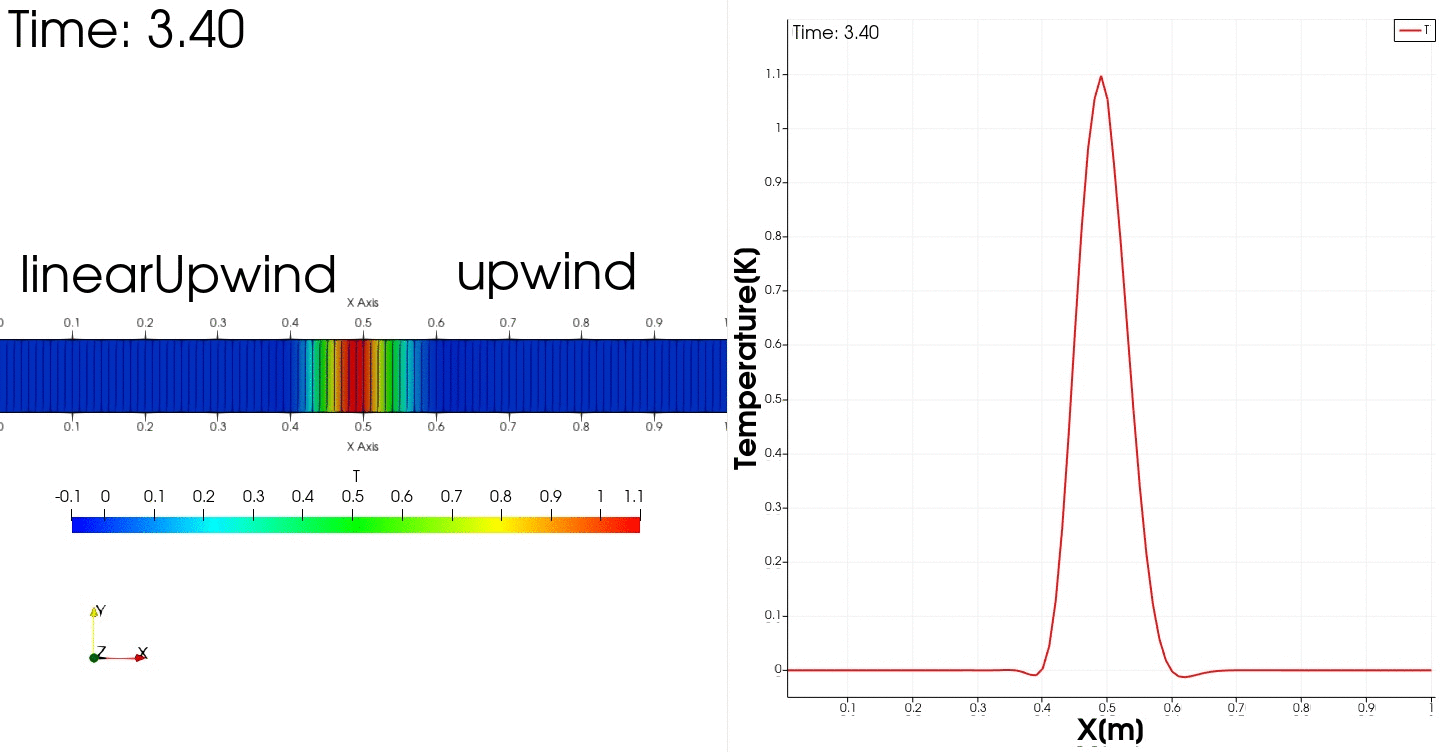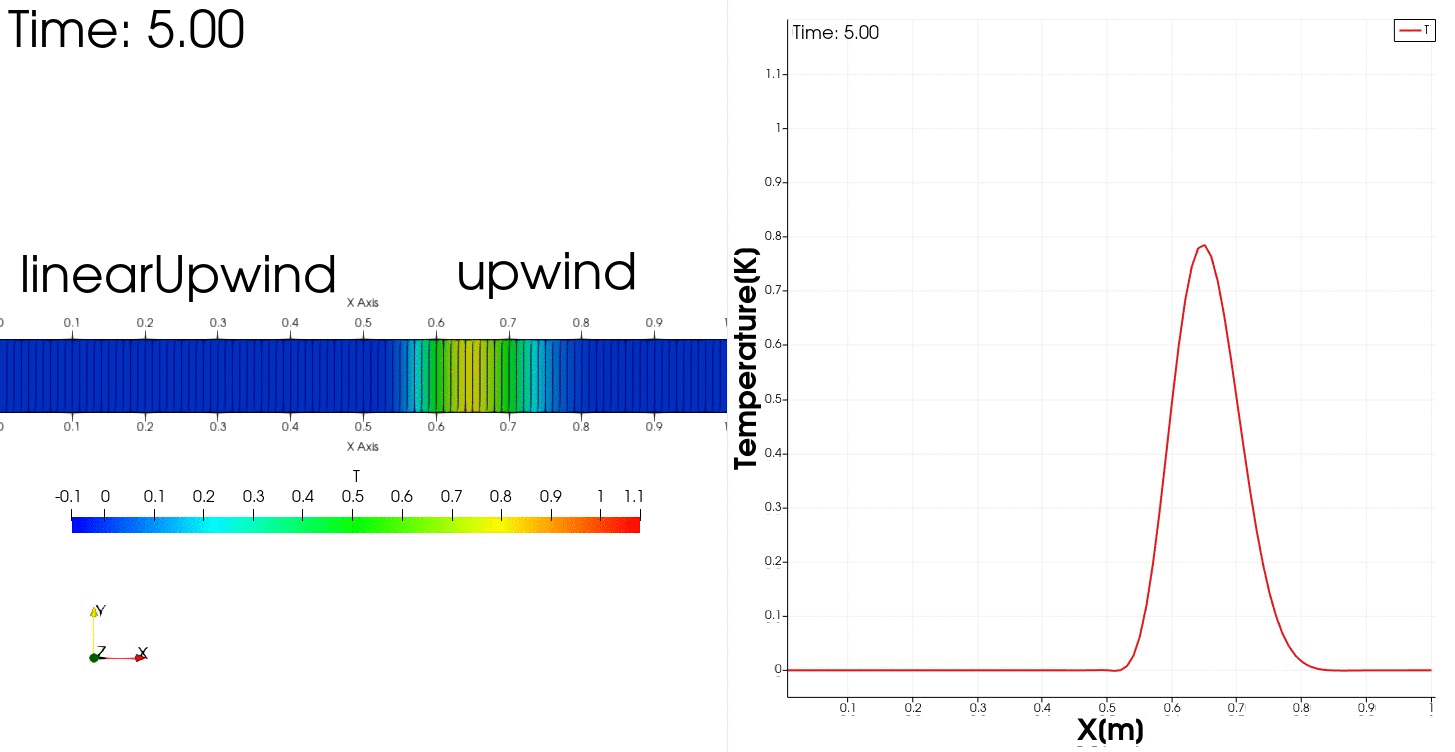
このようにzoneBlendedを使用することで領域ごとにスキームを変えることができました。

まとめ

今回の記事では、OpenFOAM v2412の新機能zoneBlended を活用し、1次元移流方程式の数値計算で領域ごとに異なる対流項スキームを適用する方法を紹介しました。

実装方法
1. FaceZoneの作成（system/topoSetDict）で領域を分割。
2. スキームの設定（system/fvSchemes）で zoneBlended を用い、
  - 領域1：線形風上差分（2次精度）
  - 領域2：風上差分（1次精度）
    を適用。

このように、数値計算ではスキームの選択が解の精度や安定性に大きく影響するため、シミュレーションの目的に応じて適切に設定することが重要です。

移流方程式を領域ごとにスキームを変えてみた。
x=0~0.5：2次精度線形風上差分
x=0.5~1.0：風上差分

faceZoneを作って対流項スキームを変える。
使い道わからないけど発散しやすいところにあえて風上差分で数値粘性効かすとか？https://t.co/oZ60nInplm pic.twitter.com/TBICTdPFsL

— カマキリ🐲CAE頑張る (@t_kun_kamakiri) February 17, 2025