【演習問題1：大学院入試問題】解析力学：棒の微小運動の問題をラグランジュ方程式から求める

どうも(^^)/

せっかく今まで解析力学を学んできたので、少し演習問題を通じて「こんな風に使うのか」というように理解を深めたいと思います。

まずは簡単な問題から！

問題

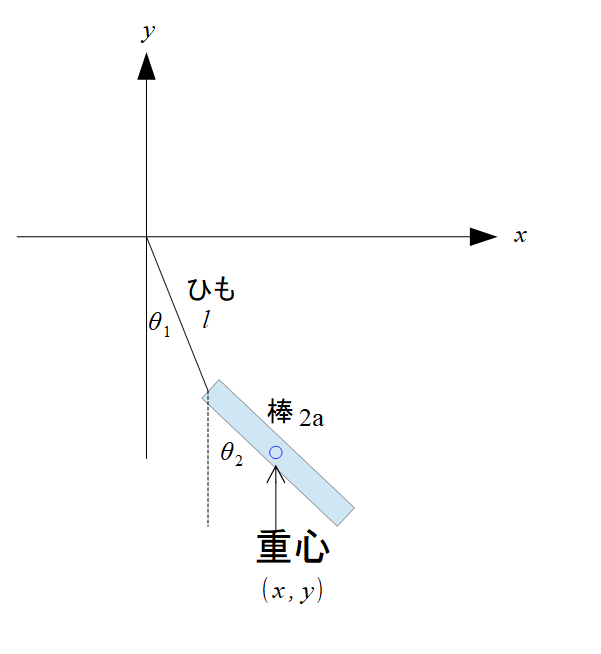
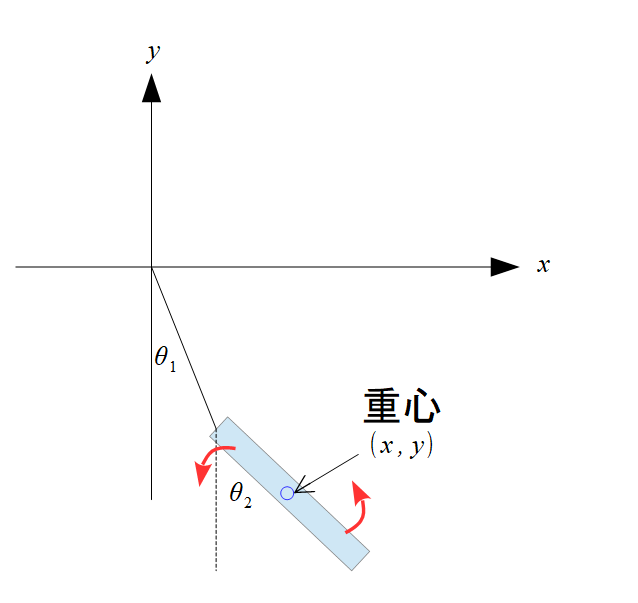
固定点からつるした長さ$l$のひもの先端に質量$m$、長さ$2a$の一様な棒をつるします。
この棒を鉛直面内で微小運動させたときの運動を求めなさい。

絵にするとこんな感じです。

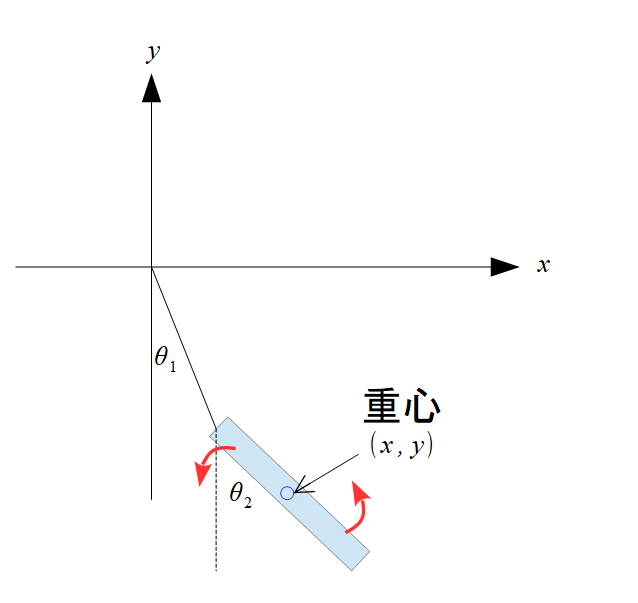
微小運動と言っているので実際は、↓こんな感じです(笑)

微小運動と言っているのは、そうしないと手計算で解きにくいっているのもあります。

$\theta_{1}$、$\theta_{2}$が微小と言っているので、

$\cos\theta\simeq 1-\frac{\theta^2}{2}$

$\sin\theta\simeq \theta$

↑これが使えます。
※テーラー展開の最小次数のみ残します。

まずは解き方の方針を示しましょう!(^^)!

方針
運動エネルギーとポテンシャルエネルギーを求める
1. 運動エネルギー
2. ポテンシャルエネルギー
ラグランジアン$L$を求める
ラグランジュ方程式
(9)式を(11)(12)式に代入して運動方程式を導く
微分方程式(13)(14)を解く
まとめ
参考図書

方針

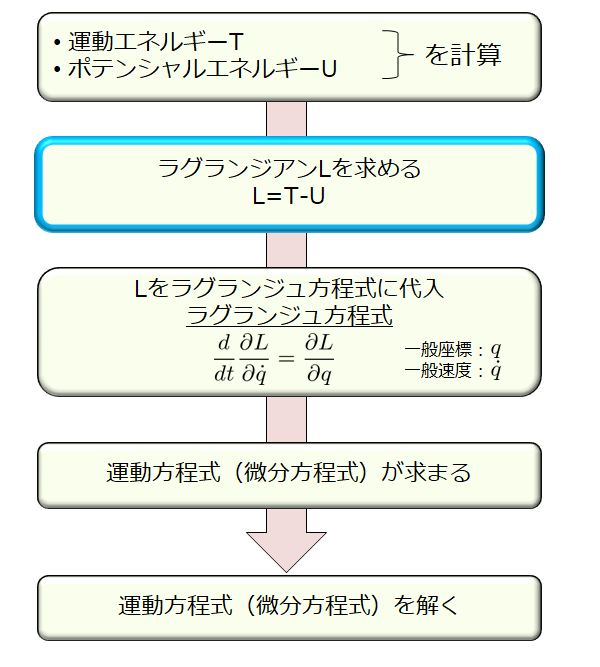
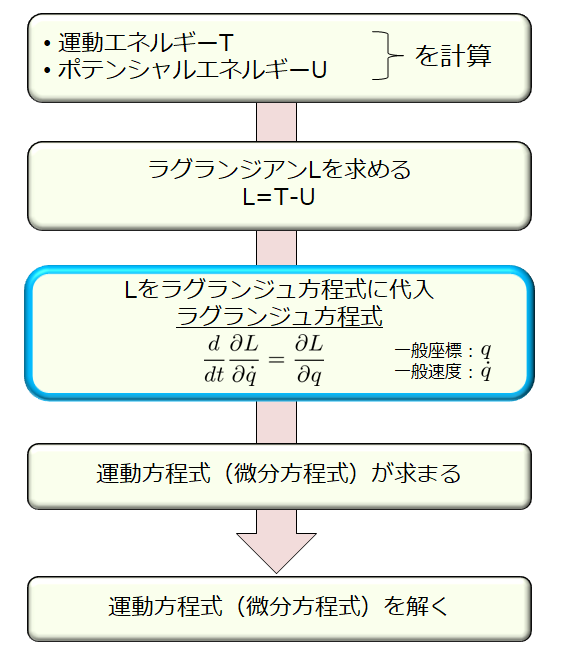
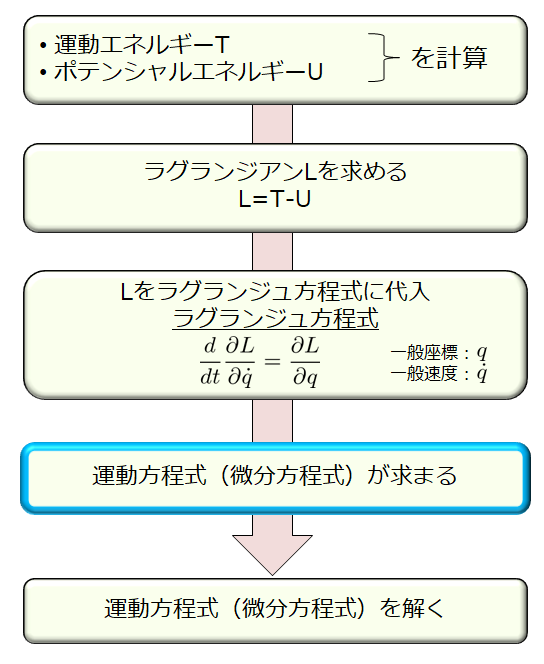
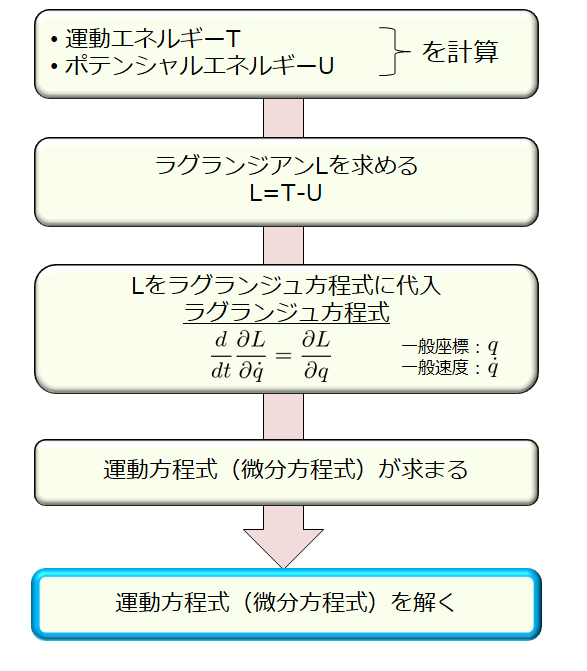
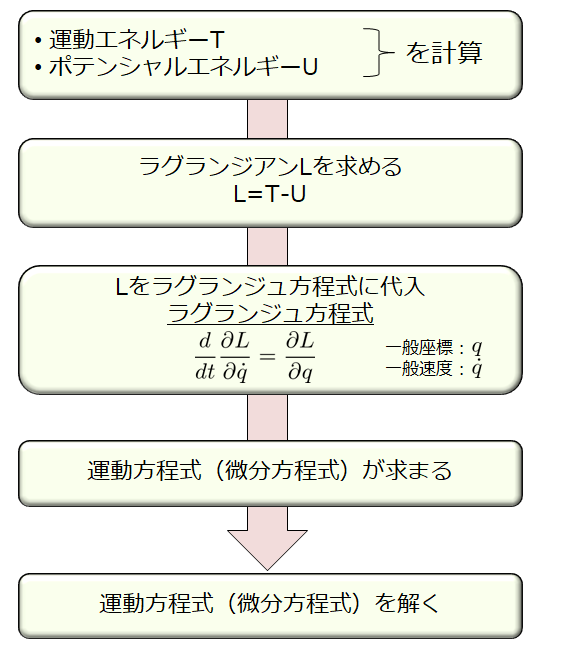
この問題をどういった流れで解くのかをイメージしておく方が良いです。

大学院の入試問題で出題される典型的な解析力学の問題では、ほとんどが下記の流れに従って解けると思っています。

全体の流れを確認したところで、さっそく解いていきましょう(^^)/

運動エネルギーとポテンシャルエネルギーを求める

運動エネルギー

まず運動エネルギーを求めます。

ここで注意しなくてはいけないのですが、

※注意点その1

運動エネルギー=重心の並進運動エネルギー＋重心回りの回転運動エネルギー

と、このように考えなければなりません。

高校の物理までのノリでいけば、運動エネルギーといえば「並進運動エネルギー」だけ考えがちなのですが、それは質点（大きさがなく質量だけある状態）を考えたときの言わば”存在しない仮想的なもの”で考えた場合での話です。

今回は形があるので、物体の回転の運動エネルギーも考慮しなくてはいけません。

※注意点その2

”重心”の並進運動エネルギーと”重心”回りの回転運動エネルギー

↑重心を基準にして考えましょう。

なぜかと言いますと、重心からずれた場合の慣性モーメントを考えるのはちょっと面倒です。
平衡軸の定理を使えば慣性モーメントを求められるのですが・・・・

重心回りの慣性モーメントなら、簡単に求めまれます。

今回の棒の慣性モーメントならとても簡単です。

慣性モーメント$I=\frac{1}{12}m(2a)^2=\frac{1}{3}ma^2$です。ちなみに慣性モーメントは、回転のしにくさを表す量になります。

では、運動エネルギーを求めます。

棒の重心座標を示します。

\begin{align*}x=l\sin\theta_{1}+a\sin\theta_{2}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}y=-l\cos\theta_{1}-a\cos\theta_{2}\cdot\cdot\cdot (2)\end{align*}

↑とても素直に計算するだけです。

運動エネルギーを求めるのに、(1)(2)を時間微分しておく必要があります。

\begin{align*}\dot{x}=l\dot{\theta_{1}}\cos\theta_{1}+a\dot{\theta_{2}}\cos\theta_{2}\cdot\cdot\cdot (3)\end{align*}

\begin{align*}\dot{y}=l\dot{\theta_{1}}\sin\theta_{1}+a\dot{\theta_{2}}\sin\theta_{2}\cdot\cdot\cdot (4)\end{align*}

重心の並進運動エネルギー

\begin{align*}\frac{1}{2}m(\dot{x}+\dot{y})=\frac{1}{2}\big((l\dot{\theta_{1}}\cos\theta_{1}+a\dot{\theta_{2}}\cos\theta_{2})^2+(l\dot{\theta_{1}}\sin\theta_{1}+a\dot{\theta_{2}}\sin\theta_{2})^2\big)^2\end{align*}

\begin{align*}=\frac{1}{2}m\big(l^2\dot{\theta_{1}}^2+a^2\dot{\theta_{2}}^2+2al(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})\dot{\theta_{1}}\dot{\theta_{2}}\big)\cdot\cdot\cdot (5)\end{align*}

重心回りの回転運動エネルギー

\begin{align*}\frac{1}{2}I\dot{\theta_{2}}^2=\frac{1}{6}ma^2\dot{\theta_{2}}^2\cdot\cdot\cdot (6)\end{align*}

(5)と(6)を足せば運動エネルギーの完成です。

運動エネルギー

\begin{align*}T=\frac{1}{2}m\big(l^2\dot{\theta_{1}}^2+a^2\dot{\theta_{2}}^2+2al(\cos\theta_{1}\cos\theta_{2}+\sin\theta_{1}\sin\theta_{2})\dot{\theta_{1}}\dot{\theta_{2}}\big)+\frac{1}{6}ma^2\dot{\theta_{2}}^2\end{align*}

\begin{align*}\simeq m(\frac{l^2\dot{\theta_{1}}^2}{2}+al\dot{\theta_{1}}\dot{\theta_{2}}+\frac{2a^2\dot{\theta_{2}}^2}{3})\cdot\cdot\cdot (7)\end{align*}

※↑$\theta$が微小だとして、$\cos\theta\simeq 1-\frac{\theta^2}{2}$、$\sin\theta\simeq \theta$としています。

ポテンシャルエネルギー

ポテンシャルエネルギーはどうでしょうか。

こちらは簡単です!(^^)!

ポテンシャルエネルギーというとわかりにくいですが、棒の位置エネルギーを考えることになります。

$y$軸のマイナス方向に重力$g$がかかっているとすれば、

\begin{align*}U=mgy=mg(-l\cos\theta_{1}-a\cos\theta_{2})\end{align*}

\begin{align*}\simeq \frac{1}{2}mg(l\theta_{1}^2+a\theta_{2}^2-l-a)\cdot\cdot\cdot (8)\end{align*}

↑どこを基準にとるかによって位置エネルギーは変わるのですが、ここでは座標の原点を基準に取りました。ポテンシャルの中にある定数$\frac{mg}{2}(-l+-a)$は定数であり、ポテンシャルの基準点を変えているので除いても構いません。

任意の点を基準に位置エネルギーをとっても良いですが、その後で求めるラグランジュ方程式には何の影響も及ぼさないことがわかります。
エネルギーというものは何を基準にするかによって値は変わるのですが、力学の運動の性質を変えているわけではないのです。

ラグランジュ方程式はラグランジアンの一般座標の微分があるのために、ポテンシャルエネルギーのような座標で決定している量の基準点を変えることによる影響は計算上出てきません。

なので(8)式は、

\begin{align*}U=\frac{1}{2}mg(l\theta_{1}^2+a\theta_{2}^2)+const\cdot\cdot\cdot (8.1)\end{align*}

としていても良いです。

ここでは、(8)式のままでもいきましょう。

さて、ラグランジアンを求める準備ができました。

ラグランジアン$L$を求める

ラグランジアン$L=T-U$は(7)(8)式より、

\begin{align*}L=m(\frac{l^2\dot{\theta_{1}}^2}{2}+al\dot{\theta_{1}}\dot{\theta_{2}}+\frac{2a^2\dot{\theta_{2}}^2}{3})-\frac{1}{2}mg(l\theta_{1}^2+a\theta_{2}^2)\cdot\cdot\cdot (9)\end{align*}

ラグランジュ方程式

ここでラグランジアン$L$の変数を確認しましょう。

\begin{align*}L=L(\theta_{1},\theta_{2},\dot{\theta_{1}},\dot{\theta_{2}})\end{align*}

となり、

変数は$\theta_{1},\theta_{2},\dot{\theta_{1}},\dot{\theta_{2}}$ですね。

なのでラグランジュ方程式は、

\begin{align*}\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{\theta_{1}}}=\frac{\partial L}{\partial \theta_{1}}\cdot\cdot\cdot (11)\end{align*}

\begin{align*}\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{\theta_{2}}}=\frac{\partial L}{\partial \theta_{2}}\cdot\cdot\cdot (12)\end{align*}

と、この２つです。

(9)式を(11)(12)式に代入して運動方程式を導く

(11)より

\begin{align*}\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{\theta_{1}}}=\frac{\partial L}{\partial \theta_{1}}\cdot\cdot\cdot (11)\end{align*}

↓

\begin{align*}ml^2\ddot{\theta_{1}}+mal\ddot{\theta_{2}}=-mgl\theta_{1}\end{align*}

⇔

\begin{align*}l\ddot{\theta_{1}}+a\ddot{\theta_{2}}+g\theta_{1}=0\cdot\cdot\cdot (13)\end{align*}

(11)より

\begin{align*}\frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{\theta_{2}}}=\frac{\partial L}{\partial \theta_{2}}\cdot\cdot\cdot (11)\end{align*}

↓

\begin{align*}mal\ddot{\theta_{1}}+\frac{3}{4}ma^2\ddot{\theta_{2}}=-mga\theta_{2}\end{align*}

⇔

\begin{align*}l\ddot{\theta_{1}}+\frac{3}{4}a\ddot{\theta_{2}}+g\theta_{2}=0\cdot\cdot\cdot (14)\end{align*}

というわけで運動方程式が(13)(14)のように求まりました!(^^)!

微分方程式(13)(14)を解く

\begin{align*}l\ddot{\theta_{1}}+a\ddot{\theta_{2}}+g\theta_{1}=0\cdot\cdot\cdot (13)\end{align*}

\begin{align*}l\ddot{\theta_{1}}+\frac{4}{3}a\ddot{\theta_{2}}+g\theta_{2}=0\cdot\cdot\cdot (14)\end{align*}

さてこの2つを求めていきましょう。

ちなみに、これらの微分方程式は2階の常微分方程式ですね。

ということは、解は2つの任意定数を含んだ形になります。

もし、任意定数を求めたければ初期の状態（位置や速度の2条件）を加えることで求まりますが、問題は「この棒を鉛直面内で微小運動させたときの運動を求めなさい。」なので任意定数を含んだ形が解になります。

(13)(14)の形の常微分方程式の解法はよくあるパターンで、特殊解は振動解のような形です。

例えば、$\cos\omega t$、$\sin\omega t$、$e^{i\omega t}$のような形が解になります。

ここでは、特殊解を$\theta_{1}=Ae^{i\omega t}$、$\theta_{2}=Be^{i\omega t}$と置いて(13)(14)に代入し、$\omega$を求めます。

\begin{align*}\dot{\theta_{1}}=Ai\omega e^{i\omega t}\end{align*}

\begin{align*}\ddot{\theta_{1}}=-A\omega^2e^{i\omega t}\end{align*}

\begin{align*}\dot{\theta_{2}}=Bi\omega e^{i\omega t}\end{align*}

\begin{align*}\ddot{\theta_{2}}=-B\omega^2e^{i\omega t}\end{align*}

なので、

\begin{align*}(g-l\omega^2)A-a\omega^2B=0\cdot\cdot\cdot (15)\end{align*}

\begin{align*}-l\omega^2A+(g-\frac{4}{3}a\omega^2)B=0\cdot\cdot\cdot (16)\end{align*}

⇔行列で記述

\begin{align*}\begin{pmatrix}g-l\omega^2 & -a\omega^2\\ -l\omega^2 & g-\frac{4}{3}a\omega^2\end{pmatrix}\begin{pmatrix}A \\ B\end{pmatrix}=0\cdot\cdot\cdot (17)\end{align*}

$A=B=0$で以外の解があるためには(17)の係数の行列式が０でないといけません。

ゆえに、

\begin{align*}\begin{vmatrix}g-l\omega^2 & -a\omega^2\\
-l\omega^2 & g-\frac{4}{3}a\omega^2\end{vmatrix}=0\end{align*}

この行列式の計算は、下記のように「赤同士の掛け算ー青同士の掛け算=0」で求まります。

⇔$\omega^2$に関する2次方程式

\begin{align*}al\omega^4-g(3l+4a)\omega^2+3g^2=0\end{align*}

∴

\begin{align*}\omega^2=\frac{3l+4a\pm \sqrt{(3l+4a)^2-12al}}{2al}\end{align*}

２つ解が出てきました。

それらをそれぞれ$\omega_{1}^2$、$\omega_{2}^2$と置きます。

\begin{align*}\omega^2_{1}=\frac{3l+4a+ \sqrt{(3l+4a)^2-12al}}{2al}g\cdot\cdot\cdot (18)\end{align*}

\begin{align*}\omega^2_{2}=\frac{3l+4a- \sqrt{(3l+4a)^2-12al}}{2al}g\cdot\cdot\cdot (19)\end{align*}

※平方根の中身は正の値ですので、$\omega_{1}^2$は実数。

(18)(19)を(15)(16)に代入すると、$\omega_{1}^2$に対する$A$と$B$の値、$\omega_{2}^2$に対する$A$と$B$の関係式が求まります。

$\omega_{1}$に対して$A_{1}$、$B_{1}$

\begin{align*}\frac{A_{1}}{B_{1}}=\frac{a\omega_{1}^2}{g-l\omega_{1}^2}\end{align*}

$\omega_{2}$に対して$A_{2}$、$B_{2}$

\begin{align*}\frac{A_{2}}{B_{2}}=\frac{a\omega_{2}^2}{g-l\omega_{2}^2}\end{align*}

すると(13)(14)式の一般解が、

\begin{align*}\theta_{1}=A_{1}e^{i\omega_{1} t}+A_{2}e^{i\omega_{2} t}\end{align*}

\begin{align*}\theta_{2}=B_{1}e^{i\omega_{1} t}+B_{2}e^{i\omega_{2} t}\end{align*}

と求まりました。
※$\frac{A_{1}}{B_{1}}=\frac{a\omega_{1}^2}{g-l\omega_{1}^2}$
※$\frac{A_{2}}{B_{2}}=\frac{a\omega_{2}^2}{g-l\omega_{2}^2}$

$\omega$の符号が気になるところかもしれませんが、これは初期条件などを決めるとどちらか片方に決まるのではないでしょうかね。

（要するに、$\omega$の符号は$A$、$B$に含まれている。）

なので、$\omega$はここでは大きさが重要であると言えます。

まとめ

大学院の入試問題であるこの手の問題は、ラグランジュ方程式を用いると簡単に解を求めることができます。

ラグランジュ方程式を用いない場合は、

\begin{align*}l\ddot{\theta_{1}}+a\ddot{\theta_{2}}+g\theta_{1}=0\cdot\cdot\cdot (13)\end{align*}

\begin{align*}l\ddot{\theta_{1}}+\frac{4}{3}a\ddot{\theta_{2}}+g\theta_{2}=0\cdot\cdot\cdot (14)\end{align*}

↑この運動方程式自体を自力で求めないといけないことになります。

結構めんどそうですよね。

ラグランジアンを求めてラグランジュ方程式に代入すれば運動方程式を得ることができるという知見を解析力学で学んだので、この記事で示したように解析力学の力を借りた方が断然問題は解きやすいです。

解析力学という学問自体が、座標系に依らない一般的な形式を目指したものですのですので、当然「デカルト座標表示」でも「極座標表示」でも解を求めるまでの流れは同じです。

ここが、解析力学の利点であって通常の力学とは異なるところですよね。

（力学だと座標系が変わると表記が変わります。念のため補足ですが、表記が変わっただけであくまで$ma=F$という物理法則そのものがかわっているわけではありません。量子力学や相対性理論のように物理法則の式そのものを書き換えるのとは違います。量子力学も相対性理論も極限をとったら古典力学と同じ法則になってくれていないと困るのですがね）

この手の問題の解法の流れは以下です。
この流れを覚えておくと良いでしょう!(^^)!