ラグランジュ未定乗数法　例題演習：解析力学とのつながり

どうも(^^)

本記事はもともと、「ランダウ=リフシッツの”力学”をいきなり読むと挫折する説」というタイトルから始まり、なぜ挫折するのかを解説してきました。

前回の記事はこちら

いきなりランダウ=リフシッツの力学を読んだら物理で絶望する説

上の記事で詳しく書いてあるのですが、理由はシンプルで「これは一般的に言う”力学”の教科書ではなく”解析力学”だからなのです。」

ということでした。

それから、第3報まではラグランジュ方程式を導くための解説をしましたが、前回なぜか下記のように
突然「ラグランジュ未定乗数法」というお話をし出しました。

前回の記事はこちら

ラグランジュ未定乗数法：解析力学とのつながり

理由は、”力学”や”解析力学”とは関係なく以下のように考えてみたらどうなるのかを示したいと考え始めたからです。

「ある関数\(U(x,y)\)がある拘束条件\(g(x,y)=0\)もとで最小となる場合を考えた時、どのような式が導かれるか？」

↓その問いに答えてくれそうなのが数学的には、

あらゆる仮想の変位\(\delta x\)、\(\delta y\)に対して

\begin{align*}\frac{\partial U}{\partial x}+\lambda\frac{\partial g}{\partial x}=0\end{align*}

\begin{align*}\frac{\partial U}{\partial y}+\lambda\frac{\partial g}{\partial y}=0\end{align*}

という式になります。これをラグランジュ未定乗数法といいます。

↑上の2式が物理学でいうところの何になるかは、次回以降の記事で示すことにして、

本記事の目標

ラグランジュ未定乗数法を使って問題演習をしてみましょう(^^)/

問題：

「\(x^2+2xy+y^2=1\)の条件のもとで、\(U(x,y)=x^2+3y^2\)が極値をもつ点\((x,y)\)を求めよ」

方針
(2)式を使うため偏微分を実行
(1)式の拘束条件に代入
答え
番外編：極値ってだけで最小じゃない？
最小か最大か見てみよう
まとめ
ところで・・・
次回
参考図書

方針

問題は、

拘束条件\(g(x,y)=x^2+2xy+y^2-1\)とおけば、
\(g(x,y)=0\)のもとで、\(U(x,y)=x^2+3y^2\)が極値をもつ点\((x,y)\)を求めることになります。

したがって、前回示したように、

\begin{align*}g(x,y)=0\cdot\cdot\cdot (1)\end{align*}

の条件のもと、

\begin{align*}\frac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}}=\frac{\frac{\partial g}{\partial x}}{\frac{\partial g}{\partial y}}=\lambda\cdot\cdot\cdot (2)\end{align*}

を満たす\((x,y)\)を探せばよいだけです。

(2)式を使うため偏微分を実行

まずは(2)式を使うために、\(U(x,y)\)、\(g(x,y)\)それぞれ偏微分しましょう。

\begin{align*}
\left\{\begin{matrix}
\frac{\partial U}{\partial x}=2x\\
\frac{\partial U}{\partial y}=6y\tag{3}
\end{matrix}\right.
\end{align*}

となります。

\begin{align*}
\left\{\begin{matrix}
\frac{\partial g}{\partial x}=2x+2y\\
\frac{\partial g}{\partial y}=2x+2y\tag{4}
\end{matrix}\right.
\end{align*}

\begin{align*}\end{align*}

、

これらを(2)式に代入して、

\begin{align*}\frac{2x}{6y}=\frac{2x+2y}{2x+2y}\end{align*}

を満たす点(\(x,y\))が、今回求める点です。

つまり、

\begin{align*}
x=3y\tag{5}
\end{align*}

となります。

(1)式の拘束条件に代入

あとは、出てきた(5)式を(1)式の拘束条件に代入すれば解けますね(^^)

\(x=3y\)のとき、

\begin{align*}(3y)^2+2(3y)y+y^2-1=0\end{align*}

より、

\begin{align*}
y=\pm \frac{1}{4}\tag{6}
\end{align*}

となります。

答え

ゆえに、拘束条件\(g(x,y)=0\)のもとで、\(U(x,y)=x^2+3y^2\)が極値となる点は、

\begin{align*}(x,y)=\bigg(\frac{3}{4},\frac{1}{4}\bigg)\end{align*}

と、

\begin{align*}(x,y)=\bigg(-\frac{3}{4},-\frac{1}{4}\bigg)\end{align*}

と2つ出てきましたね。

これが答えです。

一応、そのときの\(U\)の値も求めておくと、

\begin{align*}U\bigg(\pm \frac{3}{4},\pm \frac{1}{4}\bigg)=\frac{3}{4}\end{align*}

となります。

なんともあっさりと(笑)

答えがあっているか確認してみましょう！

無料で使えるこちらのソフトで確認を行いました。

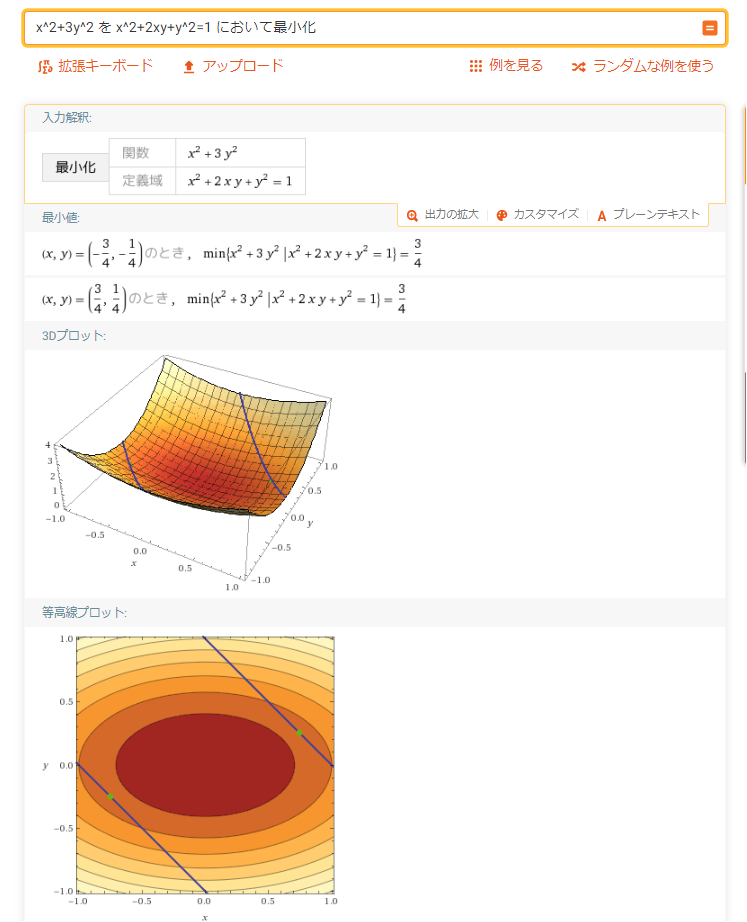
どうやら答えはあっているようですね。
無料ソフトなのに可視化してくれてめちゃくちゃわかりやすいです。

問題演習は以上となります。

感覚はつかんで頂けましたしょうか？

番外編：極値ってだけで最小じゃない？

答えは出たのですが・・・

僕は、最初から「ある拘束条件\(g(x,y)=0\)のもと\(U(x,y)=0\)が最小となる点」を求めたかったのに、

これじゃあ極値（停留点）をもとめただけで、”最大か最小かも区別できないじゃないか”ってことになっています。

証明は簡単なので、以下にさらっと示しておきましょう(^^)/

なにも難しいことを考えずに、変分\(\delta x\)、\(\delta y\)、つまりちょっとずらしたときに\(U(x,y)\)が増加しているのか減少しているのかを区別すれば良いだけです。

\begin{align*}U(x+\delta x,y+\delta y)-U(x,y)\end{align*}

↑こいつの大小を見ればよいはず！・・・（☆）

では、

\begin{align*}U(x+\delta x,y+\delta y)\end{align*}

を\(\delta x\)、\(\delta x\)の2次の項までテーラー展開してみましょう。

\begin{align*}U(x+\delta x,y+\delta y)=U(x,y)+\frac{\partial U}{\partial x}\delta x+\frac{\partial U}{\partial y}\delta y+\frac{1}{2}\frac{\partial ^2U}{\partial x^2}\delta x^2+\frac{\partial ^2U}{\partial xy}\delta xy+\frac{1}{2}\frac{\partial ^2U}{\partial y^2}\delta y^2\end{align*}

と、こうなります。

ところで、今は極値のまわりの点\((x,y)\)でテーラー展開しようとしているのですから、
当然・・・

\begin{align*}\frac{\partial U}{\partial x}=\frac{\partial U}{\partial y}=0\end{align*}

です。

なので、

\begin{align*}U(x+\delta x,y+\delta y)-U(x,y)＝\frac{1}{2}\frac{\partial ^2U}{\partial x^2}\delta x^2+\frac{\partial ^2U}{\partial xy}\delta xy+\frac{1}{2}\frac{\partial ^2U}{\partial y^2}\delta y^2\end{align*}

となりました。

右辺がめちゃくちゃ見ずらいので、このように文字でおいてすっきりさせましょう。

\begin{align*}\frac{1}{2}\frac{\partial ^2U}{\partial x^2}=a\end{align*}

\begin{align*}\frac{\partial ^2U}{\partial xy}=b\end{align*}

\begin{align*}\frac{1}{2}\frac{\partial ^2U}{\partial y^2}=c\end{align*}

\begin{align*}\delta x=s\end{align*}

\begin{align*}\delta x=t\end{align*}

そうすると、右辺＝\(as^2+bst+ct^2\)なります。

(☆)に立ち返ると、\(as^2+bst+ct^2\)が正か負かを単純に見ればよいことになります。

\begin{align*}as^2+(bt)s+(ct^2)\end{align*}

とおけばどうですかね。
ただの\(s\)に関する2次関数ですね。

Q.\(t\)も変数じゃないかーー！！
A.\(t\)を固定したときに正か負かを知れば良いので、変数かどうかはこだわらなくても良いです。

Q.\(t\)に関する2次関数にしたらどうなるんだーー！！
A.式をみれば文字の置き方次第で\(s\)と\(t\)は対称なのでどちらに関する2次関数と見ても大して差し支えないです。

ここで、高校生の知識の登場です。

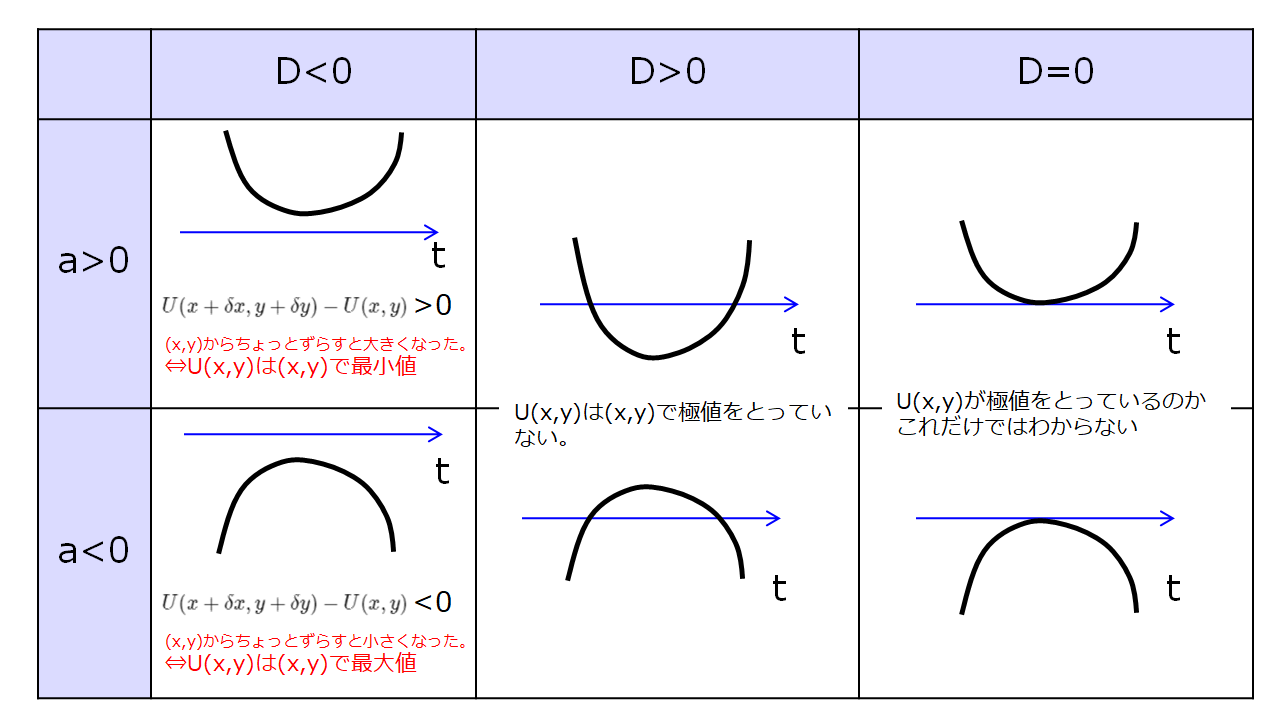
「判別式\(D=(bt)^2-4a(ct)=t^2(b^2-4ac)\)の正負を考えればよい。」

正の値t\(^2\)が邪魔なので、

「判別式\(D=b^2-4ac\)の正負を考えればよい。」

このようになりましたので、下記がその一覧です。

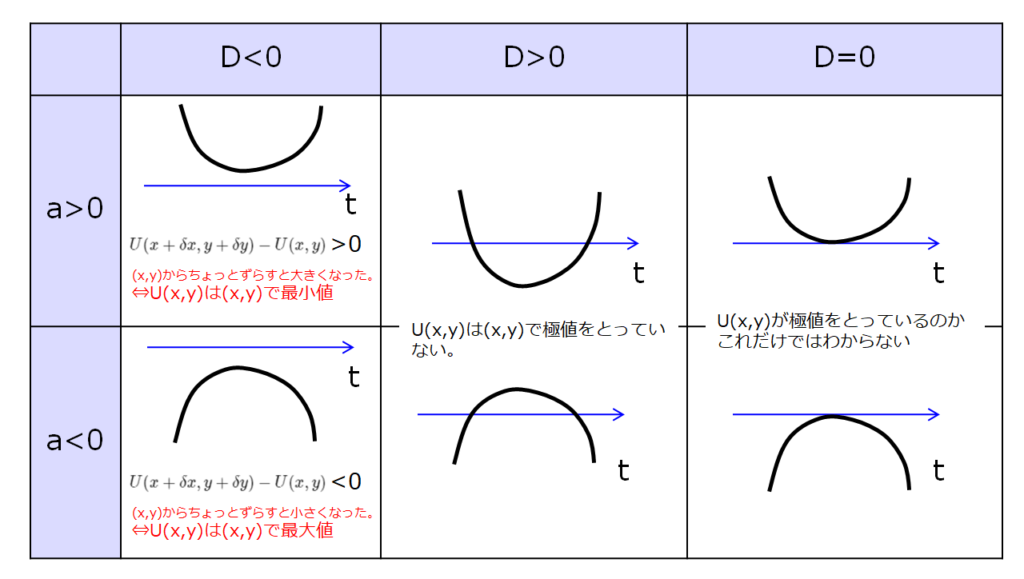
まとまりました(^^)

\(D>0\)や\(D=0\)なんかは、どの\(t\)に対しても正負がはっきり分かれているわけではないので、極値に対してはとても怪しい点という感じでしょうかね。

しかし、危ないですね。

\begin{align*}g(x,y)=0\cdot\cdot\cdot (1)\end{align*}

の条件のもと、

\begin{align*}\frac{\frac{\partial U}{\partial x}}{\frac{\partial U}{\partial y}}=\frac{\frac{\partial g}{\partial x}}{\frac{\partial g}{\partial y}}=\lambda\cdot\cdot\cdot (2)\end{align*}

を満たす\((x,y)\)を求める。

だけだと、極値をもとめる必要条件であって十分条件ではないということですね。

確かに、極小かなと思っても、停留しているだけでまた下がり始めるなんてこともありますし、確認は必要ということですかね。

最小か最大か見てみよう

では、上で示した考え方に従って最小か最大かを求めてみましょう。

まず2階微分が必要ですね。

\begin{align*}U(x,y)=x^2+3y^2\end{align*}

なので、

\begin{align*}a=\frac{1}{2}\frac{\partial^2 U}{\partial x^2}=1\end{align*}

\begin{align*}c=\frac{1}{2}\frac{\partial^2 U}{\partial y^2}=3\end{align*}

、

\begin{align*}\frac{\partial^2 U}{\partial xy}=0\end{align*}

ですね。

判別に従って計算すると、

\(D=b^2-4ac＝0^2-4\times 1\times 3<0\)、かつ\(a=1>0\)なので、

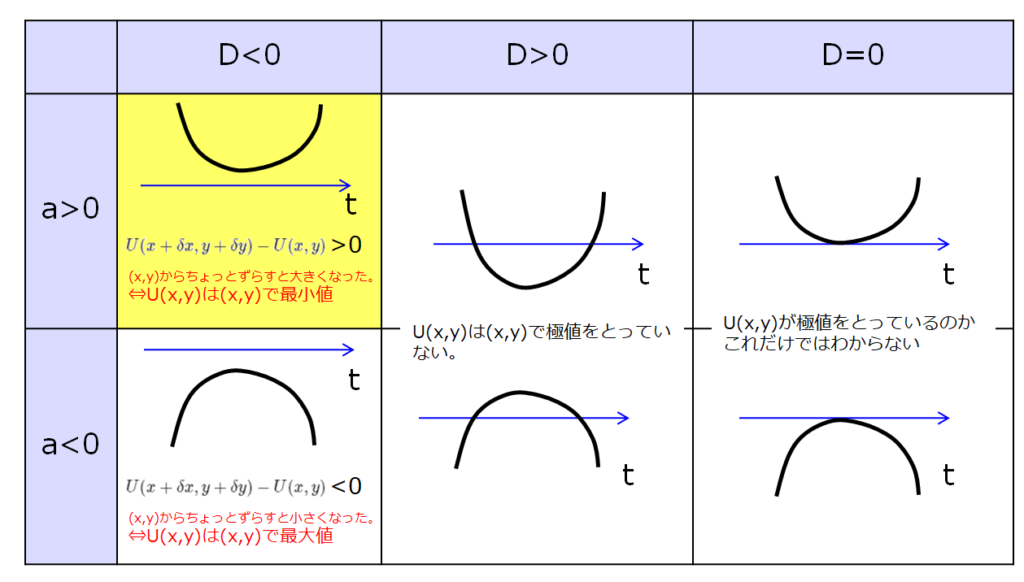
最小ですね！！

\begin{align*}U\bigg(\pm \frac{3}{4},\pm \frac{1}{4}\bigg)=\frac{3}{4}\end{align*}

は最小であることがわかりました。

まとめ

ラグランジュ未定乗数法を使って問題演習をしました。

ただ、「ラグランジュ未定乗数法だけでは極値をとるための条件であってそれが最小かどうかはわからない」ということを学びました。

ところで・・・

\begin{align*}U\bigg(\pm \frac{3}{4},\pm \frac{1}{4}\bigg)=\frac{3}{4}\end{align*}

は最小とわかったのですが、なぜ・・・

\begin{align*}(x,y)=\bigg(\frac{3}{4},\frac{1}{4}\bigg)\end{align*}

と、

\begin{align*}(x,y)=\bigg(-\frac{3}{4},-\frac{1}{4}\bigg)\end{align*}

最小となるのが２つでてきたのでしょう？？

それから、

\begin{align*}x=3y\cdot\cdot\cdot (5)\end{align*}

の意味は何でしょうかね？

これらは、読者の考察にゆだねるとしてここらへんで終わっておきます(^^)/

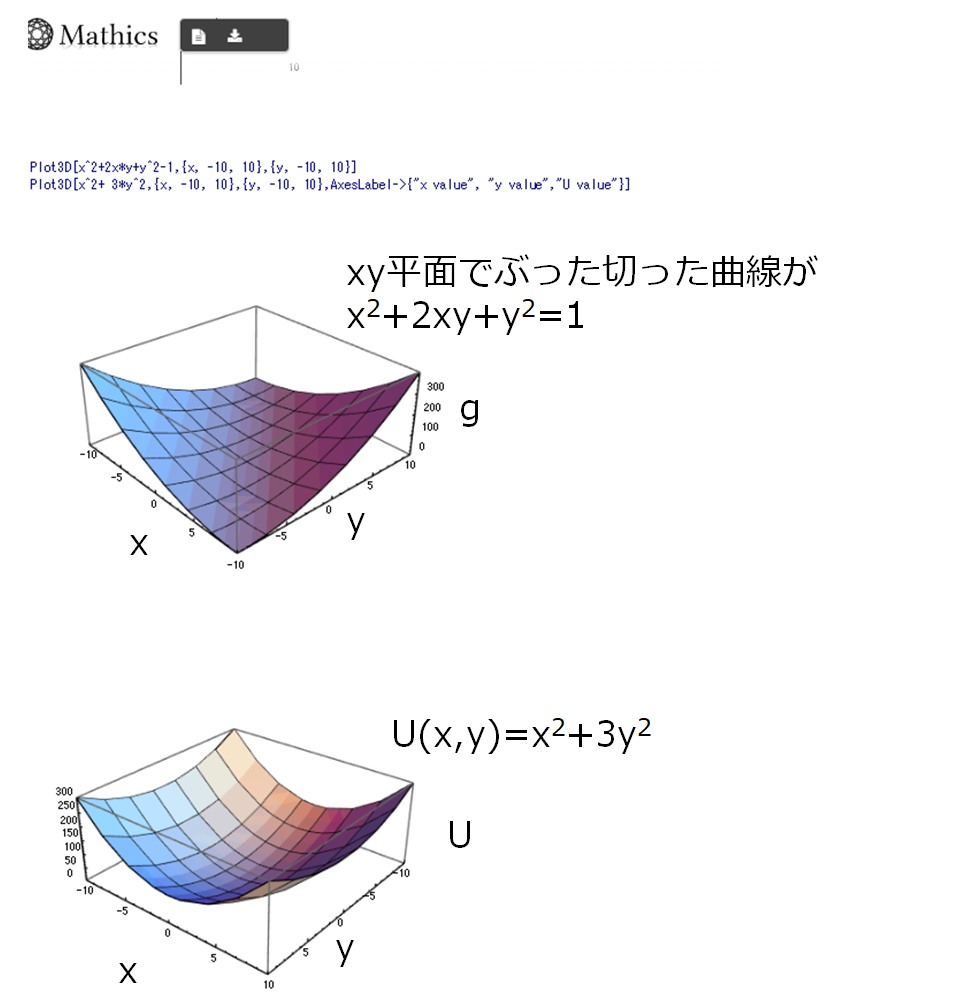
そういえば、問題演習であつかったものを3次元グラフにするとこんな感じです。

次回

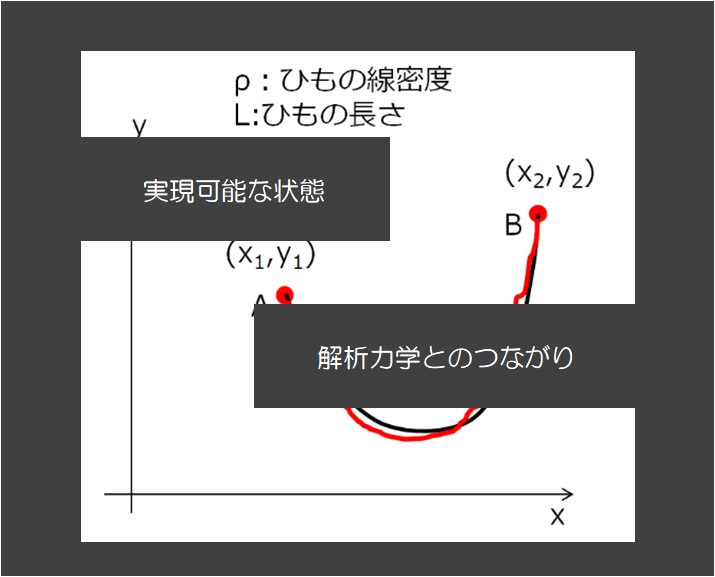
次回こそ、ひもの拘束の例題でラグランジュ未定乗数法を使って
「どのような状態が実現するか？」を示したいと思います。

↓これ。

前回の記事はこちら

ラグランジュ未定乗数法　実現可能な状態：解析力学とのつながり

参考図書

いくつかおすすめの解析力学の参考書を挙げておきます。

ランダウ力学

力学 (増訂第3版) ランダウ=リフシッツ理論物理学教程

エリ・ランダウ, イェ・エム・リフシッツ

2,200円(11/21 22:15時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)

L.D.ランダウ, E.M.リフシッツ

1,650円(11/21 16:46時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

下記のような小教程もあります。

解析力学：マセマキャンパスゼミ

解析力学キャンパス・ゼミ改訂3

馬場敬之

4,480円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。

著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。

その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。

解析力学ⅠⅡ：朝倉物理学大系

解析力学1 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,160円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

解析力学2 (朝倉物理学大系)

義隆, 山本, 孔一, 中村

6,380円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

この2冊は解析力学の名著ですね。

数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。

詳解力学演習

2,750円(11/21 11:20時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。

POSTED COMMENT

佐藤壮竜より:

2020年5月27日 19:23

答えが完全に間違っています。

返信
- korokoro より:
  
  2020年5月27日 23:05
  
  ご指摘ありがとうございます。
  完全に間違っていました！訂正致しました。
  ありがとうございます。
  
  返信
tokudai より:

2020年6月18日 20:38

x=-yが出てきた理由を知りたいです。

返信
- korokoro より:
  
  2020年6月18日 20:54
  
  コメントありがとうございます。
  すみません。誤記です。ｌ
  色々修正した中で記述が残ってしまっていただけです。
  
  混乱させて申し訳ございませんでした。
  
  返信