こんにちは(@t_kun_kamakiri)。
前回の記事では、「2次元のバーガース方程式」をGoogle Colabでアニメーション作成を行いました。
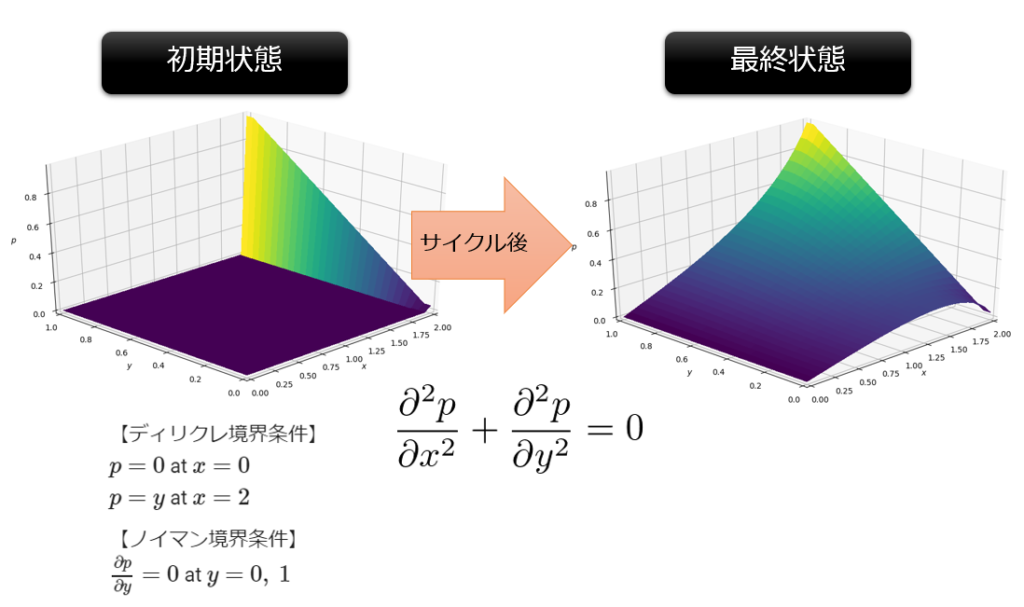
今回は、以下のような2次元のラプラス方程式をPythonで実装します。
本件の基本的な内容はこちらのサイトにそってやっていきます。
この記事ではこんな人を対象にしています。
- Pythonを使い始めたけどどう使うかわからない
- 流体の数値計算をはじめて勉強する人
- 2次元のラプラス方程式の数値的解法をなぜ知る必要があるのか
- 2次元のラプラス方程式の数値計算をPythonで実装
2次元のラプラス方程式
今回は以下のラプラス方程式ついてPythonを用いて実装して数値計算を行いたいと思います。
\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = 0
\tag{1}
\end{align*}
- ラプラス方程式とポアソン方程式の違い
- ナビエストークス方程式の数値計算にポアソン方程式を解く場面がある
ラプラス方程式とポアソン方程式の違い
ラプラス方程式の形をしていても、一般的には右辺が0ではない場合、
\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = f(x,y)\tag{2}
\end{align*}
をポアソン方程式と呼ばれています。
\nabla^2 \phi =-\frac{\rho(\boldsymbol{r})}{\epsilon}
\end{align*}
ナビエストークス方程式の数値計算にポアソン方程式を解く場面がある
ナビエストークス方程式の数値計算にポアソン方程式を解く場面があるからです。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
- ナビエストークスからは2本の式
- 連続の式から1つの式
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{8}
\end{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{9}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{10}
\end{align*}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) \tag{5}
\end{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)\tag{6}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{11}
\end{align*}
ラプラス方程式の離散化
くどいですが、今回の記事では☟こちらの方程式を扱う・・・・
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = b(x,y)\tag{12}
\end{align*}
b(x,y)=-\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{13}
\end{align*}
\end{align*}
\frac{p_{i+1, j}^n – 2p_{i,j}^n + p_{i-1,j}^n}{\Delta x^2} + \frac{p_{i,j+1}^n – 2p_{i,j}^n + p_{i, j-1}^n}{\Delta y^2} = 0
\end{align*}
p_{i,j}^n = \frac{\Delta y^2(p_{i+1,j}^n+p_{i-1,j}^n)+\Delta x^2(p_{i,j+1}^n + p_{i,j-1}^n)}{2(\Delta x^2 + \Delta y^2)}\tag{15}
\end{align*}
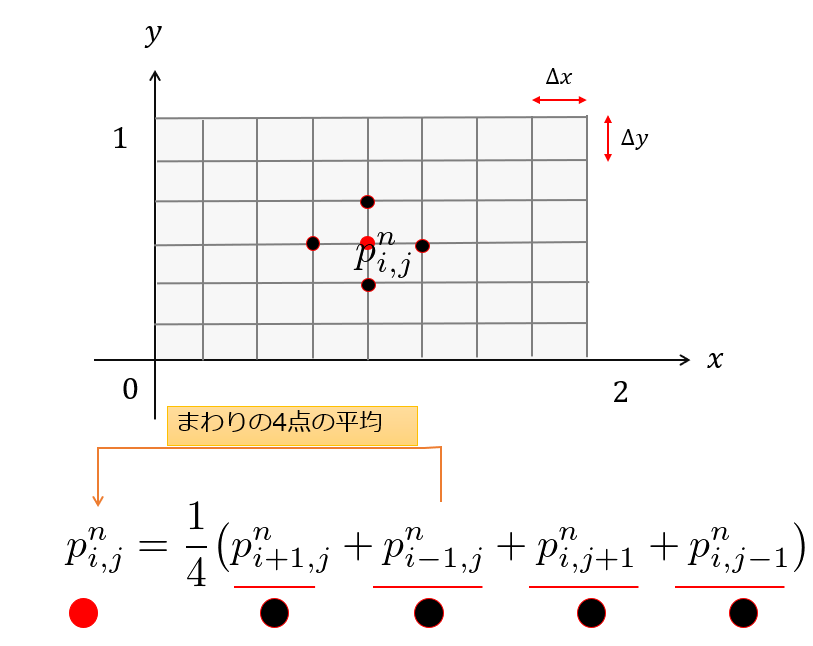
p_{i,j}^n = \frac{1}{4}\big(p_{i+1,j}^n+p_{i-1,j}^n+p_{i,j+1}^n + p_{i,j-1}^n\big)\tag{16}
\end{align*}
-
- \(p=0\) at
- \(x=0\)
- \(p=y\) at \(x=2\)
\(\frac{\partial p}{\partial y}=0\) at \(y=0, 1\)


p(x,y)=\frac{x}{4}-4\sum_{n=1,odd}^{\infty}\frac{1}{(n\pi)^2\sinh2n\pi}\sinh n\pi x\cos n\pi y\tag{17}
\end{align*}
ラプラス方程式のこいつがある意味がわかりません_(._.)_ pic.twitter.com/jS0F7vzF8Y
— カマキリ🐲@物理ブログ書いている (@t_kun_kamakiri) June 17, 2020
(ラプラス方程式は変数分離をして、境界条件を課すことでできるというのが僕の中の定石ですが、上手くいきませんでした_(._.)_)
ラプラス方程式をPythonで実装
【ポイント】
- 必要なライブラリをインポートする。
コードを以下のように書きます。
|
1 2 3 4 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import pyplot, cm from mpl_toolkits.mplot3d import Axes3D |
NumpyとMatplotlibをインポートします。
記述ミスがなければエラーなく進みます。
【ポイント】
- 初期状態を設定
- 境界条件を設定
コードを以下のように書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
nx = 31 ny = 31 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) ##initial conditions p = np.zeros((ny, nx)) # create a XxY vector of 0's ##plotting aids x = np.linspace(0, 2, nx) y = np.linspace(0, 1, ny) #境界条件 p[:, 0] = 0 # p = 0 @ x = 0 p[:, -1] = y # p = y @ x = 2 p[0, :] = p[1, :] # dp/dy = 0 @ y = 0 p[-1, :] = p[-2, :] # dp/dy = 0 @ y = 1 |
これで、初期状態の圧力のプロファイルができています。
初期状態と言っても、境界条件を課しただけですので初期の状態には何の意味もありません。
あくまで境界条件をもとにラプラス方程式を解いて得られた圧力分布に意味があるので、初期状態はその最終状態を得るための種を与えているにすぎません。
そうは言っても数値計算では、初期の形状は確認しておいた方が良いですよね。
【ポイント】
|
1 2 3 4 5 6 7 8 9 10 11 |
fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) ax.set_xlim(0, 2) ax.set_ylim(0, 1) ax.view_init(30, 225) ax.set_xlabel('$x$') ax.set_ylabel('$y$') ax.set_zlabel('$p$') |
【結果】
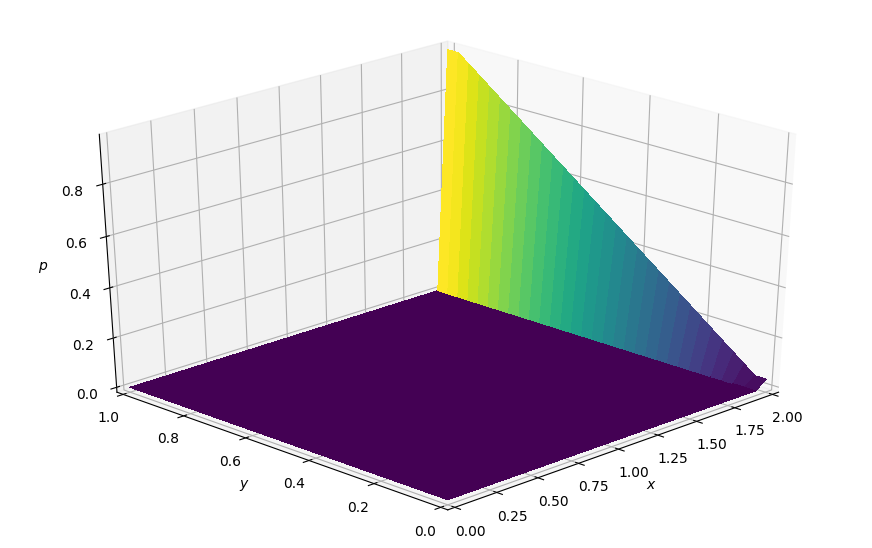


【ポイント】
コードを以下のように書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
l1norm_target = 1e-4 l1norm = 1 pn = np.empty_like(p) while l1norm > l1norm_target: pn = p.copy() p[1:-1, 1:-1] = ((dy**2 * (pn[1:-1, 2:] + pn[1:-1, 0:-2]) + dx**2 * (pn[2:, 1:-1] + pn[0:-2, 1:-1])) / (2 * (dx**2 + dy**2))) p[:, 0] = 0 # p = 0 @ x = 0 p[:, -1] = y # p = y @ x = 2 p[0, :] = p[1, :] # dp/dy = 0 @ y = 0 p[-1, :] = p[-2, :] # dp/dy = 0 @ y = 1 l1norm = (np.sum(np.abs(p[:]) - np.abs(pn[:])) /np.sum(np.abs(pn[:]))) |
これで最終状態の圧力のプロファイルが完成しています。
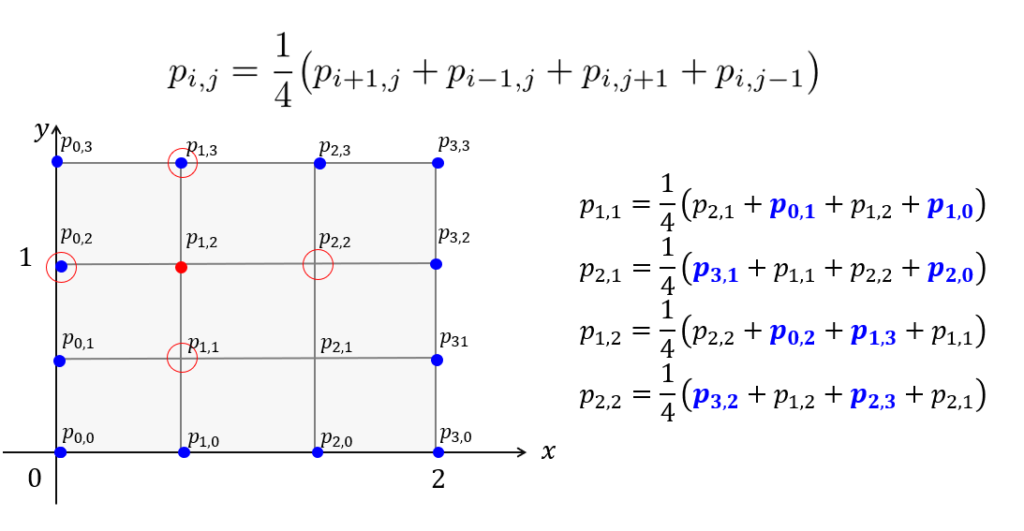
何を行っているのかを「4×4」の格子状の点で簡単にして、回折します。
p_{i,j}^n = \frac{1}{4}\big(p_{i+1,j}^n+p_{i-1,j}^n+p_{i,j+1}^n + p_{i,j-1}^n\big)\tag{15}
\end{align*}
ですから、例えば(1,1)の格子点上の圧力は上記のように以下のようになります。


青文字は境界条件で値が与えられているので、既知の値です。
これを見ればわかるように、(i,j)の格子点での圧力はその周りの圧力の平均値として計算しています。
これを全ての格子点上で行うことを考えます。


これで、未知の量について解くことができるのですが、
格子点数が多いとこのように行列計算で求めることは結構厳しいですよね。
この行列計算を行ってくれる方法としていろいろあるのですが、有名なのをいくつか挙げておきます。
- ガウス消去法(直接法)
- ガウス・ジョルダン法(直接法)
- ヤコビ法(反復法)
- ガウス・ザイデル法(反復法)
- SOR法(反復法)
などがあります。
詳しく勉強したい方は、以下の参考書がとてもわかりやすいです。
数値計算の闇について詳しく知りたい方は、☟こちらの参考書も合わせてお読みください。
その中でも今回は、反復法の中でも簡単な「ヤコビ法」で解くことにします。


収束判定は、
|
1 |
l1norm = (np.sum(np.abs(p[:]) - np.abs(pn[:])) /np.sum(np.abs(pn[:]))) |
としています。
全ての格子点上の値の合計と前のステップでの値の合計とを比較して、「1e-4(0.01%)」以下の誤差になれば収束したと判定しています。
では、次に収束した圧力分布を可視化してみてみましょう。
【ポイント】
コードを以下のように書きます。
|
1 2 3 4 5 6 7 8 9 10 11 |
fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) ax.set_xlim(0, 2) ax.set_ylim(0, 1) ax.view_init(30, 225) ax.set_xlabel('$x$') ax.set_ylabel('$y$') ax.set_zlabel('$p$') |
【結果】
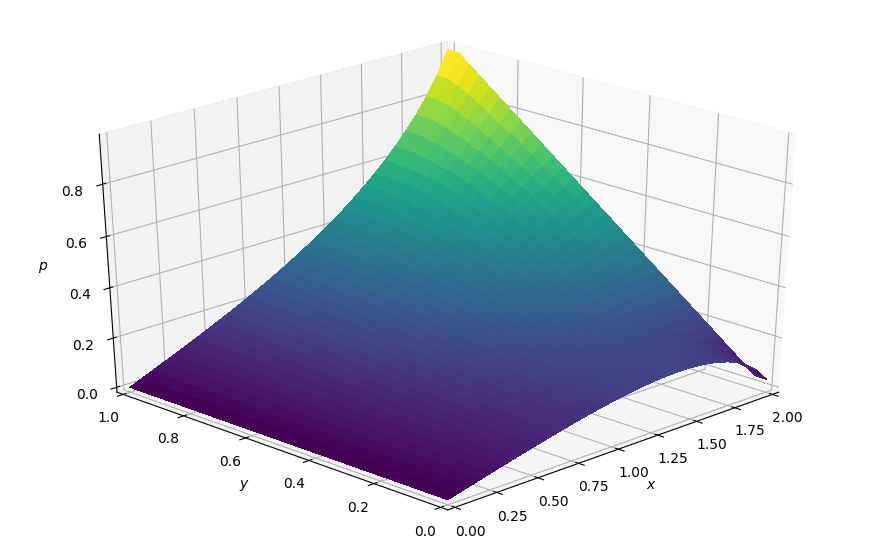


このような結果になりました(^^)/
関数にまとめる
今のままで良いのですが、関数にまとめてコードをきれいにまとめておきます。
☟初期状態を設定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import pyplot, cm from mpl_toolkits.mplot3d import Axes3D nx = 31 ny = 31 c = 1 dx = 2 / (nx - 1) dy = 2 / (ny - 1) ##initial conditions p = np.zeros((ny, nx)) # create a XxY vector of 0's ##plotting aids x = np.linspace(0, 2, nx) y = np.linspace(0, 1, ny) #境界条件 p[:, 0] = 0 # p = 0 @ x = 0 p[:, -1] = y # p = y @ x = 2 p[0, :] = p[1, :] # dp/dy = 0 @ y = 0 p[-1, :] = p[-2, :] # dp/dy = 0 @ y = 1 |
次にラプラス方程式を解く部分を関数にまとめます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
def laplace2d(p, y, dx, dy, l1norm_target): l1norm = 1 pn = np.empty_like(p) i=0 while l1norm > l1norm_target: pn = p.copy() p[1:-1, 1:-1] = ((dy**2 * (pn[1:-1, 2:] + pn[1:-1, 0:-2]) + dx**2 * (pn[2:, 1:-1] + pn[0:-2, 1:-1])) / (2 * (dx**2 + dy**2))) p[:, 0] = 0 # p = 0 @ x = 0 p[:, -1] = y # p = y @ x = 2 p[0, :] = p[1, :] # dp/dy = 0 @ y = 0 p[-1, :] = p[-2, :] # dp/dy = 0 @ y = 1 l1norm = (np.sum(np.abs(p[:]) - np.abs(pn[:])) /np.sum(np.abs(pn[:]))) i +=1 print(i) return p |
ラプラス方程式を解いた後に、「return p」でpを返す関数を作成しました。
次に、結果を可視化する関数を用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def plot2D(x, y, p): fig = plt.figure(figsize=(11, 7), dpi=100) ax = fig.gca(projection='3d') X, Y = np.meshgrid(x, y) surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,linewidth=0, antialiased=False) ax.set_xlim(0, 2) ax.set_ylim(0, 1) ax.view_init(30, 225) ax.set_xlabel('$x$') ax.set_ylabel('$y$') ax.set_zlabel('$p$') |
これで準備完成です(^^)/
初期の分布を見てみましょう。
|
1 |
plot2D(x, y, p) |
【結果】



これは境界条件だけを可視化したもので、特に意味があるものではありませんね。
このあと、ラプラス方程式を解くことによって意味のある分布になります。
|
1 |
p = laplace2d(p, y, dx, dy, 1e-4) |
これでラプラス方程式を解いたことになります。
いちおう収束のために何回ループしたのかも計算しておきました。
「1132回」収束のためにループ計算をしています。
では、最終状態の結果を見てみます。
|
1 |
plot2D(x, y, p) |
【結果】



まとめ
今回は、2次元のラプラス方程式をPythonで実装してみました。
本記事のシリーズを読むことでPythonを使ったナビエストークス方程式の実装まではいけると思いますので、是非最後までお付き合いくださいm(__)m
おすすめの書籍紹介
ネット上には無料で多くのことが学べるのですが、ネット情報だけだと情報が偏ったりします。
やっぱり書籍を手に取って体系だって学んだ方が良い場合も多いです。
初心者でもので体系だって学ぶことができる、且つあまり難しすぎない書籍をここで紹介しておきます。
Pythonの完全初心者は書籍で学ぶとよい
Python自体が不安だという方は、こちらの書籍から勉強しても良いかも知れません。
☟こちらの本がPython初心者が挫折することなく勉強できる本です。
(本記事のようのPython使用環境と異なりますが、とてもわかりやすいので全く問題ありません)
流体の勉強をしたい方
流体の数値計算以前に、流体力学を勉強しないと!!って思っている方は以下の参考書からはじめてみるのが良いと思います。
工学よりに書かれていて実用的な内容も触れながら、流体の理論的な内容も易しく書かれていますので大学1年生で偏微分を学んだ方にとってはちょうどよい参考書です。
数値流体の書籍
本記事で紹介している数値計算手法は、多くの数値解法のごく一部です。
特に、非線形方程式で記述できる流体現象のようなものは注意深く数値解法を選択しなくてはいけません。
以下の書籍は、値段が高いですが有限体積法をメインに数値解法がとても詳しく解説されています。