どうも(^^)/
流体力学の初投稿です♪
しかし、僕はあまり流体力学に長けていません(笑)
まずは基本的なことをまとめました。
非圧縮性流体の基礎方程式を示す。
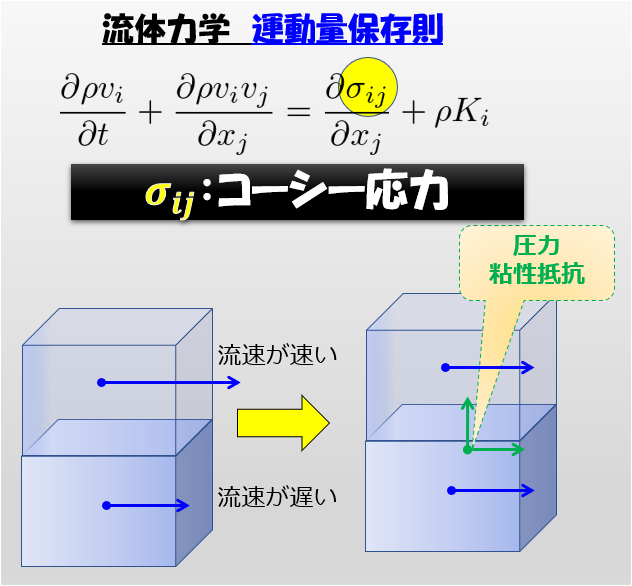
流体力学の基礎方程式(一般式)

※外力\(\bf{K}\)
流体力学の物理量(変数)は、「密度\(\rho\)、温度\(T\)、圧力\(P\)、速度\(v_{x},v_{y},v_{z}\)」の6変数です。
それに対して、式が
- 質量保存則⇒1つ
- 運動方程式⇒各方向あるので3つ
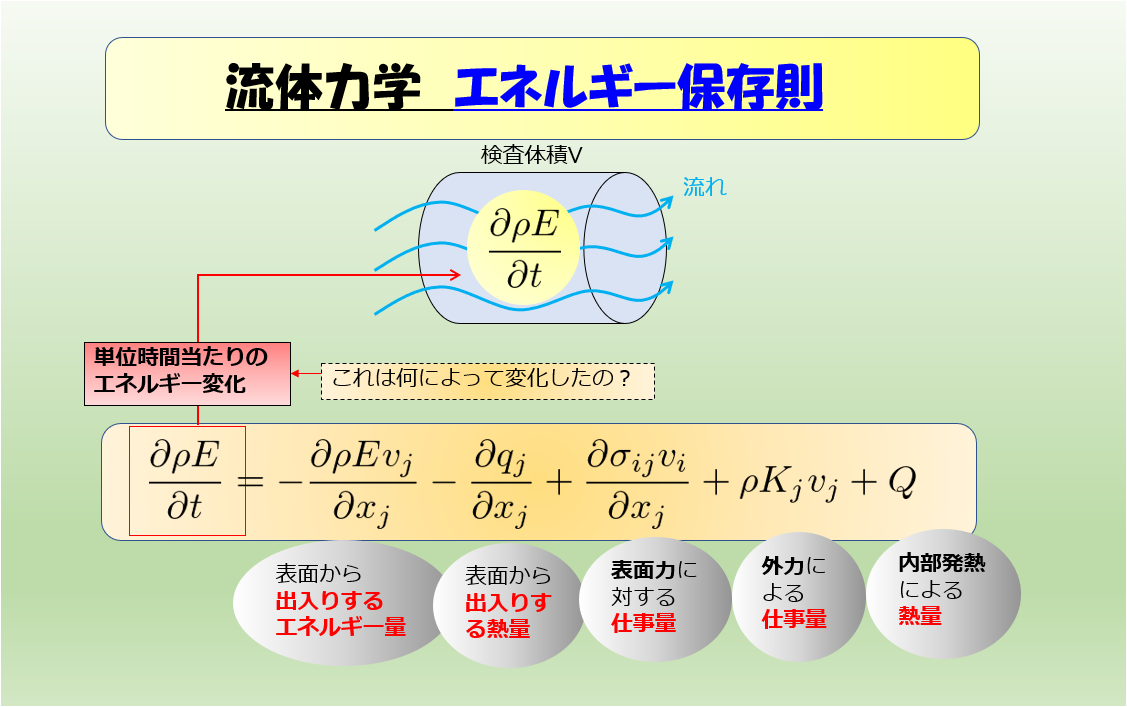
- エネルギー保存則⇒1つ
- 理想気体の状態方程式⇒1つ
このように合計6個の式があります。
変数6つに式が6つなので原理的には解けることになります。
※しかし、運動方程式はとても複雑な速度に対して非線形であり、一般解が見つかっておりません。
ゆえに、手計算で解を求めることができず、ある条件を設けて近似的な解を求めるか、式を離散化して数値解析で求めるかのいずれかになります。
まずは圧縮性流体、非圧縮性流体について簡単に説明したいと思います。
圧縮性流体とは
密度変化が大きくなる主な原因としては以下が上げられます
1.圧力変化
2.温度変化
3.組成変化
圧力、温度変化による密度変化が小さい場合は、非圧縮性流体として扱ても良い精度で解析ができます。
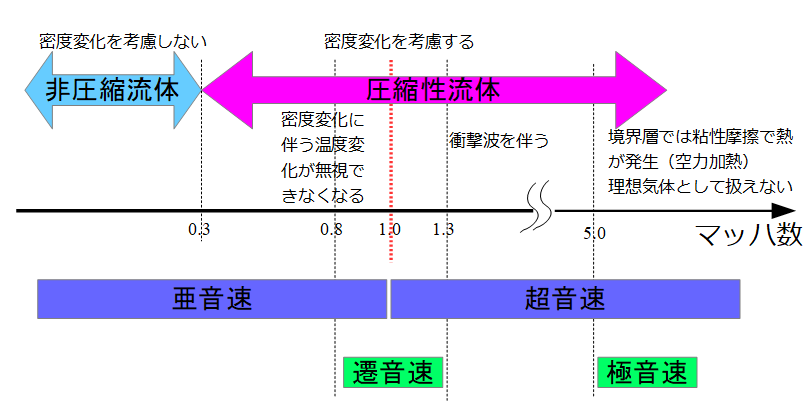
密度変化が大きい場合は、解析領域内で「大きな温度差がある場合」、「流速が音速に近づく場合」に顕著になります。
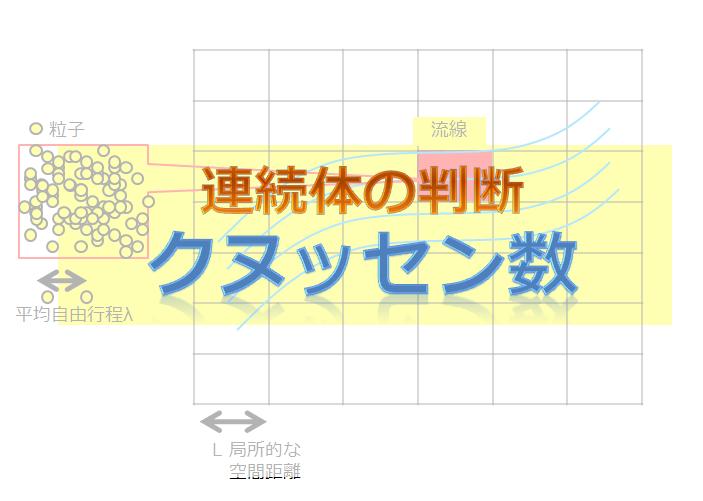
マッハ数\(M=\frac{u}{a}\)が、\(M>0.3\)の時、圧縮性流体として扱うことを推奨されています。
※\(a\)は音速
このような高速な流れ場では、圧力が局所的に急変する衝撃波が形成されますので、衝撃波を考慮した解析が必要になります。
マッハ数\(0.8<M<1.2\)
亜音速
亜音速流れにおいて、流入部の圧力は下流部の圧力の結果として、計算上求まります。
ですので、流入境界条件として、「速度3成分、温度」の4成分すべてを設定し、流出部に「圧力」を設定するのが一般的です。
マッハ数\(1.2<M<3.0\)
超音速
超音速流れにおいて、圧力の影響は下流方向のみ伝搬されます。
ですので、流入境界条件として「速度3成分、圧力、温度」の5成分すべてを設定する必要があります。
流出部には、ひとつも設定する必要はないということになります。
圧縮性解析手法には2つの手法があるので下記に示しておきます。
1.圧力ベースソルバー(亜音速から遷音速流れ)
2.密度ベースソルバー(遷音速から超音速流れ)
非圧縮性流体での基礎方程式に変更
非圧縮性流体つまり縮まない流体(密度\(\rho\)が一定)に対しては基礎方程式がもう少しシンプルになります。
密度が一定とは、何に対して一定か?
これをはっきりさせないといけませんね。
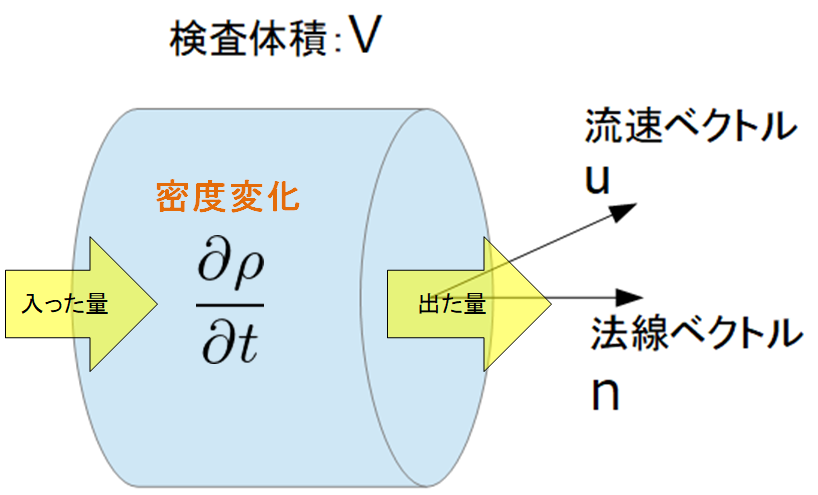
これは質量保存則を見ればわかります。
質量保存則の変更

上記のように密度は、流体の流れに沿って一定というのが非圧縮性流体への扱いです。
つまり、上記のように物質微分が0を意味しています。
何も難しいことはありません。下記の計算をしたらイメージがつきます。
流れに沿って密度が変化がないとは以下のように記述できます。
\rho(v_{x}+\delta v_{x},v_{y}+\delta v_{y},v_{z}+\delta v_{z},t+\delta t)-\rho(v_{x},v_{y},v_{z},t)=0\end{align*}
そして、第一項をテーラー展開して\(\delta v_{x}\),\(\delta v_{y}\),\(\delta v_{z}\),\(\delta t\)の2次の項以降を無視します。
各自計算をしてみましょう(^^)/
結果は↓
となりますので、∇演算子を用いて第二項を整理すると、
運動方程式の変更
非圧縮性流体についての運動方程式は、先ほどの「非圧縮性仮定による質量保存から得た\(\nabla \cdot \boldsymbol{v}=0\)」を用いれが導出できます。

エネルギー保存則の変更
エネルギーの保存則と書いていますが、非圧縮性の場合は温度が速度場に乗って変化する「温度場の輸送方程式」を解くことになります。
下記のような感じです。

まとめ:非圧縮性流体の基礎方程式
非圧縮性流体の基礎式をまとめておきます。

※外力\(\bf{K}\)、粘性係数\(\mu\)
流体力学の物理量は、「密度\(\rho\)、温度\(T\)、圧力\(P\)、速度\(v_{x},v_{y},v_{z}\)」ですが6変数ですが、密度が\(\rho=const\)と一定扱いなので、変数は5変数です。
それに対して、式が
- 質量保存則⇒1つ
- 運動方程式⇒各方向あるので3つ
- エネルギー保存則⇒1つ
このように合計5個の式があります。
ですので、原理的にはこの方程式は解けることになります。
しかし、元の基礎方程式と異なる部分は非圧縮性流体のとして取り扱った場合、
「質量保存則」「運動方程式」で圧力と速度が求まってしまうため、エネルギー則を解く必要がないということです。
温度場が知りたい場合は、別個で速度に沿った温度場(温度の輸送方程式)として解いてやれば良いということですので、速度と圧力だけを知りたい場合は計算の負荷は一気に下がります。
非圧縮性流体として現象を取り扱うものとして、CAE解析を行う際、「あれ?温度は解かなくてもいいの?」って思ったことがあるかもしれませんが、上述の理由からなのですよね。
非圧縮性流体は存在するのか?
非圧縮性流体とは、圧力をかけても縮まない流体ということです。
しかし、流体は実際は圧力とかけると、それが水だろうが空気だろうが、液体だろうが気体だろうが縮むものです。
音速と比較して、流れが十分遅ければ、数学的な取り扱いとして非圧縮(縮まないもの)として扱っても実現象を十分な精度で表すことができるかどうかを言っているだけですね。
×水=非圧縮性
×空気=圧縮性
と、このように解釈してはいけません。
水だって圧縮性を考慮しないと実現象を再現できない場合は存在します。
つまり、非圧縮性か圧縮性かは、流れの状態による数学的な取り扱いを区別しているものであることに注意しましょう!